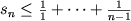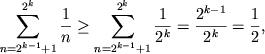Wetenschapsquiz

quote:

Op maandag 12 december 2005 16:55 schreef thabit het volgende:
Dit zijn de antwoorden die ik heb ingestuurd. Ik heb er een paar gegokt, dus ik verwacht niet dat ze allemaal goed zijn. Maar wie weet zit er een kansje in.
1C 2A 3A 4A 5C 6A 7A 8B 9C 10B 11B 12B 13A 14B 15C 16C 17C 18B 19A 20C

quote:

Op maandag 12 december 2005 17:02 schreef Quarks het volgende:

[..]

Kun je 15 uitleggen?

Ik dacht dat het ruikende deel van je neus vrij hoog in je neusholte zit.

quote:

Op maandag 12 december 2005 17:38 schreef thabit het volgende:
Ik had op internet iets gevonden wat vrij vaag was, maar wel het meest op C lijkt. Grofweg kwam het erop neer dat je door te snuffelen bepaalde reukcentra in de hersenen actief maakt. Het was onderzoek gedaan in Berkeley, dus wel vrij serieus te nemen.

quote:

Tijdens de normale ademhaling bereikt de inademingslucht de bovenste neusgang, waar het reukepitheel zich bevindt. De daar aangekomen lucht is door het bloed en vochtrijke neusslijmvlies voorverwarmd, vochtig gemaakt en van veel stofdeeltjes gezuiverd. Als men beter wil ruiken, gaat men snuffelen, waardoor de dan snel in- en uitgeademde lucht de bovenste neusgang beter kan bereiken. Door het snel op elkaar volgen van reukprikkels wordt de geurgewaarwording versterkt. Het reukzintuig kan ook worden gestimuleerd via de tongbewegingen, waarbij de lucht uit de mond via de achterzijde (neuskeelholte) omhoog wordt gestuwd naar het reukepitheel. De `smaak’ van het voedsel berust voor een belangrijk deel op geurgewaarwordingen die op deze wijze tot stand komen; bij verlies van de reuk is de smaak sterk verminderd. Het aantal door de mens waar te nemen geuren wordt geschat op 200.000.

quote:

Op maandag 12 december 2005 18:20 schreef thabit het volgende:

[..]

Ah, maar waarom doen we dan korte ademteugjes bij het snuffelen in plaats van 1 lange stevige?

quote:

Op dinsdag 29 november 2005 18:31 schreef Quarks het volgende:

[..]

Je kunt het zwaartepunt beïnvloeden met je tegels.
Door meer tegels als contragewicht te gebruiken verleg je je zwaartepunt.

[afbeelding]

Uitleg:

We noemen de bovenste tegel T1, en de tegel daaronder T2, enzovoorts. We laten de toren naar rechts overhellen.

Hoeveel kan T1 uitsteken t.o.v. T2 zodat T1 precies in evenwicht hangt?
We noemen de breedte van de tegel d. Het gedeelte wat T1 links uitsteekt t.o.v. van zijn draaipunt op T2 noemen we X1. Het gedeelte wat T1 rechts uitsteekt t.o.v. zijn draaipunt op T2 noemen we d-X1. De massa van de tegel doet niet terzake en laten we dus weg. Ook de zwaartekrachtversnelling laten we weg omdat die niet van invloed is behalve dat hij in werkelijkheid aanwezig moet zijn.

De Momenten links en rechts van het draaipunt (dat op d-X1 ligt) moeten gelijk zijn. Omdat de tegel een homogene massa is die niet dikker of dunner naarmate je meer naar buiten of binnen komt, kunnen we alle massa veronderstellen aanwezig te zijn in het punt 0,5 d respectievelijk 0,5 (d-X1).

Het Moment links wordt daarmee: 0,5 x X1. Het Moment rechts wordt zo 0,5 (d-X1). De Momenten zijn gelijk omdat de zaak in evenwicht hangt, waaruit volgt X1 = 0,5 d. Tegel T1 steekt X1-d uit, dus T1 steekt 1/2 tegel uit t.o.v. de onderliggende tegel T2.

Hoeveel kan T2 uitsteken t.o.v. T3 zodat T2 precies in evenwicht hangt (met T1 nog aanwezig)?
Ook hier geldt weer dat de Momenten links en rechts van het draaipunt, dat op d-X2 ligt, gelijk moeten zijn.

Het Moment links van het draaipunt: 0,5 x X2. Het Moment rechts van het draaipunt bestaat nu evenwel uit twee componenten, te weten voortvloeiend uit T2 én voortvloeiend uit T1. Beiden moeten bij elkaar worden opgeteld en gelijk zijn aan het Moment links. De eerste component is 0,5 x (d-X2). De tweede component, namelijk de bijdrage van T1, is: 0,5 x (d-X2). Omdat T1 precies in evenwicht ligt mag alle massa worden verondersteld in één punt te liggen, nl. het draaipunt van T1 op T2.

Links en rechts zijn gelijk dus 0,5 x X2 = 0,5 x (d-X2) + (d-X2). Oftewel 4 X2 = 3 d, en X2 = 0,75 d. Tegel T2 steekt dus 1/4 tegel uit t.o.v. de onderliggende tegel T3.

Totaal steekt de toren nu uit 1/2 + 1/4 = 0,75 tegel.

Hoeveel kan T3 uitsteken t.o.v. T4 zodat T3 precies in evenwicht hangt (met T1 en T2 nog aanwezig)?
Er geldt weer hetzelfde als boven, echter nu liggen er twee tegels bovenop waarvan het zwaartepunt mag worden geacht te liggen in d-X3. De zaak ligt immers in evenwicht.

De vergelijking wordt hiermee 0,5 x X3 = 0,5 x (d-X3) + 2 x (d-X3). Oftewel X3 = d � X3 + 4 d � 4 X3, hetgeen oplevert 6 X3 = 5 d, dus X3 = 5/6 d. Tegel T3 steekt dus 1/6 tegel uit t.o.v. de onderliggende tegel T4.

De toren steekt nu uit 1/2 + 1/4 + 1/6 = 0,91 tegel.

Hoeveel kan T4 uitsteken t.o.v. T5 zodat T4 precies in evenwicht hangt (met T1, T2, en T3 nog aanwezig)?
0,5 x X4 = 0,5 x (d-X4) + 3 x (d-X4) hetgeen oplevert 8 X4 = 7 d, dus X4 = 7/8 d. Tegel T4 steekt dus 1/8 tegel uit t.o.v. de onderliggende tegel T5.

De toren steekt nu uit 1/2 + 1/4 + 1/6 + 1/8 = 1,04 tegel.

Hoeveel kan T5 uitsteken t.o.v. T6 zodat T5 precies in evenwicht hangt (met T1, T2, T3, en T4 nog aanwezig)?
0,5 x X5 = 0,5 x (d-X5) + 4 x (d-X5) hetgeen oplevert X5 = 9/10 d. Tegel T5 steekt dus 1/10 tegel uit t.o.v. de onderliggende tegel T6.

De toren steekt nu uit 1/2 + 1/4 + 1/6 + 1/8 + 1/10 = 1,14 tegel.

Deze reeks loopt natuurlijk gewoon door. Tegel 11 overschrijdt de 1,5 en tegel 31 overschrijdt de 2. Bij tegel 1000 zit je al op 3,7427. Bij tegel 5000 zit je op de 5,7432.

quote:

Op maandag 12 december 2005 19:47 schreef thabit het volgende:
Er zijn er een aantal die ik 100% zeker weet en een daarvan is dat die toren met tegels toch echt oneindig (of eigenlijk beter geformuleerd: willekeurig) ver kan.

quote:

Op dinsdag 13 december 2005 00:45 schreef Jegorex het volgende:

[..]

En ik weet 100% zeker dat het niet oneindig ver opzij kan gaan.
De toren (of een deel ervan) zal op den duur niet meer in evenwicht staan en omvallen.

quote:

Op dinsdag 13 december 2005 00:58 schreef Koekepan het volgende:
De vraag is nu: gegeven een overhang van x, wat is het minimale aantal N(x) aan tegels dat ik nodig heb om x te bereiken. Komen we daar de harmonische reeks weer tegen, of is er een betere strategie? Gelieve geen onzin te antwoorden op deze vraag. M.a.w.: graag alleen reacties van thabit.

quote:

Op dinsdag 13 december 2005 12:10 schreef thabit het volgende:
De harmonische reeks levert uiteraard het beste resultaat.

Stel dat de tegels lengte 2 hebben, en hanteer als conventie dat de stapel nog altijd stabiel is als de rand van elke tegel recht onder het zwaartepunt van de deelstapel erboven zit. Mocht je deze eis willen laten vallen, dan kun je natuurlijk elke uitwijking krijgen die een epsilon minder is dan die van de harmonische reeks.

Stel dat het zwaartepunt van de bovenste steen op positie 0 zit, en dat we vanaf de bovenste steen in de positieve richting willen werken. Laat s_n gedefinieerd zijn als de positie van het zwaartepunt van de n'de tegel.

Te bewijzen: s₁+...+s_n<=1+1/2+...+1/(n-1).

We gebruiken nu volledige inductie naar n. Het geval n=1 is triviaal. Stel nu dat het geldt voor de bovenste n stenen. Waar zit het zwaartepunt van deze stenen?
Welnu, dat zit op positie
[afbeelding]
Omdat we de tegel eronder hooguit een afstand 1 verder kunnen krijgen dan dit zwaartepunt, geldt dat s_n+1<= 1/1+...+1/n, hetgeen we moesten bewijzen.

De harmonische reeks geeft gelijkheid in de geLaTeXde afschatting en dit laat zien dat daar de stapel ook stabiel is.

quote:

Op dinsdag 13 december 2005 12:16 schreef Quarks het volgende:

[..]

Deze reeks is dus niet eindig.
Dat wil zeggen, het verschil tussen 1000 en 1001 tegels maakt natuurlijk erg weinig uit voor de overhang van de bovenste tegel, maar toch blijft met de hoogte de maximale overhang toenemen.

quote:

Op dinsdag 13 december 2005 12:16 schreef Quarks het volgende:

[..]

Dat dacht ik ook ja:

Harmonische reeks: 1 + 1/2 + 1/3 + 1/4 + 1/5 .... 1/n
Een harmonisch getal Hn is deze reeks tot stap n herhaald.
Dus harmonisch getal 5 = 1 + 1/2 + 1/3 + 1/4 + 1/5.

De maximale overhang voor een stapel van n tegels blijkt te zijn:
Hn / 2.

Voor 5 tegels is de maximale overhang 1,142
Voor 30 tegels is dat 1.997
Voor 100 tegels is dat 2.59
Voor 1000 tegels 3,74.

Deze reeks is dus niet eindig.
Dat wil zeggen, het verschil tussen 1000 en 1001 tegels maakt natuurlijk erg weinig uit voor de overhang van de bovenste tegel, maar toch blijft met de hoogte de maximale overhang toenemen.

quote:

Op dinsdag 13 december 2005 12:20 schreef thabit het volgende:

[..]

Deze manier van redeneren is natuurlijk onjuist. Er zijn zat reeksen die het beschreven eindige gedrag hebben voor de waarden 5, 30, 100 en 1000 en toch niet divergeren.

quote:

Op dinsdag 13 december 2005 12:23 schreef Koekepan het volgende:

[..]

Had ik nou niet iets gezegd over onzinnige bijdragen? Dit is echt pijnlijk om te lezen voor iedereen met een béétje wiskundig besef.

quote:

Op dinsdag 13 december 2005 12:32 schreef Doderok het volgende:

[..]

Mensen, mensen... vertel me liever hoe het met de eenden zit

quote:

Op vrijdag 16 december 2005 13:54 schreef yoppybt het volgende:
Iedereen zegt 10->B (de trampoline, springveren moet je in je rugzak stoppen).

Wat echter als de trampoline superstrak gespannen is (zodat hij zo goed als niet veert)? Dan ben je toch echt beter af met verende schoenen.

10->B en 10->C is dus in ieder geval een fout antwoord bij een superstrakke trampoline.

Bij een meer verende trampoline ligt het misschien anders maar waar ligt dan het kantelpunt?

De vraag doet verder geen enkele uitspraak over de veerkracht van de trampoline of de schoenen dus blijft alleen antwoord A over.

quote:

Op dinsdag 20 december 2005 18:09 schreef yoppybt het volgende:
Ik heb het niet over het ideale geval (perfecte vering van de trampoline) maar over het andere uiterste: geen vering van de trampoline.
Stel dat hij zonder trampoline springt, gewoon op de grond. Dan bieden de veren onder de schoenen zeker wel een voordeel. Een strak gespannen trampoline gedraagt zich als de grond. Een normaal gespannen trampoline veert mee.
Hoe strak moet volgens jou de trampoline gespannen zijn opdat de veren onder de schoenen geen voordeel opleveren?

quote:

Op woensdag 21 december 2005 00:03 schreef Gia het volgende:
In het discussieforum van de NWQ kwam ik het volgende tegen bij de vraag over de wijnvlek:

[afbeelding]

Heb het geprint en de twee vakjes uitgeknipt. Ze zijn precies even donker.
Verder heb ik ook wel wat wijnvlekken op onze mexicaans eiken salontafel, als ik die daaruit zou kunnen knippen, weet ik vrijwel zeker dat de vlek overal even donker is.

(Ja, ik weet dat ik niet meer in kan zenden, maar vind het alsnog leuk om de antwoorden te zoeken voor zaterdag.)

quote:

Op woensdag 21 december 2005 01:42 schreef Doderok het volgende:

[..]

Net op tijd (min of meer) aan dit topic gedacht toen ik enkele wijnvlekken wou wegvegen:
[afbeelding]
Rechts een vlek, links een gefotoshopt vlak van egale kleur.
Op het hout is plastic aangebracht, mogelijk dat daardoor enkel een rand overbleef.
In ieder geval is duidelijk dat men bij een egaal gekleurde vlek de randen niet automatisch als donkerder ziet. (de wereld zou er raar uitzien)

quote:

1) Wanneer verdwijnt aarde aan horizon?

C, helemaal niet. De maan keert altijd dezelfde kant naar de aarde toe. Daarom zien wij alleen de voorkant van de maan en nooit de achterkant. Sta je op de maan met de aarde pal boven je, dan sta je op de maan-evenaar. Je staat op het 'midden' van de zichtbare maanschijf en de aarde blijft altijd boven je hoofd staan. Overigens schommelt de maan wel een klein beetje, maar deze zogeheten libraties zijn te klein om de aarde op de horizon te krijgen. Antwoorden a en b waren instinkers. De zon staat 12 uur boven de horizon voor een waarnemer op de aardse evenaar. Daar heeft de maan niets mee te maken. En de maan draait in 27 dagen, 7 uur en 43 minuten rond zijn as en rond de aarde.
Geraadpleegde expert: Govert Schilling, wetenschapsjournalist, gespecialiseerd in sterrenkunde.

2) Hoe lang wachten op trein van 3x per uur?

A, meer dan 10 minuten. Als alle tussenpozen precies 20 minuten zouden zijn geweest, dan zouden alle wachttijden tussen 0 en 20 minuten even waarschijnlijk zijn geweest en dan zou je gemiddeld precies 10 minuten hebben moeten wachten. Maar nu niet alle tussenpozen 20 minuten zijn, is de crux dat je een grotere kans hebt te arriveren in een lange tussenpoos dan in een korte. Daardoor wordt de gemiddelde wachttijd meer dan 10 minuten. De formule die bij de oplossing hoort, luidt als volgt: gemiddelde wachttijd = (a^2 + b^2 + c^2)/120. De tussenpozen tussen de vertrektijden zijn a, b en c, waarbij a + b + c = 60. Een getallenvoorbeeld: Stel de trein rijdt om 12.00 uur, 12.10 uur en 12.30 uur en weer om 13.00 uur. Invullen in de formule levert: gemiddelde wachttijd = (10 x 10 + 20 x 20 + 30 x 30)/120 = 11,7 minuten.
Geraadpleegde experts: prof. dr. Lex Schrijver, onderzoeker bij het Centrum voor Wiskunde en Informatica en hoogleraar wiskunde aan de Universiteit van Amsterdam (UvA), prof. dr. Chris Klaassen, hoogleraar statistiek aan de UvA en dr. Chris Zaal, wiskundige aan de UvA.

3) Hoe hoog komt gekerfd hartje?

A, twee meter. De cellen die zorgen voor de lengtegroei van een boom zitten helemaal in de top. Jonge cellen worden daar naar beneden toe afgezet. Als deze cellen gaan strekken, 'duwen' ze als het ware de groeipunt een beetje de hoogte in. Zulke groeipunten zitten ook aan de uiteinden van takken en twijgen. En hoe bomen dan dikker worden? Rondom de stam, net onder de bast, zitten ook cellen die zich delen. Die zetten naar binnen toe houtcellen af. Daardoor worden de groeizone en de bast naar buiten gedrukt en neemt de omtrek van de boom toe. De schors gaat scheuren en schilfert langzaam af.
Geraadpleegde expert: dr. Hendrik Poorter, plantenfysioloog aan de Universiteit Utrecht.

4) Wat gebeurt met ijsblok plus kuiltje water in magnetron?

A, het water wordt heet en het ijs blijft ijs. Een magnetron is zo gemaakt dat hij heel goed vloeibaar water verhit. Dat komt doordat de moleculen heen en weer gaan wiebelen in het elektromagnetische veld van de magnetronstraling. Hoe harder moleculen bewegen, hoe warmer het is. IJs neemt duizend tot tienduizend keer minder goed warmte op dan water. Dat komt omdat bij ijs de watermoleculen in een keurslijf zitten. In vaktaal: om te verwarmen moeten de dipolen kunnen relaxeren. Daarvoor is rotatie nodig en die rotatie is er bijna niet in vaste toestand.
Geraadpleegde expert: prof. dr. Jo Hermans, hoogleraar natuurkunde aan de Universiteit Leiden.

5) Waarom lopen pinguïns gek?

Bij deze vraag is wat misgegaan tijdens een herschrijfronde. Deze vraag telt niet mee voor de prijzen. Pinguïns waggelen omdat het de minste energie kost. Dat antwoord stond er niet bij. Er is geen meest juiste antwoord dat er wel bijstaat. Goed, energie dus. Door te waggelen kunnen pinguïns tachtig procent van de energie die nodig is om een pas te zetten, weer in de spieren opnemen voor de volgende pas. Ter vergelijking: mensen halen met lopen maar zeventig procent. Je ziet pinguïns soms ook over ijsbrokken hoppen met twee poten tegelijk of zelfs over hun buik over het ijs te glijden. Dat spaart nog meer energie, maar dat kan lang niet altijd. Pinguïns hebben overigens weldegelijk knieën. De knieën van pinguïns zitten, net als een groot deel van hun poten, verborgen onder hun verenpak.

6) Kun je een fata morgana fotograferen?

A, ja zonder probleem. Een fata morgana is een luchtspiegeling. En een luchtspiegeling bestaat echt. Het is dus niet iets dat onze ogen of hersenen verzinnen. Je kunt hem gewoon fotograferen.
Geraadpleegde expert: prof. dr. Lucas van Vliet, hoogleraar natuurkunde aan de Technische Universiteit Delft.

7) Kan water branden?

C, nee. Water kan niet branden omdat het in een mengsel van zuurstof met waterstof het meest stabiele eindproduct vormt. Waterstof met zuurstof kan waterstofperoxide als minder stabiel intermediair vormen. Maar dit ontleedt bij hogere temperatuur weer in water en zuurstof. Als je waterstof toevoegt aan waterstofperoxide, verbrandt de uit het waterstofperoxide vrijgekomen zuurstof tot... water! Dit is een onomkeerbaar proces. Bij extreem hoge temperatuur ontleedt water in zuurstof en waterstof. Zelfs dan zal geen verbranding optreden. Dat komt doordat de concentraties van waterstof, zuurstof en water in evenwicht zijn.
Geraadpleegde expert: prof. dr. Rutger van Santen, hoogleraar scheikunde aan de Technische Universiteit Eindhoven.

8) Waarom lijken pausen op elkaar in oude boeken?

B, illustratoren gebruikten voor elke geestelijke dezelfde houtsnede. Het maken van houtsneden was een intensief werk. Illustratoren gebruikten oude houtsneden en pasten die aan. Zo maakten ze van een paus een bisschop door bij de paus de tiara te vervangen door een bisschopsmijter. Natuurlijk zullen de illustratoren soms best gegokt hebben, maar dat is niet de belangrijkste reden.
Geraadpleegde expert: dr. Karin Tilmans, historica aan de Universiteit van Amsterdam.

9) Hoe zie je een regenboog vanuit een parachute?

C, als een cirkel. Als je de boog vanaf een hoogte bekijkt, zie je een cirkel. Een regenboog ontstaat als de zon op druppels schijnt. De druppels veranderen het zonlicht van richting en rafelen het uiteen in verschillende kleuren. We zien een boog gewoonlijk als boog en niet als cirkel omdat vanaf de grond bekeken het aardoppervlak in de weg zit. De grootste bogen zijn 's ochtends vroeg of 's avonds laat te zien. De kleinste bogen heb je midden op een zomerse middag. Dan is er namelijk geen boog, omdat de zon te hoog staat en de hele regenboog onder de horizon verdwenen is.
Geraadpleegde expert: drs. Kees Floor, meteoroloog en wetenschapsjournalist.

10) Spring je hoger trampoline met of zonder springstelten?

B, je springt het hoogst zonder springstelten, dus met de stelten in een rugzak. Dat komt doordat het afzetten op een 'zachte' ondergrond minder goed gaat dan op een hardere. Door het toevoegen van springveren wordt de combinatie trampoline plus springveren aanmerkelijk zachter. In vaktaal: de veerconstante van twee veren in serie is altijd kleiner dan die van één van de twee apart. Overigens, als de springer zich van grote hoogte van de trampoline zou laten terugveren, speelt de afzet maar een kleine rol en zou het weinig uitmaken. Dan zou antwoord C goed zijn. In dat geval zou de val-energie verdeeld worden over de twee veermechanismen. De springer zou tot bijna de oorspronkelijke hoogte terugveren, gesteld dat de elasticiteit van beide bijna perfect is.
Geraadpleegde experts: dr. Rinke Wijngaarden, natuurkundige aan de Vrije Universiteit Amsterdam en prof. dr. Jo Hermans, hoogleraar natuurkunde aan de Universiteit Leiden.

11) Heeft een melktand een wortel?

B, ja maar bij het wisselen drukt de nieuwe tand de oude weg. Wanneer de blijvende tand, die onder de melktand in een tandzakje in het bot ligt, gaat groeien, verdwijnt het laagje bot tussen de melktand en de blijvende tand door de druk. Vervolgens verdwijnt de wortel van de melktand. Wanneer de hele wortel van de melktand door het lichaam is opgenomen, blijft de kroon van de tand nog enige tijd op zijn plaats in de kaak door de hechting aan het tandvlees en de verbinding van zenuwweefsel met onderliggend weefsel. Uiteindelijk groeit de nieuwe tand zover omhoog dat de kroon van de melktand losscheurt van het tandvlees.
Geraadpleegde expert: Dien Gambon, kindertandarts bij Bambodino in Rotterdam.

12) Wat gebeurt met bezemsteel op uitgestoken vingers?

B, de bezemsteel steunt beurtelings op de ene en de andere vinger, tot die elkaar raken. De bezemsteel blijft liggen op de vinger die het dichtst bij het zwaartepunt ligt, omdat daar de wrijving het grootst is. De andere vinger ondervindt minder wrijving, waardoor de bezemsteel over die vinger heen schuift. Deze andere vinger komt daardoor steeds dichter bij het zwaartepunt te liggen, waardoor de wrijving toeneemt. Als de wrijving op deze vinger groter is dan die op de eerste vinger, glijdt de eerste vinger naar het zwaartepunt. De vingers wisselen elkaar bij deze beweging af, tot ze tegen elkaar aan liggen. Het zwaartepunt van de bezemsteel rust dan op de vingers en de bezemsteel balanceert.
Geraadpleegde expert: drs. Paul Vlaanderen, natuurkundige aan de Universiteit van Amsterdam.

13) Heeft moedereend een grotere boeggolf dan het kuiken?

C, er is geen verschil. Als je een steen in een vijver gooit, breiden de golven zich in kringen uit. Net als een steen wekt een eend (of een schip, dat maakt niet uit) in alle richtingen continu golven op. Bij de voorkant van de eend zijn de cirkels nog klein. Verder terug langs de route die hij heeft afgelegd, zijn ze groter. Als je vanaf de boeg een lijn trekt langs die cirkels, krijg je een lange V waarvan de punt altijd 39 graden (2x19,5 graden) meet. Hoe sneller de eend zwemt, des te sneller de golfcirkels zich uitbreiden. Daarom is de hoek van de boeggolf altijd hetzelfde, ongeacht of die veroorzaakt wordt door een grote eend, een kleine eend of een speedboot.
Geraadpleegde expert: dr. ir. Hoyte C. Raven, Maritiem Research Instituut Nederland, Wageningen.

14) Waardoor is een wijnvlek in het centrum lichter?

B, bij het opdrogen trekken de gekleurde deeltjes naar de randen. Rode wijn bestaat grotendeels uit water. De gemorste plas vormt een natte plek onder invloed van adhesie, cohesie en de zwaartekracht. Als het water verdampt, vliegen de watermoleculen de lucht in. De verdamping vindt voornamelijk langs de rand van de plas plaats, omdat moleculen uit het centrum veel hinder ondervinden van de damp boven de plas. Onder ideale omstandigheden zou de plas zich samentrekken als water aan de randen verdampt. Het tafelblad is echter verre van ideaal. Het bevat minuscule onregelmatigheden die zorgen dat de plas zich niet samentrekt. Voor de liefhebber: de onregelmatigheden zorgen dat iedere gewenste contacthoek tussen wijn en oppervlak mogelijk is. Goed, omdat er een tekort is ontstaan aan water aan de rand van de plas, vloeit water samen met opgeloste deeltjes vanuit het midden van de plas naar de buitenkant. Dat gaat zo door totdat de plas geheel verdampt is. De meeste gekleurde deeltjes komen dus uiteindelijk aan de rand terecht en vormen zo een ringvormige vlek.
Geraadpleegde experts: prof. dr. Lucas van Vliet en prof. dr. Ted Young, hoogleraren natuurkunde aan de Technische Universiteit Delft.

15) Hoe komt het dat we beter ruiken als we snuffelen?

B, snuffelen veroorzaakt wervelingen die zorgen dat de geur hoog in de neusholte dringt. Bij het inademen zijn de luchtstromen door de neus anders als je gewoon inademt of snuffelt. De neusholte bevat schotjes en is aërodynamisch zo gebouwd dat de meeste lucht bij gewoon ademen niet langs het reukepitheel stroomt. Het snuffelen veroorzaakt extra wervelingen in de lucht die beter tot hoger gelegen receptoren doordringen.
Geraadpleegde expert: dr. ir. Marien de Bruyne, neurobioloog aan de Vrije Universiteit van Berlijn.

16) Waarom wel last van scheve foto, maar niet van scheef hoofd?

C, onze hersenen corrigeren het gedraaide beeld. Dat gaat met behulp van informatie uit verschillende organen. Via de otholieten, kleine stukjes bot op de tasthaartjes in ons evenwichtsorgaan, registreren de hersenen waar naartoe ons hoofd beweegt en in welke stand het staat. Gegevens over de spierspanning en de spierpositie in de nek leveren extra informatie. En halfcirkelvormige kanalen in het evenwichtsorganen detecteren bewegingen in meerdere richtingen. Antwoord A is fout. Ook van een staafje of een lijntje, geplaatst tegen een uniforme achtergrond, kunnen we de oriëntatie aangeven. Uit experimenten is gebleken dat we daarbij slechts kleine systematische fouten maken. Antwoord B is fout, omdat onze ogen slechts een graad of vijf om hun kijk-as kunnen draaien.
Geraadpleegde expert: prof. dr. Casper Erkelens, hoogleraar fysica van de mens, Universiteit Utrecht.

17) Hoe ver kan een stoeptegeltoren uitsteken?

C, oneindig ver. Het handigst gaat het als je van bovenaf rekent en bouwt. Het zwaartepunt van de bovenste tegel mag niet buiten de tegel eronder vallen, dus een halve tegelbreedte. Dat van de tweede tegel van boven ligt precies op een kwart van de breedte. De derde tegel mag slechts een zesde uitsteken. De vierde een achtste enzovoort. Om 1 tegel overhang te bewerkstelligen heb je een toren van 5 tegels nodig (overhang 1,14 tegel). Voor 2 tegels overhang een toren van 32 tegels, voor 3 tegels 227, enzovoort. Een oneindig hoge toren hangt oneindig ver over.
Geraadpleegde expert: dr. Rinke Wijngaarden, natuurkundige aan de Vrije Universiteit Amsterdam.

18) Waarom zie je in het centrum van je gezichtsveld minder sterren?

B, de rand van je netvlies is lichtgevoeliger dan het centrum. Je ziet minder sterren in het midden van je gezichtsveld omdat je oog daar veel kegeltjes en weinig staafjes heeft. Voor het zien via de kegeltjes heb je veel licht nodig omdat ze een hoge resolutie hebben en slechts een deel van het licht gebruiken. Je kunt hiermee veel details zien en kleur, maar alleen als er veel licht is. Bij weinig licht val je terug op de staafjes. Ze hebben minder licht nodig omdat ze al het beschikbare licht gebruiken en het licht over een groter gebied verzamelen. Aangezien er niet zoveel staafjes in het midden van je oog zitten (daar zitten immers de kegeltjes) zie je meer sterren aan de buitenkant, omdat daar meer staafjes zitten. Overdag is het centrum van je gezichtsveld superieur, nachts echter niet.
Geraadpleegde expert: prof. dr. Casper Erkelens, hoogleraar fysica van de mens, Universiteit Utrecht.

19) Wat gebeurt er als je over een zwembad maïzena rent?

A, je bereikt de overkant zonder weg te zakken. Door de regelmatige vorm van de korrels en door het gladde korreloppervlak vormen maïzenakorrels spontaan een dichtgepakte stapeling. In met water verzadigde maïzena liggen de korrels zeer dicht tegen elkaar en is de ruimte tussen de korrels gevuld met water. Om de pap te laten stromen, moet eerst meer ruimte tussen de korrels gemaakt worden. Die ruimte moet opgevuld worden met water. Dit kost tijd. Daarom gedraagt het materiaal zich stevig zolang de poriën niet opgevuld zijn. Als je over de maïzenapap loopt, zal die in eerste instantie bij elke stap je gewicht dragen. Je moet wel snel lopen, anders zak je er alsnog in.
Geraadpleegde experts: Han de Visser en dr. ir. Henderikus Allersma, onderzoekers Civiele Techniek en Geowetenschappen aan de Technische Universiteit Delft.

20) Als je denkt, wat wordt dan warmer of kouder?

C, je neus wordt kouder. Recent onderzoek van TNO heeft aangetoond dat er een verband is tussen mentale inspanning en de temperatuur van de neus. Die neemt af als mensen zich mentaal inspannen en neemt weer toe als ze in rust zijn. De afkoeling is groter naarmate de taak moeilijker is. We kunnen dat meten met een infraroodcamera. Vermoedelijk spelen bij het afkoelen van de neus twee mechanismen e en rol. De neus wordt minder doorbloed. En je gaat meer ademhalen waardoor er meer lucht langs je neus stroomt.
Geraadpleegde expert: Hans Veltman, TNO Defensie en Veiligheid.

quote:

Op woensdag 28 december 2005 20:31 schreef thabit het volgende:
Die vraag met die eenden geloof ik nog steeds niet. Ik liep vanmiddag langs een eendenvijver en daar waren de hoeken toch echt niet hetzelfde.

quote:

Op woensdag 28 december 2005 21:56 schreef bramiozo2002 het volgende:
Ja het ging om de boeggolf maar dan klopt het nog niet helemaal omdat de boeggolfhoek bij lage dieptes zeer zeker afhankelijk is van de snelheid (een eenvoudig lineair verband). Laagstaand water met gelijke diepte kan gebruikt worden om supersone lucht na te bootsen, daarbij is de golfhoek (de machkegel maw) dus direct afhankelijk van de snelheid.
Ze noemden een "diepe sloot" maar er zal altijd een geringe snelheidsafhankelijkheid zijn. Het hangt er ook vanaf of het water planeert (het voorwerp beweegt dan sneller dan de golfsnelheid), de lengte zal geen invloed hebben op de boeggolven.

quote:

Dat van die magnetron had toch te maken met de kristalstructuur van vast water ?

quote:

Op woensdag 28 december 2005 22:40 schreef Doderok het volgende:

[..]

En hele kleine eendjes? Speelt de oppervlaktespanning (capillaire golven) dan geen rol?
[..]

Ik vond vooral dat hun uitleg niet duidelijk maakte wat het verschil is tussen ijs opwarmen in een magnetron of op een hete kookplaat. Als je tegen iemand die geen kennis van fysica heeft zegt dat temperatuur een maat is voor de trilling van deeltjes, en je zegt dat in ijs de deeltjes vastzitten in een kristalrooster zodat ze niet tot trilling gebracht kunnen worden, dan zou die persoon besluiten dat ijs niet opgewarmd kan worden...

_{hopelijk komt nu niemand op het idee om een uiteenzetting te geven over vrijheidsgraden, Einstein-Bose en de wetten van de thermodynamica}