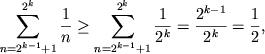Wetenschapsquiz

quote:

Op dinsdag 13 december 2005 12:16 schreef Quarks het volgende:

[..]

Deze reeks is dus niet eindig.
Dat wil zeggen, het verschil tussen 1000 en 1001 tegels maakt natuurlijk erg weinig uit voor de overhang van de bovenste tegel, maar toch blijft met de hoogte de maximale overhang toenemen.

Maar het feit dat met de hoogte de maximale overhang blijft toenemen impliceert natuurlijk niet dat de reeks niet eindig is

quote:

Op dinsdag 13 december 2005 12:16 schreef Quarks het volgende:

[..]

Dat dacht ik ook ja:

Harmonische reeks: 1 + 1/2 + 1/3 + 1/4 + 1/5 .... 1/n
Een harmonisch getal Hn is deze reeks tot stap n herhaald.
Dus harmonisch getal 5 = 1 + 1/2 + 1/3 + 1/4 + 1/5.

De maximale overhang voor een stapel van n tegels blijkt te zijn:
Hn / 2.

Voor 5 tegels is de maximale overhang 1,142
Voor 30 tegels is dat 1.997
Voor 100 tegels is dat 2.59
Voor 1000 tegels 3,74.

Deze reeks is dus niet eindig.
Dat wil zeggen, het verschil tussen 1000 en 1001 tegels maakt natuurlijk erg weinig uit voor de overhang van de bovenste tegel, maar toch blijft met de hoogte de maximale overhang toenemen.

Had ik nou niet iets gezegd over onzinnige bijdragen? Dit is echt pijnlijk om te lezen voor iedereen met een béétje wiskundig besef.

quote:

Op dinsdag 13 december 2005 12:20 schreef thabit het volgende:

[..]

Deze manier van redeneren is natuurlijk onjuist. Er zijn zat reeksen die het beschreven eindige gedrag hebben voor de waarden 5, 30, 100 en 1000 en toch niet divergeren.

Je hebt gelijk, in het uitleggen ben ik zelf niet zo goed.
Maar iedereen is het er nu wel over eens dat het antwoord oneindig moet zijn.

quote:

Op dinsdag 13 december 2005 12:23 schreef Koekepan het volgende:

[..]

Had ik nou niet iets gezegd over onzinnige bijdragen? Dit is echt pijnlijk om te lezen voor iedereen met een béétje wiskundig besef.

Mensen, mensen... vertel me liever hoe het met de eenden zit
En als je N(x) wil, dan heb je volgens mij de inverse van de digamma functie nodig...

quote:

Op dinsdag 13 december 2005 12:32 schreef Doderok het volgende:

[..]

Mensen, mensen... vertel me liever hoe het met de eenden zit

Volgens mij staat dat hier al ergens. .

offtopic..

Doderok Quarks

gave icoontjes

[ Bericht 6% gewijzigd door BdR op 13-12-2005 17:17:27 ]

Iedereen zegt 10->B (de trampoline, springveren moet je in je rugzak stoppen).

Wat echter als de trampoline superstrak gespannen is (zodat hij zo goed als niet veert)? Dan ben je toch echt beter af met verende schoenen.

10->B en 10->C is dus in ieder geval een fout antwoord bij een superstrakke trampoline.

Bij een meer verende trampoline ligt het misschien anders maar waar ligt dan het kantelpunt?

De vraag doet verder geen enkele uitspraak over de veerkracht van de trampoline of de schoenen dus blijft alleen antwoord A over.

[ Bericht 0% gewijzigd door yoppybt op 16-12-2005 14:08:51 ]

quote:

Op vrijdag 16 december 2005 13:54 schreef yoppybt het volgende:
Iedereen zegt 10->B (de trampoline, springveren moet je in je rugzak stoppen).

Wat echter als de trampoline superstrak gespannen is (zodat hij zo goed als niet veert)? Dan ben je toch echt beter af met verende schoenen.

10->B en 10->C is dus in ieder geval een fout antwoord bij een superstrakke trampoline.

Bij een meer verende trampoline ligt het misschien anders maar waar ligt dan het kantelpunt?

De vraag doet verder geen enkele uitspraak over de veerkracht van de trampoline of de schoenen dus blijft alleen antwoord A over.

Nee hoor. In het ideale geval is er geen energieverlies en bereikt hij sowieso terug zijn oorspronkelijke hoogte. Het gaat om "hij zet zich zo hard mogelijk af". Hoe stijver de ondergrond (trampoline + bladveren), hoe meer effect dit afzetten zal hebben. Zonder bladveren dus.

Ik heb het niet over het ideale geval (perfecte vering van de trampoline) maar over het andere uiterste: geen vering van de trampoline.
Stel dat hij zonder trampoline springt, gewoon op de grond. Dan bieden de veren onder de schoenen zeker wel een voordeel. Een strak gespannen trampoline gedraagt zich als de grond. Een normaal gespannen trampoline veert mee.
Hoe strak moet volgens jou de trampoline gespannen zijn opdat de veren onder de schoenen geen voordeel opleveren?

quote:

Op dinsdag 20 december 2005 18:09 schreef yoppybt het volgende:
Ik heb het niet over het ideale geval (perfecte vering van de trampoline) maar over het andere uiterste: geen vering van de trampoline.
Stel dat hij zonder trampoline springt, gewoon op de grond. Dan bieden de veren onder de schoenen zeker wel een voordeel. Een strak gespannen trampoline gedraagt zich als de grond. Een normaal gespannen trampoline veert mee.
Hoe strak moet volgens jou de trampoline gespannen zijn opdat de veren onder de schoenen geen voordeel opleveren?

Dat lijkt me een ingewikkelde berekening. Hoe strakker de trampoline, hoe meer energie verloren gaat doordat jou lichaam ipv de trampoline vervormt. Daar tegenover staat dat je harder kan afstoten. Waar het optimum ligt?

Maar de hele bedoeling van zowel een trampoline als springveren is zo hoog mogelijk te kunnen springen, dan is het logisch dat je van een 'goede' trampoline uitgaat en niet van één met de karakteristieken van een betonnen vloer.
Ik moet wel toegeven dat situatie complexer is dan ik eerst dacht. Toch ga ik voor antwoord B, vooral omdat er van een afstand van slechts één meter gesprongen wordt. Vanop zo'n hoogte zal je de maximale vervorming van een (doorsnee) trampoline nog niet bereiken. Daarom zal de extra vervorming die de springveren leveren nadelig werken bij het afzetten. Maar als je een maximale hoogte wil bereiken door herhaald op en neer te gaan, dan zouden de trekveren wel helpen...

_{NB: iets helemaal anders: omdat ik de oorspr. posts niet meer kan editeren: waar ik bij de eendjes over de hoogte vd golven sprak moet het natuurlijk lengte zijn}

[ Bericht 1% gewijzigd door Doderok op 21-12-2005 17:33:18 ]

In het discussieforum van de NWQ kwam ik het volgende tegen bij de vraag over de wijnvlek:



Heb het geprint en de twee vakjes uitgeknipt. Ze zijn precies even donker.
Verder heb ik ook wel wat wijnvlekken op onze mexicaans eiken salontafel, als ik die daaruit zou kunnen knippen, weet ik vrijwel zeker dat de vlek overal even donker is.

(Ja, ik weet dat ik niet meer in kan zenden, maar vind het alsnog leuk om de antwoorden te zoeken voor zaterdag.)

quote:

Op woensdag 21 december 2005 00:03 schreef Gia het volgende:
In het discussieforum van de NWQ kwam ik het volgende tegen bij de vraag over de wijnvlek:

[afbeelding]

Heb het geprint en de twee vakjes uitgeknipt. Ze zijn precies even donker.
Verder heb ik ook wel wat wijnvlekken op onze mexicaans eiken salontafel, als ik die daaruit zou kunnen knippen, weet ik vrijwel zeker dat de vlek overal even donker is.

(Ja, ik weet dat ik niet meer in kan zenden, maar vind het alsnog leuk om de antwoorden te zoeken voor zaterdag.)

Net op tijd (min of meer) aan dit topic gedacht toen ik enkele wijnvlekken wou wegvegen:

Rechts een vlek, links een gefotoshopt vlak van egale kleur.
Op het hout is plastic aangebracht, mogelijk dat daardoor enkel een rand overbleef.
In ieder geval is duidelijk dat men bij een egaal gekleurde vlek de randen niet automatisch als donkerder ziet. (de wereld zou er raar uitzien)

quote:

Op woensdag 21 december 2005 01:42 schreef Doderok het volgende:

[..]

Net op tijd (min of meer) aan dit topic gedacht toen ik enkele wijnvlekken wou wegvegen:
[afbeelding]
Rechts een vlek, links een gefotoshopt vlak van egale kleur.
Op het hout is plastic aangebracht, mogelijk dat daardoor enkel een rand overbleef.
In ieder geval is duidelijk dat men bij een egaal gekleurde vlek de randen niet automatisch als donkerder ziet. (de wereld zou er raar uitzien)

Ik zie bij dat egaal gekleurde vlak wel een donkerdere rand.

Maar goed. Zaterdag weten we het.

Vind het sowieso elk jaar een vermakelijk programma.

Televisie aan, het is zo ver!

22.15 nederland 3.

voor mijn gevoel zaten er toch aan de hand van de antwoorden flink wat haken en ogen aan de vragen in de wetenschapsquiz, ff kort behandeld:

vraag 5. onjuist en is ook geschrapt

vraag 6. Kun je een geslaagde foto maken van een fata morgana?

Ik vind dit persoonlijk een foute vraagstelling.. Het gaat hierbij puur om je persoonlijk vertaling van de woorden 'fata morgana' De van Dale zegt hierover het volgende: 1. meervoudige luchtspiegeling, bla bla.. dat kennen we idd van hitte dat je die breking ziet en hier is een foto van te maken MAAR van dale 2. luchtkasteel, illusie, utopie, visioen... Het 2e woord zegt het al! iets wat er niet is kan je niet fotograferen!

Vraag 16: Als een fotograaf zijn camera 45 graden scheef houdt, vinden we alles op de foto hinderlijk scheef staan. Maar als je je hoofd scheef houdt, heb je daar geen last van. Hoe komt dat?

Weet niet wat ik van de vraag moet denken, betekent het ' daar' het ' hinderlijk scheef staan op de foto' of betekende het 'het hinderlijk scheef staan' Het antwoord was geloof ik C, en als verklaring werd het corrigeren van de hersenen door een nek beweging, zijn gaan dus voor 'hinderlijk scheef staan'. A is dus ook interpreteerbaar als het corrigeren van je hersenen voor de foto, omdat je wil dat de huzien rechtstaan ed.. maar dit is dus slechts weer een taal-kundigvraagstuk...

Vraag 19: Een zwembad gevuld met maïzena wordt gemengd met water totdat een dikke pap ontstaat. Wat gebeurt er als je over het mengsel naar de overkant probeert te rennen?

compleet belachelijke vraag mijns inziens! wat is een 'dikke pap'? het ligt er bij deze vraag puur aan hoeveel maizena je erin gooit! hoe meer erin hoe beter je er over kan lopen uiteraard

correct me if i'm wrong natuurlijk!

Ik vond het maar een matige aflevering dit jaar. Ik had het idee dat de vragen iets makkelijker waren dan anders. Daarnaast was de show zeer matig van opzet. Totaal geen diepgang, een zogenaamd lab dat niks toevoegd en er een beetje tussengeplakt is. Ik verlang terug naar Wim T. Schippers!!

Ik wil Ernie terug

Ja, ze zijn een beetje zoekende sinds Wim weg is. Maar ik vind de show niet per se minder goed. De vragen wel, ja, maar dat komt ook wel doordat ik nou alles wel een keer voorbij heb zien komen.

ik vind de show juist wel prima zo! de principes worden goed uitgelegd, maar ook lekker simpel zodat iedereen het begrijpt. Je hebt geen krijsend koor er door hene die elke 10 sec iets van zich wil laten horen, geen a-relaxete assistente...met Sophie mogen we toch in onze handjes wrijven...een beteje halve proefjes om het aan te tonen en leuk te houden. en gene zeikende Schippres met z'n a-relaxte stem.. de show was prima.... alleen de vragen sja....

Mmmh, ik vond het niveau belachelijk laag. In plaats van dat ze even een duidleijk, maar wel correcte uitleg gaven, kwam er een soort brugklasuitlegje waar je nog niks mee kon. Bij die toren van stenen bijvoorbeeld. Die is simpel uit leggen door te zeggen dat de formule van die toren (1/2n) divergeert. Dan ben je dus gelijk klaar...

Maja ik zal wel weer te kritisch zijn...