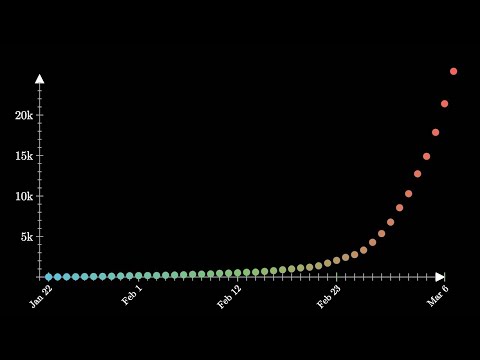
Wiskundige kijk op de verspreiding van een virus.
Het getal in de derde kolom moet dan nog flink naar beneden:
| 1 2 3 4 5 6 7 8 9 10 11 | 27-feb 1 28-feb 2 2,00 29-feb 6 3,00 1-mrt 11 1,83 2-mrt 18 1,64 3-mrt 23 1,28 4-mrt 38 1,65 5-mrt 82 2,16 6-mrt 128 1,56 7-mrt 188 1,47 8-mrt 265 1,41 |
Komen we voorlopig niet achter omdat veel milde besmettingen niet geregistreerd worden.
Dit klopt niet, je moet de delta’s op elkaar delenquote:Op zondag 8 maart 2020 20:42 schreef vosss het volgende:
We zitten dus nog niet op het inflection point.
Het getal in de derde kolom moet dan nog flink naar beneden:
[ code verwijderd ]
Klopt mijn lijstje niet?quote:Op zondag 8 maart 2020 20:44 schreef Faraday01 het volgende:
[..]
Dit klopt niet, je moet de delta’s op elkaar delen
Is een lijstje wat ik vanochtend gemaakt heb toen ik net wakker was
dit is de verhouding van het totaal aantal besmettingen tussen vandaag en gisteren. Om de groeifactor grofweg te bepalen moet de toename van vandaag gedeeld worden door de toename van gisteren. De trend tussen de dagen zegt dan iets over de versnelling of vertraging van de groei van het aantal gevallen.quote:
[..]
Klopt mijn lijstje niet?
Is een lijstje wat ik vanochtend gemaakt heb toen ik net wakker was
| 1 2 3 4 5 6 7 8 9 10 | 28-feb 2 1 1,00 29-feb 6 4 4,00 1-mrt 11 5 1,25 2-mrt 18 7 1,40 3-mrt 23 5 0,71 4-mrt 38 15 3,00 5-mrt 82 44 2,93 6-mrt 128 46 1,05 7-mrt 188 60 1,30 8-mrt 265 77 1,28 |
In elk geval zitten we nog steeds ver van de "1" af.
waar zitten we volgende maand?quote:
Er is veel te weinig data voor een betrouwbare vergelijkingquote:
De vraag is in hoeverre deze cijfers een goed beeld geven van de werkelijkheid. Als er straks genoeg besmettingen zijn is het niet meer bij te houden qua tests en dan kloppen je cijfers niet echt meer vrees ik.
Daarom, hooguit handig om een goed idee te vormen, maar betrouwbaar gaat het niet zijn, omdat de getallen alleen maar afhangen van het aantal gedane testen.quote:
[..]
Er is veel te weinig data voor een betrouwbare vergelijking
Ik denk dat dat zeer afhankelijk gaat zijn van hoe Nederland, en alle andere landen om ons heen, hier op gaan reageren.quote:
maar als t zo snel verspreid zoals t nu doet.quote:
[..]
Ik denk dat dat zeer afhankelijk gaat zijn van hoe Nederland, en alle andere landen om ons heen, hier op gaan reageren.
)quote:Op zondag 8 maart 2020 20:33 schreef Arcee het volgende:
Wiskundige kijk op de verspreiding van een virus.
quote:
quote:
Kijken we even mee, wiskundegeniën!?quote:
[..]
Er is geen exponentiële groei gaande tot nu toe.
Is het in NL exponentieel dan?quote:
[..]
Kijken we even mee, wiskundegeniën!?
[..]
[..]
[..]
Ja. Hoe kom je anders van 1 naar 100!??quote:
ja vorige week was er bijna niemand hier met corona, nu ineens een paar 100. volgende week duizenden?quote:
Het zal je de komende weken duidelijk worden dat die vergelijking geheel mank gaat EU ≠ China.quote:
Ik denk dat we Italië met Wuhan moeten vergelijken en de rest van Europa zijn de omliggende Chinese provincieen.
Dat verwacht ik ook.quote:
[..]
Het zal je de komende weken duidelijk worden dat die vergelijking geheel mank gaat EU ≠ China.
China nam vanaf dat moment namelijk wél stevige maatregelen.
Dit.quote:
In de Filipijnen is de gezondheidszorg erg belabberd en men heeft vaak gewoon geen geld om naar de dokter te gaan.
Onder normale omstandigheden staan er vaak enorm lange wachtrijen voor de ziekenhuizen; de middenklasse met gewone kwaaltjes. Met een beetje pech sta je er de hele dag en kom je gewoon niet aan de beurt (tenzij je vooraf een afspraak maakt, wat bijna niemand doet.)
Vandaag is het aantal corona-gevallen spontaan verdubbeld van 10 naar 20; de rijke upper class die naar Zuid-Korea enzo gaat en ziek thuis komt en besluit om naar een privékliniek te gaan voor een test.
De armere mensen zal het allemaal niet boeien, ook al zouden ze een ziekenhuisbezoek kunnen betalen. Tuberculose tiert er welig omdat men elkaar blijft infecteren door 1 glas met elkaar te delen met drinksessies en men hoest gewoon rond zich heen zonder zich om anderen te bekommeren. Algemene hygiëne is in bepaalde delen van het land ook ver te zoeken.
Daarbij heb je dat veel mensen bijna alleen witte rijst eten met een klein beetje vis er bij en soms wat fruit. Groenten eten ze er een stuk minder, dus de weerstand is bij veel mensen ook niet zo super.
Die 20 bekende gevallen is dan ook een lachertje, het werkelijke aantal zal er een veelvoud van zijn.
Het is zeker niet lineair iig.quote:
Verre van...quote:
[..]
Het is zeker niet lineair iig.
En hoe noemen we groei als die niet meer lineair is!? Juist! Exponentieel.
Serieuze vraag: zie jij een toename in de aantallen nieuwe besmettingen in NL? Of blijft dat getal min of meer constant?quote:
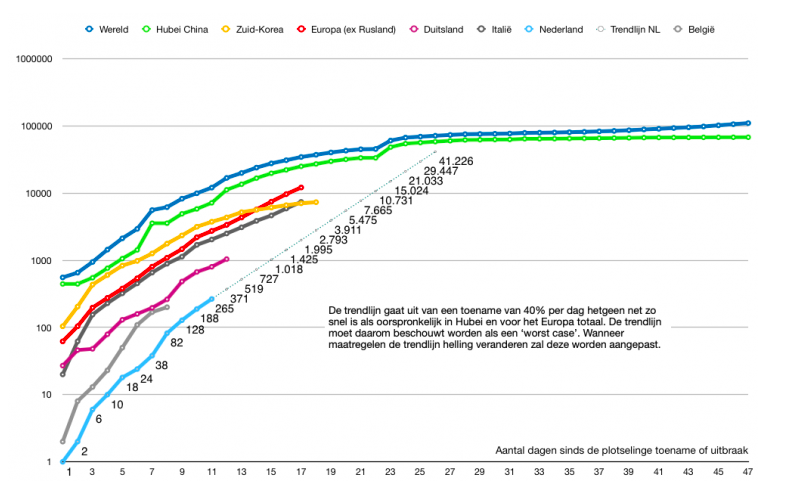
@_I plaatste deze in het centrale topic, maar daar gaat het zo hard dat het voor mijn gevoel verzande..
Wat ik me afvroeg.. Je ziet in de 1e week echt exponentiele groei.. Maar het vlakt al aardig af (logaritmisch) na een week en na twee weken helemaal geen groei meer.
Voorbeelden: China, Zuid Korea
Zou het dan toch zo zijn dat het snel en heftig komt, maar ook vrij snel weer uitraast??
Daarom vind ik die voorspelling voor NL te pessimistisch
Hoop op jouw antwoord, maar het zou ook kunnen dat je maar 1000 testen per dag kan doen, dan wordt de lijn vanzelf een kromme.quote:
[ afbeelding ]
@:_I plaatste deze in het centrale topic, maar daar gaat het zo hard dat het voor mijn gevoel verzande..
Wat ik me afvroeg.. Je ziet in de 1e week echt exponentiele groei.. Maar het vlakt al aardig af (logaritmisch) na een week en na twee weken helemaal geen groei meer.
Voorbeelden: China, Zuid Korea
Zou het dan toch zo zijn dat het snel en heftig komt, maar ook vrij snel weer uitraast??
Daarom vind ik die voorspelling voor NL te pessimistisch
Ja, ik heb ook heel veel dubieuze glaasjes gedeeld in de Filipijnen jaquote:Op maandag 9 maart 2020 10:13 schreef ToT het volgende:
In sommige landen kan het echt exploderen.
In de Filipijnen is de gezondheidszorg erg belabberd en men heeft vaak gewoon geen geld om naar de dokter te gaan.
Onder normale omstandigheden staan er vaak enorm lange wachtrijen voor de ziekenhuizen; de middenklasse met gewone kwaaltjes. Met een beetje pech sta je er de hele dag en kom je gewoon niet aan de beurt (tenzij je vooraf een afspraak maakt, wat bijna niemand doet.)
Vandaag is het aantal corona-gevallen spontaan verdubbeld van 10 naar 20; de rijke upper class die naar Zuid-Korea enzo gaat en ziek thuis komt en besluit om naar een privékliniek te gaan voor een test.
De armere mensen zal het allemaal niet boeien, ook al zouden ze een ziekenhuisbezoek kunnen betalen. Tuberculose tiert er welig omdat men elkaar blijft infecteren door 1 glas met elkaar te delen met drinksessies en men hoest gewoon rond zich heen zonder zich om anderen te bekommeren. Algemene hygiëne is in bepaalde delen van het land ook ver te zoeken.
Daarbij heb je dat veel mensen bijna alleen witte rijst eten met een klein beetje vis er bij en soms wat fruit. Groenten eten ze er een stuk minder, dus de weerstand is bij veel mensen ook niet zo super.
Die 20 bekende gevallen is dan ook een lachertje, het werkelijke aantal zal er een veelvoud van zijn.
Tagay
Haha, proost!quote:
[..]
Ja, ik heb ook heel veel dubieuze glaasjes gedeeld in de Filipijnen ja
Tagay
Ja ik ook hoor, met een bokkenfuif, en een keer ergens op een strand.
Ik kende er niemand van, maar ze waren heel enthousiast dat een "Americano" zo goed kon zuipen!
Van 1 ranzige alcoholist was ik ff minder blij dat die uit het zelfde glas dronk.
Dat komt denk ik ook voor een groot deel door de quarantainemaatregelen in beide landen. Bijna iedereen zit thuis, dus mensen kunnen in principe alleen andere gezinsleden besmetten. Ik ben benieuwd wat er gaat gebeuren zodra iedereen in China weer aan het werk gaat..quote:
Wat ik me afvroeg.. Je ziet in de 1e week echt exponentiele groei.. Maar het vlakt al aardig af (logaritmisch) na een week en na twee weken helemaal geen groei meer.
Voorbeelden: China, Zuid Korea
Zou het dan toch zo zijn dat het snel en heftig komt, maar ook vrij snel weer uitraast??
Daarom vind ik die voorspelling voor NL te pessimistisch
Volgens mij, en ik laat mij graag verbeteren, komt dat door de Y-as. Dat geeft een vertekend beeldquote:
[ afbeelding ]
@:_I plaatste deze in het centrale topic, maar daar gaat het zo hard dat het voor mijn gevoel verzande..
Wat ik me afvroeg.. Je ziet in de 1e week echt exponentiele groei.. Maar het vlakt al aardig af (logaritmisch) na een week en na twee weken helemaal geen groei meer.
Voorbeelden: China, Zuid Korea
Zou het dan toch zo zijn dat het snel en heftig komt, maar ook vrij snel weer uitraast??
Daarom vind ik die voorspelling voor NL te pessimistisch
En wat niet meegenomen wordt, is het aantal mensen dat getest wordt. Stel een land test niemand, dan zij er dus ook geen besmettingen
Zo kan ik mij niet voorstellen dat het probleem in China nagenoeg opgelost is. Natuurlijk ben ik geen viruloog, maar er worden daar ineens geweldige resultaten geboekt.
De Y-as geeft helemaal geen vertekend beeld. Een logaritmische as is juist veel duidelijker wanneer het gaat om zich exponentieel ontwikkelende processen. Ik kan mij juist goed voorstellen dat de groei in China inmiddels grotendeels voorbij is gezien de grote bestrijdingsinzet. Die trens zie je daar immers al zeker 2 weken en eigenlijk al langer.quote:Op maandag 9 maart 2020 15:25 schreef opgebaarde het volgende:
[..]
Volgens mij, en ik laat mij graag verbeteren, komt dat door de Y-as. Dat geeft een vertekend beeld
En wat niet meegenomen wordt, is het aantal mensen dat getest wordt. Stel een land test niemand, dan zij er dus ook geen besmettingen
Zo kan ik mij niet voorstellen dat het probleem in China nagenoeg opgelost is. Natuurlijk ben ik geen viruloog, maar er worden daar ineens geweldige resultaten geboekt.
Welnee, Duterte geeft gewoon zijn doodsekaders een nieuwe taak: ipv elke drugsdealer die ze zien, moeten ze vanaf nu iedereen die hoest volpompen met lood.quote:
In sommige landen kan het echt exploderen.
In de Filipijnen is de gezondheidszorg erg belabberd en men heeft vaak gewoon geen geld om naar de dokter te gaan.
Onder normale omstandigheden staan er vaak enorm lange wachtrijen voor de ziekenhuizen; de middenklasse met gewone kwaaltjes. Met een beetje pech sta je er de hele dag en kom je gewoon niet aan de beurt (tenzij je vooraf een afspraak maakt, wat bijna niemand doet.)
Vandaag is het aantal corona-gevallen spontaan verdubbeld van 10 naar 20; de rijke upper class die naar Zuid-Korea enzo gaat en ziek thuis komt en besluit om naar een privékliniek te gaan voor een test.
De armere mensen zal het allemaal niet boeien, ook al zouden ze een ziekenhuisbezoek kunnen betalen. Tuberculose tiert er welig omdat men elkaar blijft infecteren door 1 glas met elkaar te delen met drinksessies en men hoest gewoon rond zich heen zonder zich om anderen te bekommeren. Algemene hygiëne is in bepaalde delen van het land ook ver te zoeken.
Daarbij heb je dat veel mensen bijna alleen witte rijst eten met een klein beetje vis er bij en soms wat fruit. Groenten eten ze er een stuk minder, dus de weerstand is bij veel mensen ook niet zo super.
Die 20 bekende gevallen is dan ook een lachertje, het werkelijke aantal zal er een veelvoud van zijn.
Die vrolijke snuiters op crossmotoren hebben de afgelopen paar jaar 30.000 vermeende drugdealers omgelegd, dus een paar hoesters krijgen ze ook wel te pakken
Hehehe dan blaffen ze ook ladingen mensen met TBC overhoop.quote:
[..]
Welnee, Duterte geeft gewoon zijn doodsekaders een nieuwe taak: ipv elke drugsdealer die ze zien, moeten ze vanaf nu iedereen die hoest volpompen met lood.
Die vrolijke snuiters op crossmotoren hebben de afgelopen paar jaar 30.000 vermeende drugdealers omgelegd, dus een paar hoesters krijgen ze ook wel te pakken
Dat is toch geen probleem!? Die 30.000 zogenaamde drugdealers waren ook lang niet allemaal daadwerkelijk drugsdealer.quote:
[..]
Hehehe dan blaffen ze ook ladingen mensen met TBC overhoop.
Het land heeft deze oplossing gewoon nodig, heb ik gelezen op de Frontpage hier. Ik als naïeve westerling begrijp dat niet.
SPOILERDat ik dat niet zou begrijpen omdat het ik uit het westen kom, is een beetje kortzichtig. Een tijdje terug begrepen sommige mensen hier in Europa wel degelijk wat de oplossing was. Noemden ze de 'Endlösung'. Hebben ze ook in de praktijk gebracht. Met nog meer succes dan oom Duterte
SPOILERWel grappig dat de ultrarechtse schreeuwertjes dus net zo veel last hebben van cultuurrelativisme als de mensen ter linkerzijde.
[ Bericht 9% gewijzigd door Puntenjager op 09-03-2020 17:28:53 ]
| 1 2 3 4 5 6 7 8 9 10 11 | 28-feb 2 1 1,00 29-feb 6 4 4,00 1-mrt 11 5 1,25 2-mrt 18 7 1,40 3-mrt 23 5 0,71 4-mrt 38 15 3,00 5-mrt 82 44 2,93 6-mrt 128 46 1,05 7-mrt 188 60 1,30 8-mrt 265 77 1,28 9-mrt 321 56 0,73 |
Jaaah, nagenoeg perfect 1 die laatste kolom. Niks exponentieels aan.quote:
Ik denk dat je kwadratisch en exponentieel door elkaar haalt. Alles behalve x1 (en x0) is exponentieel.quote:
[..]
Jaaah, nagenoeg perfect 1 die laatste kolom. Niks exponentieels aan.
Een vermenigvuldigingsfactor (tussen opeenvolgende generaties) groter dan 1 noemen we toch exponentieel!?quote:
[..]
Ik denk dat je kwadratisch en exponentieel door elkaar haalt. Alles behalve x1 (en x0) is exponentieel.
Nou, ik zie in die laatste kolom een vermenigvuldigingsfactor die weliswaar niet constant is, maar die het grootste deel van de tijd flink boven de 1 ligt.
quote:
Wiskundige kijk op de verspreiding van een virus.
Topic kan dichtquote:
[..]
Exponentieel is een wiskundige term. Die is hier niet van toepassing.
SPOILER
Het getal blijft niet constant.quote:
[..]
Serieuze vraag: zie jij een toename in de aantallen nieuwe besmettingen in NL? Of blijft dat getal min of meer constant?
Bij exponentiële groei wordt een hoeveelheid telkens met hetzelfde getal g, de groeifactor, vermenigvuldigd.
Klopt, maar het aantal nieuwe gevallen blijkt elke dag te groeien. Om precies te zijn met een vermeningvuldigingsfactor ruim groter dan 1 tov de situatie een dag ervoor.quote:Op maandag 9 maart 2020 22:19 schreef Mickytjuh het volgende:
[..]
Het getal blijft niet constant.
Bij exponentiële groei wordt een hoeveelheid telkens met hetzelfde getal g, de groeifactor, vermenigvuldigd.
Alleen die factor g is inderdaad niet perfect constant. Echter is dat nodig!?? Zo ja, dan bestaat exponentiële groei alleen in wiskundeboeken, want in de realiteit zal die factor g altijd wel een beetje zwabberen. In het onderhavige coronageval niet in de laatste plaats door grote meetfouten en onregelmatige rapportagemomenten.
• Dus aan jou de vraag hoe constant die factor g moet zijn voordat jij een groei exponentieel noemt.
• En ben je het met me eens dat nieuwe besmettingen voortkomen uit de besmette gevallen die er op dat moment al zijn!?
Dit is zo ongeveer de definitie van exponentiële groei. Zie ook dat filmpje in de OP.
• In dat filmpje hierboven komt een correlatiecoëfficient R naar voren van 0,95. Statistici beschouwen dat als een zeer grote mate van correlatie. Ben jij het daarmee eens of vind jij 0,95 niet genoeg!?
[ Bericht 0% gewijzigd door Puntenjager op 09-03-2020 22:56:44 ]
| 1 2 3 4 5 6 7 8 9 10 11 12 | 28-feb 2 1 1,00 29-feb 6 4 4,00 1-mrt 11 5 1,25 2-mrt 18 7 1,40 3-mrt 23 5 0,71 4-mrt 38 15 3,00 5-mrt 82 44 2,93 6-mrt 128 46 1,05 7-mrt 188 60 1,30 8-mrt 265 77 1,28 9-mrt 321 56 0,73 10-mrt 382 61 1,09 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 | 28-feb 2 1 1,00 29-feb 6 4 4,00 1-mrt 11 5 1,25 2-mrt 18 7 1,40 3-mrt 23 5 0,71 4-mrt 38 15 3,00 5-mrt 82 44 2,93 6-mrt 128 46 1,05 7-mrt 188 60 1,30 8-mrt 265 77 1,28 9-mrt 321 56 0,73 10-mrt 382 61 1,09 11-mrt 503 121 1,98 |
Niks aan het handje, jongens. Geen correlatie tussen de momentane omvang van de besmette populatie en het aantal nieuwe besmettingen. Geen exponentiële groei dus.quote:
Weinig raars aan. Bier koop je meestal in een sixpack. Soms zelfs in een kratjequote:
Meh, de gezinsleden worden niet meer getest om tests te sparen. Het is nu zo, 1 corona?,dan heel het gezin in isolatie. Dus deze getallen zeggen nu niet zoveel meer.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 28-feb 2 1 1,00 29-feb 6 4 4,00 1-mrt 11 5 1,25 2-mrt 18 7 1,40 3-mrt 23 5 0,71 4-mrt 38 15 3,00 5-mrt 82 44 2,93 6-mrt 128 46 1,05 7-mrt 188 60 1,30 8-mrt 265 77 1,28 9-mrt 321 56 0,73 10-mrt 382 61 1,09 11-mrt 503 121 1,98 12-mrt 614 111 0,92 13-mrt 804 190 1,71 |
Ziet er nog niet bepaald bemoedigend uit die vierde kolom. Ik druk mij voorzichtig uit. RIP aan de nabestaandenquote:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | 28-feb 2 1 1,00 29-feb 6 4 4,00 1-mrt 11 5 1,25 2-mrt 18 7 1,40 3-mrt 23 5 0,71 4-mrt 38 15 3,00 5-mrt 82 44 2,93 6-mrt 128 46 1,05 7-mrt 188 60 1,30 8-mrt 265 77 1,28 9-mrt 321 56 0,73 10-mrt 382 61 1,09 11-mrt 503 121 1,98 12-mrt 614 111 0,92 13-mrt 804 190 1,71 14-mrt 959 155 0,82 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | 28-feb 2 1 1,00 29-feb 6 4 4,00 1-mrt 11 5 1,25 2-mrt 18 7 1,40 3-mrt 23 5 0,71 4-mrt 38 15 3,00 5-mrt 82 44 2,93 6-mrt 128 46 1,05 7-mrt 188 60 1,30 8-mrt 265 77 1,28 9-mrt 321 56 0,73 10-mrt 382 61 1,09 11-mrt 503 121 1,98 12-mrt 614 111 0,92 13-mrt 804 190 1,71 14-mrt 959 155 0,82 15-mrt 1135 176 1,14 |
quote:
Gele lijn is de groeifactor per dag. De rode lijn is de groeifactor gemiddeld over de laatste 2 dagen. De cijfers komen uit de post die quote.
Verkijk je niet op dat de grafiek mooi omlaag gaat. Een facor van slechts 1,15 betekent al een verdubbeling in 5 dagen!
Ben jij kleurenblind trouwens?quote:
[..]
[ afbeelding ]
Gele lijn is de groeifactor per dag. De rode lijn is de groeifactor gemiddeld over de laatste 2 dagen. De cijfers komen uit de post die quote.
Verkijk je niet op dat de grafiek mooi omlaag gaat. Een facor van slechts 1,15 betekent al een verdubbeling in 5 dagen!
Ja, lichtjes.quote:
Maar wat voor kleuren vind jij het het dan?
Groen en geel.quote:
[..]
Ja, lichtjes.
Maar wat voor kleuren vind jij het het dan?
Ik vind het prima.quote:
Vooral groentinten en bruintinten die richting rood gaan, kan ik niet goed onderscheiden. En 8 of 10% van de mannen met mij. Vrouwen zijn veel minder vaak kleurenblind.
Tussen grasgroen, felrood en poepbruin zie ik een groot verschil, maar niet als het tinten zijn die meer naar elkaar toe liggen. Zeker niet als het dunne lijntjes of kleine vlakjes zijn.
[ Bericht 0% gewijzigd door Puntenjager op 16-03-2020 09:38:12 ]
Als dat het enige is, dan valt daar wel mee te leven toch.quote:
[..]
Ik vind het prima.
Vooral groentinten en bruintinten die richting rood gaan, kan ik niet goed onderscheiden. En 8 of 10% van de mannen met mijn. Vrouwen zijn veel minder vaak kleuren.
Tussen grasgroen, felrood en poepbruin zie ik een groot verschil, maar niet als het tinten zijn die meer naar elkaar liggen. Zeker niet als het dunne lijntjes of kleine vlakjes zijn.
Het was gewoon een beetje grappig.
Ik zie jou iig als helderblauwquote:
[..]
Als dat het enige is, dan valt daar wel mee te leven toch.
Het was gewoon een beetje grappig.
Geel en groen.quote:
[..]
Ja, lichtjes.
Maar wat voor kleuren vind jij het het dan?
Maar maakt ook niet uit hoor. Het zijn ook verdomd dunne lijntjes.
quote:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | 28-feb 2 1 1,00 29-feb 6 4 4,00 1-mrt 11 5 1,25 2-mrt 18 7 1,40 3-mrt 23 5 0,71 4-mrt 38 15 3,00 5-mrt 82 44 2,93 6-mrt 128 46 1,05 7-mrt 188 60 1,30 8-mrt 265 77 1,28 9-mrt 321 56 0,73 10-mrt 382 61 1,09 11-mrt 503 121 1,98 12-mrt 614 111 0,92 13-mrt 804 190 1,71 14-mrt 959 155 0,82 15-mrt 1135 176 1,14 16-mrt 1413 278 1,58 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | 28-feb 2 1 1,00 29-feb 6 4 4,00 1-mrt 11 5 1,25 2-mrt 18 7 1,40 3-mrt 23 5 0,71 4-mrt 38 15 3,00 5-mrt 82 44 2,93 6-mrt 128 46 1,05 7-mrt 188 60 1,30 8-mrt 265 77 1,28 9-mrt 321 56 0,73 10-mrt 382 61 1,09 11-mrt 503 121 1,98 12-mrt 614 111 0,92 13-mrt 804 190 1,71 14-mrt 959 155 0,82 15-mrt 1135 176 1,14 16-mrt 1413 278 1,58 17-mrt 1705 292 1,05 18-mrt 2051 346 1,18 |
Hopelijk zien we met de genomen maatregelen dat de groeifactor onder de 1 gaat duiken de komende dagen / weken.quote:
[..]
[ afbeelding ]
Gele lijn is de groeifactor per dag. De rode lijn is de groeifactor gemiddeld over de laatste 2 dagen. De cijfers komen uit de post die quote.
Verkijk je niet op dat de grafiek mooi omlaag gaat. Een facor van slechts 1,15 betekent al een verdubbeling in 5 dagen!
Volgens mij klopt dit niet, bijvoorbeeld 0,82 op 14 maart? Dat zou toch een afname betekenen?quote:
Snap het nu, dat % is de verandering van de toename.
Het is misschien beter om naar het aantal sterfgevallen te kijken. Het gemeten aantal besmettingen is nogal afhankelijk van hoeveel er getest wordt.quote:
[..]
Hopelijk zien we met de genomen maatregelen dat de groeifactor onder de 1 gaat duiken de komende dagen / weken.
twitter:kortewijn twitterde op donderdag 19-03-2020 om 13:59:51@geertwilderspvv Beste mijnheer Wilders en mijnheer Baudet @geertwilderspvv @thierrybaudet en @NOS jammer genoeg is dat "normaal" voor het fenomeen exponentiële groei met een dagelijkse vermenigvuldiging met 1.2 tot 1.4 ik heb er een grafiek van gemaakt. https://t.co/MNYzAczrFF reageer retweet
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | 28-feb 2 1 1,00 29-feb 6 4 4,00 1-mrt 11 5 1,25 2-mrt 18 7 1,40 3-mrt 23 5 0,71 4-mrt 38 15 3,00 5-mrt 82 44 2,93 6-mrt 128 46 1,05 7-mrt 188 60 1,30 8-mrt 265 77 1,28 9-mrt 321 56 0,73 10-mrt 382 61 1,09 11-mrt 503 121 1,98 12-mrt 614 111 0,92 13-mrt 804 190 1,71 14-mrt 959 155 0,82 15-mrt 1135 176 1,14 16-mrt 1413 278 1,58 17-mrt 1705 292 1,05 18-mrt 2051 346 1,18 19-mrt 2460 409 1.18 20-mrt 2994 534 1.31 21-mrt 3631 637 1.19 22-mrt 4204 573 0.90 23-mrt 4749 545 0.95 24-mrt 5560 811 1.49 25-mrt 6412 852 1.05 26-mrt 7431 1019 1.20 27-mrt 8603 1127 1.11 28-mrt 9762 1159 1.03 |
Kan wel eens meevallen, weinig mensen met overgewicht daar. En ze hebben een goede afweer waarschijnlijk.quote:
Ik ben benieuwd hoe exponentieel COVID-19 zich in de slums van India gaat ontwikkelen. Dat gaat echt een humanitaire ramp worden.
Muah, overgewicht hebben is daar ook een soort statussymbool daar. Ik ken de situatie niet maar volgens mij is overgewicht ook daar gewoon een probleem.quote:
[..]
Kan wel eens meevallen, weinig mensen met overgewicht daar.
Het gebrek aan goede gezondheidszorg trouwens ook.
ten zij ze hele dikke bananen hebben heeft deze foto een verkeerde aspect ratio.quote:
[..]
Muah, overgewicht hebben is daar ook een soort statussymbool daar. Ik ken de situatie niet maar volgens mij is overgewicht ook daar gewoon een probleem.
Het gebrek aan goede gezondheidszorg trouwens ook.
[ afbeelding ]
Dit is een foto die ondersteunt dat obesitas een probleem is in India.quote:
[..]
ten zij ze hele dikke bananen hebben heeft deze foto een verkeerde aspect ratio.
Je bedoelt fotoshop?quote:
[..]
ten zij ze hele dikke bananen hebben heeft deze foto een verkeerde aspect ratio.
Enige jammere en gevaarlijke aan dit soort overzichten is, is dat dit alleen van de geteste mensen komt. Er is geen inzicht in mensen die wel corona hebben maar niet getest zijn.quote: