SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Kickje?
Ik zit al een poosje te peinzen over een probleem wat zich afspeelt binnen de complexe functietheorie maar eigenlijk gaat over evolutievergelijkingen.
Enfin, als volgt:
Zij X een Banach ruimte en A een lineaire, begrensde operator op X. Dan weten we dat:
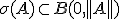
En voor alle s in de resolventen verzameling bestaat er een Laurent series ontwikkeling:
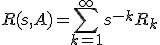
Waar Rk weer lineaire, begrensde operatoren op X zijn.
Schrijf nu sI-A = s(I-A/s) en pas een Neumann ontwikkeling toe:
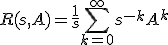
En het volgt al snel dat Rk = Ak-1
Dan volgt het echte vraagstuk:
Bereken:
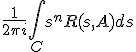voor n = 0,1,2.. waar C een contourintegraal is (tegen de klok in) die het spectrum van A omvat.
Nu weten we dat de resolvent geen analytische voortzetting bevat in het spectrum van A, maar complexe functietheorie vertelt ons dat we integraal kunnen evalueren door naar het residu te kijken. Nu weten we niet of het spectrum überhaupt aftelbaar is, dus nu mijn vraag, hoe gebruiken we complexe functietheorie om deze integraal te evalueren?
Merk tevens op dat de resolvent een operator is, en we dus integreren over lineaire operators op X.
Ik zit al een poosje te peinzen over een probleem wat zich afspeelt binnen de complexe functietheorie maar eigenlijk gaat over evolutievergelijkingen.
Enfin, als volgt:
Zij X een Banach ruimte en A een lineaire, begrensde operator op X. Dan weten we dat:
En voor alle s in de resolventen verzameling bestaat er een Laurent series ontwikkeling:
Waar Rk weer lineaire, begrensde operatoren op X zijn.
Schrijf nu sI-A = s(I-A/s) en pas een Neumann ontwikkeling toe:
En het volgt al snel dat Rk = Ak-1
Dan volgt het echte vraagstuk:
Bereken:
Nu weten we dat de resolvent geen analytische voortzetting bevat in het spectrum van A, maar complexe functietheorie vertelt ons dat we integraal kunnen evalueren door naar het residu te kijken. Nu weten we niet of het spectrum überhaupt aftelbaar is, dus nu mijn vraag, hoe gebruiken we complexe functietheorie om deze integraal te evalueren?
Merk tevens op dat de resolvent een operator is, en we dus integreren over lineaire operators op X.
Ik weet niet veel van Banachruimten, maar hier zal toch haast wel An uitkomen?
Zolang de straal van C maar groter is dan |A| convergeert de reeks absoluut en kun je integraal en som omwisselen. Maar dan staat het er gewoon.
[ Bericht 25% gewijzigd door thabit op 30-07-2018 21:37:33 ]
Zolang de straal van C maar groter is dan |A| convergeert de reeks absoluut en kun je integraal en som omwisselen. Maar dan staat het er gewoon.
[ Bericht 25% gewijzigd door thabit op 30-07-2018 21:37:33 ]
Want de enige term die een bijdrage levert is k = n+1 (dat levert een integrand A^n / s op) en verder zijn alle residuen 0?quote:Op maandag 30 juli 2018 15:59 schreef thabit het volgende:
Ik weet niet veel van Banachruimten, maar hier zal toch haast wel An uitkomen?
Zolang de straal van C maar groter is dan |A| convergeert de reeks absoluut en kun je integraal en som omwisselen. Maar dan staat het er gewoon.
[ Bericht 0% gewijzigd door #ANONIEM op 30-07-2018 22:32:39 ]
Ja, sk is primitiveerbaar als k niet gelijk is aan -1 en dus is de integraal over een gesloten pad gelijk aan 0.quote:Op maandag 30 juli 2018 22:31 schreef Amoeba het volgende:
[..]
Want de enige term die een bijdrage levert is k = n+1 (dat levert een integrand A^n / s op) en verder zijn alle residuen 0?
OK het probleem is dat ik bij voorbeeld 2 even nergens meer kan vinden hoe je met die exact strepen op wortel vijf keer wortel 25 uitkomt...
Boven de deelstreep is alles appeltje eitje. Er onder is het ineens hub hub barbatruc
Op donderdag 23 mei 2024 23:36 schreef DerRabbit het volgende: Ja oké, daar heb je gelijk in.
Ohww. Ik ben een blonde gans. Dat is de wortel van (1^2+2^2)maal de wortel van (3^2+4^2) natuurlijk... Mijn excuses
Op donderdag 23 mei 2024 23:36 schreef DerRabbit het volgende: Ja oké, daar heb je gelijk in.
Van rechtsboven via rechtsonder naar linksonder lees je A B C D E F G H I J K. Dit patroon is er ook als je twee vakjes meer naar links begint: dan moet er A B C D E F G staan, en dus een E op de plek van het vraagteken.
Aaah ik zie hem, thanks!quote:
Van rechtsboven via rechtsonder naar linksonder lees je A B C D E F G H I J K. Dit patroon is er ook als je twee vakjes meer naar links begint: dan moet er A B C D E F G staan, en dus een E op de plek van het vraagteken.
Nog een
Eerste getal is telkens het kwadraat van het tweede getal, 12 dus.quote:
[..]
Aaah ik zie hem, thanks!
Nog een
[ afbeelding ]
Oh jeetje, ik las het als decimalen. Thanks. : ]quote:
[..]
Eerste getal is telkens het kwadraat van het tweede getal, 12 dus.
Waarom wil je dit eigenlijk doen? Deze vragen komen uit oefenexamens van de overheid in de Australische deelstaat Victoria. Het gaat om toelatingsexamens voor een viertal middelbare scholen (de zogeheten Selective Entry High Schools), en dit zijn oefenexamens die ouders hun kinderen kunnen voorleggen.quote:
[..]
Oh jeetje, ik las het als decimalen. Thanks. : ]
Ahh leuk, kunnen ze mooi trucjes leren.quote:
[..]
Waarom wil je dit eigenlijk doen? Deze vragen komen uit oefenexamens van de overheid in de Australische deelstaat Victoria. Het gaat om toelatingsexamens voor een viertal middelbare scholen (de zogeheten Selective Entry High Schools), en dit zijn oefenexamens die ouders hun kinderen kunnen voorleggen.
Op donderdag 23 mei 2024 23:36 schreef DerRabbit het volgende: Ja oké, daar heb je gelijk in.
Onderstaande grammar is ambigu omdat er twee parse trees van gemaakt kunnen worden:
Zijnde:
Dit komt volgens mij omdat er eerst voor zowel <expr> + <expr> als voor <expr> * <expr> gekozen kan worden?
Echter met onderstaande grammar:
zou dit probleem van ambiguďteit niet bestaan omdat het linker element altijd een <num> is en het rechter deel de <expression>?
Of gaat er iets mis in mijn gedachtegang? De laatste grammar heb ik geschreven a.d.h.v. een eenvoudige javascript vergelijking. En betekent dit dat de grammar onjuist is omdat er een left to right prescedence in zit waardoor de wiskundige voorrang van vermenigvuldigen en delen die wel in Javascript zitten niet gerepresenteerd wordt?
ขอแสดงความนับถือ Flip.
Zijnde:
Dit komt volgens mij omdat er eerst voor zowel <expr> + <expr> als voor <expr> * <expr> gekozen kan worden?
Echter met onderstaande grammar:
zou dit probleem van ambiguďteit niet bestaan omdat het linker element altijd een <num> is en het rechter deel de <expression>?
Of gaat er iets mis in mijn gedachtegang? De laatste grammar heb ik geschreven a.d.h.v. een eenvoudige javascript vergelijking. En betekent dit dat de grammar onjuist is omdat er een left to right prescedence in zit waardoor de wiskundige voorrang van vermenigvuldigen en delen die wel in Javascript zitten niet gerepresenteerd wordt?
ขอแสดงความนับถือ Flip.
I think that it’s extraordinarily important that we in computer science keep fun in computing
For all who deny the struggle, the triumphant overcome
Met zwijgen kruist men de duivel
For all who deny the struggle, the triumphant overcome
Met zwijgen kruist men de duivel
In de tweede grammatica wordt de expressie 2*3+4 als 2*(3+4) geparset.quote:Op zondag 21 oktober 2018 19:26 schreef FlippingCoin het volgende:
Onderstaande grammar is ambigu omdat er twee parse trees van gemaakt kunnen worden:
[ afbeelding ]
Zijnde:
[ afbeelding ]
Dit komt volgens mij omdat er eerst voor zowel <expr> + <expr> als voor <expr> * <expr> gekozen kan worden?
Echter met onderstaande grammar:
[ afbeelding ]
zou dit probleem van ambiguďteit niet bestaan omdat het linker element altijd een <num> is en het rechter deel de <expression>?
Of gaat er iets mis in mijn gedachtegang? De laatste grammar heb ik geschreven a.d.h.v. een eenvoudige javascript vergelijking. En betekent dit dat de grammar onjuist is omdat er een left to right prescedence in zit waardoor de wiskundige voorrang van vermenigvuldigen en delen die wel in Javascript zitten niet gerepresenteerd wordt?
ขอแสดงความนับถือ Flip.
Ja dus met een foutieve parse tree toch?quote:
[..]
In de tweede grammatica wordt de expressie 2*3+4 als 2*(3+4) geparset.
I think that it’s extraordinarily important that we in computer science keep fun in computing
For all who deny the struggle, the triumphant overcome
Met zwijgen kruist men de duivel
For all who deny the struggle, the triumphant overcome
Met zwijgen kruist men de duivel
Niet overeenkomstig de gebruikelijke voorrangsregels voor wiskundige operatoren nee.quote:
[..]
Ja dus met een foutieve parse tree toch?
Oke dankjewel helder.quote:
[..]
Niet overeenkomstig de gebruikelijke voorrangsregels voor wiskundige operatoren nee.
I think that it’s extraordinarily important that we in computer science keep fun in computing
For all who deny the struggle, the triumphant overcome
Met zwijgen kruist men de duivel
For all who deny the struggle, the triumphant overcome
Met zwijgen kruist men de duivel
Een klein vraagje heb ik over het algoritme van Linear Discriminant Analysis. Voor mijn scriptie moet ik dit algoritme kennen en ook kunnen uitleggen uiteindelijk. Echter, ik vind het nog zeer ingewikkeld en kan nergens ook echt een duidelijke uitleg vinden. Op youtube heb ik via dit filmpje een goede uitleg gevonden:
Voor mijn verslag probeer ik het nu algemeen uit te leggen zonder gebruik te maken van een voorbeeld. Zou iemand mij hier aub bij kunnen helpen.
Voor mijn verslag probeer ik het nu algemeen uit te leggen zonder gebruik te maken van een voorbeeld. Zou iemand mij hier aub bij kunnen helpen.
Hi, ik heb een redelijk goeie uitleg gevonden waar in 5 stappen het hele algoritme wordt uitgelegd.: https://sebastianraschka.com/Articles/2014_python_lda.htmlquote:
Een klein vraagje heb ik over het algoritme van Linear Discriminant Analysis. Voor mijn scriptie moet ik dit algoritme kennen en ook kunnen uitleggen uiteindelijk. Echter, ik vind het nog zeer ingewikkeld en kan nergens ook echt een duidelijke uitleg vinden. Op youtube heb ik via dit filmpje een goede uitleg gevonden:
Voor mijn verslag probeer ik het nu algemeen uit te leggen zonder gebruik te maken van een voorbeeld. Zou iemand mij hier aub bij kunnen helpen.
Ik vroeg me alleen af; weet iemand wat wordt bedoeld met deze formule:
Als je in de inhoudsopgave op paragraaf 2.1 klikt dan kom je bij deze formule
De tex-link in de OP is dood.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Wat bedoel je precies? Ik zit niet zo vaak op dit forum, maar als de formule niet te zien is, hier de link:quote:
https://ibb.co/RHS1vY1
Je kan ook op de link waar LDA wordt uitgelegd op 2.1 klikken in de inhoudsopgave
De link naar de uitleg omtrent latex-opmaak in de OP.quote:
[..]
Wat bedoel je precies? Ik zit niet zo vaak op dit forum, maar als de formule niet te zien is, hier de link:
https://ibb.co/RHS1vY1
Je kan ook op de link waar LDA wordt uitgelegd op 2.1 klikken in de inhoudsopgave
-edit: sorry, ging niet over jouw post, maar over de OP (openingspost, helemaal bovenaan).
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Dat is al heel lang zo, geďnteresseerden zouden in plaats daarvan deze blogs (vijf stuks) kunnen doornemen.quote:
Het echte probleem is dat de TeX parser op FOK niet meer werkt sinds de overgang van FOK naar https op 11 december 2018. Wel in oude posts, maar niet in recente posts of in nieuwe posts.
Dus, dit werkt nu niet:
Als alternatief zou je voorlopig gebruik kunnen maken van deze editor om linkjes te genereren naar gifjes van je TeX code die je dan in je berichten op kunt nemen:
Dit is echter erg omslachtig als je een bericht wil schrijven met veel TeX code. Ik heb deze bug al op 12 december j.l. gerapporteerd maar meer dan een maand later is dit nog steeds niet opgelost.
Even een hersenkrakertje.
De vraagstelling:
Zij A een matrix (n x n), Aij = {1,..,n2/2} waarbij iedere waarde precies twee keer voorkomt. Neem verder aan dat n2/2 een geheel getal is én n > 2.
Te bewijzen:
Er bestaat een set X zdd |X| = n en X bestaat uit paren (i,j) zdd dat voor iedere (i,j), (k,l) de volgende beweringen waar zijn:
i =! k
j =! l
Aij =! Akl
Maw X is een set indices zodanig dat de matrix entries niet in dezelfde kolom, niet in dezelfde rij zitten én niet dezelfde waarde delen. Een (triviaal) voorbeeld is dus de diagonaal van de matrix als die niet tweemaal dezelfde waarde bevat.
Mijn poging:
Construeer een graaf G = (V,E) op de matrix waarbij twee punten verbonden zijn als ze in dezelfde kolom of rij zitten óf dezelfde waarde delen. Ieder punt heeft dus (2n-2) of 2n-1 connecties. Merk op dat |V| = n2
Het doel is nu om te bewijzen dat V een 'independent set' bevat van tenminste n punten.. Nou weten we dat er minimaal een independent set is van grootte |V|/(d+1) waarbij d de maximale graad van een punt is, in ons geval is dat 2n-1.. Dit levert zoiets als n/2 op en dat is nog niet goed genoeg...
Iemand een beter idee?
[ Bericht 0% gewijzigd door #ANONIEM op 26-03-2019 16:39:14 ]
De vraagstelling:
Zij A een matrix (n x n), Aij = {1,..,n2/2} waarbij iedere waarde precies twee keer voorkomt. Neem verder aan dat n2/2 een geheel getal is én n > 2.
Te bewijzen:
Er bestaat een set X zdd |X| = n en X bestaat uit paren (i,j) zdd dat voor iedere (i,j), (k,l) de volgende beweringen waar zijn:
i =! k
j =! l
Aij =! Akl
Maw X is een set indices zodanig dat de matrix entries niet in dezelfde kolom, niet in dezelfde rij zitten én niet dezelfde waarde delen. Een (triviaal) voorbeeld is dus de diagonaal van de matrix als die niet tweemaal dezelfde waarde bevat.
Mijn poging:
Construeer een graaf G = (V,E) op de matrix waarbij twee punten verbonden zijn als ze in dezelfde kolom of rij zitten óf dezelfde waarde delen. Ieder punt heeft dus (2n-2) of 2n-1 connecties. Merk op dat |V| = n2
Het doel is nu om te bewijzen dat V een 'independent set' bevat van tenminste n punten.. Nou weten we dat er minimaal een independent set is van grootte |V|/(d+1) waarbij d de maximale graad van een punt is, in ons geval is dat 2n-1.. Dit levert zoiets als n/2 op en dat is nog niet goed genoeg...
Iemand een beter idee?
[ Bericht 0% gewijzigd door #ANONIEM op 26-03-2019 16:39:14 ]
|
|
