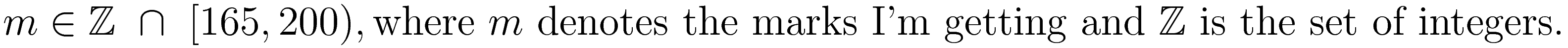SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Gegeven is:
max w(K,L) = 12K -1/2 L 1/4 - 1,2K - 0,6L
En ik moet de 'mogelijke oplossing vinden voor de volgende speciale case''.
Partieel afgeleide naar k is 6K -1/2 L 1/4 - 1,2 = 0 en partieel afgeleide naar L is:
3K 1/2 L -3/4 - 0,6 = 0
Dus:
K -1/2 L 1/4 = K 1/2 L -3/4 = 1/5 = 0,2
Maar wat moet ik daarna doen?
max w(K,L) = 12K -1/2 L 1/4 - 1,2K - 0,6L
En ik moet de 'mogelijke oplossing vinden voor de volgende speciale case''.
Partieel afgeleide naar k is 6K -1/2 L 1/4 - 1,2 = 0 en partieel afgeleide naar L is:
3K 1/2 L -3/4 - 0,6 = 0
Dus:
K -1/2 L 1/4 = K 1/2 L -3/4 = 1/5 = 0,2
Maar wat moet ik daarna doen?
Ik heb de volgende winstfunctie:
-2x² - 4y² + 4xy + 64x + 32y - 514 en ik moet de stationaire punten berekenen en dat doe ik door de afgeleide van de twee variabelen te nemen en te kijken wanneer deze 0 is:
f'x = -4x + 4y + 64
f'y = -8y + 4x + 32
Hoe kan ik dan de stationaire punten bepalen (kijken wanneer f'x = 0 en f'y = 0) als er twee variabelen zitten in beide afgeleiden?
-2x² - 4y² + 4xy + 64x + 32y - 514 en ik moet de stationaire punten berekenen en dat doe ik door de afgeleide van de twee variabelen te nemen en te kijken wanneer deze 0 is:
f'x = -4x + 4y + 64
f'y = -8y + 4x + 32
Hoe kan ik dan de stationaire punten bepalen (kijken wanneer f'x = 0 en f'y = 0) als er twee variabelen zitten in beide afgeleiden?
Je hebt hier een uitdrukking die afhangt van twee variabelen x en y en daarmee een functiequote:Op vrijdag 17 oktober 2014 12:01 schreef Super-B het volgende:
Ik heb de volgende winstfunctie:
-2x² - 4y² + 4xy + 64x + 32y - 514 en ik moet de stationaire punten berekenen en dat doe ik door de afgeleide van de twee variabelen te nemen en te kijken wanneer deze 0 is:
f'x = -4x + 4y + 64
f'y = -8y + 4x + 32
Hoe kan ik dan de stationaire punten bepalen (kijken wanneer f'x = 0 en f'y = 0) als er twee variabelen zitten in beide afgeleiden?
Als we nu de afhankelijke variabele, oftewel de functiewaarde, even z noemen, dus
dan is dus
In een driedimensionaal cartesisch assenstelsel is dit een vergelijking van een gekromd oppervlak dat een hoogste punt bezit zoals je hier kunt zien, en het gaat nu om de bepaling van de coördinaten van het hoogste punt op dit gekromde oppervlak.
Als we dit gekromde oppervlak snijden met een plat vlak loodrecht op de x-as, dus een vlak met de vergelijking x = a, waarin a een constante is, dan krijgen we in dat platte vlak een curve als snijlijn met ons gekromde vlak, en datzelfde geldt uiteraard wanneer we het gekromde oppervlak snijden met een plat vlak loodrecht op de y-as, dus een vlak met vergelijking y = b, waarin b weer een constante is. Als we nu die constantes a en b zo weten te kiezen dat het hoogste punt op het gekromde oppervlak in beide snijvlakken ligt, dan is het hoogste punt van het gekromde oppervlak dus ook het hoogste punt op elk van deze beide snijcurves. En dat betekent dat de afgeleide van f(x, y) naar x als we y constant houden nul moet zijn en tevens dat de afgeleide van f(x, y) naar y als we x constant houden nul moet zijn. We krijgen als voorwaarden dus
Of, omdat we de afhankelijke variabele z hebben genoemd
De gekrulde ∂ (in het Engels: curly dee) wordt hier gebruikt om aan te geven dat we met partiële afgeleiden te doen hebben, waarbij we dus kijken hoe een afhankelijke variabele (hier: z) die afhangt van meerdere onafhankelijke variabelen (hier: x en y) varieert als we slechts één variabele laten veranderen en de overige variabelen even constant houden. De partiële afgeleiden van je functie had je al correct bepaald, en de voorwaarden dat deze beide gelijktijdig nul moeten zijn geven dus het volgende stelsel vergelijkingen in x en y:
Nu moet je dit stelsel oplossen. Het is een lineair stelsel, en je hebt al eerder lineaire stelsels opgelost, dus dit zou geen probleem meer mogen zijn. Als we de linkerleden en de rechterleden van deze twee vergelijkingen bij elkaar optellen, dan krijgen we
en dus
en invullen van deze waarde van y in één van de beide oorspronkelijke vergelijkingen geeft dan
en het maximum van de functie is dus
De coördinaten van het hoogste punt op het gekromde oppervlak met als vergelijking z = f(x, y) zijn dus (40, 24, 1150).
[ Bericht 0% gewijzigd door Riparius op 18-10-2014 18:04:34 ]
''En dat betekent dat de afgeleide van f(x, y) naar x als we y constant houden nul moet zijn en tevens dat de afgeleide van f(x, y) naar y als we x constant houden nul moet zijn.''quote:
En dat betekent dat de afgeleide van f(x, y) naar x als we y constant houden nul moet zijn en tevens dat de afgeleide van f(x, y) naar y als we x constant houden nul moet zijn. We krijgen als voorwaarden dus
Scherp. Bedankt.
Hoi Riparius, ik heb nog één vraagje:quote:
g(x,y) = xye4x² -5xy + y²
Dit is de methode die er gebruikt wordt om de stationaire punten te bepalen:
Echter vraag ik mij af hoe ze tot √2 en -√2 komen als y coördinaat op het einde.. en hoe je dat zonder rekenmachine kunt uitrekenen... (?)
Alvast enorm bedankt.
Wel, ze vindenquote:
[..]
Hoi Riparius, ik heb nog één vraagje:
g(x,y) = xye4x² -5xy + y²
Dit is de methode die er gebruikt wordt om de stationaire punten te bepalen:
[ afbeelding ]
Echter vraag ik mij af hoe ze tot √2 en -√2 komen als y coördinaat op het einde.. en hoe je dat zonder rekenmachine kunt uitrekenen... (?)
Alvast enorm bedankt.
en dit geeft
en dus
Maar nu is
zodat we hebben
en dit mag je verder zo laten staan. Er zijn manieren om vierkantswortels met pen en papier te berekenen (benaderen) in ieder gewenst aantal decimalen, maar dat wordt hier niet gevraagd.
Ja dat klopt. Bedankt.quote:
[..]
Wel, ze vinden
en dit geeft
en dus
Maar nu is
zodat we hebben
en dit mag je verder zo laten staan. Er zijn manieren om vierkantswortels met pen en papier te berekenen (benaderen) in ieder gewenst aantal decimalen, maar dat wordt hier niet gevraagd.
Maar ik bedoelde het y-coördinaat.
Weet iemand hoe
(ex+y + ex-y )² - (ex+y + ex-y )²
te calculeren is?
Moet ik het eerst helemaal uitschrijven? Zo ja, hoe moet ik dat doen? Ik zou dan eerst het linkerterm moeten vermenigvuldigen:
(ex+y + ex-y ) * (ex+y + ex-y )
Maar hoe moet ik dit vermenigvuldigen?
Bij voorbaat dank.
(ex+y + ex-y )² - (ex+y + ex-y )²
te calculeren is?
Moet ik het eerst helemaal uitschrijven? Zo ja, hoe moet ik dat doen? Ik zou dan eerst het linkerterm moeten vermenigvuldigen:
(ex+y + ex-y ) * (ex+y + ex-y )
Maar hoe moet ik dit vermenigvuldigen?
Bij voorbaat dank.
Dat is heel eenvoudig: ze hadden namelijk ook gevonden dat y = 2x, dus de bijbehorende y-coördinaten worden dan √2 resp. −√2.quote:
[..]
Ja dat klopt. Bedankt.
Maar ik bedoelde de y-coördinaat.
Sleutelwoord: merkwaardige producten. Hoe vaak heb ik je al gezegd dat je deze van buiten moet kennen én ook altijd moet herkennen?quote:
Weet iemand hoe
(ex+y + ex-y )² - (ex+y + ex-y )²
te calculeren is?
Moet ik het eerst helemaal uitschrijven? Zo ja, hoe moet ik dat doen? Ik zou dan eerst het linkerterm moeten vermenigvuldigen:
(ex+y + ex-y ) * (ex+y + ex-y )
Maar hoe moet ik dit vermenigvuldigen?
Bij voorbaat dank.
Hier heb je een verschil van twee kwadraten, dus maak je gebruik van
Ik zou trouwens als ik jou was eerst eens even goed kijken of je de opgave wel correct hebt overgenomen. Zie je ook waarom?
Maar dan zit ik er alsnog mee hoe ik het moet vermenigvuldigen omdat er al exponenten staan e.d....quote:
[..]
Sleutelwoord: merkwaardige producten. Hoe vaak heb ik je al gezegd dat je deze van buiten moet kennen én ook altijd moet herkennen?
Hier heb je een verschil van twee kwadraten, dus maak je gebruik van
(ex+y - ex-y ) * (ex+y + ex-y )
Is hier overigens geen sprake van a² - a², aangezien er hetzelfde staat tussen beide haakjes?quote:
[..]
Sleutelwoord: merkwaardige producten. Hoe vaak heb ik je al gezegd dat je deze van buiten moet kennen én ook altijd moet herkennen?
Hier heb je een verschil van twee kwadraten, dus maak je gebruik van
Ik zou trouwens als ik jou was eerst eens even goed kijken of je de opgave wel correct hebt overgenomen. Zie je ook waarom?
Ga nu eerst die opgave nog eens heel goed controleren, want de uitdrukking die je geeft is gewoon gelijk aan nul, en dat lijkt me niet de bedoeling.quote:
[..]
Maar dan zit ik er alsnog mee hoe ik het moet vermenigvuldigen omdat er al exponenten staan e.d....
(ex+y - ex-y ) * (ex+y + ex-y )
Exact. En daarom staat er gewoon nul. Maar controleer de opgave.quote:
[..]
Is hier overigens geen sprake van a² - a², aangezien er hetzelfde staat tussen beide haakjes?
In het antwoordenboek staat er: 4ex+y e x-yquote:
[..]
Exact. En daarom staat er gewoon nul. Maar controleer de opgave.
Duidelijk. Hartstikke bedankt.quote:
[..]
Dat is heel eenvoudig: ze hadden namelijk ook gevonden dat y = 2x, dus de bijbehorende y-coördinaten worden dan √2 resp. −√2.
Hier heb ik nog een vreselijke opgave:
f(x,y) = x² - y² - xy - x³
''find the domain S where f is concave and find the largest value f in S''
Ik kwam inderdaad uit op x > 1/3, maar ik heb geen flauw benul hoe ze op x > 5/12 komen.
Ik weet natuurlijk wel dat als je x > 1/3 en x > 5/12 hebt, dat uiteindelijk x > 5/12 gewoon geldt.
En nu wil je dat ik in mijn glazen bol kijk om te zien wat de correcte bijbehorende opgave moet zijn?quote:
[..]
In het antwoordenboek staat er: 4ex+y e x-y
Nou je boft, want mijn glazen bol doet het. Je opgave is
Zie je het verschil met wat je zelf hebt gepost?
Dom en stom van me.quote:
[..]
En nu wil je dat ik in mijn glazen bol kijk om te zien wat de correcte bijbehorende opgave moet zijn?
Nou je boft, want mijn glazen bol doet het. Je opgave is
Zie je het verschil met wat je zelf hebt gepost?
Dan zou ik zeggen dat e x + y = a
e x - y = b
dus:
(a + b)² - (a - b)²
en dan dus:
a² + b² - a² - b²
a² - a² + b² + b²
0 + 2b² ?
Niet x > 5/12 maar x ≥ 5/12. Dit is heel eenvoudig: de tweede ongelijkheid in x die ze vinden geeftquote:
[..]
Duidelijk. Hartstikke bedankt.
Hier heb ik nog een vreselijke opgave:
f(x,y) = x² - y² - xy - x³
''find the domain S where f is concave and find the largest value f in S''
[ afbeelding ]
Ik kwam inderdaad uit op x > 1/3, maar ik heb geen flauw benul hoe ze op x > 5/12 komen.
Ik weet natuurlijk wel dat als je x > 1/3 en x > 5/12 hebt, dat uiteindelijk x > 5/12 gewoon geldt.
−4 + 12x − 1 ≥ 0
12x ≥ 5
x ≥ 5/12
Nee. Wat jij wil kan ook, maar dan moet je gebruik maken van de identiteitquote:
[..]
Dom en stom van me.
Dan zou ik zeggen dat e x + y = a
e x - y = b
dus:
(a + b)² - (a - b)²
en dan dus:
a² + b² - a² - b²
a² - a² + b² + b²
0 + 2b² ?
die in Frankrijk wel de identiteit van Legendre wordt genoemd maar die in de rest van de wereld geen aparte naam heeft.
Wat ik bedoelde was dat je de eerste uitdrukking tussen haakjes gelijk stelt aan a en de tweede uitdrukking tussen haakjes gelijk stelt aan b.
En leer nu eens die merkwaardige producten. Het kwadraat van een som of verschil van twee grootheden is niet gelijk aan de som resp. het verschil van de kwadraten van die grootheden, want we hebben
Als je de leden van de tweede van deze identiteiten aftrekt van de leden van de eerste van deze identiteiten dan krijg je bovenstaande identiteit
Deze identiteit kunnen we ook heel fraai visualiseren. Veronderstel dat a en b positieve getallen zijn met a > b, dan is (a+b)² de oppervlakte van een vierkant met zijde a+b terwijl (a−b)² dan de oppervlakte is van een kleiner vierkant met zijde a−b. Het verschil van de oppervlaktes van deze vierkanten is gelijk aan de oppervlakte van vier rechthoeken met lengte a en breedte b, en dat betekent dat we met deze vier rechthoeken en het vierkant met zijde a−b een groter vierkant met zijde a+b kunnen vormen:
Je ziet nu waarom jouw herleiding niet klopt.
[ Bericht 5% gewijzigd door Riparius op 17-10-2014 20:35:55 ]
Top!quote:
[..]
Niet x > 5/12 maar x ≥ 5/12. Dit is heel eenvoudig: de tweede ongelijkheid in x die ze vinden geeft
−4 + 12x − 1 ≥ 0
12x ≥ 5
x ≥ 5/12
[ Bericht 8% gewijzigd door Super-B op 17-10-2014 17:03:01 ]
max 10x1/2 y 1/3 subject to 2x + 4y = m
Ik kom hier echt helemaal niet uit met de lagrange functie door de exponenten..
Ik heb:
L = 10x1/2 y 1/3 - T(2x + 4y - m)
L'x = 5x-1/2 y 1/3 - 2T
L'y = 10/3-1/3 - 4T
En dan loop ik vast.. Kan iemand mij alsjeblieft helpen?
Ik kom hier echt helemaal niet uit met de lagrange functie door de exponenten..
Ik heb:
L = 10x1/2 y 1/3 - T(2x + 4y - m)
L'x = 5x-1/2 y 1/3 - 2T
L'y = 10/3-1/3 - 4T
En dan loop ik vast.. Kan iemand mij alsjeblieft helpen?
Er zit een fout in je uitdrukking voor ∂L/∂y. Je moet ook L nog naar T differentiëren en dan heb je ∂L/∂T = 2x + 4y − m. Alle drie de partiële afgeleiden stel je gelijk aan nul, en dat geeft een stelsel van drie vergelijkingen in de drie onbekenden x, y, T terwijl m een parameter is. Dit stelsel ga je dan oplossen.quote:
max 10x1/2 y 1/3 subject to 2x + 4y = m
Ik kom hier echt helemaal niet uit met de lagrange functie door de exponenten..
Ik heb:
L = 10x1/2 y 1/3 - T(2x + 4y - m)
L'x = 5x-1/2 y 1/3 - 2T
L'y = 10/3-1/3 - 4T
En dan loop ik vast.. Kan iemand mij alsjeblieft helpen?
Oeps sorry. Ik was er vergeten bij te zetten dat T = lambda.quote:
[..]
Er zit een fout in je uitdrukking voor ∂L/∂y. Je moet ook L nog naar T differentiëren en dan heb je ∂L/∂T = 2x + 4y − m. Alle drie de partiële afgeleiden stel je gelijk aan nul, en dat geeft een stelsel van drie vergelijkingen in de drie onbekenden x, y, T terwijl m een parameter is. Dit stelsel ga je dan oplossen.
Ik vind het lastig, omdat dit een cobb-douglas functie is met ook nog eens met exponenten met een deling.
Die voorwaarden kloppen niet helemaal die in dat modelantwoord staan.quote:
[..]
Duidelijk. Hartstikke bedankt.
Hier heb ik nog een vreselijke opgave:
f(x,y) = x² - y² - xy - x³
''find the domain S where f is concave and find the largest value f in S''
[ afbeelding ]
Ik kwam inderdaad uit op x > 1/3, maar ik heb geen flauw benul hoe ze op x > 5/12 komen.
Ik weet natuurlijk wel dat als je x > 1/3 en x > 5/12 hebt, dat uiteindelijk x > 5/12 gewoon geldt.
In plaats van
Edit: dat maakt in dit specifieke geval niet uit zie ik, als det >= 0, dan is het equivalent.
Die T moet een lambda zijn he..quote:
[..]
Er zit een fout in je uitdrukking voor ∂L/∂y. Je moet ook L nog naar T differentiëren en dan heb je ∂L/∂T = 2x + 4y − m. Alle drie de partiële afgeleiden stel je gelijk aan nul, en dat geeft een stelsel van drie vergelijkingen in de drie onbekenden x, y, T terwijl m een parameter is. Dit stelsel ga je dan oplossen.
Ben er overigens nog steeds niet uitgekomen.
Dan moet je een λ schrijven. Die kun je (bijvoorbeeld) krijgen doorquote:
te typen.
Ga het nu toch maar zelf proberen. Als je die m lastig vindt, werk het dan eerst eens uit met een concrete waarde voor m, bijvoorbeeld m = 10, dan heb je dit.quote:Ben er overigens nog steeds niet uitgekomen.
Hello,
''2y = [2x / (2x+ y) ] * (x + 2y)
ook wel y² = x² ''
Hoe kun je het in der mate 'oplossen' dat er y² = x² uitrolt?
''2y = [2x / (2x+ y) ] * (x + 2y)
ook wel y² = x² ''
Hoe kun je het in der mate 'oplossen' dat er y² = x² uitrolt?
Vermenigvuldig beide leden met (2x + y) en je hebtquote:
Hello,
''2y = [2x / (2x+ y) ] * (x + 2y)
ook wel y² = x² ''
Hoe kun je het in der mate 'oplossen' dat er y² = x² uitrolt?
2y(2x + y) = 2x(x + 2y)
Zie je het nu?
Yes. Thankyou.quote:
[..]
Vermenigvuldig beide leden met (2x + y) en je hebt
2y(2x + y) = 2x(x + 2y)
Zie je het nu?
Kan je mij met nog iets helpen?quote:
[..]
Vermenigvuldig beide leden met (2x + y) en je hebt
2y(2x + y) = 2x(x + 2y)
Zie je het nu?
max(min) 3xy subject to x² + y² = 8:
Ik kom op dezelfde x-coordinaten uit, maar hoe worden de y coördinaten en lambda berekend??
Je komt uit op het stelselquote:
[..]
Kan je mij met nog iets helpen?
max(min) 3xy subject to x² + y² = 8:
[ afbeelding ]
Ik kom op dezelfde x-coordinaten uit, maar hoe worden de y coördinaten en lambda berekend??
x² + y² = 8
x² = y²
en dit heeft de vier geordende paren (2, 2), (−2, −2), (2, −2), (−2, 2) als oplossingen aangezien x en y elk zowel +2 als −2 kunnen zijn. Dan substitueer je elk van deze vier paren in één van de betrekkingen ( i ) 3y = 2λx of ( ii ) 3x = 2λy en dan vind je λ = 3/2 voor de geordende paren (2, 2) en (−2, −2) en λ = −3/2 voor de geordende paren (2, −2) en (−2, 2).
Hoe kan ik y vinden als ik
1/(2+x^2) wil invullen in x^2 + 2y = 2
Na het invullen kan ik de x niet wegwerken, doordat er een 2 + in de noemer staat..
1/(2+x^2) wil invullen in x^2 + 2y = 2
Na het invullen kan ik de x niet wegwerken, doordat er een 2 + in de noemer staat..
Hoe komen ze hier op de x = 3y ? Ik weet wel hoe ze op die breuk met lambda komen. Daarnaast vraag ik mij af hoe je die lambda elimineert? Want er staat ''Eliminating λ from ( i ) and (ii) we get...''
Hoe doe je dat?
Hoe doe je dat?
Waar wil je het invullen dan?quote:
Hoe kan ik y vinden als ik
1/(2+x^2) wil invullen in x^2 + 2y = 2
Na het invullen kan ik de x niet wegwerken, doordat er een 2 + in de noemer staat..
1/(2+x^2), is geen vergelijking.
-
[ Bericht 99% gewijzigd door Janneke141 op 18-10-2014 12:15:28 ]
[ Bericht 99% gewijzigd door Janneke141 op 18-10-2014 12:15:28 ]
Opinion is the medium between knowledge and ignorance (Plato)
Excuus. Ik tikte het snel via mijn mobiel en was het vergeten.quote:
[..]
Echt hoe vaak is er nou gezegd dat je niet zomaar een = moet weg laten?
Wat wil je nu precies weten? De substitutie is niet bar ingewikkeld. De vraag die je eerder stelde 'hoe vind je y' is hier niet van toepassing - dus waar zit je probleem?quote:
[..]
Excuus. Ik tikte het snel via mijn mobiel en was het vergeten.
Opinion is the medium between knowledge and ignorance (Plato)
Verkeerde plaatje gekopieerd via puush...quote:
[..]
Wat wil je nu precies weten? De substitutie is niet bar ingewikkeld. De vraag die je eerder stelde 'hoe vind je y' is hier niet van toepassing - dus waar zit je probleem?
Op het moment dat jij de tijd er niet voor neemt om het probleem goed op te schrijven, waarom denk je dat wij er dan wel de tijd voor nemen om de vraag goed op te lossen?quote:
[..]
Excuus. Ik tikte het snel via mijn mobiel en was het vergeten.
Het probleem van het volgende probleem zit hem in het invullen van y.. Met name omdat het letters zijn, zie ik door de bomen het bos niet meer.. Ik weet hoe ik op y moet komen, dat is mij gelukt, maar ik weet niet waar ik het moet invullen en hoe ik het moet doen, want door al die breuken en letters.... zie ik de bomen niet meer.quote:
[..]
Op het moment dat jij de tijd er niet voor neemt om het probleem goed op te schrijven, waarom denk je dat wij er dan wel de tijd voor nemen om de vraag goed op te lossen?
Je zoekt de locatie (x- en y-coördinaat) van de top van een of ander gebergte, een gebergte dat is gegeven een functievoorschrift. In dat functievoorschrift zijn x en y de variabelen, en p en q constanten, gewoon getalletjes dus.quote:
[..]
Het probleem van het volgende probleem zit hem in het invullen van y.. Met name omdat het letters zijn, zie ik door de bomen het bos niet meer.. Ik weet hoe ik op y moet komen, dat is mij gelukt, maar ik weet niet waar ik het moet invullen en hoe ik het moet doen, want door al die breuken en letters.... zie ik de bomen niet meer.
[ afbeelding ]
Tot zo ver helder?
Dan ga je, om het maximum te vinden, differentiëren naar x en naar y en beide partiële afgeleiden stel je gelijk aan 0; immers - zo bepaal je een maximum. Beide vergelijkingen leveren een verzameling oplossingen voor x die afhangen van y, in dit geval twee rechte lijnen. Als die beide verzamelingen een of meer gemeenschappelijke punten hebben, dan liggen daar bergtoppen in ons gebergte.
Om dat na te gaan wordt de y-waarde van het snijpunt van die twee lijnen bepaald door de x-waarden aan elkaar gelijk te stellen (Je weet dat, op het punt dat we zoeken, x = ½p-½y-½ én x = q-2y-1, dus er moet wel gelden dat ½p-½y-½ = q-2y-1)
Het oplossen van die vergelijking levert een y-waarde op van dat snijpunt. Als je dat goed hebt gedaan, dan moet wel gelden dat invullen in eender welke vergelijking, dezelfde waarde van x oplevert. We hadden immers het snijpunt gevonden!
Opinion is the medium between knowledge and ignorance (Plato)
Hoe los ik dit verder op? Ik heb werkelijk geen idee wat ik moet doen. Het eindantwoord moet dit zijn:
Gaat om de time evolution van een netwerk. t is de tijd, k is een node en m is het aantal nieuwe links tussen een nieuwe node en het bestaande netwerk.
Hulp zou erg welkom zijn.
Smile like you mean it
www.wefut.com
www.wefut.com
Is die i een index?quote:
[ afbeelding ]
Hoe los ik dit verder op? Ik heb werkelijk geen idee wat ik moet doen. Het eindantwoord moet dit zijn:
[ afbeelding ]
Gaat om de time evolution van een netwerk. t is de tijd, k is een node en m is het aantal nieuwe links tussen een nieuwe node en het bestaande netwerk.
Hulp zou erg welkom zijn.
Ik zou beginnen door links en rechts te integreren.quote:
[ afbeelding ]
Hoe los ik dit verder op? Ik heb werkelijk geen idee wat ik moet doen. Het eindantwoord moet dit zijn:
[ afbeelding ]
Gaat om de time evolution van een netwerk. t is de tijd, k is een node en m is het aantal nieuwe links tussen een nieuwe node en het bestaande netwerk.
Hulp zou erg welkom zijn.
Dankje. Het zijn echt van die kleine dingen waar ik de fout in ga...quote:
[..]
Je zoekt de locatie (x- en y-coördinaat) van de top van een of ander gebergte, een gebergte dat is gegeven een functievoorschrift. In dat functievoorschrift zijn x en y de variabelen, en p en q constanten, gewoon getalletjes dus.
Tot zo ver helder?
Dan ga je, om het maximum te vinden, differentiëren naar x en naar y en beide partiële afgeleiden stel je gelijk aan 0; immers - zo bepaal je een maximum. Beide vergelijkingen leveren een verzameling oplossingen voor x die afhangen van y, in dit geval twee rechte lijnen. Als die beide verzamelingen een of meer gemeenschappelijke punten hebben, dan liggen daar bergtoppen in ons gebergte.
Om dat na te gaan wordt de y-waarde van het snijpunt van die twee lijnen bepaald door de x-waarden aan elkaar gelijk te stellen (Je weet dat, op het punt dat we zoeken, x = ½p-½y-½ én x = q-2y-1, dus er moet wel gelden dat ½p-½y-½ = q-2y-1)
Het oplossen van die vergelijking levert een y-waarde op van dat snijpunt. Als je dat goed hebt gedaan, dan moet wel gelden dat invullen in eender welke vergelijking, dezelfde waarde van x oplevert. We hadden immers het snijpunt gevonden!
Zoals het volgende:
x² = 81 --> x = 9 of -9
Dat snap ik maar dan staat er:
Since the Lagrangian is concave, the solution is at x = 9 , y = 12 with lambda = 1/6
De formule is:
max f(x,y) = 3x + 4y subject to g(x,y) = x² + y² = 225
Omdat er een max staat is het concave volgens mij (?), maar hoezo is de oplossing alleen bij x = 9? Bij x = -9 rolt er toch ook gewoon y = 12 uit..?
-9² + y² = 225
y² = 225 - 81
y² = 144
y = 12.
Ja, zo ver kwam ik ook. Maar ik weet dus al niet hoe dat moet.quote:
[..]
Ik zou beginnen door links en rechts te integreren.
Vandaar mijn roep om hulp.
Smile like you mean it
www.wefut.com
www.wefut.com
Je weet niet hoe je dx/x, ofwel (1/x)dx moet integreren?quote:
[..]
Ja, zo ver kwam ik ook. Maar ik weet dus al niet hoe dat moet.
Ik moet erkennen dat dat inderdaad aardig ver is weggezakt. Al kan ik mij ook alleen maar heugen dat ik geïntegreerd heb met de GR.quote:
[..]
Je weet niet hoe je dx/x, ofwel (1/x)dx moet integreren?
Zeker, al weet ik dan nog niet echt hoe ik tot het eindantwoord kom. Dat is overigens van deze vorm (klopte niet helemaal in mijn originele post):quote:
Wat is nu mijn vervolgstap?
Smile like you mean it
www.wefut.com
www.wefut.com
Dan raad ik je aan om dat eerst eens goed te bestuderen alvorens met dit probleem verder te gaan.quote:
[..]
Ik moet erkennen dat dat inderdaad aardig ver is weggezakt. Al kan ik mij ook alleen maar heugen dat ik geïntegreerd heb met de GR.
Zoals al vaker hier is gezegd...quote:
[ afbeelding ]
Hoe los ik dit verder op? Ik heb werkelijk geen idee wat ik moet doen. Het eindantwoord moet dit zijn:
[ afbeelding ]
Dit is geen vergelijking, wat stelt het voor?
Als iets een vergelijking is, laat dan niet zomaar de ene helft weg. Wat daar kan je dan niks meer mee.
Ik had mezelf al hersteld.quote:
[..]
Zoals al vaker hier is gezegd...
[ afbeelding ]
Dit is geen vergelijking, wat stelt het voor?
Als iets een vergelijking is, laat dan niet zomaar de ene helft weg. Wat daar kan je dan niks meer mee.
Zie twee posts hierboven
Smile like you mean it
www.wefut.com
www.wefut.com
''Beschouw het probleem:
max xy + 3x subject 2ln(2x+y) = 0
uit g(x) = 2ln(2x+y) is het volgende af te leiden:
2ln(2x+y) = 0
ln ( 2x + y) = 0
2x + y = e0
2x + y = 1
Weet iemand waarom die 2 van 2ln weg mag?
max xy + 3x subject 2ln(2x+y) = 0
uit g(x) = 2ln(2x+y) is het volgende af te leiden:
2ln(2x+y) = 0
ln ( 2x + y) = 0
2x + y = e0
2x + y = 1
Weet iemand waarom die 2 van 2ln weg mag?
Hij heeft net hierboven al een verbeterde uitdrukking gepost als oplossing van zijn DV. En die oplossing staat kennelijk in zijn antwoordenboekje. Dan ga je je inderdaad afvragen hoe het toch mogelijk is dat iemand die hulp verwacht bij een vraagstuk vaak in eerste instantie niet eens de moeite neemt om een vraagstuk correct over te nemen of correct in eigen bewoordingen te presenteren. Los daarvan valt het mij vaak op dat de proliferatie van antwoordenboekjes ertoe heeft geleid dat veel vragenstellers zo geobsedeerd zijn met 'het antwoord' dat ze vergeten dat daar ook nog een correcte vraagstelling bij hoort. Het is sowieso bevreemdend dat doorgaans 'het antwoord' gelijk wordt meegepost. Dat is alsof de vragenstellers in de waan verkeren dat het vraagstuk niet is op te lossen zonder op voorhand het antwoord te kennen. En niet zelden zijn de geposte antwoorden c.q. de in die antwoordenboekjes afgedrukte antwoorden ook nog eens fout, wat dan steevast aanleiding geeft tot een hoop heen en weer gepraat, wantrouwen bij de vragensteller inzake de competentie van de beantwoorder, en tijdverlies door pogingen van de vragensteller om foutieve antwoorden te reproduceren, tijd die veel nuttiger had kunnen worden besteed door echt iets te leren.quote:
[..]
Zoals al vaker hier is gezegd...
[ afbeelding ]
Dit is geen vergelijking, wat stelt het voor?
Als iets een vergelijking is, laat dan niet zomaar de ene helft weg. Wat daar kan je dan niks meer mee.
Omdat je in een vergelijking links en rechts door 2 mag delen?quote:
Weet iemand waarom die 2 van 2ln weg mag?
Opinion is the medium between knowledge and ignorance (Plato)
Ja omdat er een 0 staat na de = teken, vandaar dat ik dacht dat dat niet mocht.quote:
[..]
Omdat je in een vergelijking links en rechts door 2 mag delen?
Au. Kun je uitleggen waarom je dat dacht?quote:
[..]
Ja omdat er een 0 staat na de = teken, vandaar dat ik dacht dat dat niet mocht.
Opinion is the medium between knowledge and ignorance (Plato)
Opzich begrijp ik zijn denkstap wel: het is ook niet mogelijk om beide kanten door 2ln(2x+y) te delen, want dan krijg je 1 = 0. Waarom dit niet mag, vraag ik me eigenlijk ook af.quote:
[..]
Au. Kun je uitleggen waarom je dat dacht?
Als je die vergelijking hebt, wat weet je dan van de waarde van ln(2x+y)? Waarom krijg je dan 1=0 als je door ln(2x+y) deelt?quote:
[..]
Opzich begrijp ik zijn denkstap wel: het is ook niet mogelijk om beide kanten door 2ln(2x+y) te delen, want dan krijg je 1 = 0. Waarom dit niet mag, vraag ik me eigenlijk ook af.
Er is maar één voorwaarde voor het aan beide kanten delen. Die voorwaarde is dat de noemer niet nul mag zijn. Aangezien 2 niet gelijk aan 0 is, mag je hier altijd door delen. Bij ln(2x+y) ligt dit net iets anders. Je zoekt hier namelijk precies de waarden voor x en y waarvoor ln(2x+y) nul is. Als je hier vervolgens door deelt krijg je 0/0. Dat is niet 1, maar het is ongedefinieerd.quote:
[..]
Opzich begrijp ik zijn denkstap wel: het is ook niet mogelijk om beide kanten door 2ln(2x+y) te delen, want dan krijg je 1 = 0. Waarom dit niet mag, vraag ik me eigenlijk ook af.
Omdat, in tegenstelling tot een getal ongelijk aan 0, 2ln(2x+y) best wel eens 0 zou kunnen zijn. En delen door nul is flauwekul, zo is mij verteld.quote:
[..]
Opzich begrijp ik zijn denkstap wel: het is ook niet mogelijk om beide kanten door 2ln(2x+y) te delen, want dan krijg je 1 = 0. Waarom dit niet mag, vraag ik me eigenlijk ook af.
Om het even in een eenvoudiger voorbeeldje te vangen kijken we naar de vergelijking 2x - 6 = 0
Als we de denkfout van Rust zouden volgen, dan mogen we niet links en rechts delen door 2. Ik hoop maar dat ik wel links en rechts 6 mag optellen, en dan staat er 2x = 6. Mag ik nu wel door 2 delen links en rechts? Dan staat er namelijk x = 3, wat precies hetzelfde is als x - 3 = 0.
Waar het op neerkomt is dit: Ik weet dat twee maal "iets" gelijk is aan 0. Het kan dus niet anders, of "iets" moet zelf gelijk aan nul zijn.
Mijn advies is om daarom niet te onthouden wat er wel of niet zou mogen, maar te beredeneren of het mag. Uit het regeltje hierboven, of het triviale voorbeeld, zie je meteen dat het moet mogen. Dit gaat op voor veel meer rekenregels.
En dan naar de 'denkfout' van netchip: als ik in hetzelfde voorbeeld van hierboven op wil lossen 2x - 6 = 0 en ik zou links en rechts mogen delen door 2x-6, dan staat er inderdaad 1 = 0, oftewel een vergelijking zonder oplossingen. Ik heb gedeeld door iets dat wel eens gelijk aan 0 kan zijn, namelijk als x=3. Laat dat nu precies de oplossing van mijn oorspronkelijke vergelijking zijn...
Opinion is the medium between knowledge and ignorance (Plato)
2ln(2x+y) moet gelijk aan nul zijn. Ik bedoelde eigenlijkquote:
[..]
Als je die vergelijking hebt, wat weet je dan van de waarde van ln(2x+y)? Waarom krijg je dan 1=0 als je door ln(2x+y) deelt?
Waarom krijg je dan 0/0?quote:
[..]
Er is maar één voorwaarde voor het aan beide kanten delen. Die voorwaarde is dat de noemer niet nul mag zijn. Aangezien 2 niet gelijk aan 0 is, mag je hier altijd door delen. Bij ln(2x+y) ligt dit net iets anders. Je zoekt hier namelijk precies de waarden voor x en y waarvoor ln(2x+y) nul is. Als je hier vervolgens door deelt krijg je 0/0. Dat is niet 1, maar het is ongedefinieerd.
In deze vergelijking, substitueer eensquote:
[..]
2ln(2x+y) moet gelijk aan nul zijn. Ik bedoelde eigenlijkHet linkerlid levert 1, het rechterlid 0.
Je weet uit je vergelijking dat 2ln(2x+y)=0. Als je dit zowel links als rechts invult krijg je aan beide kanten 0/0. Je mag dingen alleen wegdelen als je zeker weet dat ze niet gelijk aan 0 zijn.quote:
[..]
2ln(2x+y) moet gelijk aan nul zijn. Ik bedoelde eigenlijk
[..]
Waarom krijg je dan 0/0?
Ja, dan zie ik dat dit niet kan. Maar als wequote:
[..]
In deze vergelijking, substitueer eens. Snap je het dan?
Omdatquote:
[..]
Ja, dan zie ik dat dit niet kan. Maar als we
Want welke vergelijking waren we ook weer aan het oplossen?
Opinion is the medium between knowledge and ignorance (Plato)
Hoe zou je een vergelijking willen substitueren? Jij zegt nu in feite dat:quote:
[..]
Ja, dan zie ik dat dit niet kan. Maar als we
Wat natuurlijk nergens op slaat.
quote:
[..]
Omdat
Want welke vergelijking waren we ook weer aan het oplossen?
Ik denk dat ik 'm snap. Omdat 2ln(2x+y) gelijk aan nul is, kunnen we 2ln(2x+y) vervangen door 0 (ze zijn immers gelijk), en dat levert 0/0 = 0/0, en dat kan niet. Klopt deze beredenering?quote:
[..]
Hoe zou je een vergelijking willen substitueren? Jij zegt nu in feite dat:
Wat natuurlijk nergens op slaat.
Ik had de indruk dat hij het onderscheid nog niet kan maken tussen delen door nul en nul delen door.quote:
Om het even in een eenvoudiger voorbeeldje te vangen kijken we naar de vergelijking 2x - 6 = 0
Als we de denkfout van Rust zouden volgen, dan mogen we niet links en rechts delen door 2. Ik hoop maar dat ik wel links en rechts 6 mag optellen, en dan staat er 2x = 6. Mag ik nu wel door 2 delen links en rechts? Dan staat er namelijk x = 3, wat precies hetzelfde is als x - 3 = 0.
Waar het op neerkomt is dit: Ik weet dat twee maal "iets" gelijk is aan 0. Het kan dus niet anders, of "iets" moet zelf gelijk aan nul zijn.
Mijn advies is om daarom niet te onthouden wat er wel of niet zou mogen, maar te beredeneren of het mag. Uit het regeltje hierboven, of het triviale voorbeeld, zie je meteen dat het moet mogen. Dit gaat op voor veel meer rekenregels.
Ja.quote:
[..]
[..]
Ik denk dat ik 'm snap. Omdat 2ln(2x+y) gelijk aan nul is, kunnen we 2ln(2x+y) vervangen door 0 (ze zijn immers gelijk), en dat levert 0/0 = 0/0, en dat kan niet. Klopt deze beredenering?
Kunnen we dan ook niet zeggen dat 0 gelijk is aan 2ln(2x+y) (in deze vergelijking), en dat we krijgen 2ln(2x+y) = 2ln(2x+y) krijgen, wat we dan wel weer door 2ln(2x+y) kunnen delen? 't Blijft verwarrend voor me.quote:
Tja, het is niet eens zo zeer dat dat niet mag, maar je hebt er niets aan. Je houdt namelijk een triviale vergelijking over, (na aftrekken) 0=0. Een waarheid als een koe, maar je schiet er niets mee op.quote:
[..]
Kunnen we dan ook niet zeggen dat 0 gelijk is aan 2ln(2x+y) (in deze vergelijking), en dat we krijgen 2ln(2x+y) = 2ln(2x+y) krijgen, wat we dan wel weer door 2ln(2x+y) kunnen delen? 't Blijft verwarrend voor me.
Opinion is the medium between knowledge and ignorance (Plato)
Ah oké, duidelijk.quote:
[..]
Tja, het is niet eens zo zeer dat dat niet mag, maar je hebt er niets aan. Je houdt namelijk een triviale vergelijking over, (na aftrekken) 0=0. Een waarheid als een koe, maar je schiet er niets mee op.
Dit soort dingen vind ik het lastigst...
Ik heb je al vaker betrapt op kromme redeneringen, maar dit slaat alles.quote:
[..]
Ja, dan zie ik dat dit niet kan. Maar als we
Bekijk het eens zo. Als een product van twee (reële of complexe) grootheden gelijk is aan nul, dan kan dat alleen als (tenminste) één van die beide grootheden zelf gelijk is aan nul. Dus
AB = 0
is equivalent met
A = 0 ∨ B = 0
Als nu het product van 2 en ln(2x+y) gelijk is aan 0, dan zul je het met me eens moeten zijn dat ln(2x+y) gelijk is aan 0 aangezien tenminste één van de beide grootheden 2 en ln(x+2y) gelijk moet zijn aan nul en 2 evident niet gelijk is aan 0. In het algemeen volgt zo uit
AB = 0 ∧ A ≠ 0
dat
B = 0
hoewel je dit laatste niet om mag keren, aangezien het product van nul met zichzelf ook nul is. Je mag echter wel zeggen dat B = 0 equivalent is met AB = 0 onder de voorwaarde dat A ≠ 0.
Hebben we nu
AB = AC
dan is dit equivalent met
AB − AC = 0
en dit is weer equivalent met
A(B − C) = 0
en dit is weer equivalent met
A = 0 ∨ B − C = 0
en dit is weer equivalent met
A = 0 ∨ B = C
Dit betekent dat AB = AC equivalent is met B = C onder de voorwaarde dat A ≠ 0. Je mag dus beide leden van een vergelijking delen door eenzelfde grootheid om een equivalente vergelijking te bekomen onder de voorwaarde dat de grootheid waardoor je deelt ongelijk is aan nul. Dit geldt evenzeer als het rechterlid van de vergelijking gelijk is aan nul, want in AB = AC kan C best gelijk zijn aan nul. Anders gezegd, we kunnen het rechterlid van een vergelijking herleid op nul opvatten als het product van een grootheid ongelijk aan nul en nul, zodat we beide leden van die vergelijking door die grootheid ongelijk aan nul kunnen delen om een equivalente vergelijking te krijgen.
Klopt, als ik het zo opnieuw lees, slaat het nergens op. 2ln(2x+y) is namelijk niet gelijk aan 5.quote:
Ik heb je al vaker betrapt op kromme redeneringen, maar dit slaat alles.
Dank je voor je uitleg.
De uitleg is zeer duidelijk, en makkelijk te begrijpen. Ik waardeer het zeer dat je bereid bent om jouw tijd en moeite te steken in het schrijven van dit soort posts, met als doel om een ander iets te leren. Dat vind ik echt erg tof van je!
Hoe kun je weten dat de Lagrangian concaaf is en hoe weet je waarom het x = 9 of x = - 9 moet zijn..?!quote:
[..]
Dankje. Het zijn echt van die kleine dingen waar ik de fout in ga...
Zoals het volgende:
x² = 81 --> x = 9 of -9
Dat snap ik maar dan staat er:
Since the Lagrangian is concave, the solution is at x = 9 , y = 12 with lambda = 1/6
De formule is:
max f(x,y) = 3x + 4y subject to g(x,y) = x² + y² = 225
Omdat er een max staat is het concave volgens mij (?), maar hoezo is de oplossing alleen bij x = 9? Bij x = -9 rolt er toch ook gewoon y = 12 uit..?
-9² + y² = 225
y² = 225 - 81
y² = 144
y = 12.
[ Bericht 2% gewijzigd door Super-B op 18-10-2014 21:44:07 ]
Dus je zegt eerst A = 0, om dan vervolgens te zeggen: A = A. Wat is A/A dan?quote:
[..]
Kunnen we dan ook niet zeggen dat 0 gelijk is aan 2ln(2x+y) (in deze vergelijking), en dat we krijgen 2ln(2x+y) = 2ln(2x+y) krijgen, wat we dan wel weer door 2ln(2x+y) kunnen delen? 't Blijft verwarrend voor me.
A = 0quote:Op zaterdag 18 oktober 2014 22:14 schreef Amoeba het volgende:
[..]
Dus je zegt eerst A = 0, om dan vervolgens te zeggen: A = A. Wat is A/A dan?
A = A
A/A = 0/0 = niet gedefinieerd
Dus, is het zinnig om zoiets te zeggen?quote:
[..]
A = 0
A = A
A/A = 0/0 = niet gedefinieerd
Nee. Ik heb nooit geleerd wat een vergelijking eigenlijk letterlijk inhoudt, dit is de eerste keer dat ik me dit realiseer.quote:
[..]
Dus, is het zinnig om zoiets te zeggen?
Zou iemand mij kunnen helpen met iets kleins?
Ln | x - 2 | kun je splitsen in
ln ( x - 2) en ln ( 2 - x ). Echter vraag ik mij af wanneer de één geldt en wanneer de ander. Weet iemand dit?
Ln | x - 2 | kun je splitsen in
ln ( x - 2) en ln ( 2 - x ). Echter vraag ik mij af wanneer de één geldt en wanneer de ander. Weet iemand dit?
Weet je wat |x| betekent?quote:
Zou iemand mij kunnen helpen met iets kleins?
Ln | x - 2 | kun je splitsen in
ln ( x - 2) en ln ( 2 - x ). Echter vraag ik mij af wanneer de één geldt en wanneer de ander. Weet iemand dit?
Ik heb waarschijnlijk voor dit topic een relatief domme vraag, maar ik kan er zelf echt niet uitkomen aangezien ik al jaren geen wiskunde meer heb gehad.
A*44800000/(800000 + A) = 4000000
De uitkomst is 78431, maar ik heb geen flauw benul van hoe je hier op kan komen.
A*44800000/(800000 + A) = 4000000
De uitkomst is 78431, maar ik heb geen flauw benul van hoe je hier op kan komen.
Vergeef me dat ik even wat nullen weglaat (5)quote:
Ik heb waarschijnlijk voor dit topic een relatief domme vraag, maar ik kan er zelf echt niet uitkomen aangezien ik al jaren geen wiskunde meer heb gehad.
A*44800000/(800000 + A) = 4000000
De uitkomst is 78431, maar ik heb geen flauw benul van hoe je hier op kan komen.
A*448/(8 + A) = 40
448A = 40(8+A)
448A = 320 + 40A
408A = 320
A = 320/408 = 0,784314..
Opinion is the medium between knowledge and ignorance (Plato)
Dankjewel!quote:
[..]
Vergeef me dat ik even wat nullen weglaat (5)
A*448/(8 + A) = 40
448A = 40(8+A)
448A = 320 + 40A
408A = 320
A = 320/408 = 0,784314..
Misschien nu een hele domme vraag, maar waarom 'kan' die (8 + A) ineens naar de andere kant worden gehaald? Of heeft dat te maken met het opheffen van het delen door teken?
Vermenigvuldig de vergelijking links en rechts met (8 + A).quote:
[..]
Dankjewel!
Misschien nu een hele domme vraag, maar waarom 'kan' die (8 + A) ineens naar de andere kant worden gehaald? Of heeft dat te maken met het opheffen van het delen door teken?
Opinion is the medium between knowledge and ignorance (Plato)
Vrijdag is het wiskunde tentamen. Donderdag heb ik nog een tentamen voor een ander vak, dus ik ga mij daar morgen en overmogen voor voorbereiden.
Ik had vandaag twee tentamens van vorig jaar gemaakt en heb voor de eerste een 6.5 a 7.0 en voor de tweede daarna een 7.5 a 8.5.
Hopelijk komt het goed. Heb mij erg goed voorbereid en ik vind alles gelukkig makkelijk. Alleen nog een paar lastige opgaven uit het boek waar ik nog naar ga kijken. Tentamenvragen daarentegen zijn gelukkig makkelijk.
Ik wil bij deze iedereen bedanken voor de aangeboden hulp in de afgelopen weken!
Ik had vandaag twee tentamens van vorig jaar gemaakt en heb voor de eerste een 6.5 a 7.0 en voor de tweede daarna een 7.5 a 8.5.
Hopelijk komt het goed. Heb mij erg goed voorbereid en ik vind alles gelukkig makkelijk. Alleen nog een paar lastige opgaven uit het boek waar ik nog naar ga kijken. Tentamenvragen daarentegen zijn gelukkig makkelijk.
Ik wil bij deze iedereen bedanken voor de aangeboden hulp in de afgelopen weken!
Veel succes!quote:
Vrijdag is het wiskunde tentamen. Donderdag heb ik nog een tentamen voor een ander vak, dus ik ga mij daar morgen en overmogen voor voorbereiden.
Ik had vandaag twee tentamens van vorig jaar gemaakt en heb voor de eerste een 6.5 a 7.0 en voor de tweede daarna een 7.5 a 8.5.
Hopelijk komt het goed. Heb mij erg goed voorbereid en ik vind alles gelukkig makkelijk. Alleen nog een paar lastige opgaven uit het boek waar ik nog naar ga kijken. Tentamenvragen daarentegen zijn gelukkig makkelijk.
Ik wil bij deze iedereen bedanken voor de aangeboden hulp in de afgelopen weken!
Opinion is the medium between knowledge and ignorance (Plato)
Moet het niet x = (5ey) / (1 + ey) zijn ?
ey (5-x) = x
5ey - ey) x = x
5ey = x + xey
5ey = x ( 1 + ey)
x = 5ey / (1 + ey)
Goed gezien.quote:
[ afbeelding ]
Moet het niet x = (5ey) / (1 + ey) zijn ?
ey (5-x) = x
5ey - ey) x = x
5ey = x + xey
5ey = x ( 1 + ey)
x = 5ey / (1 + ey)
Opinion is the medium between knowledge and ignorance (Plato)
Ja, goed gezien. Check.quote:
[ afbeelding ]
Moet het niet x = (5ey) / (1 + ey) zijn ?
Ook hier heb je gelijk. Lekker antwoordenboekje heb je gekregen. Of is dit een opdracht 'zoek de fout'?quote:
[ afbeelding ]
[ afbeelding ]
Moet het niet gewoon y zijn i.p.v. y² ?
Opinion is the medium between knowledge and ignorance (Plato)
Ik zou zeggen:quote:
[..]
Nee, nu heb je het niet goed gezien.
Kijk nog eens goed naar het gebruik van de kettingregel bij het (naar x) differentiëren van ln (yx+1)
d f(x,y) / du
u = yx + 1
f(x,y) = ln ( u)
f'x(x,y) = 1/u * u'
1 / (yx + 1) * y
y / (yx + 1)
Zie edit. Ik keek zelf even verkeerd, maar je afleiding klopt.quote:
[..]
Ik zou zeggen:
d f(x,y) / du
u = yx + 1
f(x,y) = ln ( u)
f'x(x,y) = 1/u * u'
1 / (yx + 1) * y
y / (yx + 1)
Opinion is the medium between knowledge and ignorance (Plato)
