SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Laten we eens beginnen met je notatie. Voor de logaritme met een grondtal oftewel basis b van een getal a wordt in de Angelsaksische wereld, en dus ongetwijfeld ook in je Engelstalige boek,quote:
logb a
geschreven, en je ziet dat hier de basis b in subscript wordt genoteerd achter het generieke symbool log voor de logaritme. Ik ben altijd tegen deze notatie geweest, omdat vooral in handschrift het dan al heel gauw lijkt of er log ba staat, en dat is iets heel anders. En tegenwoordig heb je dan mensen zoals jij die niet weten hoe je een letter moet subscripten of daar gewoon te lui voor zijn, en dan krijg je dit soort ellende. Bovendien maak jij hier de ellende nog groter door het getal waarvan de logaritme moet worden genomen onterecht te superscripten, en dan is het hek van de dam.
In Nederland, maar ook in een aantal andere landen in Europa werd vroeger altijd gebruik gemaakt van de notatie
blog a
voor de logaritme met grondtal b van het getal a, en dit is een veel betere notatie, omdat de basis nu niet verward kan worden met het getal waarvan we de logaritme nemen. Uiteraard moet je dan niet vergeten de basis te superscripten, zodat deze niet verward kan worden met een factor voor het log symbool.
Ook de formule voor het omzetten van een logaritme naar een andere basis is met deze notatie veel gemakkelijker te onthouden en op te schrijven, vooral als we de zogeheten kettingvorm gebruiken. Stel dat we
blog a
willen uitdrukken in de logaritme van a met een ander grondtal g, dan schrijven we eerst de identiteit die we hiervoor gebruiken in de zogeheten kettingvorm
glog b · blog a = glog a
en dan zien we meteen dat
blog a = glog a / glog b
en in het bijzonder hebben we voor g = e dan
blog a = ln a / ln b
Als je bovenstaande identiteit in kettingvorm in de Angelsaksische notatie zou willen opschrijven, dan heb je
logg b · logb a = logg a
en dan zie je dat het hele kettingeffect weg is en dat je nu een formule hebt die je opeens niet meer gemakkelijk kunt memoriseren en opschrijven, en die dus ongetwijfeld fouten in de hand gaat werken. Kortom, niet gebruiken dus, die Angelsaksische notatie voor de basis van een logaritme.
Nu terug naar je vraag. Je wil kennelijk de vergelijking
xlog(e2) = 2
oplossen. Welnu, de logaritme met een (positief) grondtal x van e2 is per definitie de exponent waartoe we x moeten verheffen om e2 te verkrijgen, en deze exponent moet volgens de vergelijking 2 zijn. Dus hebben we
x2 = e2
en daarmee
x = e
En inderdaad is elog(e2) = ln(e2) = 2. Als je dit niet begrijpt dan begrijp je nog steeds niet wat een logaritme is.
[ Bericht 0% gewijzigd door Riparius op 21-09-2014 03:24:51 ]


Ik vroeg me af waarom Ø (de empty set) één partitie heeft. Ik zou intuitief zeggen dat deze geen partities heeft. Komt het doordat elk element in Ø 'nonempty' is? Er zijn immers geen elementen in Ø.
[ Bericht 2% gewijzigd door zerak op 19-09-2014 19:52:50 ]
[ Bericht 2% gewijzigd door zerak op 19-09-2014 19:52:50 ]


1.quote:Op vrijdag 19 september 2014 21:47 schreef RustCohle het volgende:
[ afbeelding ]
Van dit snap ik de overgang niet van een stap naar het ander.. hoe je dus opeens het volgende krijgt:
[ afbeelding ]
[ afbeelding ]
Tenslotte snap ik opgave b niet. Laatste zin vanaf ''omdat'' begrijp ik dus niet...
ey(x + 1) = x + 5
eyx - x = 5 - ey
x(ey - 1) = 5 - ey
ey(x + 1) = x + 5 ↔ x(ey - 1) = 5 - ey
2.
Weet je iets over inverse functies? Dan zou je moeten weten dat het bereik van de oorspronkelijke functie het domein van de inverse functie is.


Voor dit soort gevallen is het vaak handig om naar de definitie te kijken (subtiele verschillen kunnen voor dit soort randgevallen cruciaal zijn). Ik heb even de definitie van de Engelse wikipedia gepakt (het is natuurlijk mogelijk dat jij een andere definitie gebruikt, ik weet niet in hoeverre die gestandaardiseerd is):quote:Op vrijdag 19 september 2014 19:37 schreef zerak het volgende:
Ik vroeg me af waarom Ø (de empty set) één partitie heeft. Ik zou intuitief zeggen dat deze geen partities heeft. Komt het doordat elk element in Ø 'nonempty' is? Er zijn immers geen elementen in Ø.
P is a partition of X if and only if:
1. P does not contain the empty set.
2. The union of the sets in P is equal to X. (The sets in P are said to cover X.)
3. The intersection of any two distinct sets in P is empty. (We say the elements of P are pairwise disjoint.)
En inderdaad voldoet P = Ø, X = Ø aan deze eisen. (P bevat immers niet de lege verzameling: hij is zelf de lege verzameling en bevat dus niks).


Thanks. Deze definitie komt aardig overeen met wat ik hier heb staan. Subtiel inderdaadquote:Op vrijdag 19 september 2014 22:08 schreef defineaz het volgende:
[..]
Voor dit soort gevallen is het vaak handig om naar de definitie te kijken (subtiele verschillen kunnen voor dit soort randgevallen cruciaal zijn). Ik heb even de definitie van de Engelse wikipedia gepakt (het is natuurlijk mogelijk dat jij een andere definitie gebruikt, ik weet niet in hoeverre die gestandaardiseerd is):
P is a partition of X if and only if:
1. P does not contain the empty set.
2. The union of the sets in P is equal to X. (The sets in P are said to cover X.)
3. The intersection of any two distinct sets in P is empty. (We say the elements of P are pairwise disjoint.)
En inderdaad voldoet P = Ø, X = Ø aan deze eisen. (P bevat immers niet de lege verzameling: hij is zelf de lege verzameling en bevat dus niks).


Ik snap dat niet..quote:Op vrijdag 19 september 2014 22:07 schreef zerak het volgende:
[..]
1.
ey(x + 1) = x + 5
eyx - x = 5 - ey
x(ey - 1) = 5 - ey
ey(x + 1) = x + 5 ↔
x(ey - 1) = 5 - ey
2.
Weet je iets over inverse functies? Dan zou je moeten weten dat het bereik van de oorspronkelijke functie het domein van de inverse functie is.
2. Ja.. dat weet ik toch begrijp ik het niet met de elementen en al..


Dit wordt echt nooit wat als je zulke elementaire herleidingen niet met je ogen dicht kunt uitvoeren.quote:
Je hebt
ey(x + 1) = x + 5
Haakjes uitwerken in het linkerlid geeft
eyx + ey = x + 5
Nu willen we x oplossen uit deze betrekking, en om dat te doen moeten we eerst zorgen dat alle termen met x in het linkerlid komen te staan en alle termen zonder x in het rechterlid. We trekken nu eerst ey van beide leden af, dat geeft
eyx = x + 5 − ey
Vervolgens trekken we x van beide leden af, en dan krijgen we
eyx − x = 5 − ey
Nu kunnen we bij de termen in het linkerlid een factor x buiten haakjes halen en krijgen we
x(ey − 1) = 5 − ey
Tenslotte delen we beide leden door (ey − 1) en zie, dan krijgen we
x = (5 − ey) / (ey − 1)
Je hebt een functie f die strict monotoon dalend is en die het interval [0, ∞) als domein heeft. De uitdrukking (x+5)/(x+1) heeft de waarde 5 voor x = 0 en neemt af in waarde als we x groter laten worden. Maar ... deze uitdrukking neemt niet onbegrensd af als we x onbegrensd toe laten nemen, want we hebben immersquote:2. Ja.. dat weet ik toch begrijp ik het niet met de elementen en al..
(x+5)/(x+1) = 1 + 4/(x+1)
en de breuk 4/(x+1) nadert tot nul als we x onbeperkt toe laten nemen. De waarde van de breuk (x+5)/(x+1) nadert dus tot 1 maar wordt nooit 1 als we x onbeperkt toe laten nemen. Dus, als we voor x een waarde kiezen op het interval [0, ∞) zijnde het domein van f, dan ligt de waarde van (x+5)/(x+1) op het interval (1, 5]. En dus ligt de waarde van ln((x+5)/(x+1)) oftewel de functiewaarde f(x) op het interval (0, ln 5] en dit is dan het bereik van de functie f.
De functie f beeldt het interval [0, ∞) af op het interval (0, ln 5], en dus beeldt de inverse f−1 van deze functie omgekeerd het interval (0, ln 5] af op het interval [0, ∞). Het domein van de inverse functie f−1 is dus het interval (0, ln 5].
[ Bericht 0% gewijzigd door Riparius op 20-09-2014 01:05:15 ]


Ik weet niet hoe je tot die breuk komt. Hoe zie je dat? Hoe weet je dat x nadert naar 1 maar nooit 1 wordt?en hoezo is het ln5 bij het antwoord ipv 5?quote:Op zaterdag 20 september 2014 00:54 schreef Riparius het volgende:
[..]
Dit wordt echt nooit wat als je zulke elementaire herleidingen niet met je ogen dicht kunt uitvoeren.
Je hebt
ey(x + 1) = x + 5
Haakjes uitwerken in het linkerlid geeft
eyx + ey = x + 5
Nu willen we x oplossen uit deze betrekking, en om dat te doen moeten we eerst zorgen dat alle termen met x in het linkerlid komen te staan en alle termen zonder x in het rechterlid. We trekken nu eerst ey van beide leden af, dat geeft
eyx = x + 5 − ey
Vervolgens trekken we x van beide leden af, en dan krijgen we
eyx − x = 5 − ey
Nu kunnen we bij de termen in het linkerlid een factor x buiten haakjes halen en krijgen we
x(ey − 1) = 5 − ey
Tenslotte delen we beide leden door (ey − 1) en zie, dan krijgen we
x = (5 − ey) / (ey − 1)
[..]
Je hebt een functie f die strict monotoon dalend is en die het interval [0, ∞) als domein heeft. De uitdrukking (x+5)/(x+1) heeft de waarde 5 voor x = 0 en neemt af in waarde als we x groter laten worden. Maar ... deze uitdrukking neemt niet onbegrensd af als we x onbegrensd toe laten nemen, want we hebben immers
(x+5)/(x+1) = 1 + 4/(x+1)
en de breuk 4/(x+1) nadert tot nul als we x onbeperkt toe laten nemen. De waarde van de breuk (x+5)/(x+1) nadert dus tot 1 maar wordt nooit 1 als we x onbeperkt toe laten nemen. Dus, als we voor x een waarde kiezen op het interval [0, ∞) zijnde het domein van f, dan ligt de waarde van (x+5)/(x+1) op het interval (1, 5]. En dus ligt de waarde van ln((x+5)/(x+1)) oftewel de functiewaarde f(x) op het interval (0, ln 5] en dit is dan het bereik van de functie f.
De functie f beeldt het interval [0, ∞) af op het interval (0, ln 5], en dus beeldt de inverse f−1 van deze functie omgekeerd het interval (0, ln 5] af op het interval [0, ∞). Het domein van de inverse functie f−1 is dus het interval (0, ln 5].
Mijn antwoord was (-oneindig,oneindig)


Dat is wel erg elementair.quote:Op zaterdag 20 september 2014 09:06 schreef RustCohle het volgende:
[..]
Ik weet niet hoe je tot die breuk komt. Hoe zie je dat? Hoe weet je dat x nadert naar 1 maar nooit 1 wordt?en hoezo is het ln5 bij het antwoord ipv 5?
Mijn antwoord was (-oneindig,oneindig)
Staartdeling
x+1 / x+5 \ 1
-------------------
4
Dus er komt 1 uit de deling en de rest is 4/(x+1).
Of:
(x+5)/(x+1) = (x+1+4)/(x+1) = 1 + 4/(x+1)
Snap je wel dat 1/x naar 0 nadert als x naar oneindig gaat?


Ja dat begrijp ik. Hoe kun je zien dat ik de functie moest herschrijven naar 1 + 4/(x+1) ?quote:Op zaterdag 20 september 2014 13:24 schreef thenxero het volgende:
[..]
Dat is wel erg elementair.
Staartdeling
x+1 / x+5 \ 1
-------------------
4
Dus er komt 1 uit de deling en de rest is 4/(x+1).
Of:
(x+5)/(x+1) = (x+1+4)/(x+1) = 1 + 4/(x+1)
Snap je wel dat 1/x naar 0 nadert als x naar oneindig gaat?
Wat ik niet begrijp is wat ze bedoelen met E (1,5], althans hoe ze erop komen? En waarom ln 5 en niet 5?


1.quote:Op zaterdag 20 september 2014 16:56 schreef RustCohle het volgende:
[..]
Ja dat begrijp ik. Hoe kun je zien dat ik de functie moest herschrijven naar 1 + 4/(x+1) ?
Wat ik niet begrijp is wat ze bedoelen met E (1,5], althans hoe ze erop komen? En waarom ln 5 en niet 5? [ afbeelding ]
http://nl.wikipedia.org/wiki/Element_(wiskunde)
2. Men praat over de functie (x+5)/(x+1), niet over de oorspronkelijke. Daarom moet van deze getallen het natuurlijk logaritme geworden nomen en dus ln(1) = 0 en ln(5). Hoezo snap je de nul wel en ln(5) niet?
[ Bericht 1% gewijzigd door zerak op 20-09-2014 18:07:59 ]


Vul eerst eens een concrete positieve waarde in voor x, bijvoorbeeld x = 2. Dan heb jequote:Op zaterdag 20 september 2014 09:06 schreef RustCohle het volgende:
[..]
Ik weet niet hoe je tot die breuk komt. Hoe zie je dat?
Dit kon vroeger ieder kind van 10 je vertellen. En ja, 4/3 is nog te schrijven als 1 + 1/3 zodat je uiteindelijk hebt 7/3 = 2 + 1/3, maar dat hebben we nu niet nodig. In het algemeen heb je
Dit is niet zo. Ik heb gezegd dat (x+5)/(x+1) tot 1 nadert maar nooit 1 wordt als we x onbeperkt toe laten nemen. Dat is heel iets anders. We hebbenquote:Hoe weet je dat x nadert naar tot 1 maar nooit 1 wordt?
De breuk 4/(x+1) nadert tot 0 maar wordt nooit 0 als we x onbeperkt toe laten nemen. Dit is eenvoudig in te zien. Stel dat we een x > 0 willen vinden zodanig dat
waarin ε een willekeurig klein te kiezen positief getal is. Dan is dit het geval als
en dus
en dus
De waarde van de breuk 4/(x+1) kan dus willekeurig dicht tot nul naderen, als we x maar groot genoeg maken. Willen we bijvoorbeeld de waarde van de breuk kleiner dan 0,001 laten worden, dus ε = 0,001, dan vertelt bovenstaande ongelijkheid ons dat dit het geval is voor elke x > 3999. Maar het is ook duidelijk dat de waarde van de breuk 4/(x+1) nooit gelijk aan nul kan worden: een breuk heeft immers uitsluitend de waarde nul als de teller nul is terwijl de noemer niet nul is. En dat is bij 4/(x+1) onmogelijk, want de teller heeft hier de vaste waarde 4.
Je kunt ook nog op een andere manier inzien dat de breuk (x+5)/(x+1) nooit de waarde 1 aan kan nemen. Immers, stel dat
dan moet dus gelden
maar dit is onmogelijk, want dan zou 5 gelijk moeten zijn aan 1 en dat is niet zo.
We hebben gezien dat de waarde van de breukquote:en hoezo is het ln 5 bij het antwoord i.p.v. 5?
gelijk is aan 5 voor x = 0 en dat de waarde van deze breuk gestaag oftewel strict monotoon afneemt als we x steeds groter laten worden, en dat de waarde van de breuk daarbij willekeurig dicht nadert tot 1 maar nooit 1 wordt. Dat betekent dus dat de waarde van de breuk het interval (1, 5] doorloopt als we x het interval [0, ∞) laten doorlopen. Maar nu gaat het niet om de waarden van deze breuk, maar om de waarden die de functie met het functievoorschrift
aanneemt als we x het (gegeven) domein [0, ∞) laten doorlopen. Aangezien (x+5)/(x+1) de waarde 5 heeft voor x = 0 en willekeurig dicht nadert tot de waarde 1 als we x onbeperkt toe laten nemen en ln(1) = 0 volgt dus dat de functiewaarde f(x) het interval (ln 1, ln 5] oftewel (0, ln 5] doorloopt, en dit is dus het bereik van deze functie f.
De functie f geeft een afbeelding van het interval [0, ∞) op het interval (0, ln 5] en de inverse functie f−1 van deze functie f met als functievoorschrift
geeft dus een afbeelding van het interval (0, ln 5] op het interval [0, ∞). Het domein van f−1 is dus het interval (0, ln 5]. In onderstaand plaatje is de grafiek van f weergegeven in rood en de grafiek van f−1 in blauw. Tevens is de lijn met vergelijking y = x weergegeven in zwart. De grafieken van f en f−1 zijn elkaars spiegelbeeld bij spiegeling in deze lijn.
Zwei Dinge sind unendlich, das Universum und die menschliche Dummheit, aber bei dem Universum bin ich mir noch nicht ganz sicher.quote:Mijn antwoord was (-oneindig,oneindig)
--- Albert Einstein
[ Bericht 2% gewijzigd door Riparius op 21-09-2014 09:01:32 ]


"In deze opgave gaat het over getallen van vijf cijfers, waarin alleen de cijfers 2, 3, 4, 5, 6, 7 en 8 voorkomen."
"Hoeveel van die getallen zijn er in het geval dat: elk cijfer maar een keer gebruikt mag worden en het getal groter dan 54 000 moet zijn?"
Ik heb: 1*5*5*4*3 + 3*6*5*4*3. Ik ben niet zo goed in combinatoriek, dus daarom vraag ik me af of dit klopt.
"Hoeveel van die getallen zijn er in het geval dat: elk cijfer maar een keer gebruikt mag worden en het getal groter dan 54 000 moet zijn?"
Ik heb: 1*5*5*4*3 + 3*6*5*4*3. Ik ben niet zo goed in combinatoriek, dus daarom vraag ik me af of dit klopt.


Volgens mij niet helemaal.quote:Op zondag 21 september 2014 11:08 schreef netchip het volgende:
"In deze opgave gaat het over getallen van vijf cijfers, waarin alleen de cijfers 2, 3, 4, 5, 6, 7 en 8 voorkomen."
"Hoeveel van die getallen zijn er in het geval dat: elk cijfer maar een keer gebruikt mag worden en het getal groter dan 54 000 moet zijn?"
Ik heb: 1*5*5*4*3 + 3*6*5*4*3. Ik ben niet zo goed in combinatoriek, dus daarom vraag ik me af of dit klopt.
Voor alle getallen >60.000 heb je (inderdaad) 3 * 6*5*4*3 mogelijkheden, namelijk voor het eerste cijfer 3 mogelijkheden (6-7-8) en dan achtereenvolgens 6, 5, 4 en 3 opties.
Voor alle getallen tussen 54.000 en 59.999 heb je 1 * 4 * 5*4*3 opties, namelijk: cijfer 1 een 5, cijfer 2 is 4, 6, 7 of 8, en dan nog 5*4*3 willekeurige opties.
[ Bericht 0% gewijzigd door Janneke141 op 21-09-2014 14:49:35 ]
Opinion is the medium between knowledge and ignorance (Plato)


Dank je, ik zie het nu!quote:Op zondag 21 september 2014 14:21 schreef Janneke141 het volgende:
[..]
Volgens mij niet helemaal.
Voor alle getallen >60.000 heb je (inderdaad) 3 * 6*5*4*3 mogelijkheden, namelijk voor het eerste cijfer 3 mogelijkheden (6-7-8) en dan achtereenvolgens 6, 5, 4 en 3 opties.
Voor alle getallen tussen 54.000 en 59.999 heb je 1 * 4 * 5*4*3 opties, namelijk: cijfer 1 een 5, cijfer 2 is 4, 6, 7 of 8, en dan nog 5*4*3 willekeurige opties.


Hoe bereken je exact
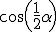
met
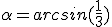
zonder gebruik te maken van halve hoek-identiteiten?
Het betreft opgave 17.46.e van Basisboek Wiskunde.
met
zonder gebruik te maken van halve hoek-identiteiten?
Het betreft opgave 17.46.e van Basisboek Wiskunde.


Meetkundig?quote:Op zondag 21 september 2014 15:27 schreef jungiaan het volgende:
Hoe bereken je exact
met
zonder gebruik te maken van halve hoek-identiteiten?
Het betreft opgave 17.46.e van Basisboek Wiskunde.
Opinion is the medium between knowledge and ignorance (Plato)


Bij de andere opgaven van 17.46 had ik gebruik gemaakt vanquote:
En in een rechthoekige driehoek is dus de overstaande zijde van hoek
Kan je hier iets mee?


Het zijn allebei vragen waarvoor je wat voorkennis nodig hebt. Je moet het bijbehorende hoofdstuk waarschijnlijk nog even doorlezen. Voor de eerste kan je gebruikmaken voor de formule voor cos(a + b), of voor cos(2a). De tweede is ook iets wat je eigenlijk gewoon uit je hoofd moet weten.quote:Op zondag 21 september 2014 15:27 schreef jungiaan het volgende:
Hoe bereken je exact
met
zonder gebruik te maken van halve hoek-identiteiten?
Het betreft opgave 17.46.e van Basisboek Wiskunde.
Voor de tweede, kijk eens naar de hoeken en lengtes van een gelijkzijdige driehoek met zijde 1 (en trek een middenloodlijn/bisectrice vanuit een zijde). Dit is een trucje om achter enkele veelgebruikte waarden van de sinus en cosinus te komen.
Ik neem aan dat er in je basisboek wiskunde ook wel een tabel met waarden van de sinus en de cosinus staat, maar ik vind het zelf een beter manier om die gelijkzijdige driehoek te tekenen, omdat je die procedure, in tegenstelling tot de specifieke waarden van de sinus en de cosinus voor die hoeken, niet zo snel vergeet.


Ik vraag me af waarom je deze opgave wil oplossen zonder gebruik van de identiteiten voor de halve hoek (c.q. de identiteiten voor de dubbele hoek). Van de Craats zegt namelijk expliciet (p. 140) dat je deze identiteiten moet gebruiken.quote:Op zondag 21 september 2014 15:52 schreef jungiaan het volgende:
[..]
Bij de andere opgaven van 17.46 had ik gebruik gemaakt van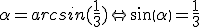
En in een rechthoekige driehoek is dus de overstaande zijde van hoekgelijk aan 1 en de hypotenusa gelijk aan 3. De andere zijde rekende ik dan uit met de stelling van Pythagoras.
Kan je hier iets mee?
Ik kom op
maar WolframAlpha weet geen exacte uitdrukking te produceren voor ½α, dus een meetkundige oplossing (afgezien van een meetkundig equivalent van het gebruik van de identiteiten voor de halve c.q. de dubbele hoek) lijkt me hier niet voor de hand te liggen.


Met de halve hoek-identiteiten(van Wikipedia) lukt het mij ook wel, maar aangezien deze nog niet waren afgeleid in de theorie gebruikte ik deze niet. Hoe zou ik de benodigde halve hoek-identiteit af moeten leiden uit bijv. de som/dubbele hoek formules zoals defineaz suggereert?


Je moet toch beter je boek lezen, want Van de Craats leidt de formules voor cos ½α en sin ½α af voordat jouw opgave aan bod komt.quote:Op zondag 21 september 2014 17:11 schreef jungiaan het volgende:
Met de halve hoek-identiteiten(van Wikipedia) lukt het mij ook wel, maar aangezien deze nog niet waren afgeleid in de theorie gebruikte ik deze niet. Hoe zou ik de benodigde halve hoek-identiteit af moeten leiden uit bijv. de som/dubbele hoek formules zoals defineaz suggereert?
Als het goed is heb je cos α al bepaald en daarvoor vind je dan
Nu kun je gebruik maken van de identiteit voor de cosinus van de dubbele hoek, waarbij je dan α vervangt door ½α zodat je krijgt
Je zult nog wel een geneste vierkantswortel moeten herleiden om het resultaat te verkrijgen dat ik hierboven geef, en ik betwijfel of je dat kunt, aangezien dat tegenwoordig niet meer wordt onderwezen.


Nee, de fout zit in het onderstreepte stukje.quote:Op zondag 21 september 2014 17:39 schreef rumiii het volgende:
Is het volgende correct?
f= x / ((x^2)+8)
f ' = ( (x^2) + 8 - 3x) / ( (x^2) + 8)^2
Opinion is the medium between knowledge and ignorance (Plato)




