Het grote bèta-studenten topic! #19 2 woorden, 9 letters

Index

» school, studie en onderwijs

actieve topics nieuwe topics
abonnement Unibet Coolblue Bitvavo
pi_140724633
quote:
0s.gif Op woensdag 4 juni 2014 21:18 schreef netchip het volgende:

[..]

Wiskunde B is verplicht voor mijn jaarlaag wanneer je natuurkunde gaat doen in de bovenbouw. :) Het blijkt dus dat veel mensen met Wiskunde A het niet aankunnen. Zelf snap ik niet dat je geen Wiskunde B gaat doen, als je natuurkunde doet, maar dat ben ik :P

* netchip is wiskunde fan en kiest Wiskunde B+D

Toevoeging: wel jammer, dat er niet uitgelegd wordt hoe het werkelijk zit. Kan in mijn klas ook niet, want klasgenoten hebben een driehoek nodig omdat ze niet begrijpen dat R = U/I een gevolg is uit U = I * R (of P = I2 * R, dat je dan de R kan vervangen door U/I waardoor je krijgt: P = U * I). Beetje jammer soms, want ik zou het wel graag willen leren.
Ik weet nu nog steeds niet waarover jij graag extra uitleg zou willen: de wet van Ohm, waarom je een vervangingsweerstand berekent zoals je dat doet of iets anders.

Voor de wet van Ohm kan je een waterval als analogie gebruiken. Hoe groter de hoogte van de waterval hoe groter de spanning. Hoe meer water er stroomt, dus hoe breder de waterval, hoe meer stroom. De analogie loopt mank op het punt van evenredigheid maar dat doet er nu niet toe. Als je bij eenzelfde spanning een X keer zo'n hoge weerstand hebt dan heb je X keer zo weinig stroom en omgekeerd. Waarom dit zo is? In eerste instantie werd het gewoon vastgesteld door proeven te doen, later hebben ze het verklaard. Dit is wellicht interessant om te lezen: http://en.wikipedia.org/wiki/Ohm%27s_law#Microscopic_origins

Detail: de weerstand verandert in lichte mate door de temperatuur op het moment dat er stroom doorheen iets loopt (vermogen wat wordt afgegeven aan die draad of weerstand), dit effect is dermate klein dat het niet relevant is voor jou.
Ander detail wat je helpt om je inzicht te vergroten: je moet je niet voorstellen dat elk electron een knikker is (dat is wel juist!) en dat de knikkers steeds met eenzelfde snelheid bewegen (dat is niet juist!), stel je voor dat de knikkers willekeurig in alle richtingen bewegen met verschillende snelheden ten gevolge van botsingen tegen andere knikkers (of de atomen van de draad of de weerstand) en dat dankzij de spanning statistisch gezien een groter aantal knikkers in de richting van de relatief positieve spanning beweegt.

Tenslotte nog maar even de opmerking dat stroom wordt voorgesteld als de verplaatsing van positieve deeltjes dus de omgekeerde richting van de verplaatsing van electronen maar dit wist je al als het goed is. Een historische blunder die nooit is hersteld. :N

[ Bericht 6% gewijzigd door Bram_van_Loon op 04-06-2014 22:18:02 ]
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
pi_140724988
quote:
0s.gif Op woensdag 4 juni 2014 22:07 schreef Bram_van_Loon het volgende:

[..]

Ik weet nu nog steeds niet waarover jij graag extra uitleg zou willen: de wet van Ohm, waarom je een vervangingsweerstand berekent zoals je dat doet of iets anders.
Waarop de wet van Ohm gebaseerd is, waarom die is zoals hij is. Definities die ik ken: stroom is bewegende lading, spanning is de oorzaak van stroom, weerstand is volt/ampere.

Waarschijnlijk zijn de definities van spanning en weerstand verkeerd, maar zo heb ik ze geleerd.
pi_140725207
quote:
1s.gif Op woensdag 4 juni 2014 22:12 schreef netchip het volgende:

[..]

Waarop de wet van Ohm gebaseerd is, waarom die is zoals hij is. Definities die ik ken: stroom is bewegende lading, spanning is de oorzaak van stroom, weerstand is volt/ampere.

Waarschijnlijk zijn de definities van spanning en weerstand verkeerd, maar zo heb ik ze geleerd.
Ik heb nog even wat toegevoegd aan die reactie.

Goed trouwens dat je Wiskunde D hebt gekozen.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
  woensdag 4 juni 2014 @ 22:44:55 #54
344036 MrStalin
lekker gewerkt pik
pi_140726846
quote:
0s.gif Op woensdag 4 juni 2014 22:02 schreef Bram_van_Loon het volgende:
Heeft iemand een idee waarom het zo belachelijke lang duurt om Matlab te installeren? Zo'n drie kwartier op een voor deze tijd modale desktop.
Heb je de studentenversie? Zo niet, dan heb je waarschijnlijk een variant met alle packages -> heel veel om te installeren.
pi_140727337
quote:
0s.gif Op woensdag 4 juni 2014 22:44 schreef MrStalin het volgende:

[..]

Heb je de studentenversie? Zo niet, dan heb je waarschijnlijk een variant met alle packages -> heel veel om te installeren.
Ik heb allerlei packages maar ik heb moeite om de grootte van het programma te rijmen met die extreem lange installatietijd.
8,6/9,4 gig groot (size/size on disk) met ruim driehonderdduizend bestanden. Misschien ligt het aan het grote aantal bestanden?
Zou het ook te maken hebben met allerlei rekenwerk i.v.m. compilatie en misschien ook wel extractie?
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
pi_140727466
Netchip, heb jij geleerd hoe je een derdegraadsvergelijking oplost?
Bijvoorbeeld x^3 - 3x^2 - 9x + 27 = 0
Je mag aannemen dat de oplossingen gehele getallen zijn.
Best handig om te kunnen en op de universiteit wordt het niet altijd uitgelegd terwijl je het soms wel moet kunnen.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
pi_140727703
quote:
0s.gif Op woensdag 4 juni 2014 22:57 schreef Bram_van_Loon het volgende:
Netchip, heb jij geleerd hoe je een derdegraadsvergelijking oplost?
Bijvoorbeeld x^3 - 3x^2 - 9x + 27 = 0
Je mag aannemen dat de oplossingen gehele getallen zijn.
Best handig om te kunnen en op de universiteit wordt het niet altijd uitgelegd terwijl je het soms wel moet kunnen.
Cardano is mij wel geleerd bij wiskunde D. En als je die eerste oplossing hebt dan een staartdeling doen. Ration Root Theorem is ons niet geleerd, maar het is bij jouw vraag vrij duidelijk dat
SPOILER
Om spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
een oplossing is.
pi_140727743
quote:
0s.gif Op woensdag 4 juni 2014 22:57 schreef Bram_van_Loon het volgende:
Netchip, heb jij geleerd hoe je een derdegraadsvergelijking oplost?
Bijvoorbeeld x^3 - 3x^2 - 9x + 27 = 0
Je mag aannemen dat de oplossingen gehele getallen zijn.
Best handig om te kunnen en op de universiteit wordt het niet altijd uitgelegd terwijl je het soms wel moet kunnen.
Ik heb geen idee... Tweedegraads vergelijkingen kan ik wel, evenals x7-25 = 0, bijvoorbeeld.

Ik heb iets geprobeerd met het ontbinden in factoren van jouw vergelijking, geen idee ofdat het klopt: x = 0 of/en (x-3)2 = 0 of/en -(x-3)2 = 0.

Toevoeging: ik had namelijk: x2(x-3)2-9(x-3) = 0 => -9x2(x-3)2 = 0.
pi_140727845
quote:
0s.gif Op woensdag 4 juni 2014 23:03 schreef netchip het volgende:

[..]

Ik heb geen idee... Tweedegraads vergelijkingen kan ik wel, evenals x7-25 = 0, bijvoorbeeld.

Ik heb iets geprobeerd met het ontbinden in factoren van jouw vergelijking, geen idee ofdat het klopt: x = 0 of/en (x-3)2 = 0 of/en -(x-3)2 = 0.
Tip: http://en.wikipedia.org/wiki/Rational_root_theorem + http://en.wikipedia.org/wiki/Polynomial_long_division
pi_140727924
Hoezo zou je moeilijk doen? Gewoon ontbinden in factoren, misschien ook wat beter te doen voor iemand uit 3 vwo.
Gist is liefde, gist is leven. Vooral in een vagijn.
pi_140728006
quote:
0s.gif Op woensdag 4 juni 2014 23:06 schreef Novermars het volgende:

[..]

Tip: http://en.wikipedia.org/wiki/Rational_root_theorem + http://en.wikipedia.org/wiki/Polynomial_long_division
Post geupdate met hoe ik het had aangepakt ^^

Klopt alleen niets van, zie ik nu. Ik had in dit geval namelijk maar 2 oplossingen gevonden: x = 0 of/en x = 3.
pi_140728165
quote:
14s.gif Op woensdag 4 juni 2014 23:07 schreef Rezania het volgende:
Hoezo zou je moeilijk doen? Gewoon ontbinden in factoren, misschien ook wat beter te doen voor iemand uit 3 vwo.
Staartdeling is basisschoolniveau en de RRT is ongeveer de makkelijkste stelling die je gaat tegenkomen.

Verder is het heel knap als jij in een keer kan zien in welke factoren je moet ontbinden, maar meestal gaat dit niet zo makkelijk.
pi_140728255
quote:
0s.gif Op woensdag 4 juni 2014 23:12 schreef Novermars het volgende:

[..]

Staartdeling is basisschoolniveau en de RRT is ongeveer de makkelijkste stelling die je gaat tegenkomen.

Verder is het heel knap als jij in een keer kan zien in welke factoren je moet ontbinden, maar meestal gaat dit niet zo makkelijk.
Staartdeling? Is afgeschaft toen ik op de basisschool leerde delen, haakdelingen, zijn het nu. Nooit een staartdeling geleerd :{
pi_140728276
quote:
0s.gif Op woensdag 4 juni 2014 23:12 schreef Novermars het volgende:

[..]

Staartdeling is basisschoolniveau en de RRT is ongeveer de makkelijkste stelling die je gaat tegenkomen.
Staartdeling wordt op de basisschool behandelt? Werd niet bij mij gedaan in ieder geval. :') Naar die theorie had ik nog niet gekeken, maar als het goed is moet netchip al kunnen ontbinden. Hij kan dit oplossen zonder nieuwe theorieën te leren. Maar misschien dat het voor andere derdegraadsvergelijkingen wel handig is om die theorie te leren.
quote:
Verder is het heel knap als jij in een keer kan zien in welke factoren je moet ontbinden, maar meestal gaat dit niet zo makkelijk.
Bij deze is het wel erg makkelijk. :P

[ Bericht 0% gewijzigd door Rezania op 04-06-2014 23:22:32 ]
Gist is liefde, gist is leven. Vooral in een vagijn.
pi_140729625
Een uitwerking:
Gevraagd: Los op: x^3 - 3x^2 - 9x + 27 = 0
Volgens de RRT zijn de rationale oplossingen in de vorm van x_1 = \pm \dfrac{1,3,9,27}{1} = \{1,-1,3,-3,9,-9,27,-27\}. Als we dit lijstje af gaan zien we dan de eerste oplossing x=3 is. Nu we een oplossing hebben gaan wij onze veelterm proberen te schrijven als y = (x-3)(ax^2 + bx +c). Dit kan (voor zover ik weet) op twee manieren, waarvan ik nu de moeilijkste kies ^^
Normaal gesproken bij ik behoorlijk pro-LaTeX, maar ik heb geen zin om op te zoeken hoe ik een staartdeling typeset, dus ik doe het maar ouderwets met pen en papier:

Oftewel, de oplossingen zijn x \in \{3,-3\}

Bonus: Gebruik de RRT om te bewijzen dat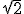 \sqrt{2} irrationaal is.

[ Bericht 3% gewijzigd door Novermars op 05-06-2014 19:53:51 ]
  donderdag 5 juni 2014 @ 00:46:07 #66
122648 Bravebart
København er på plads ja
pi_140731853
quote:
14s.gif Op woensdag 4 juni 2014 22:05 schreef Rezania het volgende:
Tevens, morgen pas college vanaf het vijfde uur. _O_ Wel tot het achtste uur helaas. -O- Maar ja, lekker uitslapen dus. *O*

Ook zo stom. Die docent waar ik morgen college van krijg is lid van de KNAW. Ouderejaars en de opleidingsdirecteur en zo zijn helemaal laaiend over hem, zeggen dat het een groot privilege is dat we college krijgen van hem. Maar hij is gewoon slecht qua college geven, gewoon echt slecht. :')_! Al die mensen die verblind zijn door zijn lidmaatschap. :') Ach, sowieso een slecht vak helaas.
Whehe, ja college kunnen geven is een vak apart :P Voorbeelden te over van geniale wetenschappers met belabberde colleges :P

Wie krijg je btw?
Op donderdag 22 november 2012 00:14 schreef ondeugend het volgende:
liefdevolle gevoelens voor de duisternis
pi_140732518
quote:
10s.gif Op donderdag 5 juni 2014 00:46 schreef Bravebart het volgende:

[..]

Whehe, ja college kunnen geven is een vak apart :P Voorbeelden te over van geniale wetenschappers met belabberde colleges :P

Wie krijg je btw?
Sef Heijnen. Stond ook een interview met hem in de laatste Vision of Life (maar ik weet niet of je die nog ontvangt).
Gist is liefde, gist is leven. Vooral in een vagijn.
pi_140732659
Ik moet voor het aanvragen van het bachelordiploma alle gehaalde vakken + cijfers invullen op een formulier.
Dat staat toch allemaal op Usis, wtf?!
  donderdag 5 juni 2014 @ 01:38:08 #69
122648 Bravebart
København er på plads ja
pi_140732961
quote:
1s.gif Op donderdag 5 juni 2014 01:12 schreef Rezania het volgende:

[..]

Sef Heijnen. Stond ook een interview met hem in de laatste Vision of Life (maar ik weet niet of je die nog ontvangt).
Baas _O_ College geven met overheadsheets _O_

Verder wel eens, je bent tegenwoordig zo gewend aan ppt's dat dit wel ff lastig is :P
Op donderdag 22 november 2012 00:14 schreef ondeugend het volgende:
liefdevolle gevoelens voor de duisternis
pi_140734295
quote:
10s.gif Op donderdag 5 juni 2014 01:20 schreef Anoonumos het volgende:
Ik moet voor het aanvragen van het bachelordiploma alle gehaalde vakken + cijfers invullen op een formulier.
Dat staat toch allemaal op Usis, wtf?!
Nice, dus alsnog cum laude geslaagd?
pi_140734710
quote:
0s.gif Op woensdag 4 juni 2014 23:44 schreef Novermars het volgende:
Een uitwerking:
Gevraagd: Los op: x^3 - 3x^2 - 9x + 27 = 0
Volgens de RRT zijn de rationele oplossingen in de vorm van x_1 = \pm \dfrac{1,3,9,27}{1} = \{1,-1,3,-3,9,-9,27,-27\}. Als we dit lijstje af gaan zien we dan de eerste oplossing x=3 is. Nu we een oplossing hebben gaan wij onze veelterm proberen te schrijven als y = (x-3)(ax^2 + bx +c). Dit kan (voor zover ik weet) op twee manieren, waarvan ik nu de moeilijkste kies ^^
Normaal gesproken bij ik behoorlijk pro-LaTeX, maar ik heb geen zin om op te zoeken hoe ik een staartdeling typeset, dus ik doe het maar ouderwets met pen en papier:
[ afbeelding ]
Oftewel, de oplossingen zijn x \in \{3,-3\}

Bonus: Gebruik de RRT om te bewijzen dat \sqrt{2} irrationeel is.
(ir)rationaal
pi_140739292
quote:
10s.gif Op donderdag 5 juni 2014 01:20 schreef Anoonumos het volgende:
Ik moet voor het aanvragen van het bachelordiploma alle gehaalde vakken + cijfers invullen op een formulier.
Dat staat toch allemaal op Usis, wtf?!
Bacheloraanvraag moet expliciet via de examencommissie gaan, een verzoek wat je zelf in moet dienen dus het is niet een kwestie 'ja maar je kunt toch zien dat dit zo in mijn digitale cijferlijst staat'?
pi_140756248
quote:
4s.gif Op donderdag 5 juni 2014 07:45 schreef thabit het volgende:

[..]

(ir)rationaal
Oops, fixed!
pi_140764384
Yes, 4 dagen weekend. :9
Gist is liefde, gist is leven. Vooral in een vagijn.
pi_140764391
En nog maar 1 college dit jaar. *G*
Gist is liefde, gist is leven. Vooral in een vagijn.
pi_140765782
:(
pi_140765858
quote:
0s.gif Op donderdag 5 juni 2014 23:32 schreef Fierce. het volgende:
:(
Nou, iemand is jaloers blijkbaar.
Gist is liefde, gist is leven. Vooral in een vagijn.
pi_140765908
Klopt!
pi_140766930
quote:
0s.gif Op donderdag 5 juni 2014 23:35 schreef Fierce. het volgende:
Klopt!
Ik heb nog wel een paar practica, een toets en een tentamen hoor. Het is niet allemaal zo geweldig als het klinkt.
Gist is liefde, gist is leven. Vooral in een vagijn.
pi_140767198
Ha gay
pi_140767209
quote:
14s.gif Op vrijdag 6 juni 2014 00:09 schreef Amoeba het volgende:
Ha gay
Je keek in de spiegel?
Gist is liefde, gist is leven. Vooral in een vagijn.
pi_140767288
quote:
7s.gif Op vrijdag 6 juni 2014 00:10 schreef Rezania het volgende:

[..]

Je keek in de spiegel?
:Y
pi_140767483
quote:
7s.gif Op vrijdag 6 juni 2014 00:12 schreef Amoeba het volgende:

[..]

:Y
Er staat een klein (wiskundig) vraagje op de vorige pagina, ben benieuwd of je deze kan oplossen!
pi_140767550
quote:
0s.gif Op vrijdag 6 juni 2014 00:19 schreef Novermars het volgende:

[..]

Er staat een klein (wiskundig) vraagje op de vorige pagina, ben benieuwd of je deze kan oplossen!
Het is bijna half 1 man. _O-
Zal er morgen naar kijken.
  vrijdag 6 juni 2014 @ 01:21:07 #85
302898 RockNijntje
Je dagelijkse dosis Zillennial
pi_140768797
quote:
10s.gif Op maandag 2 juni 2014 21:23 schreef Rezania het volgende:

[..]

Dat doe ik liever met jou, volgens Nijn ben je raakbaar. :9
Doerak.
Als je mij ziet posten ben ik verdwaald in het verleden of mis ik jullie
  vrijdag 6 juni 2014 @ 02:25:19 #86
337465 Bram_van_Loon
Jeff, we can!
pi_140769583
quote:
0s.gif Op vrijdag 6 juni 2014 00:19 schreef Novermars het volgende:

[..]

Er staat een klein (wiskundig) vraagje op de vorige pagina, ben benieuwd of je deze kan oplossen!
Er staan ook nog 3 vragen van Riparius open. Hij hoopt blijkbaar nog steeds dat er ooit een wiskundig genie langskomt die de juiste trucjes vindt waarmee die integralen een dusdanige vorm krijgen dat ze wel op te lossen zijn met standaard regeltjes en technieken. Gaan we ooit nog de oplossing krijgen of vinden? ;(
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
pi_140769633
quote:
0s.gif Op vrijdag 6 juni 2014 02:25 schreef Bram_van_Loon het volgende:

[..]

Er staan ook nog 3 vragen van Riparius open. Hij hoopt blijkbaar nog steeds dat er ooit een wiskundig genie langskomt die de juiste trucjes vindt waarmee die integralen een dusdanige vorm krijgen dat ze wel op te lossen zijn met standaard regeltjes en technieken. Gaan we ooit nog de oplossing krijgen of vinden? ;(
Ik dacht zelf aan de Residustelling, maar mijn complexe analyse is te ver weggezakt om het te proberen. En hem kennende moet het kunnen met meer elementaire wiskunde.
  vrijdag 6 juni 2014 @ 02:32:52 #88
337465 Bram_van_Loon
Jeff, we can!
pi_140769639
quote:
0s.gif Op vrijdag 6 juni 2014 02:32 schreef Anoonumos het volgende:En hem kennende moet het kunnen met meer elementaire wiskunde.
Daar kan je vergif op innemen. ;)
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
pi_140770249
quote:
0s.gif Op vrijdag 6 juni 2014 00:19 schreef Novermars het volgende:

[..]

Er staat een klein (wiskundig) vraagje op de vorige pagina, ben benieuwd of je deze kan oplossen!
Je bedoelt het bewijs dat √2 irrationaal is mbh van de rational root theorem?

quote:
0s.gif Op vrijdag 6 juni 2014 02:25 schreef Bram_van_Loon het volgende:

[..]

Er staan ook nog 3 vragen van Riparius open. Hij hoopt blijkbaar nog steeds dat er ooit een wiskundig genie langskomt die de juiste trucjes vindt waarmee die integralen een dusdanige vorm krijgen dat ze wel op te lossen zijn met standaard regeltjes en technieken. Gaan we ooit nog de oplossing krijgen of vinden? ;(
Heb je een linkje?
Niet dat ik ze kan oplossen, want dat heb ik al eerder geprobeerd, maar ik wil ze nog wel een keer bekijken.:P
pi_140770735
quote:
0s.gif Op woensdag 4 juni 2014 22:57 schreef Bram_van_Loon het volgende:
Netchip, heb jij geleerd hoe je een derdegraadsvergelijking oplost?
Bijvoorbeeld x^3 - 3x^2 - 9x + 27 = 0
Je mag aannemen dat de oplossingen gehele getallen zijn.
Best handig om te kunnen en op de universiteit wordt het niet altijd uitgelegd terwijl je het soms wel moet kunnen.
Engineering solution:

Gooi het in Matlab of Mathematica. In ieder geval Matlab heeft hier gewoon een commando voor, dus met 1 regel ben je klaar. :P
pi_140770781
quote:
0s.gif Op vrijdag 6 juni 2014 07:59 schreef Lilliesleaf het volgende:

[..]

Engineering solution:

Gooi het in Matlab of Mathematica. In ieder geval Matlab heeft hier gewoon een commando voor, dus met 1 regel ben je klaar. :P
Foei.
pi_140773728
quote:
0s.gif Op vrijdag 6 juni 2014 05:15 schreef defineaz het volgende:

[..]

Heb je een linkje?
Niet dat ik ze kan oplossen, want dat heb ik al eerder geprobeerd, maar ik wil ze nog wel een keer bekijken.:P
SES / Wiskunde B en Economische studies.
pi_140779337
quote:
0s.gif Op vrijdag 6 juni 2014 02:25 schreef Bram_van_Loon het volgende:

[..]

Er staan ook nog 3 vragen van Riparius open. Hij hoopt blijkbaar nog steeds dat er ooit een wiskundig genie langskomt die de juiste trucjes vindt waarmee die integralen een dusdanige vorm krijgen dat ze wel op te lossen zijn met standaard regeltjes en technieken. Gaan we ooit nog de oplossing krijgen of vinden? ;(
Ze zijn mij alle 3 gelukt, maar niet met elementaire technieken helaas. Met name bij de eerste integraal is mijn oplossing behoorlijk complex; ik zal kijken of ik daar wat simpelers kan verzinnen.

De derde is met Taylorreeksen wel te doen. Dan komt er vrij snel
-\left(\frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \cdots\right) = -\frac{\pi^2}{6}
uit.

De tweede begint met een substitutie x=exp(t), om de noemer wat te vereenvoudigen:
\int_0^1\frac{x-1}{\log x}dx = \int_{-\infty}^0(e^{2t}-e^t)\frac{dt}{t}.
Ik vervang hier graag t door -t, en zo krijgen we:
\int_0^\infty(e^{-t}-e^{-2t})\frac{dt}{t}.
Nu komt de truc: introduceer een variabele s, en definieer
f(s) = \int_0^\infty(e^{-t}-e^{-2t})t^{s-1}dt.
De opdracht is dus om f(0) te bepalen.

Waarom de extra variabele s introduceren? Omdat we daarin de Gamma-functie herkennen:
\Gamma(s)=\int_0^\infty e^{-t}t^{s-1}dt.
Deze Gamma-functie is een analytische uitbreiding van de faculteit:
\Gamma(n) = (n-1)!

Een leuke eigenschap van de Gamma-functie is:
\Gamma(s)\alpha^{-s} = \int_0^\infty e^{-\alpha t} t^{s-1}dt.
Kijk hoe wonderbaarlijk dit is: links is \alpha een grondtal, en rechts is het een exponent! Deze identiteit kun je behoorlijk vaak toepassen om deze reden.

We zien in elk geval:
f(s) = \Gamma(s)(1-2^{-s}).
De relatie met de faculteit helpt ons op dit punt helaas niet verder, want (-1)! is niet gedefinieerd. Wel is het zo dat als s in de buurt van 0 zit, dat dan geldt:
\Gamma(s) = 1/s + O(1).
Ook geldt
2^{-s} = e^{-(\log 2) s} = 1 - (\log 2)s + O(s^2).
Uiteindelijk zien we dus voor s in de buurt van 0:
f(s) = \Gamma(s)(1-2^{-s}) = \left(1/s + O(1)\right)\left((\log 2)s + O(s^2)\right) = \log 2 + O(s).
Dus de integraal is f(0) = log 2. Zal vast eenvoudiger kunnen, maar ik vond dit wel illustratief.
pi_140780404
quote:
0s.gif Op woensdag 4 juni 2014 22:57 schreef Bram_van_Loon het volgende:
Netchip, heb jij geleerd hoe je een derdegraadsvergelijking oplost?
Bijvoorbeeld x^3 - 3x^2 - 9x + 27 = 0
Je mag aannemen dat de oplossingen gehele getallen zijn.
Best handig om te kunnen en op de universiteit wordt het niet altijd uitgelegd terwijl je het soms wel moet kunnen.
Dit is een beetje een dead giveaway, de coëfficiënten zijn afgezien van het teken machten van 3, en daarmee zie je direct dat x = 3 voldoet. En dan is de eerste afgeleide 3x2 − 6x − 9 ook nog eens nul voor x = 3, zodat we dus een nulpunt x = 3 met multipliciteit 2 hebben, aangezien het polynoom duidelijk niet (x −3)3 is. En de derde wortel moet dan x = −3 zijn aangezien de som van de wortels 3 moet zijn.
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
pi_140785636
Beetje jammer dat ik vandaag niet naar de TU ben geweest.
quote:
Today Adrian van Hooydonk, Director of BMW Group Design, dropped by his old faculty. He gave a guest lecture about his newest design: the BMW i8
SPOILER
Om spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
:~ Stond voor IO zo te zien.

[ Bericht 2% gewijzigd door Rezania op 06-06-2014 18:38:03 ]
Gist is liefde, gist is leven. Vooral in een vagijn.
pi_140786058
quote:
0s.gif Op vrijdag 6 juni 2014 05:15 schreef defineaz het volgende:

[..]

Je bedoelt het bewijs dat √2 irrationaal is mbh van de rational root theorem?
Jup!
  vrijdag 6 juni 2014 @ 18:56:48 #97
337465 Bram_van_Loon
Jeff, we can!
pi_140786358
quote:
0s.gif Op vrijdag 6 juni 2014 18:20 schreef Rezania het volgende:
Beetje jammer dat ik vandaag niet naar de TU ben geweest.

[..]

:~ Stond voor IO zo te zien.
Het ziet er aardig uit. Dit blijft mijn favoriet maar dan in een andere kleur:
Alleen is het jammer dat ze niet voor normale deuren hebben gekozen.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
pi_140786385
quote:
0s.gif Op vrijdag 6 juni 2014 18:56 schreef Bram_van_Loon het volgende:

[..]

Het ziet er aardig uit. Dit blijft mijn favoriet maar dan in een andere kleur: [ afbeelding ]
Alleen is het jammer dat ze niet voor normale deuren hebben gekozen.
Moet je die deur nou indrukken om hem te openen? _O-
Gist is liefde, gist is leven. Vooral in een vagijn.
  vrijdag 6 juni 2014 @ 18:58:39 #99
337465 Bram_van_Loon
Jeff, we can!
pi_140786399
quote:
0s.gif Op vrijdag 6 juni 2014 18:57 schreef Rezania het volgende:

[..]

Moet je die deur nou indrukken om hem te openen? _O-
De deuren openen schuin omhoog. :?
Het is niet echt praktisch.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
  vrijdag 6 juni 2014 @ 19:06:25 #100
337465 Bram_van_Loon
Jeff, we can!
pi_140786588
Nu het toch over auto's gaat, hebben jullie de Bugatti Veyron in actie gezien? Een auto waarvan een deel van vorm verandert zo gauw je met een sleutel de stand van een schakelaar wijzigt.
Bugatti Super Sport Speed Test - Top Gear - BBC
Bugatti Super Sport Speed Test - Top Gear - BBC
Niet alleen is dat technisch gezien leuk, het is ook nodig om de auto road legal te maken, in de 'sportstand' krijg je die auto al snel niet op de snelweg of het circuit. De specs zijn verbluffend, wat er allemaal nodig is om +430 km/u te rijden, hoeveel brandstof dat kost en hoe snel de banden versleten geraken. Ter illustratie, als je op een fiets 40 km/u fietst dan moet je al ongeveer 2 keer zoveel vermogen leveren als wanneer je 30 km/u fietst dankzij de ongeveer kwadratisch toenemende luchtweerstand in functie van de snelheid (ook de rolweerstand neemt toe maar slechts lineair).
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
actieve topics nieuwe topics
abonnement Unibet Coolblue Bitvavo
Het grote bèta-studenten topic! #19 2 woorden, 9 letters
Index

» school, studie en onderwijs

Forum Opties
Forumhop:
Hop naar:
(afkorting, bv 'KLB')