SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Dat laatste is spot-on, maar niet de reden waarom je een fout maakt.quote:Op woensdag 9 juli 2014 21:33 schreef netchip het volgende:
[..]
Ben nog bezig met het volledig uitdenken, dit is wat ik tot nu toe heb:. Bij mijn voorbeeld 55i is x is 5.
. Die 5log kan je dan omrekenen door te doen: ln(5)/ln(5).
Ik heb het gevoel dat ik iets mis. Het meest logische zou zijn dat de rekenregels voor complexe getallen niet hetzelfde zijn als voor de reele getallen.
We weten dat
Met dit alles, probeer het eens opnieuw!
[ Bericht 3% gewijzigd door Novermars op 10-07-2014 19:08:21 ]
Was ik achtergekomen.quote:
[..]
de log is een natuurlijk logarithme niet 5log.
5 log 5 is dus 5 * log 5
Echter, als je als grondtal voor het logaritme 5 neemt, dan is 5log(5) = 1. Dat rekende wat makkelijker. Maar het blijkt fout te zijn. Dus nog maar even verder denken.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 21% gewijzigd door thabit op 09-07-2014 22:01:48 ]
De principle branch is de enige branch die ertoe doet!quote:
[..]
Verder ben je natuurlijk nog (i arg 5) vergeten.
Dus er komen oneindig veel antwoorden uit.
@Thabit, laat hem zelf even nadenken...
quote:
[..]
Dat laatste is spot-on, maar niet de reden waarom je een fout maakt.
We weten dat, waar
en dat
en dat in de Engelstalige literatuur dat [tex \ln (x) = \log (x)[/tex]
Met dit alles, probeer het eens opnieuw!
Wel jammer dat thabit de oplossing al heeft gepost. Toch ga ik verder zoeken naar nog een manier. Zou je misschien nog een interessante vraag willen posten?
Laat eens je stappen zien, want je doet volgens mij hele vreemde dingen...quote:
[..], tja, en nu?
Wel jammer dat thabit de oplossing al heeft gepost. Toch ga ik verder zoeken naar nog een manier. Zou je misschien nog een interessante vraag willen posten?
En ik wil dat best doen, maar probeer dit eerst maar degelijk te begrijpen.
quote:
[..]
Laat eens je stappen zien, want je doet volgens mij hele vreemde dingen...
En ik wil dat best doen, maar probeer dit eerst maar degelijk te begrijpen.
Ah, daar had ik niet eens aan gedacht. In my defense, je hebt er niks aan om het zo te doen.quote:
[..]. Dan neem ik het natuurlijk logaritme van beide kanten. Als je dan de haakjes wegwerkt kom je op dat uit...
Schrijf
Voordat je kunt begrijpen waaromquote:
Hoe zit het met 'complexe' exponenten? Als je de identiteit van Euler hebt,, hoe kan je e dan verheffen tot de macht i maal pi?
eiπ = −1
moet je wel het een en ander weten over complexe getallen en trouwens ook over analyse. Een complex getal z kun je opvatten als een lineaire combinatie van de reële eenheid 1 en de imaginaire eenheid i, dus
z = x·1 + y·i
waarbij x en y scalaire (reële) grootheden zijn. Aangezien x·1 = x schrijft men dit meestal als z = x + yi of als z = x + iy. Omdat een complex getal volledig is bepaald door de coëfficiënten x en y van de reële resp. de imaginaire eenheid en daarmee door het geordende paar reële getallen (x, y) kun je een complex getal z = x + iy op een eenduidige manier weergeven als het punt met coördinaten (x, y) in een vlak voorzien van een cartesisch assenstelsel. We spreken dan ook wel van het complexe vlak.
Als y = 0 dan is z = x·1 + 0·i = x een reëel getal, zodat de x-as dus de 'gewone' reële getallenlijn representeert in het complexe vlak. De x-as heet dan ook de reële as als we werken met een assenstelsel als grafische voorstelling van de complexe getallen. Als x = 0 dan is z = 0·1 + y·i = yi een getal dat men ook wel een 'zuiver imaginair' getal noemt, omdat het complexe getal dan geen reële component heeft. Deze getallen worden uiteraard afgebeeld op de y-as, die daarom de imaginaire as wordt genoemd wanneer we werken met een assenstelsel om complexe getallen grafisch voor te stellen.
Het punt (1, 0) is het beeldpunt van de reële eenheid 1 (omdat 1 = 1·1 + 0·i) en het punt (0, 1) is het beeldpunt van de imaginaire eenheid i (omdat i = 0·1 + 1·i). Als we 1 vermenigvuldigen met i dan krijgen we 1·i = i, zodat we ook kunnen zeggen dat het beeldpunt (1, 0) van het getal 1 door een vermenigvuldiging met i overgaat in het beeldpunt (0, 1) van het getal i. Vermenigvuldigen we i nu weer met i, dan krijgen we i·i = −1 met als beeldpunt het punt (−1, 0) zodat we kunnen zeggen dat het beeldpunt (0, 1) van i door een vermenigvuldiging met i overgaat in het beeldpunt (−1, 0) van het getal −1.
Kennelijk is het dus zo dat vermenigvuldiging met i, zowel van de reële eenheid 1 als van de imaginaire eenheid i, in het complexe vlak overeenkomt met een rotatie om de oorsprong over een rechte hoek tegen de klok in. Dit zie je uitgebeeld in het volgende plaatje:
Omdat vermenigvuldiging met i van zowel de reële eenheid 1 als de imaginaire eenheid i beantwoordt aan een rotatie om de oorsprong over een rechte hoek tegen de klok in, geldt ditzelfde ook voor elke lineaire combinatie z = x·1 + y·i en daarmee dus voor elk complex getal z. Het beeldpunt van het product z·i van een vermenigvuldiging van een willekeurig complex getal z met i ligt dus een kwartslag tegen de klok in om de oorsprong gedraaid ten opzichte van het beeldpunt van z. Nog een plaatje om dit te illustreren:
In dit plaatje is z = 2 + i met als beeldpunt (2, 1). Vermenigvuldiging met i geeft zi = (2 + i)i = 2i + i2 = 2i − 1 = −1 + 2i met als beeldpunt (−1, 2) en je ziet dat dit punt inderdaad een kwartslag tegen de klok in om de oorsprong gedraaid ligt ten opzichte van het beeldpunt (2, 1) van z = 2 + i. En uiteraard kunnen we zi weer met i vermenigvuldigen, en dan krijgen we zi2 = z·(−1) = −z = −2 − i met als beeldpunt (−2, −1). Na vier maal achtereen vermenigvuldigen met i hebben we vier maal een kwartslag tegen de klok in gemaakt zodat we dan weer terug zijn op ons uitgangspunt, en inderdaad is zi4 = z·1 = z.
Het is uiteraard niet toevallig dat vermenigvuldiging met i beantwoordt aan een rotatie om de oorsprong over een rechte hoek tegen de klok in, dat is een eenvoudige consequentie van de rekenregel i2 = −1 en de identificatie van het complexe getal z = x + yi met het punt (x, y) in een vlak voorzien van een cartesisch assenstelsel. Twee getallen die elkaars tegengestelde zijn hebben beeldpunten die diametraal liggen ten opzichte van de oorsprong, zodat je kunt zeggen dat vermenigvuldiging met −1 beantwoordt aan een rotatie over een halve slag rond de oorsprong. En omdat vermenigvuldigen met −1 hetzelfde is als tweemaal achtereen vermenigvuldigen met i beantwoordt eenmaal vermenigvuldigen met i dus aan een rotatie over de helft van een halve slag oftewel een kwartslag rond de oorsprong.
Nu kun je nog opmerken dat het bij een rotatie over een halve slag rond de oorsprong voor het resultaat niet uit maakt of we tegen de klok in of met de klok mee roteren, terwijl dit bij een rotatie over een kwart slag uiteraard wel verschil maakt. Ga zelf na dat vermenigvuldiging met −i beantwoordt aan een rotatie rond de oorsprong over een kwartslag met de klok mee. Twee kwartslagen met de klok mee leveren hetzelfde resultaat op als twee kwartslagen tegen de klok in, en inderdaad heb je (−i)·(−i) = −1 evenals i·i = −1.
Probeer nu eens of je mijn uitleg hier en hier over de formule van Euler enigszins kunt begrijpen.
[ Bericht 0% gewijzigd door Riparius op 09-07-2014 23:17:15 ]
Waarom doet alleen de principal branch ertoe?quote:
[..]
De principle branch is de enige branch die ertoe doet!
@Thabit, laat hem zelf even nadenken...
Lijkt mij dat dat anderen er ook toe doen.
x^2 = 1
doet natuurlijk niet alleen x = 1 ertoe.
Jouw uitleg snap ik opzich wel, maar ik heb geen idee wat een parametervoorstelling is... Verder weet ik vaag wat de eenheidscirkel is, de definitie van de sinus en cosinus in de eenheidscirkel ken ik echter niet.quote:
[..]
Voordat je kunt begrijpen waarom
eiπ = −1
moet je wel het een en ander weten over complexe getallen en trouwens ook over analyse. Een complex getal z kun je opvatten als een lineaire combinatie van de reële eenheid 1 en de imaginaire eenheid i, dus
z = x·1 + y·i
waarbij x en y scalaire (reële) grootheden zijn. Aangezien x·1 = x schrijft men dit meestal als z = x + yi of als z = x + iy. Omdat een complex getal volledig is bepaald door de coëfficiënten x en y van de reële resp. de imaginaire eenheid en daarmee door het geordende paar reële getallen (x, y) kun je een complex getal z = x + iy op een eenduidige manier weergeven als het punt met coördinaten (x, y) in een vlak voorzien van een cartesisch assenstelsel. We spreken dan ook wel van het complexe vlak.
Als y = 0 dan is z = x·1 + 0·i = x een reëel getal, zodat de x-as dus de 'gewone' reële getallenlijn representeert in het complexe vlak. De x-as heet dan ook de reële as als we werken met een assenstelsel als grafische voorstelling van de complexe getallen. Als x = 0 dan is z = 0·1 + y·i = yi een getal dat men ook wel een 'zuiver imaginair' getal noemt, omdat het complexe getal dan geen reële component heeft. Deze getallen worden uiteraard afgebeeld op de y-as, die daarom de imaginaire as wordt genoemd wanneer we werken met een assenstelsel om complexe getallen grafisch voor te stellen.
Het punt (1, 0) is het beeldpunt van de reële eenheid 1 (omdat 1 = 1·1 + 0·i) en het punt (0, 1) is het beeldpunt van de imaginaire eenheid i (omdat i = 0·1 + 1·i). Als we 1 vermenigvuldigen met i dan krijgen we 1·i = i, zodat we ook kunnen zeggen dat het beeldpunt (1, 0) van het getal 1 door een vermenigvuldiging met i overgaat in het beeldpunt (0, 1) van het getal i. Vermenigvuldigen we i nu weer met i, dan krijgen we i·i = −1 met als beeldpunt het punt (−1, 0) zodat we kunnen zeggen dat het beeldpunt (0, 1) van i door een vermenigvuldiging met i overgaat in het beeldpunt (−1, 0) van het getal −1.
Kennelijk is het dus zo dat vermenigvuldiging met i, zowel van de reële eenheid 1 als van de imaginaire eenheid i, in het complexe vlak overeenkomt met een rotatie om de oorsprong over een rechte hoek tegen de klok in. Dit zie je uitgebeeld in het volgende plaatje:
[ afbeelding ]
Omdat vermenigvuldiging met i van zowel de reële eenheid 1 als de imaginaire eenheid i beantwoordt aan een rotatie om de oorsprong over een rechte hoek tegen de klok in, geldt ditzelfde ook voor elke lineaire combinatie z = x·1 + y·i en daarmee dus voor elk complex getal z. Het beeldpunt van het product z·i van een vermenigvuldiging van een willekeurig complex getal z met i ligt dus een kwartslag tegen de klok in om de oorsprong gedraaid ten opzichte van het beeldpunt van z. Nog een plaatje om dit te illustreren:
[ afbeelding ]
In dit plaatje is z = 2 + i met als beeldpunt (2, 1). Vermenigvuldiging met i geeft zi = (2 + i)i = 2i + i2 = 2i − 1 = −1 + 2i met als beeldpunt (−1, 2) en je ziet dat dit punt inderdaad een kwartslag tegen de klok in om de oorsprong gedraaid ligt ten opzichte van het beeldpunt (2, 1) van z = 2 + i. En uiteraard kunnen we zi weer met i vermenigvuldigen, en dan krijgen we zi2 = z·(−1) = −z = −2 − i met als beeldpunt (−2, −1). Na vier maal achtereen vermenigvuldigen met i hebben we vier maal een kwartslag tegen de klok in gemaakt zodat we dan weer terug zijn op ons uitgangspunt, en inderdaad is zi4 = z·1 = z.
Het is uiteraard niet toevallig dat vermenigvuldiging met i beantwoordt aan een rotatie om de oorsprong over een rechte hoek tegen de klok in, dat is een eenvoudige consequentie van de rekenregel i2 = −1 en de identificatie van het complexe getal z = x + yi met het punt (x, y) in een vlak voorzien van een cartesisch assenstelsel. Twee getallen die elkaars tegengestelde zijn hebben beeldpunten die diametraal liggen ten opzichte van de oorsprong, zodat je kunt zeggen dat vermenigvuldiging met −1 beantwoordt aan een rotatie over een halve slag rond de oorsprong. En omdat vermenigvuldigen met −1 hetzelfde is als tweemaal achtereen vermenigvuldigen met i beantwoordt eenmaal vermenigvuldigen met i dus aan een rotatie over de helft van een halve slag oftewel een kwartslag rond de oorsprong.
Nu kun je nog opmerken dat het bij een rotatie over een halve slag rond de oorsprong voor het resultaat niet uit maakt of we tegen de klok in of met de klok mee roteren, terwijl dit bij een rotatie over een kwart slag uiteraard wel verschil maakt. Ga zelf na dat vermenigvuldiging met −i beantwoordt aan een rotatie rond de oorsprong over een kwartslag met de klok mee. Twee kwartslagen met de klok mee leveren hetzelfde resultaat op als twee kwartslagen tegen de klok in, en inderdaad heb je (−i)·(−i) = −1 evenals i·i = −1.
Probeer nu eens of je mijn uitleg hier en hier over de formule van Euler enigszins kunt begrijpen.
Dit zijn perfect dingen die je zelf kan googelen.quote:
[..]
Jouw uitleg snap ik opzich wel, maar ik heb geen idee wat een parametervoorstelling is... Verder weet ik vaag wat de eenheidscirkel is, de definitie van de sinus en cosinus in de eenheidscirkel ken ik echter niet.
Was maar een grapje om mijn falen te maskeren!quote:Op donderdag 10 juli 2014 14:08 schreef t4rt4rus het volgende:
[..]
Waarom doet alleen de principal branch ertoe?
Lijkt mij dat dat anderen er ook toe doen.
x^2 = 1
doet natuurlijk niet alleen x = 1 ertoe.
Heb ik gedaan. Concrete definities vinden is moeilijk.quote:
[..]
Dit zijn perfect dingen die je zelf kan googelen.
Ook al in het Engels geprobeerd?quote:
[..]
Heb ik gedaan. Concrete definities vinden is moeilijk.
Had ik nog niet gedaan. Nu wel, wat is de Nederlandse Wikipedia toch goedkoop bij de Engelse versie.quote:
Als Nederlanders Engels kunnen, waarom dan een aparte wiki?quote:
[..]
Had ik nog niet gedaan. Nu wel, wat is de Nederlandse Wikipedia toch goedkoop bij de Engelse versie.
We zijn toch geen Duitsers die alles inspreken in Duits.
Hetzelfde met studieboeken, waarom zou iemand die in het Nederlands gaan schrijven als je een veel groter Engelstalig publiek hebt.
Je weet dat je in een plat vlak voorzien van een cartesisch coördinatenstelsel rechte lijnen en curves kunt representeren door vergelijkingen in de variabelen x en y. Als je bijvoorbeeld gaat kijken naar de verzameling van alle punten waarvan de coördinaten (x, y) voldoen aan 2x + 3y = 7 dan vind je dat al deze punten op een rechte lijn liggen die door de punten (2, 1) en (5, −1) gaat. Daarom heet een vergelijking als deze ook een lineaire vergelijking in x en y (linea betekent 'lijn'). Maar je hebt uiteraard ook allerlei andere vergelijkingen in x en y. Als je bijvoorbeeld de vergelijking x² − y + 1 = 0 neemt en je gaat dan kijken naar alle punten waarvan de coördinaten (x, y) voldoen aan deze betrekking, dan vind je dat al deze punten een parabool vormen met een verticale symmetrie-as en met als top het punt (0, 1).quote:
[..]
Jouw uitleg snap ik opzich wel, maar ik heb geen idee wat een parametervoorstelling is... Verder weet ik vaag wat de eenheidscirkel is, de definitie van de sinus en cosinus in de eenheidscirkel ken ik echter niet.
Nu zie je dat we hier steeds één vergelijking hebben in de variabelen x en y, maar het is ook vaak handig om twee afzonderlijke vergelijkingen te hebben, namelijk eentje waarmee we de x-coördinaat van een punt op de curve of lijn direct uit kunnen rekenen en een tweede vergelijking waarmee we de bijbehorende y-coördinaat van hetzelfde punt op de curve of lijn direct uit kunnen rekenen. Maar dan hebben we wel een derde variabele nodig waar we x en y in uit kunnen drukken. Zo'n hulpvariabele noemen we een parameter en het samenstel van de twee vergelijkingen die ons vertellen hoe x en y elk afhangen van deze parameter noemen we dan een parametervoorstelling van de curve of lijn.
Het is gangbaar om voor de parameter de letter t te gebruiken, onder meer omdat in de fysica de letter t vaak wordt gebruikt om tijd aan te geven. Zo kun je dan de baan die een bewegend punt in een plat vlak aflegt beschrijven doordat je voor elk tijdstip t de coördinaten (x, y) van het punt op dat moment kunt bepalen aan de hand van een parametervoorstelling.
Een parametervoorstelling van de rechte lijn met vergelijking 2x + 3y = 7 is bijvoorbeeld
x = −3t + 2
y = 2t + 1
Als we hier t = 0 invullen, dan krijgen we x = 2 en y = 1, zodat we het punt (2, 1) op de lijn vinden. En als we hier t = −1 invullen dan krijgen we x = 5 en y = −1 zodat we het punt (5, −1) op de lijn vinden.
Een parametervoorstelling van een lijn of curve is nooit uniek, want we kunnen oneindig veel andere parametervoorstellingen bedenken die toch exact dezelfde curve of lijn opleveren. Je zou dezelfde lijn bijvoorbeeld ook weer kunnen geven door de parametervoorstelling
x = 3t + 5
y = −2t − 1
Nu zie je dat de waarde t = 0 van de parameter het punt (5, −1) geeft terwijl de waarde t = −1 het punt (2, 1) oplevert.
Uit een parametervoorstelling van een lijn of curve kun je vaak weer een vergelijking in x en y van de betreffende kromme of lijn verkrijgen. Dat lukt wanneer je erin slaagt om de parameter t uit het stelsel te elimineren. Bij een lineair stelsel zoals in dit voorbeeld is dit heel eenvoudig. Laten we uitgaan van de tweede parametervoorstelling. Als we beide leden van de eerste vergelijking voor x vermenigvuldigen met 2 en we vermenigvuldigen beide leden van de tweede vergelijking voor y met 3, dan krijgen we
2x = 6t + 10
3y = −6t − 3
Tellen we de leden van deze beide vergelijkingen nu bij elkaar op, dan krijgen we
2x + 3y = 6t + 10 − 6t − 3
en dus
2x + 3y = 7
en dat is inderdaad de vergelijking in x en y waar we mee begonnen.
Voor de parabool met als vergelijking x² − y + 1 = 0 zou je eenvoudig x = t kunnen nemen, en als je dit invult in de vergelijking krijg je t² − y + 1 = 0 en dus y = t2 + 1. Een parametervoorstelling van deze parabool is dus
x = t
y = t² + 1
Oefening: bedenk zelf nog een paar andere parametervoorstellingen voor deze zelfde parabool.
Dan de goniometrie. Een goed begrip van de definities van de sinus- en de cosinusfunctie aan de hand van de eenheidscirkel is absoluut onmisbaar als je je met complexe getallen bezig wil gaan houden. Je hebt al gezien dat een vermenigvuldiging met i in het complexe vlak beantwoordt aan een rotatie om de oorsprong over een rechte hoek in tegenwijzerzin. Welnu, het blijkt dat elke vermenigvuldiging met een complex getal ongelijk nul in het complexe vlak beantwoordt aan een draaistrekking, dat is een samenstelling van een rotatie rond de oorsprong en een meetkundige vermenigvuldiging (schaling) ten opzichte van de oorsprong. Daarom is het fundamenteel dat je begrijpt hoe je een complex getal
z = x + iy
omzet in de zogeheten goniometrische of polaire vorm
z = r(cos φ + i·sin φ)
Bestudeer nu eerst deze uitleg van mij over de definitie van de sinus- en de cosinusfunctie aan de hand van de eenheidscirkel.
[ Bericht 0% gewijzigd door Riparius op 12-07-2014 22:24:28 ]
Keer dit argument eens om. Waarom denk je dat Duitsers en bijvoorbeeld ook Fransen een eigen Wikipedia hebben als die volgens jou ook genoegen zouden kunnen nemen met de Engelse Wikipedia? Dat is echt geen kwestie van het niet beheersen van de Engelse taal. Aan universiteiten in Duitsland of Frankrijk hoef je niet aan te komen met leerboeken of dictaten in het Engels, ook niet voor wat meer gevorderde onderwerpen, dat zouden zowel de studenten als de hoogleraren niet pikken, en terecht.quote:
[..]
Als Nederlanders Engels kunnen, waarom dan een aparte wiki?
We zijn toch geen Duitsers die alles inspreken in Duits.
Het kleine Nederlandse taalgebied is inderdaad een probleem, vooral voor uitgevers die onvoldoende afzetmogelijkheden zien. Maar dat is vanuit het oogpunt van goed onderwijs een oneigenlijk argument en daarmee nog geen rechtvaardiging om de handdoek dan maar in de ring te werpen en te buigen voor Amerikaans (niet Engels) cultuurimperialisme.quote:Hetzelfde met studieboeken, waarom zou iemand die in het Nederlands gaan schrijven als je een veel groter Engelstalig publiek hebt?
Om te beginnen beheersen veel studenten (en hoogleraren!) het Engels veel minder goed dan ze zelf menen, en dat heeft een nefaste invloed op de kennisoverdracht alsmede op de kwaliteit van het geproduceerde lesmateriaal, voor zover er niet van bestaand Engelstalig (doorgaans Amerikaans) materiaal gebruik wordt gemaakt.
Daarnaast dreigt door de obsessie met het Engels een voornamelijk Amerikaanse monocultuur te ontstaan, en dat is ook voor een vak als wiskunde een slechte zaak. Ik zie heel vaak artikelen van Amerikaanse wiskundigen waarin (met name op historisch vlak) onjuiste beweringen worden gedaan of waaruit blijkt dat de auteur belangrijke literatuur over zijn of haar onderwerp niet kent. Dat komt doordat de meeste Amerikaanse wiskundigen kennelijk al lang niet meer in staat zijn vakliteratuur in het Duits en Frans te lezen, laat staan dat ze nog in staat zouden zijn een artikel van bijvoorbeeld Euler of Gauss in het Latijn te lezen (en nee, bij lange na niet alle geschriften uit het gigantische œuvre van Euler zijn vertaald).
Zo'n oefening:quote:
[..]
Je weet dat je in een plat vlak voorzien van een cartesisch coördinatenstelsel rechte lijnen en curves kunt representeren door vergelijkingen in de variabelen x en y. Als je bijvoorbeeld gaat kijken naar de verzameling van alle punten waarvan de coördinaten (x, y) voldoen aan 2x + 3y = 7 dan vind je dat al deze punten op een rechte lijn liggen die door de punten (2, 1) en (5, −1) gaat. Daarom heet een vergelijking als deze ook een lineaire vergelijking in x en y (linea betetekent 'lijn'). Maar je hebt uiteraard ook allerlei andere vergelijkingen in x en y. Als je bijvoorbeeld de vergelijking x² − y + 1 = 0 neemt en je gaat dan kijken naar alle punten waarvan de coördinaten (x, y) voldoen aan deze betrekking, dan vind je dat al deze punten een parabool vormen met een verticale symmetrie-as en met als top het punt (0, 1).
Nu zie je dat we hier steeds één vergelijking hebben in de variabelen x en y, maar het is ook vaak handig om twee afzonderlijke vergelijkingen te hebben, namelijk eentje waarmee we de x-coördinaat van een punt op de curve of lijn direct uit kunnen rekenen en een tweede vergelijking waarmee we de bijbehorende y-coördinaat van hetzelfde punt op de curve of lijn direct uit kunnen rekenen. Maar dan hebben we wel een derde variabele nodig waar we x en y in uit kunnen drukken. Zo'n hulpvariabele noemen we een parameter en het samenstel van de twee vergelijkingen die ons vertellen hoe x en y elk afhangen van deze parameter noemen we dan een parametervoorstelling van de curve of lijn.
Het is gebruikelijk om voor de parameter de letter t te gebruiken, onder meer omdat in de fysica de letter t vaak wordt gebruikt om tijd aan te geven. Zo kun je dan de baan die een bewegend punt in een plat vlak aflegt beschrijven doordat je voor elk tijdstip t de coördinaten (x, y) van het punt op dat moment kunt bepalen aan de hand van een parametervoorstelling.
Een parametervoorstelling van de rechte lijn met vergelijking 2x + 3y = 7 is bijvoorbeeld
x = −3t + 2
y = 2t + 1
Als we hier t = 0 invullen, dan krijgen we x = 2 en y = 1, zodat we het punt (2, 1) op de lijn vinden. En als we hier t = −1 invullen dan krijgen we x = 5 en y = −1 zodat we het punt (5, −1) op de lijn vinden.
Een parametervoorstelling van een lijn of curve is nooit uniek, want we kunnen oneindig veel andere parametervoorstellingen bedenken die toch exact dezelfde curve of lijn opleveren. Je zou dezelfde lijn bijvoorbeeld ook weer kunnen geven door de parametervoorstelling
x = 3t + 5
y = −2t −1
Nu zie je dat de waarde t = 0 van de parameter het punt (5, −1) geeft terwijl de waarde t = −1 het punt (2, 1) oplevert.
Uit een parametervoorstelling van een lijn of curve kun je vaak weer een vergelijking in x en y van de betreffende kromme of lijn verkrijgen. Dat lukt wanneer je er in slaagt om de parameter t uit het stelsel te elimineren. Bij een lineair stelsel zoals in dit voorbeeld is dit heel eenvoudig. Laten we uitgaan van de tweede parametervoorstelling. Als we beide leden van de eerste vergelijking voor x vermenigvuldigen met 2 en we vermenigvuldigen beide leden van de tweede vergelijking voor y met 3, dan krijgen we
2x = 6t + 10
3y = −6t −3
Tellen we de leden van deze beide vergelijkingen nu bij elkaar op, dan krijgen we
2x + 3y = 6t + 10 − 6t − 3
en dus
2x + 3y = 7
en dat is inderdaad de vergelijking in x en y waar we mee begonnen.
Voor de parabool met als vergelijking x² − y + 1 = 0 zou je eenvoudig x = t kunnen nemen, en als je dit invult in de vergelijking krijg je t² − y + 1 = 0 en dus y = t2 + 1. Een parametervoorstelling van deze parabool is dus
x = t
y = t² + 1
Oefening: bedenk zelf nog een paar andere parametervoorstellingen voor deze zelfde parabool.
Dan de goniometrie. Een goed begrip van de definities van de sinus- en cosinusfunctie aan de hand van de eenheidscirkel is absoluut onmisbaar als je je met complexe getallen bezig wil gaan houden. Je hebt al gezien dat een vermenigvuldiging met i in het complexe vlak beantwoordt aan een rotatie om de oorsprong over een rechte hoek in tegenwijzerzin. Welnu, het blijkt dat elke vermenigvuldiging met een complex getal ongelijk nul in het complexe vlak beantwoordt aan een draaistrekking, dat is een samenstelling van een rotatie rond de oorsprong en een meetkundige vermenigvuldiging (schaling) ten opzichte van de oorsprong. Daarom is het fundamenteel dat je begrijpt hoe je een complex getal
z = x + iy
omzet in de zogeheten goniometrische vorm
z = r(cos φ + i·sin φ)
Bestudeer nu eerst deze uitleg van mij over de definitie van de sinus- en de cosinusfuncties aan de hand van de eenheidscirkel.
Ik heb gedaan x2-y = -1. Daaruit heb ik opgesteld: x2 = 4t2-4 en -y = -4t2+3. Een parameterstelling is f(t) = x+y dus,
[ Bericht 0% gewijzigd door netchip op 10-07-2014 20:48:02 ]
Dit is niet dezelfde curve, want een vierkantswortel is niet negatief, zodat x hier geen negatieve waarden aan kan nemen. Je krijgt hiermee dan ook slechts een 'halve' parabool, kijk maar.quote:
[..]
Zo'n oefening:
Ik heb gedaan x2-y = -1. Daaruit heb ik opgesteld: x2 = 4t2-4 en -y = -4t2+3. Een parameterstelling is f(t) = x+y dus,en
. Is dit een van het oneindig aantal functies?
Stel dat ik dan zou definieren: f(t) = x2 - y. Met x2 = 4t2-4 en y = 4t2 - 3, zou het dan kloppen? (WolframAlpha geeft geen grafiek hierbij)quote:
[..]
Dit is niet dezelfde curve, want een vierkantswortel is niet negatief, zodat x hier geen negatieve waarden aan kan nemen. Je krijgt hiermee dan ook slechts een 'halve' parabool, kijk maar.
Je maakt het veel te moeilijk voor je zelf. Je wilt de PV van 
. Stel nu 
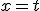en dan rolt er automatisch 
uit. Wat dus je PV is.
Riparius had die al gegeven.quote:
Je maakt het veel te moeilijk voor je zelf. Je wilt de PV van
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |