SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Dat is correct.quote:
Nog even een toelichting voor anderen die hier meelezen: we zochten twee grootheden waarvan het product −900q2 moest zijn en de som −11q. Het is duidelijk dat elk van de gezochte grootheden dan één factor q moet hebben, aangezien de som anders geen veelvoud van q kan zijn.
Verder moeten we dan zoeken naar twee getallen met als product −900 en als som −11. Het is duidelijk dat één van deze beide getallen negatief moet zijn en het andere positief. Als we de juiste tekens (plus of min) even buiten beschouwing laten betekent dit dat we zoeken naar twee getallen met als product 900 en waarvan het verschil 11 bedraagt. Louter uitproberen is bij wat grotere getallen niet zo handig, dan is het beter het product eerst te ontbinden in priemfactoren. Dit geeft
900 = 22·32·52
Nu is het duidelijk dat de gezochte getallen niet beide even kunnen zijn, omdat het verschil van twee even getallen weer even is, en dus niet 11 kan zijn. De beide factoren 2 moeten dus in één van de beide getallen zitten. Ook is het duidelijk dat het verschil van twee drievouden of twee vijfvouden weer een drievoud resp. een vijfvoud is, en dus niet 11 kan zijn. De beide factoren 3 moeten dus in één van de beide getallen zitten en de beide factoren 5 ook. Dan blijven er nog maar een paar mogelijkheden over en zie je snel dat 22·32 = 36 en 52 = 25 de gezochte getallen zijn, afgezien van de juiste tekens. Nu moeten we nog één van deze twee getallen van een minteken voorzien, en aangezien de som −11 moet zijn is het duidelijk dat 25 en −36 de gezochte getallen zijn.
De gezochte grootheden met als product −900q2 en als som −11q zijn dus 25q en −36q. We krijgen zo
30p2 − 11pq − 30q2 = 30p2 + 25pq − 36pq − 30q2 = 5p(6p + 5q) − 6q(6p + 5q) = (5p − 6q)(6p + 5q)
quote:Waarom leer ik zulke dingen niet op school? Ik kan me hier echt aan irriteren, ik zal opsommen wat ik de afgelopen drie jaar heb geleerd:
- Termen met gemeenschappelijke factoren optellen (zeg ik dit goed?)
- De hoeken in een driehoek zijn bij elkaar 180 graden
- Overstaande hoeken zijn hetzelfde
- Ontbinden van tweedegraads polynomen, met a = 1
- De abc-formule
- De goniometrische formules
That's it. Het is werkelijk schandalig.
[ Bericht 2% gewijzigd door Riparius op 29-06-2014 13:40:28 ]


Wow, dat deduceren van de kenmerken van de gezochte getallen is echt baas  ! Meestal voer ik dat onbewust uit (m.u.v. het ontbinden in priemfactoren en het bepalen dat één van de twee getallen even moet zijn), maar om het uitgeschreven te zien is toch wat anders.
! Meestal voer ik dat onbewust uit (m.u.v. het ontbinden in priemfactoren en het bepalen dat één van de twee getallen even moet zijn), maar om het uitgeschreven te zien is toch wat anders.


Lijkt me ook simpel genoeg om gewoon twee vergelijkingen dan op te stellen toch?
x*y = -900
x-y = -11
En dan rollen ze er ook zo uit. Hoewel dit priemfactoren verhaal ook wel nice is.
x*y = -900
x-y = -11
En dan rollen ze er ook zo uit. Hoewel dit priemfactoren verhaal ook wel nice is.


Als je dit stelsel wil oplossen (waarbij de som van de gezochte getallen −11 is, niet het verschil) en je elimineert één van de beide onbekenden, dan kom je weer uit op een vierkantsvergelijking. Dan draai je in een kringetje als je twee getallen zoekt waarvan product en som zijn gegeven teneinde een vierkantsvergelijking op te lossen door ontbinden in factoren. Stel namelijk dat je de vierkantsvergelijkingquote:Op zondag 29 juni 2014 00:54 schreef Inaithnir het volgende:
Lijkt me ook simpel genoeg om gewoon twee vergelijkingen dan op te stellen toch?
x*y = -900
x+y = -11
En dan rollen ze er ook zo uit. Hoewel dit priemfactoren verhaal ook wel nice is.
z2 − 11z − 900 = 0
zou willen oplossen door ontbinden in factoren. Dan moet je dus twee getallen x en y vinden waarvan de som −11 is en het product −900. Elimineer je echter de y uit bovenstaand stelsel, dan kom je uit op
x2 + 11x − 900 = 0
Wil je nu deze vergelijking oplossen door ontbinden in factoren, dan moet je twee getallen w en z vinden zodanig dat wz = −900 en w + z = 11. Elimineer je w uit dit stelsel, dan kom je weer uit op bovenstaande vergelijking in z, en daarmee ben je weer terug bij af.
Nu zul je waarschijnlijk tegenwerpen dat er ook andere methoden zijn om bovenstaande vierkantsvergelijking in x op te lossen, en dat klopt, maar daarmee schiet je wel je doel voorbij, want dan had je beter direct bovenstaande oorspronkelijke vergelijking in z op een andere manier kunnen oplossen dan door ontbinden in factoren.
Er is overigens wel een manier om deze vicieuze cirkel te vermijden. Uit xy = −900 en x + y = −11 volgt
(x − y)2 = (x + y)2 − 4xy = 121 − (−4·900) = 3721
en dus
x − y = 61
Uiteraard is x − y = −61 ook mogelijk, maar aangezien het inverteren van het teken van het verschil van x en y neerkomt op het omwisselen van x en y hebben we aan één waarde voor het verschil genoeg. Nu hebben we
2x = (x + y) + (x − y) = −11 + 61 = 50, dus x = 25
en
2y = (x + y) − (x − y) = −11 − 61 = −72, dus y = −36
Zo kan het dus wel, maar je ziet dat dit toch meer werk is dan het ontbinden van 900 in priemfactoren en even kijken welke combinaties van priemfactoren afvallen.
De strategie om het product van de gezochte grootheden zo ver mogelijk te ontbinden in factoren is ook bruikbaar als de grootheden in kwestie geen concrete getallen zijn. Stel dat je wordt gevraagd om de kwadratische veelterm
2bx2 − (a + b)2x + (a + b)2(a − b)
in de variabele x te ontbinden in lineaire factoren in x (waarbij is gegeven dat dit inderdaad mogelijk is), dan kun je als volgt te werk gaan. We zoeken nu twee grootheden waarvan het product gelijk moet zijn aan 2b(a + b)2(a − b) terwijl de som gelijk moet zijn aan −(a + b)2. Dit lijkt lastig, maar je kunt als volgt redeneren. Het product bevat de factoren
2, b, (a + b), (a + b), (a − b)
en deze vijf factoren moeten we nu verdelen over twee grootheden. Kennelijk bevat elk van de beide gezochte grootheden één factor (a + b), anders zou de som geen factor (a + b) bevatten. Dan moeten we alleen nog de drie resterende factoren 2, b, (a − b) verdelen, en dan is het duidelijk dat we de factoren 2 en b in de ene grootheid moeten stoppen, en de factor (a − b) in de andere grootheid, aangezien 2b + (a − b) = (a + b) en aangezien de som nog een tweede factor (a + b) bevat. De gezochte grootheden zijn dus −(a + b)2b en −(a + b)(a − b) zodat we kunnen schrijven
2bx2 − (a + b)2bx − (a + b)(a − b)x + (a + b)2(a − b)
en dus
2bx·(x − (a + b)) − (a + b)(a − b)·(x − (a + b))
Nu kunnen we de factor (x − (a + b)) buiten haakjes halen en hebben we dus
(2bx − (a + b)(a − b))·(x − (a + b))
en met gebruikmaking van het merkwaardig product (a + b)(a − b) = a2 − b2 is dit nog te schrijven als
(2bx − (a2 − b2))·(x − (a + b))


Ik schaam me om deze vraag te stellen... 
Ik heb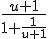 . Ik wil deze breuk versimpelen. Wat ik normaal zou doen is de 1+1/(u+1) versimpelen. Dat maakt
. Ik wil deze breuk versimpelen. Wat ik normaal zou doen is de 1+1/(u+1) versimpelen. Dat maakt 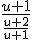 . Maar wat dan? Ik zou zeggen
. Maar wat dan? Ik zou zeggen 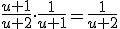 . Dit is echter fout. Kan iemand aanwijzen waar ik de denkfout maak?
. Dit is echter fout. Kan iemand aanwijzen waar ik de denkfout maak?
Ik heb


Het is u + 1 gedeeld door (u+2)/(u + 1),
niet (u+1)/(u+2) gedeeld door u + 1.
Delen door een breuk.. etc
niet (u+1)/(u+2) gedeeld door u + 1.
Delen door een breuk.. etc


Dat was erg dom van me.quote:Op zaterdag 5 juli 2014 12:21 schreef Anoonumos het volgende:
Het is u + 1 gedeeld door (u+2)/(u + 1),
niet (u+1)/(u+2) gedeeld door u + 1.
Delen door een breuk.. etc


Delen door a/b is hetzelfde als vermenigvuldigen met b/a. Maar nog eenvoudiger is hier om teller en noemer van je oorspronkelijke breuk met (u+1) te vermenigvuldigen. In de teller krijg je dan (u+1)² en in de noemer (u+1)+1 = u+2.quote:Op zaterdag 5 juli 2014 12:12 schreef netchip het volgende:
Ik schaam me om deze vraag te stellen...
Ik heb. Ik wil deze breuk versimpelen. Wat ik normaal zou doen is de 1+1/(u+1) versimpelen. Dat maakt
. Maar wat dan? Ik zou zeggen
. Dit is echter fout. Kan iemand aanwijzen waar ik de denkfout maak?


Dit was weer een goed voorbeeld van mijn onnauwkeurigheid op bepaalde momenten.quote:Op zaterdag 5 juli 2014 13:56 schreef Riparius het volgende:
[..]
Delen door a/b is hetzelfde als vermenigvuldigen met b/a. Maar nog eenvoudiger is hier om teller en noemer van je oorspronkelijke breuk met (u+1) te vermenigvuldigen. In de teller krijg je dan (u+1)² en in de noemer (u+1)+1 = u+2.


Wat je schrijft klopt overigens wel, het is hier alleen niet zo bruikbaar om de breuk te vereenvoudigen. Zie je ook waarom?
De notatie voor breuken kan soms verwarrend zijn. Als je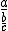 hebt, is het soms lastig te zien of je a/(b/c) bedoelt of (a/b)/c. Kan het zijn dat je daardoor in de war raakt?
hebt, is het soms lastig te zien of je a/(b/c) bedoelt of (a/b)/c. Kan het zijn dat je daardoor in de war raakt?
Als je namelijk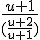 hebt (wat niet hetzelfde is als de breuk die jij probeert te vereenvoudigen) kan je wel gebruiken wat jij nu probeerde.
hebt (wat niet hetzelfde is als de breuk die jij probeert te vereenvoudigen) kan je wel gebruiken wat jij nu probeerde.
Als je in de war raakt, kan je proberen de notatie (a/b) voor breuken te gebruiken (of gewoon haakjes om je breuken te zetten) en je te herinneren dat vermenigvuldigen en delen zich onderling zo gedragen als optellen en aftrekken. Hoewel dit niet helpt bij het vereenvoudigen, dwingt dit je wel de volgorde van de operaties te begrijpen, en is het misschien intuitief iets makkelijker om te begrijpen wat er gebeurt.
Daarnaast: vaak is teller en noemer vermenigvuldigen met hetzelfde getal een trucje wat vaak werkt. Als je ook weet dat (a-b)(a+b) = a^2 - b^2 kan je dit trucje ook gebruiken om breuken waarin teller en noemer ccomplexe getallen zijn te vereenvoudigen.
De notatie voor breuken kan soms verwarrend zijn. Als je
Als je namelijk
Als je in de war raakt, kan je proberen de notatie (a/b) voor breuken te gebruiken (of gewoon haakjes om je breuken te zetten) en je te herinneren dat vermenigvuldigen en delen zich onderling zo gedragen als optellen en aftrekken. Hoewel dit niet helpt bij het vereenvoudigen, dwingt dit je wel de volgorde van de operaties te begrijpen, en is het misschien intuitief iets makkelijker om te begrijpen wat er gebeurt.
Daarnaast: vaak is teller en noemer vermenigvuldigen met hetzelfde getal een trucje wat vaak werkt. Als je ook weet dat (a-b)(a+b) = a^2 - b^2 kan je dit trucje ook gebruiken om breuken waarin teller en noemer ccomplexe getallen zijn te vereenvoudigen.


Ik ben nu bezig met Rudin's Principles of Mathematical Analysis en het maken van de meeste opgaven gaat verbazingwekkend goed. Maar elk hoofdstuk heeft wat vragen die me gewoon maar niet lukken, zoals deze:
https://www.dropbox.com/s/9izr76oi5zd1m58/baby%20rudin.png
Is dit erg? Want op het internet lees ik erg veel tegenstrijdige meningen. De een vindt dat je alle vragen moet doen en dat ze lukken terwijl de ander van mening is dat enkel proberen genoeg is.
En mijn god zeg, wat is dit boek pittig.
https://www.dropbox.com/s/9izr76oi5zd1m58/baby%20rudin.png
Is dit erg? Want op het internet lees ik erg veel tegenstrijdige meningen. De een vindt dat je alle vragen moet doen en dat ze lukken terwijl de ander van mening is dat enkel proberen genoeg is.
En mijn god zeg, wat is dit boek pittig.


Nouja, of dat erg is moet je maar voor jezelf bedenken. Het belangrijkste is denk ik dat je het idee achter de vraag begrijpt. Het is niet zo'n schande als je het bewijs niet kan vinden (al zullen sommigen daar anders over denken). Nu is het natuurlijk ook de vraag wat je precies wil oefenen en hoeveel tijd je hebt, en ook wel hoeveel aanleg je hebt. Ik vind het meestal genoeg om de vragen door te lezen, en de interessante vragen te maken (bijvoorbeeld die waarvan de aanpak niet direct duidelijk is, of die die een techniek vereisen die ik wil oefenen).quote:Op maandag 7 juli 2014 16:28 schreef Novermars het volgende:
Ik ben nu bezig met Rudin's Principles of Mathematical Analysis en het maken van de meeste opgaven gaat verbazingwekkend goed. Maar elk hoofdstuk heeft wat vragen die me gewoon maar niet lukken, zoals deze:
https://www.dropbox.com/s/9izr76oi5zd1m58/baby%20rudin.png
Is dit erg? Want op het internet lees ik erg veel tegenstrijdige meningen. De een vindt dat je alle vragen moet doen en dat ze lukken terwijl de ander van mening is dat enkel proberen genoeg is.
En mijn god zeg, wat is dit boek pittig.


Neem er de tijd voor. Maak iedere dag een opgave, en zorg dat je bewijs ook juist is.quote:Op maandag 7 juli 2014 16:28 schreef Novermars het volgende:
Ik ben nu bezig met Rudin's Principles of Mathematical Analysis en het maken van de meeste opgaven gaat verbazingwekkend goed. Maar elk hoofdstuk heeft wat vragen die me gewoon maar niet lukken, zoals deze:
https://www.dropbox.com/s/9izr76oi5zd1m58/baby%20rudin.png
Is dit erg? Want op het internet lees ik erg veel tegenstrijdige meningen. De een vindt dat je alle vragen moet doen en dat ze lukken terwijl de ander van mening is dat enkel proberen genoeg is.
En mijn god zeg, wat is dit boek pittig.
Het is absoluut geen schande als analyse soms niet lukt.


Hoe zit het met 'complexe' exponenten? Als je de identiteit van Euler hebt, 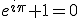 , hoe kan je e dan verheffen tot de macht i maal pi?
, hoe kan je e dan verheffen tot de macht i maal pi?


Met deze formulequote:Op woensdag 9 juli 2014 17:53 schreef netchip het volgende:
Hoe zit het met 'complexe' exponenten? Als je de identiteit van Euler hebt,, hoe kan je e dan verheffen tot de macht i maal pi?
Euler's formule
Zo heb je ook de complexe logarithme
log z = Log |z| + i arg z, waar Log the logarithme voor positieve getallen is.
en arg alle mogelijke argumenten van z.
[ Bericht 5% gewijzigd door t4rt4rus op 09-07-2014 18:07:39 ]


Dit is een beetje vage vraag zo.quote:Op woensdag 9 juli 2014 17:53 schreef netchip het volgende:
Hoe zit het met 'complexe' exponenten? Als je de identiteit van Euler hebt,, hoe kan je e dan verheffen tot de macht i maal pi?
Ik neem aan dat je de waarde van e tot de macht i maal pi wil weten? Kijk eens naar die formule: daarin is e al tot de macht i maal pi genomen.
Als je meer in het algemeen bedoelt hoe men aan deze waarde is gekomen, dan zijn er verschillende manieren. Misschien de makkelijkste is om naar machtreeks ontwikkelingen voor e, sinus en cosinus te kijken. Ik ga dat niet hier uittypen, als het je interesseert kan je googlen of wolfram alhpa gebruiken om de taylorreeksen van e^x, sinus en cosinus op te zoeken, en de machtreeks van e^x te bekijken als je bijvoorbeeld x = iy substitueert, en gebruikt dat
i^2 = i^6 = ... = -1
i^3 = i^7 = ... = -i
i^4 = i^8 = ... = 1
i^5 = i^9 = ... = i
Daarnaast is er nog een wat inzichtelijkere manier, die Riparius een keer heeft uitgelegd en die gebruiktmaakt van een geometrische interpretatie (maar hiervoor moet je wel de geometrische interpretaties van complexe getallen en hun producten kennen).


Ah, OK. Hoe zou ikquote:Op woensdag 9 juli 2014 18:00 schreef t4rt4rus het volgende:
[..]
Met deze formule
[ afbeelding ]
Euler's formule
Zo heb je ook de complexe logarithme
log z = Log |z| + i arg z, waar Log the logarithme voor positieve getallen is.
en arg alle mogelijke argumenten van z.
Hier zou ik naar kunnen kijken; alhoewel dit wel een beetje buiten mijn kunnen ligt, denk ik.quote:Op woensdag 9 juli 2014 18:09 schreef defineaz het volgende:
[..]
Dit is een beetje vage vraag zo.
Ik neem aan dat je de waarde van e tot de macht i maal pi wil weten? Kijk eens naar die formule: daarin is e al tot de macht i maal pi genomen.
Als je meer in het algemeen bedoelt hoe men aan deze waarde is gekomen, dan zijn er verschillende manieren. Misschien de makkelijkste is om naar machtreeks ontwikkelingen voor e, sinus en cosinus te kijken. Ik ga dat niet hier uittypen, als het je interesseert kan je googlen of wolfram alhpa gebruiken om de taylorreeksen van e^x, sinus en cosinus op te zoeken, en de machtreeks van e^x te bekijken als je bijvoorbeeld x = iy substitueert, en gebruikt dat
i^2 = i^6 = ... = -1
i^3 = i^7 = ... = -i
i^4 = i^8 = ... = 1
i^5 = i^9 = ... = i
Daarnaast is er nog een wat inzichtelijkere manier, die Riparius een keer heeft uitgelegd en die gebruiktmaakt van een geometrische interpretatie (maar hiervoor moet je wel de geometrische interpretaties van complexe getallen en hun producten kennen).
Wanneer weet je of dat je aanleg hebt voor wiskunde? Mensen nemen vaak aan: hoog cijfer voor wiskunde -> talent. Dat geloof ik niet 100%. Ik ben namelijk benieuwd hoe het met mij zit. Ik zal even wat achtergrond informatie geven. Ik zit in 3 vwo (na de zomervakantie 4 vwo), heb plezier in wiskunde en sta er dan ook een goed cijfer voor. In mijn vrije tijd ben ik bezig met het lezen van een calculus boek en het maken van opdrachten. Dit gaat mij vrij goed af. Ik hoef voor het 'gewone' boek (Getal en Ruimte) ook nauwelijks moeite te doen, ik snap het in een keer. Het bewijzen van stellingen gaat ongeveer zo bij mij:
Interpreteer deze vraag niet als arrogantie, of zoiets. Ik ben oprecht benieuwd naar of dat ik nu een hoog cijfer haal door mijn interesse, of doordat ik aanleg heb.


Achten zonder te leren haal je door aanleg. Alles daarboven komt door interesse én hard werken.
Verder is WA perfect om dingen te berekenen: http://www.wolframalpha.com/input/?i=5%5E%285i%29
Probeer maar eens uit te leggen dat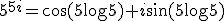
Verder is WA perfect om dingen te berekenen: http://www.wolframalpha.com/input/?i=5%5E%285i%29
Probeer maar eens uit te leggen dat


Is die 5log(5) bedoelt als 5log(5) of als 5ln(5)?quote:Op woensdag 9 juli 2014 20:37 schreef Novermars het volgende:
Achten zonder te leren haal je door aanleg. Alles daarboven komt door interesse én hard werken.
Verder is WA perfect om dingen te berekenen: http://www.wolframalpha.com/input/?i=5%5E%285i%29
Probeer maar eens uit te leggen dat
Leren voor wiskunde heb ik nooit gedaan. Een half uurtje serieus werken in de les is genoeg om het huiswerk af te hebben.


Probeer daar eens zelf uit te komen.quote:Op woensdag 9 juli 2014 20:54 schreef netchip het volgende:
[..]
Is die 5log(5) bedoelt als 5log(5) of als 5ln(5)?
Leren voor wiskunde heb ik nooit gedaan. Een half uurtje serieus werken in de les is genoeg om het huiswerk af te hebben.
Hele dikke hint is het gene waar 5log5 in staat.


Oh joh, ik dacht dat je al aan het studeren wasquote:Op woensdag 9 juli 2014 20:54 schreef netchip het volgende:
[..]
Is die 5log(5) bedoelt als 5log(5) of als 5ln(5)?
Leren voor wiskunde heb ik nooit gedaan. Een half uurtje serieus werken in de les is genoeg om het huiswerk af te hebben.
Bij wiskunde wordt meestal de 'natuurlijke logaritme' bedoeld, die op de middelbare school met ln wordt genoteerd. In dit geval is dat ook zo. Probeer eens te bedenken hoe je 5^x om kan schrijven in de vorm e^y, dan ben je al een heel eind
Welk calculusboek ben je aan het lezen? Ik vind het altijd wel apart dat calculus in de VS als het summum van de wiskunde wordt gezien, terwijl de ideeën erachter echt heel erg elementair zijn vergeleken met veel andere wiskunde


Ik denk dat het misschien wel beter is als hij iets van discrete wiskunde/grafentheorie/lineaire algebra gaat doen in plaats van calculus.quote:Op woensdag 9 juli 2014 21:00 schreef defineaz het volgende:
[..]
Oh joh, ik dacht dat je al aan het studeren was
Bij wiskunde wordt meestal de 'natuurlijke logaritme' bedoeld, die op de middelbare school met ln wordt genoteerd. In dit geval is dat ook zo. Probeer eens te bedenken hoe je 5^x om kan schrijven in de vorm e^y, dan ben je al een heel eind
Welk calculusboek ben je aan het lezen? Ik vind het altijd wel apart dat calculus in de VS als het summum van de wiskunde wordt gezien, terwijl de ideeën erachter echt heel erg elementair zijn vergeleken met veel andere wiskunde
Calculus is veelal het toepassen van een stappenplan, terwijl de dingen die ik net opnoemde misschien wel veel beter zijn om een wiskundetalent te ontkiemen.


Ben nog bezig met het volledig uitdenken, dit is wat ik tot nu toe heb:quote:Op woensdag 9 juli 2014 20:37 schreef Novermars het volgende:
Achten zonder te leren haal je door aanleg. Alles daarboven komt door interesse én hard werken.
Verder is WA perfect om dingen te berekenen: http://www.wolframalpha.com/input/?i=5%5E%285i%29
Probeer maar eens uit te leggen dat
Ik heb het gevoel dat ik iets mis. Het meest logische zou zijn dat de rekenregels voor complexe getallen niet hetzelfde zijn als voor de reele getallen.
[ Bericht 3% gewijzigd door netchip op 09-07-2014 21:38:49 ]


de log is een natuurlijk logarithme niet 5log.quote:Op woensdag 9 juli 2014 21:33 schreef netchip het volgende:
[..]
Ben nog bezig met het volledig uitdenken, dit is wat ik tot nu toe heb:. Bij mijn voorbeeld 55i is x is 5.
. Die 5log kan je dan omrekenen door te doen: ln(5)/ln(5).
Ik heb het gevoel dat ik iets mis. Het meest logische zou zijn dat de rekenregels voor complexe getallen niet hetzelfde zijn als voor de reele getallen.
5 log 5 is dus 5 * log 5
