h staat voor hoogte van de bal
a staat voor afstand van de bal
de bal komt op de grond bij a=96.
bereken op welke afstand de bal op maximale hoogte is.
Ik heb hier ingeklemt en ik kwam uit op de goeie antwoord, namelijk a=46, maar hoezo moet ik bij de eerste A -0.012(46)^2 doen en niet -0.012x46^2 of -0.012x(46)^2
Inklemmen
Dit.quote:Op dinsdag 13 mei 2014 22:04 schreef ludicrous_monk het volgende:
ff de functie differentieren en gelijk stellen aan nul, klaar is kees.
Inklemmen
[ Bericht 50% gewijzigd door ulq op 13-05-2014 22:07:12 ]
Ja, en tenzij je een telraam gebruikt zou je rekenmachine moeten weten dat machtsverheffingen voor vermenigvuldigen komenquote:
Misschien snap ik het niet helemaal maar -0.012(46)^2 = -0.012x46^2 = -0.012x(46)^2 toch?
Not sure if...quote:
Heb het even gegoogeld. Pinguin methode noemde mijn wiskundeleraar dat op de middelbare school.quote:
Wtf man, waarom pinguïns?quote:Op dinsdag 13 mei 2014 22:13 schreef thenxero het volgende:
[..]
Heb het even gegoogeld. Pinguin methode noemde mijn wiskundeleraar dat op de middelbare school.
Heb het ook nooit begrepen. Pinguïns bewegen zich altijd een beetje lomp voort. Beetje de lompe methode. Misschien is dat hetquote:
.Klinkt best wel logisch eigenlijk.quote:
[..]
Heb het ook nooit begrepen. Pinguïns bewegen zich altijd een beetje lomp voort. Beetje de lompe methode. Misschien is dat het
quote:
[..]
Heb het ook nooit begrepen. Pinguïns bewegen zich altijd een beetje lomp voort. Beetje de lompe methode. Misschien is dat het
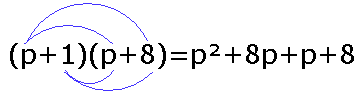
En dit de papegaaienbek methode
Lijkt meer op de schaar van een kreeft zo.
En dan heb je ook nog snavelbekfigurenquote:Op dinsdag 13 mei 2014 22:19 schreef Anoonumos het volgende:
[..]
[ afbeelding ]
En dit de papegaaienbek methode
Lijkt meer op de schaar van een kreeft zo.
Ik heb ook werkelijk nog nooit van inklemmen gehoord...quote:
De natte-vinger-methode klinkt niet zo netjes. Maar het komt wel op hetzelfde neer.quote:Op dinsdag 13 mei 2014 22:23 schreef JoPiDo het volgende:
[..]
Ik heb ook werkelijk nog nooit van inklemmen gehoord...
quote:
[..]
De natte-vinger-methode klinkt niet zo netjes. Maar het komt wel op hetzelfde neer.
het is erg simpel, zoveel mogelijk op je rekenmachine intikken tot dat je op het goeie antwoord komt.quote:
[..]
Ik heb ook werkelijk nog nooit van inklemmen gehoord...
Differentiëren en gelijkstellen aan 0 is makkelijker.quote:
[..]
het is erg simpel, zoveel mogelijk op je rekenmachine intikken tot dat je op het goeie antwoord komt.
Het is een dom omslachtig trucje.quote:
[..]
het is erg simpel, zoveel mogelijk op je rekenmachine intikken tot dat je op het goeie antwoord komt.
Maar het werkt wel.quote:
Bij dit soort simpele formules wel ja. Maar differentiëren is sneller.quote:
Kan je het even voor doen?quote:Op dinsdag 13 mei 2014 23:03 schreef Rezania het volgende:
[..]
Bij dit soort simpele formules wel ja. Maar differentiëren is sneller.
Vraag dat maar aan je docent.quote:
Afgeleide van -0.012 x a^2 + 1.152 x a=
[-0.012a^2+1.152]'= 2*-0.012a+1.152= -0.024a+1.152
Afgeleide gelijkstellen aan 0:
-0.024a+1.152=0
-0.024a=-1.152
24a=1152
a=1152/24=48
Niet 46 dus...
OK.quote:
Is dit de snelle manier?quote:
Daar waar de afgeleide 0 is, is de bal niet meer aan het stijgen en nog net niet aan het dalen, dus dat is het hoogste punt.
Afgeleide van -0.012 x a^2 + 1.152 x a=
[-0.012a^2+1.152]'= 2*-0.012a+1.152= -0.024a+1.152
Afgeleide gelijkstellen aan 0:
-0.024a+1.152=0
-0.024a=-1.152
24a=1152
a=1152/24=48
Niet 46 dus...
Bedankt voor de uitleg btw.
Nee, het kan nog veel sneller als je even nadenkt. Inklemmen of differentiëren zijn hier volmaakt overbodig.quote:
[..]
Is dit de snelle manier?
Bedankt voor de uitleg btw.
Gegeven is dat H = 0 voor a = 96 en je ziet ook direct dat H = 0 voor a = 0. Aangezien de grafiek van H als functie van a een bergparabool is wordt het maximum bereikt op de helft van het interval [0, 96], dus voor a = 96/2 = 48.
Dan moet je wel eerst nog even checken dat ook voor a=96 het waar is dat H=0; de grond had ook hoger of lager dan 0 kunnen zitten. Zodra je weet dat voor zowel a=96 H=0 en a=0 H=0 dan kan je, wetend dat het een parabool is, inderdaad delen door 2. De manier met 'afgeleide=0' werkt altijd, ook als er had gestaan dat hij de grond raakt bij a=92 of a=98, of welke andere waarde van a ook mits a>48. De grond hoeft dan ook niet recht te zijn.quote:
[..]
Nee, het kan nog veel sneller als je even nadenkt. Inklemmen of differentiëren zijn hier volmaakt overbodig.
Gegeven is dat H = 0 voor a = 96 en je ziet ook direct dat H = 0 voor a = 0. Aangezien de grafiek van H als functie van a een bergparabool is wordt het maximum bereikt op de helft van het interval [0, 96], dus voor a = 96/2 = 48.
Dus 2 manieren:
1) a=96 en a=0 invullen in de normale formule, als dan H=0 voor beide dan 96/2=48, anders alsnog methode 2
2) Afgeleide gelijk aan 0 en dan a bepalen.
Zelf vind ik 2 makkelijker, aangezien het kwadraat van 96 dan meteen verdwijnt en je het dan zonder rekenmachine kan doen; methode 1 zonder rekenmachine is lastig om a=96 te checken.
[ Bericht 13% gewijzigd door Sannr_ op 14-05-2014 07:58:09 ]
Ja, maar nu ga je extra aannames doen die niet uit de opgave zoals die in de OP wordt weergegeven zijn af te leiden. Dat H = 0 voor a = 96 was kennelijk in de opgave gegeven. Wellicht werd er in de oorspronkelijke opgave gevraagd om dit ook met de rekenmachine te controleren. Je hoeft mij niet te vertellen dat differentiaalrekening altijd bruikbaar is. Maar TS weet gezien de opleiding die hij volgt waarschijnlijk niets van differentiaalrekening, en dat is iets waar alle anderen die in dit topic hebben gereageerd, ook jij, niet bij stil hebben gestaan. Daarom denk ik dat het inderdaad de bedoeling was van de opgave om de leerling zich te laten realiseren dat de (parabool)baan die de bal beschrijft een verticale symmetrie-as heeft, zodat het hoogste punt wordt bereikt op de helft van de afstand. En dat kan de leerling dan uiteraard weer verifiëren met zijn rekenmachine.quote:
[..]
Dan moet je wel eerst nog even checken dat ook voor a=96 het waar is dat H=0; de grond had ook hoger of lager dan 0 kunnen zitten. Zodra je weet dat voor zowel a=96 H=0 en a=0 H=0 dan kan je, wetend dat het een parabool is, inderdaad delen door 2. De manier met 'afgeleide=0' werkt altijd, ook als er had gestaan dat hij de grond raakt bij a=92 of a=98, of welke andere waarde van a ook mits a>48. De grond hoeft dan ook niet recht te zijn.
Nee nee, jij doet juist extra aannames, door te stellen dat de grond zit op H=0, terwijl dat ook alleen een nulpunt van een werpende hand kan zijn (en de grond dan lager is bijvoorbeeld), en dat de grond recht is. In de opgave staat alleen dat ie op a=96 land, maar of dat op H=0 is moet je juist nog checken. Ik doe juist geen extra aannames over de situatie, dat is juist mijn punt.quote:
[..]
Ja, maar nu ga je extra aannames doen die niet uit de opgave zoals die in de OP wordt weergegeven zijn af te leiden. Dat H = 0 voor a = 96 was kennelijk in de opgave gegeven. Wellicht werd er in de oorspronkelijke opgave gevraagd om dit ook met de rekenmachine te controleren. Je hoeft mij niet te vertellen dat differentiaalrekening altijd bruikbaar is. Maar TS weet gezien de opleiding die hij volgt waarschijnlijk niets van differentiaalrekening, en dat is iets waar alle anderen die in dit topic hebben gereageerd, ook jij, niet bij stil hebben gestaan. Daarom denk ik dat het inderdaad de bedoeling was van de opgave om de leerling zich te laten realiseren dat de (parabool)baan die de bal beschrijft een verticale symmetrie-as heeft, zodat het hoogste punt wordt bereikt op de helft van de afstand. En dat kan de leerling dan uiteraard weer verifiëren met zijn rekenmachine.
Nee, in de opgave staat niet dat de hoogte van het punt waar de bal weer de grond raakt verschilt van de hoogte van het punt boven de grond waar de bal aan zijn baan begint. Maar het staat wel vast dat je H = 0 hebt voor a = 0 en tevens voor H = 0 voor a = 96. Zoals ik al aan heb gegeven staat er in de oorspronkelijke opgave hoogstwaarschijnlijk dat de leerling dat laatste gegeven eerst moet controleren aan de hand van de gegeven formule. En dan is het evident dat H een maximum bereikt voor a = 96/2 = 48.quote:
[..]
Nee nee, jij doet juist extra aannames, door te stellen dat de grond zit op H=0, terwijl dat ook alleen een nulpunt van een werpende hand kan zijn (en de grond dan lager is bijvoorbeeld), en dat de grond recht is. In de opgave staat alleen dat ie op a=96 land, maar of dat op H=0 is moet je juist nog checken. Ik doe juist geen extra aannames over de situatie, dat is juist mijn punt.
Er staat niet dat het zo is, noch dat het wel zo is. Je kunt er dus geen aannames over doenquote:
Nee, in de opgave staat niet dat de hoogte van het punt waar de bal weer de grond raakt verschilt van de hoogte van het punt boven de grond waar de bal aan zijn baan begint.
Nee, alleen dat hij de grond raakt voor a =96, op welke hoogte de grond daar zit, en waar de bal is voor a = 0 staat nergens, dat moet je uit de formule halen door narekenenquote:Maar het staat wel vast dat je H = 0 hebt voor a = 0 en tevens voor H = 0 voor a = 96
Precies, maar die aannames deed ik dan ook niet. Lees nog maar even goed wat ik hierboven schrijf voordat jij reageerde. Jij was degene die bezwaar maakte tegen mijn eenvoudige oplossing door erop te wijzen dat de plaats waar de bal weer op de grond neerkomt ook hoger of lager kan liggen. Maar dat is hier niet aan de orde.quote:
[..]
Er staat niet dat het zo is, noch dat het wel zo is. Je kunt er dus geen aannames over doen
Natuurlijk zie je direct dat H = 0 voor a = 0 en moet worden geverifieerd dat H = 0 voor a = 96, maar de opgave suggereert al dat dat zo is. En dan heb je geen differentiaalrekening of inklemmen nodig om direct te weten dat H maximaal is voor a = 48. Dat is het punt dat ik maakte en daar is niets op af te dingen.quote:[..]
Nee, alleen dat hij de grond raakt voor a = 96, op welke hoogte de grond daar zit, en waar de bal is voor a = 0 staat nergens, dat moet je uit de formule halen door narekenen.
Het is uiteindelijk misschien niet aan de orde, maar voor je wist of je antwoord klopte moest je dat wel eerst nog verifiëren. De opgave 'suggereert' betekent nog niet dat je het niet meer hoeft na te gaan. En mijn punt is dat dan alleen de afgeleide nemen en invullen makkelijker is (en zelfs zonder rekenmachine kan).quote:
[..]
Precies, maar die aannames deed ik dan ook niet. Lees nog maar even goed wat ik hierboven schrijf voordat jij reageerde. Jij was degene die bezwaar maakte tegen mijn eenvoudige oplossing door erop te wijzen dat de plaats waar de bal weer op de grond neerkomt ook hoger of lager kan liggen. Maar dat is hier niet aan de orde.
[..]
Natuurlijk zie je direct dat H = 0 voor a = 0 en moet worden geverifieerd dat H = 0 voor a = 96, maar de opgave suggereert al dat dat zo is. En dan heb je geen differentiaalrekening of inklemmen nodig om direct te weten dat H maximaal is voor a = 48. Dat is het punt dat ik maakte en daar is niets op af te dingen.
TS reageert niet meer, en hij heeft geen scan van de originele opgave gepost, dus wat daar precies in stond moet ik in het midden laten. Maar het is duidelijk een opgave waarbij de rekenmachine moest worden gebruikt. Kijk verder de postgeschiedenis van TS maar even door, dan weet je dat hij een opleiding doet waarbij differentiëren niet aan de orde komt, dus daar weet hij niets van. Hij heeft dan ook niets aan mensen die aan komen zetten met het bepalen van een afgeleide en stellen dat dat makkelijker is, dat is het voor hem zeker niet. Sterker nog, ik denk dat het volkomen abracadabra voor hem is. Je ziet trouwens in zijn OP dat hij, met rekenmachine en al, kennelijk niet eens in staat is om H uit te rekenen voor a = 46.quote:
[..]
Het is uiteindelijk misschien niet aan de orde, maar voor je wist of je antwoord klopte moest je dat wel eerst nog verifiëren. De opgave 'suggereert' betekent nog niet dat je het niet meer hoeft na te gaan. En mijn punt is dat dan alleen de afgeleide nemen en invullen makkelijker is (en zelfs zonder rekenmachine kan).