SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Ik snap niet of dat gewoon 2 punten zijn of dat het 2 lijnen zijn? En wat is die h?quote:
En waarvoor staat eigenlijk die x in f(x) ? Stel je hebt f(2) = 2x is het dan 2*2? Of is het 2x = 2?
Een beknopt overzichtje vind je op de oude formulekaart van het VWO.quote:Op vrijdag 9 mei 2014 22:38 schreef RustCohle het volgende:
[..]
Aha! Dat is dus wat ik zocht die f'(x) = nxn−1
Ken je een goede website met dit soort regels en uitleg mbt differentieren?
En goede websites ken ik ook wel maar die zijn voor jou gezien je gebrek aan voorkennis (algebra e.d.) gewoon te moeilijk. Maar wellicht kun je de Nederlandse Wikipedia te raadplegen. Verder denk ik dat het niet zoveel zin heeft voor jou. Je bent nu paniekvoetbal aan het spelen, dit gaat niets worden. Niet omdat het moeilijk zou zijn, dat is het niet. Iedereen met een normale intelligentie is in staat wiskunde op VWO niveau onder de knie te krijgen, maar dat gaat niet zomaar. Daarvoor heb je echt goed onderwijs nodig, met goede leerboeken en goede docenten die ook echt les geven, en veel tijd. Allemaal zaken waaraan het in Nederland in het algemeen ontbreekt en die jij nu in ieder geval al helemaal niet tot je beschikking hebt.
Die formule is gewoon delta y / delta x.quote:
[..]
Ik snap niet of dat gewoon 2 punten zijn of dat het 2 lijnen zijn? En wat is die h?
Ik zal je beloven dat ik een voldoende resultaat zal behalen voor de toets. Wellicht geen 10, maar wel een goed resultaat. Ik ben inderdaad paniekerig, maar wel overtuigd van mijn doorzettingsvermogen.quote:
[..]
Een beknopt overzichtje vind je op de oude formulekaart van het VWO.
En goede websites ken ik ook wel maar die zijn voor jou gezien je gebrek aan voorkennis (algebra e.d.) gewoon te moeilijk. Maar wellicht kun je de Nederlandse Wikipedia te raadplegen. Verder denk ik dat het niet zoveel zin heeft voor jou. Je bent nu paniekvoetbal aan het spelen, dit gaat niets worden. Niet omdat het moeilijk zou zijn, dat is het niet. Iedereen met een normale intelligentie is in staat wiskunde op VWO niveau onder de knie te krijgen, maar dat gaat niet zomaar. Daarvoor heb je echt goed onderwijs nodig, met goede leerboeken en goede docenten die ook echt les geven, en veel tijd. Allemaal zaken waaraan het in Nederland in het algemeen ontbreekt en die jij nu in ieder geval al helemaal niet tot je beschikking hebt.
Ik heb 20.1 t/m 20.8 geheel foutloos gemaakt, op 1 opgave na, en dat vind ik al knap van mijzelf, terwijl ik gister nog keek alsof ik water zag branden.
Deze is wellicht een pittige:
√2x
Hoe differentieer ik dit?
Ik zelf dacht aan 2^(1/2) * x^(1/2) = 2x^1 = 2
Echter klopt hier geen zak van.
Ik ben mij bovendien wel van bewust dat √2x gelijk is aan √2 * √x
√2x
Hoe differentieer ik dit?
Ik zelf dacht aan 2^(1/2) * x^(1/2) = 2x^1 = 2
Echter klopt hier geen zak van.
Ik ben mij bovendien wel van bewust dat √2x gelijk is aan √2 * √x
Denk aan de standaard formulequote:
Deze is wellicht een pittige:
√2x
Hoe differentieer ik dit?
Ik zelf dacht aan 2^(1/2) * x^(1/2) = 2x^1 = 2
Echter klopt hier geen zak van.
Ik ben mij bovendien wel van bewust dat √2x gelijk is aan √2 * √x
Dan moet je je eigen post nog eens terug lezen.quote:
-edit- overigens is
Aha!quote:
[..]
Dan moet je je eigen post nog eens terug lezen.
-edit- overigens isen niet 1. (maar dat is nogsteeds het verkeerde antwoord)
Wel vaag.. Ik kan het nu wel... differentieren, iig de zeer basic differentieren, maar toch begrijp ik heel de dotatie van (c f(x))' = x f'(x)
en (f(x) + g(x))' = f' (x) + g'(x) nog steeds niet
Opgave 20.1 t/m 20.9 foutloos , op 1 vraag na!!
Ik ben ongelofelijk happy! Het is de basis en de basis is toch enorm belangrijk.
Daar klopt inderdaad niet veel van. Tip: √2 is een constante, √x kan gewoon met de machtsregel.quote:
Deze is wellicht een pittige:
√2x
Hoe differentieer ik dit?
Ik zelf dacht aan 2^(1/2) * x^(1/2) = 2x^1 = 2
Echter klopt hier geen zak van.
Ik ben mij bovendien wel van bewust dat √2x gelijk is aan √2 * √x
Volgensmij gaat ie daar differentieren, dus goed maar foutquote:
[..]
Dan moet je je eigen post nog eens terug lezen.
-edit- overigens is
.
Er zijn allemaal verschillende notaties voor differentiatie.quote:
[..]
Aha!
Wel vaag.. Ik kan het nu wel... differentieren, iig de zeer basic differentieren, maar toch begrijp ik heel de dotatie van (c f(x))' = x f'(x)
en (f(x) + g(x))' = f' (x) + g'(x) nog steeds niet
Opgave 20.1 t/m 20.9 foutloos , op 1 vraag na!!
Ik ben ongelofelijk happy! Het is de basis en de basis is toch enorm belangrijk.
f' betekent gewoon de afgeleide van f
(c f(x))' betekent afgeleide van c f(x), of
g(x) = c f(x), dan is de afgeleide van g: g'(x) = (c f(x))'
(deze afgeleide is trouwens c f'(x), niet x f'(x))
Voor het aangeven dat je de afgeleide van f bedoeld is f' wel handig, anders vind ik hem zelf een beetje onduidelijk.
Maar er zijn ook andere notaties zoals
Hier in geef je dus ook aan waar je naar differentieert. Wat je bij de f' notatie niet doet.
-edit-
Wat heb je trouwens als uitkomst van
Je kunt dit op verschillende manieren aanpakken. Van belang is in ieder geval dat je begrijpt dat √a ook is te schrijven als a1/2, immers (a1/2)2 = a(1/2)·2 = a1 = a.quote:
Deze is wellicht een pittige:
√2x
Hoe differentieer ik dit?
Je kunt schrijven
√2x = √2·√x = 21/2·x1/2
Maar ook
√2x = (2x)1/2
Bepaal nu in beide gevallen de afgeleide met behulp van bekende regels voor het differentiëren (in het tweede geval moet je de kettingregel gebruiken). Uiteraard moet je in beide gevallen op hetzelfde uitkomen.
Ik heb een opdracht waarbij ik de 2e afgeleide moet bepalen.
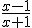
Als ik de eerste afgeleide bereken kom ik op:
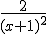
Maar dan dus naar de 2e afgeleide:
Ik kom tot:
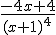
Maar het antwoord is:
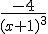
Is mijn antwoord nog te vereenvoudigen of heb ik al eerder een afslag gemist?
Als ik de eerste afgeleide bereken kom ik op:
Maar dan dus naar de 2e afgeleide:
Ik kom tot:
Maar het antwoord is:
Is mijn antwoord nog te vereenvoudigen of heb ik al eerder een afslag gemist?
2(x+1)-2 heeft als afgeleide -4(x+1)-3
Geen quotientregel voor nodig (die je verkeerd hebt gedaan de tweede keer, haakjes verkeerd gezet?)
f(x) = 2
g(x) = (x+1)2
f'(x) g(x) - f(x) g'(x) = 0 · (x+1)2 - 2 · 2(x+1) = -4(x+1)
[ Bericht 27% gewijzigd door Anoonumos op 10-05-2014 00:02:36 ]
Geen quotientregel voor nodig (die je verkeerd hebt gedaan de tweede keer, haakjes verkeerd gezet?)
f(x) = 2
g(x) = (x+1)2
f'(x) g(x) - f(x) g'(x) = 0 · (x+1)2 - 2 · 2(x+1) = -4(x+1)
[ Bericht 27% gewijzigd door Anoonumos op 10-05-2014 00:02:36 ]
Thanks, niet bij nagedacht dat ik de breuk kon wegwerken. Ik heb idd die laatste regel van jouw post gedaan.quote:
2(x+1)-2 heeft als afgeleide -4(x+1)-3
Geen quotientregel voor nodig (die je verkeerd hebt gedaan de tweede keer, haakjes verkeerd gezet?)
f(x) = 2
g(x) = (x+1)2
f'(x) g(x) - f(x) g'(x) = 0 · (x+1)2 - 2 · 2(x+1) = -4(x+1)
Als je gebruik van de quotiëntregel kunt vermijden (zoals hier), dan is het verstandig dat ook te doen.quote:Op zaterdag 10 mei 2014 00:07 schreef nodig het volgende:
[..]
Thanks, niet bij nagedacht dat ik de breuk kon wegwerken. Ik heb idd die laatste regel van jouw post gedaan.
En nog een tip: je hebt
(x − 1)/(x + 1) = (x + 1 − 2)/(x + 1) = 1 − 2/(x + 1) = 1 − 2·(x + 1)−1
zodat je ook voor de bepaling van de eerste afgeleide de quotiëntregel niet nodig hebt.
[ Bericht 17% gewijzigd door Riparius op 10-05-2014 00:22:59 ]
√2 toch een constante ? Ondanks de exponent?quote:
[..]
Daar klopt inderdaad niet veel van. Tip: √2 is een constante, √x kan gewoon met de machtsregel.
Ja, dus wat komt er uit?quote:
[..]
√2 toch een constante ? Ondanks de exponent?
quote:
Wat is de basis voor het differentieren van 1/x? Dus gewoon deelsommen?
En dan weer die ene standaard regel toepassen.
-x-² dusquote:
[..]
En dan weer die ene standaard regel toepassen.
5 / x^5quote:
[..]
En dan weer die ene standaard regel toepassen.
dit doe je toch als volgt:
die x^5 is hetzelfde als 5x en dan wordt het 5/ 5x en dan
5x^-5 en dus -25x^-6?
Correctquote:
Je beschrijving klopt voor geen meter, lees die nog eens na.quote:
[..]
5 / x^5
dit doe je toch als volgt:
die x^5 is hetzelfde als 5x en dan wordt het 5/ 5x en dan
5x^-5 en dus -25x^-6?
(Overigens ben ik er zelf ook een van die veel te snel iets typt en zendt zonder na te lezen. (zie paar posts terug...))
Gebruik standaard regel
√x / x
Ik deed:
1x ^x ^(-1/2) = 1x^(-1/2)x^(-3/2) = -1/2 ^(-5/2)x^(-3/2)
Ik doe iets fout want het is.. -1/2^x^(-3/2)
Ik deed:
1x ^x ^(-1/2) = 1x^(-1/2)x^(-3/2) = -1/2 ^(-5/2)x^(-3/2)
Ik doe iets fout want het is.. -1/2^x^(-3/2)
Je doet echter toch hetzelfde? Welke wordt 5x eigenlijk? die van de exponent toch?quote:
[..]
Correct
[..]
Je beschrijving klopt voor geen meter, lees die nog eens na.
(Overigens ben ik er zelf ook een van die veel te snel iets typt en zendt zonder na te lezen. (zie paar posts terug...))
[tex]f(x) = \frac{5}{x^5} = 5 x^{-5}[/tex]
Gebruik standaard regel
Misschien doe je hetzelfde, maar je beschrijving is totaal onduidelijk.quote:
[..]
Je doet echter toch hetzelfde? Welke wordt 5x eigenlijk? die van de exponent toch?
Hetzelfde hier
Dit moet je veel duidelijker beschrijven, dan maak je ook minder fouten.quote:
√x / x
Ik deed:
1x ^x ^(-1/2) = 1x^(-1/2)x^(-3/2) = -1/2 ^(-5/2)x^(-3/2)
Ik doe iets fout want het is.. -1/2^x^(-3/2)
Want wat bedoel je met 1x^x^(-1/2)?
En je schrijft ook nergens op waar je de differentiatie stap doet.
Je kan
En dan kom je er denk ik zelf wel uit.
Wat je hier doet is niet netjes en zou ik dan ook fout rekenen, hoewel de uitkomst correct is. Maar het gaat evengoed om het hanteren van de juiste methode. Je maakt hier een denkfout. Je krijgt bij differentiëren van je primitieve op grond van de kettingregel een extra factor 2 die je niet wil hebben, en die compenseer je door te delen door d(2x)/dx = 2. Dat gaat hier goed omdat deze afgeleide een constante is, maar in het algemeen werkt deze aanpak niet: als F een primitieve is van f dan is F(g(x))/g'(x) in het algemeen geen primitieve van f(g(x)), maar jij lijkt te denken dat dat wel zo is. Dat verraadt dat je het inderdaad nog niet begrijpt.quote:
[..]
[..]
oh ik ben er al uit, alhoewel de fundamenten van de onderstaande niet helemaal begrijp, maar dat is nu niet zo heel belangrijk.
het boek stelt: [ afbeelding ]
dus is dit mijn uitwerking
[ afbeelding ]
Is dat omdat je die x kan wegstrepen? Maar waarom kan die wortel opeens in de noemer staan?quote:
[..]
Misschien doe je hetzelfde, maar je beschrijving is totaal onduidelijk.
Hetzelfde hier
[..]
Dit moet je veel duidelijker beschrijven, dan maak je ook minder fouten.
Want wat bedoel je met 1x^x^(-1/2)?
En je schrijft ook nergens op waar je de differentiatie stap doet.
Je kanschrijven als
En dan kom je er denk ik zelf wel uit.
Je maakt gewoon gebruik vanquote:
[..]
Is dat omdat je die x kan wegstrepen?
√x / xquote:
[..]
Misschien doe je hetzelfde, maar je beschrijving is totaal onduidelijk.
Hetzelfde hier
[..]
Dit moet je veel duidelijker beschrijven, dan maak je ook minder fouten.
Want wat bedoel je met 1x^x^(-1/2)?
En je schrijft ook nergens op waar je de differentiatie stap doet.
Je kan
En dan kom je er denk ik zelf wel uit.
Ik deed:
1x ^x ^(-1/2) , formule anders opschrijven
--->
1x^(-1/2)x^(-3/2) de standaardregel toepassen dmv n-1 etc.
= ---> -1/2 ^(-5/2)x^(-3/2) weer de standaardregel toepassen met n-1
Wegstrepen is altijd fout, want het is een term die verraadt dat de gebruiker niet werkelijk begrijpt wat hij of zij aan het doen is. Teller en noemer van een breuk door eenzelfde getal (ongelijk aan nul) delen mag wel.quote:
[..]
Is dat omdat je die x kan wegstrepen?
Wat bedoel je daar mee?quote:
Ik snap niet hoe het x^1/2 x^-1 wordt? Ik zou namelijk denken aan
1x^x^(-1/2)
Oh en 1x = x, die 1 hoef je niet op te schrijven.
Juist die formule. Die 1 zet ik er express neer voor de vermenigvuldiging, dat ik het niet vergeet.quote:
[..]
Wat bedoel je daar mee?
[tex]1x^{x^{-\frac{1}{2}}}[/tex]
Oh en 1x = x, die 1 hoef je niet op te schrijven.
Nogmaals, wat is x^x^(-1/2)?quote:
[..]
Nou die x in de noemer wordt gewoon 1x ofwel x, maar ivm met de deling wordt het x^x^(-1/2)
Snap je al dat hier niks van klopt? Want ik denk dat je daardoor nu rare dingen doet.quote:
[..]
5 / x^5
dit doe je toch als volgt:
die x^5 is hetzelfde als 5x en dan wordt het 5/ 5x en dan
5x^-5 en dus -25x^-6?
Schrijf nu eens in duidelijke stappen op wat je aan het doen bent, want ik snap er geen kloten van.quote:
[..]
Dat is gewoonmaar dan anders opgeschreven.
x wordten dan nog die x uit de noemer wordt
quote:
[..]
Schrijf nu eens in duidelijke stappen op wat je aan het doen bent, want ik snap er geen kloten van.
die √x wordt
dus dan wordt het
Net als je 1/x hebt. met die x doe je niks, met die 1 wel --> x^-1 --> Dit deed ik dus bij het bovenstaande.
Denk eens aan die arme docenten die straks zijn 'werk' moeten nakijken en een puntentelling moeten opstellen. Zelfs het meest uitgekookte antwoordmodel is hier niet tegen opgewassen.quote:
[..]
Schrijf nu eens in duidelijke stappen op wat je aan het doen bent, want ik snap er geen kloten van.
[ Bericht 0% gewijzigd door Riparius op 10-05-2014 14:06:57 ]
Waar komt die -1 vandaan?quote:
moet dat niet -(1/2) zijn i.v.m. de bovenstaande wortel in de teller.
Ik doe gewoon mijn best. Je hoeft mij niet belachelijk lopen te makenquote:
[..]
Denk eens aan die arme docenten die straks zijn 'werk' moeten nakijken en een puntentelling moeten opstellen. Zelf het meest uitgekookte antwoordmodel is hier niet tegen opgewassen.
Nee, delen door x is hetzelfde als vermenigvuldigen met 1/x = x−1.quote:
[..]
Waar komt die -1 vandaan?
moet dat niet -(1/2) zijn i.v.m. de bovenstaande wortel in de teller.
Ik heb het al begrepen dank..
Dan heb je weer zo'n kutte...:
1 / x 3√x
Met die 3 bedoel ik derdemachtswortel..
Ik ging allereerst met de noemer aan de slag:
x 3√x = x^1 * x^(1/3)
Dus 1 / x 3√x = 1 / x^(4/3) en dan loop ik vast..
Dan heb je weer zo'n kutte...:
1 / x 3√x
Met die 3 bedoel ik derdemachtswortel..
Ik ging allereerst met de noemer aan de slag:
x 3√x = x^1 * x^(1/3)
Dus 1 / x 3√x = 1 / x^(4/3) en dan loop ik vast..
Wat doe je hier? Wat bedoel je met wordt?quote:
Ok dat mag.quote:, met de x uit de noemer doe je sowieso al niks... die laat je gewoon x
Dus waarom?quote:dus dan wordt het
Je doet wel wat met die x, met de 1 doe je niks.quote:Net als je 1/x hebt. met die x doe je niks, met die 1 wel --> x^-1 --> Dit deed ik dus bij het bovenstaande.
