SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Ik moet de volgende vergelijking tweemaal impliciet differentiëren (dy/dx, d2y/dx2), maar loop compleet vast.
Gegeven vergelijking:
(1)
Impliciet differentiëren:
(2)
(3)
Y vrijmaken uit de gegeven vergelijking:
(4)
Y invullen:
(5)
Vervolgens kwam ik op het volgende:
(6)
Volgensmij ben ik hier de mist in gegaan, ik denk dat deze stap niet klopt:
(2)
(7)
Iemand die me op weg kan helpen/kan zeggen wat ik fout doe? Net begonnen met impliciet differentiëren, vaak lukt het de eerste keer wel maar gaat het vervolgens mis, hier bijvoorbeeld ook.
Gegeven vergelijking:
(1)
Impliciet differentiëren:
(2)
(3)
Y vrijmaken uit de gegeven vergelijking:
(4)
Y invullen:
(5)
Vervolgens kwam ik op het volgende:
(6)
Volgensmij ben ik hier de mist in gegaan, ik denk dat deze stap niet klopt:
(2)
(7)
Iemand die me op weg kan helpen/kan zeggen wat ik fout doe? Net begonnen met impliciet differentiëren, vaak lukt het de eerste keer wel maar gaat het vervolgens mis, hier bijvoorbeeld ook.


Dat is een beetje overhaast.quote:Op zondag 29 september 2013 21:42 schreef wiskundenoob het volgende:
Stelling van Pythagoras misschien?
Mag je mij vertellen hoe je daaraan komt. Ik heb zo ongeveer alle goniometrische verhoudingen opgesteld wat ik kon bedenken, maar ik kom hier niet bepaald uit. (Twee vergelijkingen - drie onbekenden)quote:Op zondag 29 september 2013 21:57 schreef wiskundenoob het volgende:
[..]
waarom? volgens mij is het antwoord gewoon 2.


nvm klopt nietquote:Op zondag 29 september 2013 21:59 schreef Amoeba het volgende:
[..]
Dat is een beetje overhaast.
[..]
Mag je mij vertellen hoe je daaraan komt. Ik heb zo ongeveer alle goniometrische verhoudingen opgesteld wat ik kon bedenken, maar ik kom hier niet bepaald uit. (Twee vergelijkingen - drie onbekenden)


Is het antwoord 1,5? Volgens mij is het wel 2.quote:Op zondag 29 september 2013 20:47 schreef PizzaGeit het volgende:
Hoi,
Ik heb een vraag. Stel, je hebt een plank, met lengte 2, die schuin vanuit een hoekpunt in een steeg tegen de muur staat. Dan heb je nog een plank, met lengte 3, die schuin vanuit het andere hoekpunt tegen de muur staat. Verder is bekend dat die twee planken elkaar op hoogte 1 snijden, vanaf de grond gezien. Hoe breed is dan de steeg?
Plaatje ter verduidelijking:
[ afbeelding ]
[ Bericht 48% gewijzigd door wiskundenoob op 29-09-2013 22:19:44 ]


Als je bijvoorbeeld weet op welke hoogte een plank tegen een muur aan staat, dan kun je met de stelling van Pythagoras de breedte berekenen. Je kunt het ook berekenen als je van een van de planken weet welke hoek deze maakt met de muur of de grond.quote:Op zondag 29 september 2013 21:57 schreef wiskundenoob het volgende:
[..]
waarom? volgens mij is het antwoord gewoon 2.
Maar deze gegevens zijn niet beschikbaar. Alleen de lengtes van de planken is gegeven, net als de hoogte waarop de planken elkaar kruisen. En dat is onvoldoende om de som op te lossen.


Breedte kan natuurlijk nooit 2 zijn, omdat de schuine zijde van een van de gevormde driehoeken al 2 is; driehoeksongelijkheid.quote:Op zondag 29 september 2013 22:13 schreef wiskundenoob het volgende:
[..]
Is het antwoord 1,5? Volgens mij is het wel 2.
Zin in pizza? Simpel pizzarecept - Uitgebreid pizzarecept! - DIY pizzaschep - Bestron Alfredo Tuning - kookkompas.nl


Ik gooi meteen nog een vraag erachteraan. Stel dat je de volgende vergelijking hebt, waarbij y gedefiniëerd is als een functie van x en je dmv impliciet differentiëren y' moet geven.
(1)
Nu is dit vrij eenvoudig te doen:
(2)
(3)
(4)
Maar stel nu dat er in plaats van g(x) g(x+y) stond, hoe kan je zoiets impliciet differentiëren? Dat is mij namelijk nog niet helemaal duidelijk.
(1)
Nu is dit vrij eenvoudig te doen:
(2)
(3)
(4)
Maar stel nu dat er in plaats van g(x) g(x+y) stond, hoe kan je zoiets impliciet differentiëren? Dat is mij namelijk nog niet helemaal duidelijk.


Kan het 1,25 zijn?quote:Op zondag 29 september 2013 22:24 schreef MaximusTG het volgende:
[..]
Breedte kan natuurlijk nooit 2 zijn, omdat de schuine zijde van een van de gevormde driehoeken al 2 is; driehoeksongelijkheid.


quote:Op zondag 29 september 2013 22:23 schreef lyolyrc het volgende:
[..]
Als je bijvoorbeeld weet op welke hoogte een plank tegen een muur aan staat, dan kun je met de stelling van Pythagoras de breedte berekenen. Je kunt het ook berekenen als je van een van de planken weet welke hoek deze maakt met de muur of de grond.
Maar deze gegevens zijn niet beschikbaar. Alleen de lengtes van de planken is gegeven, net als de hoogte waarop de planken elkaar kruisen. En dat is onvoldoende om de som op te lossen.
Kan je het zo wel oplossen? Ik dacht dat de 2 planken maar op 1 manier kunnen kruizen! Daarom dacht ik dat je het wel kon uitrekenen...


Tenzij de plank plat op de grond ligt. Maar in dat geval kunnen de planken nooit op hoogte 1 snijden.quote:Op zondag 29 september 2013 22:24 schreef MaximusTG het volgende:
[..]
Breedte kan natuurlijk nooit 2 zijn, omdat de schuine zijde van een van de gevormde driehoeken al 2 is; driehoeksongelijkheid.
Volgens mij is het wel mogelijk om dit op te lossen trouwens.
Als je nu eens uitwerkingen post in plaats van lukraak dingen te gaan roepen waar niemand wat mee kan. En heldere uitwerkingen, want vaak zijn je posts maar vaag.quote:


Kijk een post boven jequote:Op zondag 29 september 2013 22:40 schreef Amoeba het volgende:
[..]
Tenzij de plank plat op de grond ligt. Maar in dat geval kunnen de planken nooit op hoogte 1 snijden.
Volgens mij is het wel mogelijk om dit op te lossen trouwens.
[..]
Als je nu eens uitwerkingen post in plaats van lukraak dingen te gaan roepen waar niemand wat mee kan. En heldere uitwerkingen, want vaak zijn je posts maar vaag.


quote:Op zondag 29 september 2013 22:40 schreef wiskundenoob het volgende:
[..]
[ afbeelding ]
Kan je het zo wel oplossen? Ik dacht dat de 2 planken maar op 1 manier kunnen kruizen! Daarom dacht ik dat je het wel kon uitrekenen...
Mag jij mij vertellen hoe je aan die wortel 2 komt.quote:


Stel de eerste plank zit op hoogte a tegen de muur en de tweede plank op hoogte b. En stel de planken snijden op afstand x van de ene muur en op afstand y van de andere muur. Laten we de breedte z noemen (dus z = x+y).
Dan geldt a : z = 1 : y, en b : z = 1 : x. Ofwel ay = z, en bx = z.
Voorts geldt a2 = 4-z2, en b2=9-z2.
Kwadrateren en invullen geeft
(4-z2)y2 = z2, en (9-z2)x2 = z2.
Dit geeft ook weer
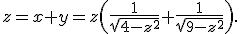
Hieruit volgt
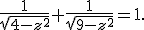
Dit kun je met wat kwadrateren nog wel oplossen.
Dan geldt a : z = 1 : y, en b : z = 1 : x. Ofwel ay = z, en bx = z.
Voorts geldt a2 = 4-z2, en b2=9-z2.
Kwadrateren en invullen geeft
(4-z2)y2 = z2, en (9-z2)x2 = z2.
Dit geeft ook weer
Hieruit volgt
Dit kun je met wat kwadrateren nog wel oplossen.


Ik kwam steeds op onzinnige zooi uit. Ik probeerde jouw x en y uit te drukken in a en b zodat ik 2 vergelijkingen met 2 onbekenden zou krijgen. Ik deed het juist met goniometrische gelijkheden door gelijkvormige driehoeken te gebruiken.quote:Op zondag 29 september 2013 22:47 schreef thabit het volgende:
Stel de eerste plank zit op hoogte a tegen de muur en de tweede plank op hoogte b. En stel de planken snijden op afstand x van de ene muur en op afstand y van de andere muur. Laten we de breedte z noemen (dus z = x+y).
Dan geldt a : z = 1 : y, en b : z = 1 : x. Ofwel ay = z, en bx = z.
Voorts geldt a2 = 4-z2, en b2=9-z2.
Kwadrateren en invullen geeft
(4-z2)y2 = z2, en (9-z2)x2 = z2.
Dit geeft ook weer
Hieruit volgt
Dit kun je met wat kwadrateren nog wel oplossen.
[ Bericht 3% gewijzigd door #ANONIEM op 29-09-2013 22:53:42 ]


Je wil hier een functie van de gedaantequote:Op zondag 29 september 2013 18:10 schreef wiskundenoob het volgende:
Ik kom niet uit bij deze:
3x 2 +2x - 1
9x 2 +6x - 3
(3x +1)2 - 4
(-1/3,-4)
Of nogmaals delen door 3:
(3x +1 )2-4
(1x + 1/3) 2 - 4/3
(-1/3, -4/3)
f(x) = ax2 + bx + c
omwerken tot een vorm waaruit je de coördinaten kunt aflezen van de top van de parabool die de grafiek is van deze functie. Om dit te kunnen doen haal je eerst een geschikte factor buiten haakjes, vervolgens pas je kwadraatafsplitsing toe op de uitdrukking binnen de haakjes, en tenslotte werk je de buitenste haakjes weer weg.
Even een voorbeeld.
f(x) = 3x2 + 2x − 1
Hier kunnen we 3x2 omvormen tot het kwadraat van 3x door met 3 te vermenigvuldigen, maar dan moeten we daarvoor compenseren door weer met 1/3 te vermenigvuldigen, en krijgen we dus
f(x) = ⅓(9x2 + 6x − 3)
f(x) = ⅓((3x + 1)2 − 1 − 3)
f(x) = ⅓((3x + 1)2 − 4)
f(x) = ⅓(3x + 1)2 − 4/3
De functie neemt dus voor x = −⅓ een minimum f(−⅓) = −4/3 aan. De grafiek van de functie is dus een dalparabool met als top het punt met de coördinaten (−⅓; −4/3).
Andere manier: we halen de coëfficiënt 3 van de kwadratische term buiten haakjes, dan krijgen we
f(x) = 3(x2 + ⅔x − ⅓)
f(x) = 3((x + ⅓)2 − 1/9 − ⅓)
f(x) = 3((x + ⅓)2 − 4/9)
f(x) = 3(x + ⅓)2 − 4/3
En weer kunnen we concluderen dat de functie voor x = −⅓ een minimum f(−⅓) = −4/3 bereikt.
De algemene gedaante van een kwadratische functie is
f(x) = ax2 + bx + c, a ≠ 0
Je kunt dit ook met kwadraatafsplitsing omwerken, en daarbij heb je weer de mogelijkheid om bijvoorbeeld eerst met 4a te vermenigvuldigen (methode van Sridhara), maar dan moet je ter compensatie ook weer met een factor 1/4a vermenigvuldigen. Uiteindelijk krijg je dan
f(x) = (1/4a)·(2ax + b)2 − D/4a
waarbij D = b2 − 4ac de discriminant is van de kwadratische veelterm. Deze functie neemt dus voor x = −b/2a een extreme waarde f(−b/2a) = −D/4a aan. Deze extreme waarde is een minimum indien a > 0 en een maximum indien a < 0.
Andere manier: eerst de factor a buiten haakjes halen. Uiteindelijk krijg je dan
f(x) = a(x + b/2a)2 − D/4a
en uiteraard vind je dan ook dat de functie voor x = −b/2a een extreme waarde f(−b/2a) = −D/4a aanneemt. De parabool die de grafiek is van deze functie heeft dus als top het punt met coördinaten
(−b/2a; −D/4a)
In het algemeen is het eenvoudiger om eerst de discriminant van je kwadratische veelterm uit te rekenen, want dan kun je ook meteen de coördinaten van de top van de parabool opschrijven.
Voorbeeld: voor f(x) = 3x2 + 2x − 1 heb je a = 3, b = 2, c = −1, dus D = b2 − 4ac = 4 − 4·3·(−1) = 4 + 12 = 16. De x-coördinaat van de top (xt; yt) van de parabool is dus xt = −b/2a = −2/6 = −1/3 en de y-coördinaat van de top is yt = −D/4a = −16/12 = −4/3. Aangezien a > 0 is de grafiek een dalparabool en aangezien D > 0 zijn er twee snijpunten met de x-as. De x-coördinaten van de snijpunten met de x-as zijn x1 = (−b − √D)/2a = (−2 − 4)/6 = −1 en x2 = (−b + √D)/2a = (−2 + 4)/6 = 1/3.
[ Bericht 0% gewijzigd door Riparius op 01-10-2013 01:21:26 ]


Dit is een klassieker. Iedereen die geïnteresseerd is in dit probleem kan ik aanraden eens te googelen naar crossed ladder problem. Je komt uiteindelijk uit op een vierdegraadsvergelijking (die uiteraard oplosbaar is). Ook via JSTOR zijn er artikelen over te vinden.quote:Op zondag 29 september 2013 22:47 schreef thabit het volgende:
Stel de eerste plank zit op hoogte a tegen de muur en de tweede plank op hoogte b. En stel de planken snijden op afstand x van de ene muur en op afstand y van de andere muur. Laten we de breedte z noemen (dus z = x+y).
Dan geldt a : z = 1 : y, en b : z = 1 : x. Ofwel ay = z, en bx = z.
Voorts geldt a2 = 4-z2, en b2=9-z2.
Kwadrateren en invullen geeft
(4-z2)y2 = z2, en (9-z2)x2 = z2.
Dit geeft ook weer
Hieruit volgt
Dit kun je met wat kwadrateren nog wel oplossen.


Dat is een veel voorkomende reactie van mensen die het probleem voor het eerst onder ogen krijgen. Maar wat je zegt is niet juist, het vraagstuk is op te lossen.quote:Op zondag 29 september 2013 22:23 schreef lyolyrc het volgende:
[..]
Maar deze gegevens zijn niet beschikbaar. Alleen de lengtes van de planken is gegeven, net als de hoogte waarop de planken elkaar kruisen. En dat is onvoldoende om de som op te lossen.


Uiteindelijk heb ik twee vergelijkingen in a en b staan (met een direct verband tussen x+y=z uiteraard), maar dat ging WolframAlpha wat te ver. Ik had met de sinus van dat stuk v/d schuine zijde en de stelling van Pythagoras x en y uitgedrukt in c en d om zo twee vergelijkingen in c en d te krijgen. Maar zelfs Mathematica gaf daar geen output over.quote:Op zondag 29 september 2013 23:17 schreef Riparius het volgende:
[..]
Dat is een veel voorkomende reactie van mensen die het probleem voor het eerst onder ogen krijgen. Maar wat je zegt is niet juist, het vraagstuk is op te lossen.


Ik heb de voorzet van thabit inmiddels gezien en ik moet inderdaad toegeven dat dit op te lossen moet zijn.quote:Op zondag 29 september 2013 23:17 schreef Riparius het volgende:
de hoogte waarop de planken elkaar kruisen. En dat is onvoldoende om de som op te lossen.
Dat is een veel voorkomende reactie van mensen die het probleem voor het eerst onder ogen krijgen. Maar wat je zegt is niet juist, het vraagstuk is op te lossen.


Ik had uiteindelijk:
Overigens zijn d,c de hoogte van mijn ladders tegen de muur.
En uiteraard geldt ook d2 - c2 = 5
Substitueer de gevonden waarde voor d2 in bovenstaande vergelijking, gebruik dat de lengte van het steegje z gegeven wordt door:
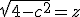
En je bent klaar. Alleen het berekenen van c is een aardige kluif.
Maar dan schieten mijn algebraïsche technieken toch echt te kort. WolframAlpha zegt trouwens dat het ongeveer 1.23122 is. En dat stemt overeen met de vergelijking van Thabit.
[ Bericht 19% gewijzigd door #ANONIEM op 30-09-2013 00:08:28 ]
Overigens zijn d,c de hoogte van mijn ladders tegen de muur.
En uiteraard geldt ook d2 - c2 = 5
Substitueer de gevonden waarde voor d2 in bovenstaande vergelijking, gebruik dat de lengte van het steegje z gegeven wordt door:
En je bent klaar. Alleen het berekenen van c is een aardige kluif.
Maar dan schieten mijn algebraïsche technieken toch echt te kort. WolframAlpha zegt trouwens dat het ongeveer 1.23122 is. En dat stemt overeen met de vergelijking van Thabit.
[ Bericht 19% gewijzigd door #ANONIEM op 30-09-2013 00:08:28 ]


Ga uit van de vergelijking in z van Thabit en substitueer daar z2 = w en werk daarna de wortels weg door (tweemaal!) te kwadrateren. Dan kom je uit op een vierdegraadsvergelijking in w.quote:Op maandag 30 september 2013 00:02 schreef Amoeba het volgende:
Ik had uiteindelijk:
[ afbeelding ]
En uiteraard geldt ook d^2 - c^2 = 5
Maar dan schieten mijn algebraïsche technieken toch echt te kort. WolframAlpha zegt trouwens dat het ongeveer 1.23122 is. En dat stemt overeen met de vergelijking van Thabit.


Je moet volgens mij gewoon (3) nog een keer differentiëren en vervolgens de y' die je in die vergelijking nog 'over' hebt vervangen door je definitie die je hiervoor hebt gevonden (4) of (5). Correct me if I'm wrong.quote:Op zondag 29 september 2013 21:57 schreef jordyqwerty het volgende:
Ik moet de volgende vergelijking tweemaal impliciet differentiëren (dy/dx, d2y/dx2), maar loop compleet vast.
Gegeven vergelijking:
[ afbeelding ] (1)
Impliciet differentiëren:
[ afbeelding ] (2)
[ afbeelding ] (3)
Y vrijmaken uit de gegeven vergelijking:
[ afbeelding ] (4)
Y invullen:
[ afbeelding ] (5)
Vervolgens kwam ik op het volgende:
[ afbeelding ] (6)
Volgensmij ben ik hier de mist in gegaan, ik denk dat deze stap niet klopt:
[ afbeelding ] (2)
[ afbeelding ] (7)
Iemand die me op weg kan helpen/kan zeggen wat ik fout doe? Net begonnen met impliciet differentiëren, vaak lukt het de eerste keer wel maar gaat het vervolgens mis, hier bijvoorbeeld ook.


Ga er straks na mijn college nog eens naar kijken, vandaag wordt immers sowieso weer een wiskunde-dag.quote:Op maandag 30 september 2013 11:20 schreef ulq het volgende:
[..]
Je moet volgens mij gewoon (3) nog een keer differentiëren en vervolgens de y' die je in die vergelijking nog 'over' hebt vervangen door je definitie die je hiervoor hebt gevonden (4) of (5). Correct me if I'm wrong.


Ok post maar of de juiste uitkomst overeenkomt met mijn methode, ben wel benieuwd en ik moet het immers ook onder de knie krijgenquote:Op maandag 30 september 2013 11:42 schreef jordyqwerty het volgende:
[..]
Ga er straks na mijn college nog eens naar kijken, vandaag wordt immers sowieso weer een wiskunde-dag.


(5) volgt direct uit (4) en bij (7) heeft hij de productregel incorrect gebruikt. Impliciet differentiëren is hier feitelijk overbodig.quote:Op maandag 30 september 2013 11:20 schreef ulq het volgende:
[..]
Je moet volgens mij gewoon (3) nog een keer differentiëren en vervolgens de y' die je in die vergelijking nog 'over' hebt vervangen door je definitie die je hiervoor hebt gevonden (4) of (5). Correct me if I'm wrong.


Oh ja klopt, ik bedoelde inderdaad dat ie gewoon (5) moet gebruiken om de y' weg te werken. Maar het enige wat je nog moet doen om het antwoord (de tweede afgeleide van deze functie) te krijgen is (3) nog een keer differentiëren en dan dmv (5) de y' weg werken toch?quote:Op maandag 30 september 2013 12:28 schreef Riparius het volgende:
[..]
(5) volgt direct uit (4) en bij (7) heeft hij de productregel incorrect gebruikt. Impliciet differentiëren is hier feitelijk overbodig.


Nog eenvoudiger: je kunt (5) differentiëren om direct y'' te krijgen.quote:Op maandag 30 september 2013 12:32 schreef ulq het volgende:
[..]
Oh ja klopt, ik bedoelde inderdaad dat ie gewoon (5) moet gebruiken om de y' weg te werken. Maar het enige wat je nog moet doen om het antwoord (de tweede afgeleide van deze functie) te krijgen is (3) nog een keer differentiëren en dan dmv (5) de y' weg werken toch?


Ik weet natuurlijk niet wat je allemaal in Mathematica hebt gestopt, maar een goniometrische oplossing is ook heel goed mogelijk, WolframAlpha heeft daar geen moeite mee, en Mathematica naar ik aanneem dus ook niet.quote:Op zondag 29 september 2013 23:27 schreef Amoeba het volgende:
[..]
Uiteindelijk heb ik twee vergelijkingen in a en b staan (met een direct verband tussen x+y=z uiteraard), maar dat ging WolframAlpha wat te ver. Ik had met de sinus van dat stuk v/d schuine zijde en de stelling van Pythagoras x en y uitgedrukt in c en d om zo twee vergelijkingen in c en d te krijgen. Maar zelfs Mathematica gaf daar geen output over.
Laat ik even uitgaan van de aanduidingen van Thabit hierboven. De kortste van de twee ladders steunt op een hoogte a boven de grond tegen de linker muur en de langste van de twee ladders steunt op een hoogte b boven de grond tegen de rechter muur. Verder noem ik de hoek die de kortste van de twee ladders met de straat maakt α en de hoek die de langste van de twee ladders met de straat maakt β. We hadden we al gezien dat geldt
(1) 1/a + 1/b = 1
Verder hebben we nu
(2) cos α = z/2, cos β = z/3, cot α = z/a, cot β = z/b
zodat
(3) z = cot α + cot β, z = 2·cos α, z = 3·cos β
Zo krijgen we dus voor α en β de voorwaarde
(4) cot α + cot β = 2·cos α = 3·cos β
waarbij moet gelden
(6) 0 < α < π/2, 0 < β < π/2
Dit stelsel kun je numeriek oplossen en dan krijgen we
(7) α ≈ 0,907658, β ≈ 1,14791
En dus hebben we
(8) z = 2·cos α ≈ 1,231186
Algebraïsch gaat het ook prima als je a en b oplost uit het stelsel
(9) b2 − a2 = 5, 1/a + 1/b = 1
Dit levert een vergelijking op die wat makkelijker te hanteren is dan de vergelijking die je voor z af kunt leiden. Aangezien a en b positief zijn volgt uit 1/a + 1/b = 1 dat 1/a < 1 en dus a > 1 en verder is a < 2 aangezien a2 = 4 − z2, zodat we dus voor a een waarde zoeken op het interval (1,2). Numeriek oplossen geeft dan
(10) a ≈ 1,57613, b ≈ 2,73572
De exacte uitdrukkingen zien er inderdaad tamelijk hopeloos uit, maar dat komt omdat de kubische resolventes van de vierdemachtsvergelijkingen die dit stelsel oplevert niet prettig zijn (lees: geen rationale oplossingen hebben). Ik neem aan dat je er begrip voor hebt dat ik die exacte oplossing hier dan ook niet uit ga werken.
Uit 1/a + 1/b = 1 volgt b = a/(a − 1) en substitutie daarvan in b2 − a2 = 5 geeft dan
(11) (a/(a − 1))2 − a2 = 5
en dit kunnen we verder herleiden tot
(12) a4 − 2a3 + 5a2 − 10a + 5 = 0
Numeriek zou je (ook met pen en papier) de gezochte oplossing op het interval (1,2) kunnen benaderen met een Newton-Raphson iteratie, waarbij het voor de hand ligt om als startwaarde a0 = 1,5 te nemen. Dan krijg je dit en dan zie je dat we na enkele iteraties inderdaad op a ≈ 1,57613 uitkomen.
Tot slot zal ik toch nog even aangeven hoe (12) althans in principe exact is op te lossen met de methode van Ferrari. We brengen eerst de termen met de tweede en lagere machten van de onbekende over naar het rechterlid, dit geeft
(13) a4 − 2a3 = −5a2 + 10a − 5
Nu kwadraat afsplitsen in het linkerlid
(14) (a2 − a)2 − a2 = −5a2 + 10a − 5
en de kwadratische term weer overbrengen naar het rechterlid
(15) (a2 − a)2 = −4a2 + 10a − 5
Nu zou het mooi zijn als we het rechterlid ook als een kwadraat konden schrijven, maar dat is hier niet zo, de discriminant van de kwadratische veelterm in het rechterlid is namelijk niet nul. Daarom gaan we een parameter t invoeren waarmee we een beetje kunnen schuiven, zodat we alsnog het rechterlid ook als een kwadraat kunnen schrijven. Maar dan moeten we wel zorgen dat we het linkerlid tevens als een kwadraat kunnen blijven schrijven. Daarom tellen we nu bij beide leden
(16) t(a2 − a) + ¼t2 = ta2 − ta + ¼t2
op, zodat we krijgen
(17) (a2 − a)2 + t(a2 − a) + ¼t2 = −4a2 + 10a − 5 + ta2 − ta + ¼t2
en dit geeft
(18) (a2 − a + ½t)2 = (t − 4)a2 + (10 − t)a + (¼t2 − 5)
Nu willen we t zó kiezen dat de discriminant van de kwadratische veelterm in a in het rechterlid gelijk wordt aan nul, en dus moet gelden
(19) (10 − t)2 − 4(t − 4)(¼t2 − 5) = 0
Uitwerken hiervan geeft
(20) t3 − 5t2 − 20 = 0
En zie, we hebben nu een kubische vergelijking in t, en als we een oplossing hiervan substitueren in (18) dan kunnen we het rechterlid van (18) ook als een kwadraat schrijven, en dan is (18) te herleiden tot twee vierkantsvergelijkingen in a, die we op de bekende manier(en) kunnen oplossen.
Nu heeft (20) echter geen rationale wortels, en dus krijg je hier vrij ongelukkige uitdrukkingen voor t en dus ook voor de waarden van a die je dan krijgt door vervolgens (18) op te lossen. Maar je kunt wel zien dat WolframAlpha het op een soortgelijke manier doet, want als je (20) laat oplossen en je kijkt dan naar de exacte uitdrukkingen voor de oplossingen van (20) dan herken je hier inderdaad precies dezelfde derdemachtswortels als in de exacte uitdrukkingen voor de oplossingen van (12).
[ Bericht 5% gewijzigd door Riparius op 01-10-2013 10:54:41 ]


quote:Op maandag 30 september 2013 12:35 schreef Riparius het volgende:
[..]
Nog eenvoudiger: je kunt (5) differentiëren om direct y'' te krijgen.


Ah, super, bedankt!quote:Op zondag 29 september 2013 22:47 schreef thabit het volgende:
Stel de eerste plank zit op hoogte a tegen de muur en de tweede plank op hoogte b. En stel de planken snijden op afstand x van de ene muur en op afstand y van de andere muur. Laten we de breedte z noemen (dus z = x+y).
Dan geldt a : z = 1 : y, en b : z = 1 : x. Ofwel ay = z, en bx = z.
Voorts geldt a2 = 4-z2, en b2=9-z2.
Kwadrateren en invullen geeft
(4-z2)y2 = z2, en (9-z2)x2 = z2.
Dit geeft ook weer
Hieruit volgt
Dit kun je met wat kwadrateren nog wel oplossen.
Zat een flinke tijd te puzzelen, maar eigenlijk is het best logisch


100-(2x+1)^5 = 68
-(2x+1)^5 = 68-100 ;logische stap toch?
-(2x+1)^5 = -32 ;moet ook nog te volgen zijn?
(2x+1)^5 = 32 ;alle beide kanten maal -1
2x+1 = 5_sqrt(32) = 2 ;5de macht links, verdwijnt door links en rechts 5de machtswortel te nemen, 5demachtswortel van 32 is 2, want 2^5 = 32
2x+1 = 2 ;logisch
2x = 1 ;gewoon links en rechts 1 eraf
x = 1/2 ;beide kanten door 2 delen
[ Bericht 22% gewijzigd door MaximusTG op 30-09-2013 18:04:58 ]
-(2x+1)^5 = 68-100 ;logische stap toch?
-(2x+1)^5 = -32 ;moet ook nog te volgen zijn?
(2x+1)^5 = 32 ;alle beide kanten maal -1
2x+1 = 5_sqrt(32) = 2 ;5de macht links, verdwijnt door links en rechts 5de machtswortel te nemen, 5demachtswortel van 32 is 2, want 2^5 = 32
2x+1 = 2 ;logisch
2x = 1 ;gewoon links en rechts 1 eraf
x = 1/2 ;beide kanten door 2 delen
[ Bericht 22% gewijzigd door MaximusTG op 30-09-2013 18:04:58 ]
Zin in pizza? Simpel pizzarecept - Uitgebreid pizzarecept! - DIY pizzaschep - Bestron Alfredo Tuning - kookkompas.nl


Zit even mobiel. Maar vijfde machts wortel uit 32; dat is 32^(1/5). Enig idee hoe je dit uitrekent?
kloep kloep


Priemgetallen van maken.quote:Op maandag 30 september 2013 18:00 schreef Borizzz het volgende:
Zit even mobiel. Maar vijfde machts wortel uit 32; dat is 32^(1/5). Enig idee hoe je dit uitrekent?


Ah, zo dus, helemaal niet zo moeilijk eigenlijk. Gewoon 5e machtswortel nemen van beide kanten.quote:Op maandag 30 september 2013 17:59 schreef MaximusTG het volgende:
100-(2x+1)^5 = 68
-(2x+1)^5 = 68-100 ;logische stap toch?
-(2x+1)^5 = -32 ;moet ook nog te volgen zijn?
(2x+1)^5 = 32 ;alle beide kanten maal -1
2x+1 = 5_sqrt(32) = 2 ;5de macht links, verdwijnt door links en rechts 5de machtswortel te nemen, 5demachtswortel van 32 is 2, want 2^5 = 32
2x+1 = 2 ;logisch
2x = 1 ;gewoon links en rechts 1 eraf
x = 1/2 ;beide kanten door 2 delen
Ik meen het, als ik niet in het antwoordenboekje keek voor een antwoord had ik gewoon serieus 5 keer achter elkaar (2x+1) geschreven lol.
Gelukkig is er ook een andere route.
Dankjewel
Learn how to eat in the jungle full of hyenas


Ik kan je nog 4 andere antwoorden geven, mocht dat nodig zijn.quote:Op maandag 30 september 2013 18:18 schreef Spinosaurus het volgende:
[..]
Ah, zo dus, helemaal niet zo moeilijk eigenlijk. Gewoon 5e machtswortel nemen van beide kanten.
Ik meen het, als ik niet in het antwoordenboekje keek voor een antwoord had ik gewoon serieus 5 keer achter elkaar (2x+1) geschreven lol.
Gelukkig is er ook een andere route.
Dankjewel


Er is maar één antwoord toch? Je bedoelt 4 andere manieren?quote:Op maandag 30 september 2013 22:33 schreef Amoeba het volgende:
[..]
Ik kan je nog 4 andere antwoorden geven, mocht dat nodig zijn.
Learn how to eat in the jungle full of hyenas


Ik moet een kwadratische vergelijking bepalen(ax 2 +bx +c) met de volgende gegevens:
Top: (0,0) en gaat ook door punt: (1,2).
Hoe pak ik dit aan?
Enige wat ik kan bedenken: er is geen constante. Dus dan krijg je f(x) = (h)2 en h is 2 1/2
Of zoals bij lin. vergl. y/x = 2/1 = hellingsgetal dus y = x 2 +2x +0
Top is volgens mij ook gelijke het enige nulpunt.
[ Bericht 5% gewijzigd door wiskundenoob op 30-09-2013 22:54:57 ]
Top: (0,0) en gaat ook door punt: (1,2).
Hoe pak ik dit aan?
Enige wat ik kan bedenken: er is geen constante. Dus dan krijg je f(x) = (h)2 en h is 2 1/2
Of zoals bij lin. vergl. y/x = 2/1 = hellingsgetal dus y = x 2 +2x +0
Top is volgens mij ook gelijke het enige nulpunt.
[ Bericht 5% gewijzigd door wiskundenoob op 30-09-2013 22:54:57 ]


Ik hoopte al dat je nieuwsgierig zou worden. Algemeen geldt dat een polynoom van de graad n ook n nulpunten heeft, als je de multipliciteit van ieder nulpunt meeneemtquote:Op maandag 30 september 2013 22:34 schreef Spinosaurus het volgende:
[..]
Er is maar één antwoord toch? Je bedoelt 4 andere manieren?
Dus er zijn 5 oplossingen, maar daarvoor heb je wel complexe getallen nodig.


Dat is juist, c = 0.quote:Op maandag 30 september 2013 22:39 schreef wiskundenoob het volgende:
Ik moet een kwadratische vergelijking bepalen(ax 2 +bx +c) met de volgende gegevens:
Top: (0,0) en gaat ook door punt: (1,2).
Hoe pak ik dit aan?
Enige wat ik kan bedenken: er is geen constante. Dus dan krijg je f(x) = (h)2 en h is 2 1/2
Of zoals bij lin. vergl. y/x = 2/1 = hellingsgetal dus y = x 2 +2x +0
Top is volgens mij ook gelijke het enige nulpunt.
Schrijf nu eens y = x(ax+b) en gebruik dat (1,2) een functiewaarde is. Maar je weet ook dat xtop = -b/(2a) = 0
Volgens mij is het dan wel heel eenvoudig om te concluderen wat f(x) nu moet zijn.


a ≠ 0, anders heb je geen polynoom van de tweede graad.quote:Op maandag 30 september 2013 23:02 schreef wiskundenoob het volgende:
b = 0 ? Omdat a niet nul kan zijn?
Maar inderdaad, uit -b/(2a) = 0 concludeer je dat b = 0.
Substitueer nu dat punt in je vergelijking en je vindt op z'n janboerenfluitjes dat a = 2 en dus f(x) = 2x2


Yep
Lang geleden maar volgens mij is het gewoon y=2x^2
Lang geleden maar volgens mij is het gewoon y=2x^2
Winnaar wielerprono 2006 en biatlon wk prono 2016


Overigens voldoet f(x) = x2 + x niet aan beide voorwaarden, want f(x) heeft geen top in de oorsprong.quote:
[ Bericht 2% gewijzigd door #ANONIEM op 30-09-2013 23:14:26 ]


Nee, dat is niet waar
edit: haha, ik dacht even dat ik het verkeerd gelezen had, maar het was wel een edit
edit: haha, ik dacht even dat ik het verkeerd gelezen had, maar het was wel een edit
Zin in pizza? Simpel pizzarecept - Uitgebreid pizzarecept! - DIY pizzaschep - Bestron Alfredo Tuning - kookkompas.nl


afgeleide in (0,0) moest toch ook 0 zijnquote:Op maandag 30 september 2013 23:10 schreef Amoeba het volgende:
[..]
Overigens voldoet f(x) = x2 + x ook niet aan beide voorwaarden, want f(x) heeft geen top in de oorsprong.
Winnaar wielerprono 2006 en biatlon wk prono 2016


