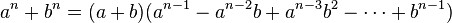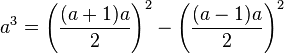[Bèta wiskunde] Huiswerk- en vragentopic

Wow, Riparius, je hebt gelijk: achteraf sla ik mezelf voor mijn kop dat ik het niet zag. Je kan gewoon een soort 'completing the square' gebruiken (ik weet niet helemaal of ik die term correct gebruik, ik dacht dat het de Engelse benoeming is voor technieken als deze):

SPOILER

Om spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.

quote:

Op donderdag 25 juli 2013 00:06 schreef randomo het volgende:

[..]

(Onbegrijpelijk trouwens, hoe mensen op sommige identiteiten komen...)

Er is niets onbegrijpelijks aan, en ik denk dat een beetje HBS'er of gymnasiast hier pakweg een eeuw geleden of zelfs een halve eeuw geleden geen moeite mee zou hebben gehad. Je was zelf al op het idee gekomen om in het merkwaardig product

(a + b)(a² − ab + b²) = a³ + b³

a² in de plaats te stellen van a en b² in de plaats van b, zodat je vond

a⁶ + b⁶ = (a² + b²)(a⁴ − a²b² + b⁴)

Welnu, als je in het merkwaardig product

(a + b)² = a² + 2ab + b²

op dezelfde manier a² in de plaats stelt van a en b² in de plaats van b, dan heb je

a⁴ + 2a²b² + b⁴ = (a² + b²)²

Het linkerlid lijkt nu erg op a⁴ − a²b² + b⁴, nauwkeuriger gezegd, het verschil met a⁴ + 2a²b² + b⁴ bedraagt 3a²b². We hebben dus

a⁴ − a²b² + b⁴ = (a² + b²)² − 3a²b²

Dit is in feite niets anders dan het toepassen van kwadraatafsplitsing: a⁴ + b⁴ = (a² + b²)² − 2a²b². Nu willen we het rechterlid schrijven als een verschil van twee kwadraten, omdat we dan het merkwaardig product a² − b² = (a + b)(a − b) kunnen toepassen. We hebben 3a²b² = (√3·ab)², en dus hebben we

a⁴ − a²b² + b⁴ = (a² + b²)² − (√3·ab)²

en dit geeft

a⁴ − a²b² + b⁴ = ((a² + b²) + √3·ab)((a² + b²) − √3·ab)

oftewel

a⁴ − a²b² + b⁴ = (a² + √3·ab + b²)(a² − √3·ab + b²)

zodat we uiteindelijk krijgen

a⁶ + b⁶ = (a² + b²)(a² + √3·ab + b²)(a² − √3·ab + b²)

Elk van de kwadratische veeltermen in a en b in het rechterlid is irreducibel over R, zoals je gemakkelijk kunt nagaan door de discriminanten van deze veeltermen te berekenen. En uiteraard kun je deze identiteit nu controleren in WolframAlpha.

De kwadratische veeltermen in het rechterlid zijn niet irreducibel over C, dus als je wel complexe coëfficiënten toestaat, dan kun je a⁶ + b⁶ wel schrijven als het product van zes lineaire factoren in a en b, en dan krijg je dit. Deze lineaire factorisatie hangt uiteraard samen met de wortels van de vergelijking z⁶ = −1. Als je a/b = z substitueert, oftewel a = bz, dan heb je a⁶ + b⁶ = b⁶(z⁶ + 1) zodat het ontbinden in lineaire factoren neerkomt op het oplossen in C van de vergelijking z⁶ + 1 = 0. De beeldpunten in het complexe vlak van de oplossingen van deze vergelijking vormen zoals bekend een regelmatige zeshoek waarvan de hoekpunten op de eenheidscirkel liggen.

quote:

Op donderdag 25 juli 2013 01:13 schreef randomo het volgende:
Wow, Riparius, je hebt gelijk: achteraf sla ik mezelf voor mijn kop dat ik het niet zag. Je kan gewoon een soort 'completing the square' gebruiken (ik weet niet helemaal of ik die term correct gebruik, ik dacht dat het de Engelse benoeming is voor technieken als deze):

SPOILER

Om spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.

Inderdaad, dat is het. Je was me net voor omdat ik bezig was het allemaal nog eens netjes uit te leggen in de post hierboven (die natuurlijk ook voor de andere meelezers is bedoeld).

Maar goed, nu nog de vraag hoe je

a⁵ + b⁵

zo ver mogelijk ontbindt in veeltermen in a en b met uitsluitend reële coëfficiënten. Dit is lastiger, maar je kunt dezelfde elementaire technieken gebruiken.

Goed, ook ik lees de Portugese wikipedia eens door.


Dus:

(a+b)(a⁴ -a³b +(ab)² -ab³+b⁴) = a⁵ + b⁵

Dan rest ons het ontbinden van (a⁴ -a³b +(ab)² -ab³+b⁴) in factoren.. Nu buig ik me weer over mijn schrift.

Ook dit zal wel weer niet mogelijk zijn in lineaire veeltermen..

[ Bericht 20% gewijzigd door Amoeba op 25-07-2013 02:08:59 ]

quote:

Op donderdag 25 juli 2013 02:02 schreef Amoeba het volgende:
Goed, ook ik lees de Portugese wikipedia eens door.

[ afbeelding ]
Dus:

(a + b)(a⁴ - a³b + (ab)² - ab³ + b⁴) = a⁵ + b⁵

Dan rest ons het ontbinden van (a⁴ - a³b + (ab)² - ab³ + b⁴) in factoren..

Inderdaad.

quote:

Op donderdag 25 juli 2013 02:09 schreef Riparius het volgende:

[..]

Inderdaad.

Ik zal hier maar even iets nuttigs plaatsen..

Je stelt dat gymnasten hier geen moeite mee zouden hebben, halverwege de vorige eeuw. Nu trek ik mij dat natuurlijk heeeel erg aan zijnde (net geen) gymnast, maar toch heb ik één vraag.

1. De machten van a en b in het antwoord, zijn deze in N, of beter gezegd, is het de bedoeling dat deze in N zijn?

[ Bericht 5% gewijzigd door Amoeba op 25-07-2013 03:12:33 ]

quote:

Op donderdag 25 juli 2013 02:58 schreef Amoeba het volgende:

[..]

Ik zal hier maar even iets nuttigs plaatsen..

Je stelt dat gymnasten hier geen moeite mee zouden hebben, halverwege de vorige eeuw. Nu trek ik mij dat natuurlijk heeeel erg aan zijnde (net geen) gymnast, maar toch heb ik één vraag.

1. De machten van a en b in het antwoord, zijn deze in N, of beter gezegd, is het de bedoeling dat deze in N zijn?

Ja, want het is de bedoeling te ontbinden in veeltermen in a en b. En we spreken alleen van een veelterm of polynoom in één of meer variabelen als de uitdrukking alleen niet-negatieve gehele machten van de variabele(n) bevat en verder alleen is samengesteld uit constanten met gebruikmaking van uitsluitend (een eindig aantal) optellingen, aftrekkingen en vermenigvuldigingen.

quote:

Op donderdag 25 juli 2013 03:33 schreef Riparius het volgende:

[..]

Ja, want het is de bedoeling te ontbinden in veeltermen in a en b. En we spreken alleen van een veelterm of polynoom in één of meer variabelen als de uitdrukking alleen niet-negatieve gehele machten van de variabele(n) bevat en verder alleen is samengesteld uit constanten met gebruikmaking van uitsluitend optelling, aftrekking en vermenigvuldiging.

Weer wat geleerd. Ik zat de hele tijd te prutsen met ((a-b)(a+b))², maar dat lijkt niet de juiste weg.

Als iemand 't praktisch vindt:

a⁵ + b⁵ = (a+b)((a³ - b³)(a-b)+(ab)²)

[ Bericht 28% gewijzigd door Amoeba op 25-07-2013 04:10:00 ]

quote:

Op donderdag 25 juli 2013 01:19 schreef Riparius het volgende:

[..]

Er is niets onbegrijpelijks aan, en ik denk dat een beetje HBS'er of gymnasiast hier pakweg een eeuw geleden of zelfs een halve eeuw geleden geen moeite mee zou hebben gehad.
[...]

Ik dacht al dat je iets dergelijks zou zeggen
Ik realiseer me dat dit stof is die ik me nooit helemaal eigen heb gemaakt, en dat was ook niet nodig: voor wiskunde heb ik zonder moeite prima cijfers gehaald op de middelbare school. Als ik nu wat minder elementaire wiskunde probeer te doen (bijvoorbeeld die Putnam problemen waar ik laatst al wat over gepost heb) loop ik wel vaak tegen dit soort dingen aan.

Ik doelde overigens niet specifiek de identiteiten op die pagina hoewel

toch wel een beetje weergeeft wat ik bedoel. Hoewel ik zelf een lichte aversie heb tegen mensen die bij elke identiteit roepen dat het magie is, heb ik bij sommige identiteiten datzelfde gevoel ook wel een beetje. Ik bedoel maar: ik kan de formule controleren en zo begrijpen dat de formule klopt, maar als ik de opdracht had om een derdemacht te schrijven als het verschil van twee kwadraten, denk ik niet dat ik met die identiteit op de proppen zou kunnen komen.

quote:

Op donderdag 25 juli 2013 02:02 schreef Amoeba het volgende:
[...]
an + bn = (a + b)
[...]

Dit geldt overigens alleen voor oneven n

quote:

Op donderdag 25 juli 2013 11:16 schreef wiskundenoob het volgende:

[..]

Wat doe je precies om tot de 2e stap toe te komen?

x²-y² = (x+y)(x-y)

quote:

Op donderdag 25 juli 2013 00:26 schreef randomo het volgende:
[..]

Die gaat alleen over complexe variabelen, en geeft alleen aan dat zo'n ontbinding bestaat, niet wat deze is (en volgens mij niet eens dat deze uniek is, maar dat weet ik niet helemaal zeker).

Je kunt a^6=-b^6 gewoon opschrijven als (a/b)^6=-1 en dit oplossen. Dan kun je a^6+b^6 opschrijven als het product van al zijn complexe nulpunten, dit kan vanwege de hoofdstelling van de algebra. Je kunt sommige van die factoren met elkaar vermenigvuldigen en dan vind je ook de uitdrukking die je zocht.

Zo kun jij bijvoorbeeld vinden dat:


[ Bericht 8% gewijzigd door Mathemaat op 25-07-2013 15:17:23 ]

quote:

Op donderdag 25 juli 2013 13:19 schreef Mathemaat het volgende:

[..]

Je kunt a^6=-b^6 gewoon opschrijven als (a/b)^6=-1 en dit oplossen. Dan kun je a^6+b^6 opschrijven als het product van al zijn complexe nulpunten, dit kan vanwege de hoofdstelling van de algebra. Je kunt sommige van die factoren met elkaar vermenigvuldigen en dan vind je ook de uitdrukking die je zocht.

Zo kun jij bijvoorbeeld vinden dat:

Nu begrijp ik pas wat je bedoelt, en ja, nu je die ontbinding hebt gevonden kan ik moeilijk meer beweren dat je er niks aan hebt

quote:

Op donderdag 25 juli 2013 13:19 schreef Mathemaat het volgende:

[..]

Je kunt a^6=-b^6 gewoon opschrijven als (a/b)^6=-1 en dit oplossen. Dan kun je a^6+b^6 opschrijven als het product van al zijn complexe nulpunten, dit kan vanwege de hoofdstelling van de algebra. Je kunt sommige van die factoren met elkaar vermenigvuldigen en dan vind je ook de uitdrukking die je zocht.

Zo kun jij bijvoorbeeld vinden dat:

Nice, ik kom bij gebruik maken van de techniek in post #141 uit op ,
wat natuurlijk hetzelfde is.

quote:

Op donderdag 25 juli 2013 22:18 schreef VanishedEntity het volgende:

[..]

Nice, ik kom bij gebruik maken van de techniek in post #141 uit op ,
wat natuurlijk hetzelfde is.

Nee, je maakt een tekenfout. De oplossing van Mathemaat klopt wel. Je zou moeten vinden

quote:

Op donderdag 25 juli 2013 23:42 schreef Riparius het volgende:

[..]

Nee, je maakt een tekenfout. De oplossing van Mathemaat klopt wel. Je zou moeten vinden

Dammit... Foiled by sign swapping again

Anywayz, dan vind ik

persoonlijk eleganter.

quote:

Op donderdag 25 juli 2013 10:53 schreef randomo het volgende:

[..]

Ik dacht al dat je iets dergelijks zou zeggen
Ik realiseer me dat dit stof is die ik me nooit helemaal eigen heb gemaakt, en dat was ook niet nodig: voor wiskunde heb ik zonder moeite prima cijfers gehaald op de middelbare school. Als ik nu wat minder elementaire wiskunde probeer te doen (bijvoorbeeld die Putnam problemen waar ik laatst al wat over gepost heb) loop ik wel vaak tegen dit soort dingen aan.

Die opmerking was natuurlijk niet aan jou persoonlijk gericht. Vroeger werd er op school veel meer aandacht besteed aan het verwerven van goede algebraïsche vaardigheden. Dat kun je goed zien als je oude algebra boekjes bekijkt, bijvoorbeeld op de site van het Nederlands schoolmuseum. Toen was algebra ook een apart schoolvak. Tegenwoordig vindt men die vaardigheden niet meer zo nodig, maar ten onrechte: bij veel vervolgopleidingen heb je het gewoon nodig, en ook als je wat verder wil met wiskunde is het onmisbaar.

quote:

Ik doelde overigens niet specifiek de identiteiten op die pagina hoewel
[ afbeelding ]
toch wel een beetje weergeeft wat ik bedoel. Hoewel ik zelf een lichte aversie heb tegen mensen die bij elke identiteit roepen dat het magie is, heb ik bij sommige identiteiten datzelfde gevoel ook wel een beetje. Ik bedoel maar: ik kan de formule controleren en zo begrijpen dat de formule klopt, maar als ik de opdracht had om een derdemacht te schrijven als het verschil van twee kwadraten, denk ik niet dat ik met die identiteit op de proppen zou kunnen komen.

Het is veel eenvoudiger dan het er op het eerste gezicht uitziet. Dit is een kleine variatie op de oeroude Babylonische truc (zie hier) om een rechthoek te transformeren tot een L-vorm die bestaat uit een vierkant waaraan in één hoek een kleiner vierkant ontbreekt.

Stel we hebben een rechthoekig stuk land met lengte a en breedte b, dan is het gemiddelde van de lengte en de breedte ½(a + b). We kunnen dit gemiddelde uiteraard krijgen door hetzij de helft van het verschil (a − b) van a af te halen, dus ½(a + b) = a − ½(a − b) hetzij de helft van het verschil bij b op te tellen, dus ½(a + b) = b + ½(a − b). Als we dus van de lengte van de rechthoek een strook af halen van b bij ½(a − b) en deze aan de breedte toevoegen, dan hebben we een L-vormige figuur die bestaat uit een vierkant waarvan de zijde gelijk is aan het gemiddelde ½(a + b) en waaraan in één hoekpunt een kleiner vierkant met een zijde gelijk aan het halve verschil ½(a − b) ontbreekt, zodat

ab = (½(a + b))² − (½(a − b))²

Bedenk je dan dat a³ = a·a² en substitueer je b = a², dan heb je

a³ = (½(a + a²))² − (½(a − a²))²

en dat is in wezen dezelfde identiteit.

quote:

[..]

Dit geldt overigens alleen voor oneven n

Inderdaad.

Riparius, nu de oplossing van de opgave bekend is zou ik wel eens willen weten welk merkwaardig product in aanmerking komt om a^4 - a^3b +(ab)^2 - ab^3 + b^4 te ontbinden. Ik heb verleden nacht daar mijn hoofd over gebroken, maar ik zie het niet.

quote:

Op donderdag 25 juli 2013 13:19 schreef Mathemaat het volgende:

[..]

Je kunt a^6=-b^6 gewoon opschrijven als (a/b)^6=-1 en dit oplossen. Dan kun je a^6+b^6 opschrijven als het product van al zijn complexe nulpunten, dit kan vanwege de hoofdstelling van de algebra. Je kunt sommige van die factoren met elkaar vermenigvuldigen en dan vind je ook de uitdrukking die je zocht.

Zo kun jij bijvoorbeeld vinden dat:

En ik begrijp niet helemaal hoe je (a/b)^5 = -1 oplost in C Waar ik overigens het gevoel heb dat ik dit wel zou moeten kunnen.

quote:

Op vrijdag 26 juli 2013 00:25 schreef Amoeba het volgende:
Riparius, nu de oplossing van de opgave bekend is zou ik wel eens willen weten welk merkwaardig product in aanmerking komt om a^4 - a^3b +(ab)^2 - ab^3 + b^4 te ontbinden. Ik heb verleden nacht daar mijn hoofd over gebroken, maar ik zie het niet.

Zoals inmiddels duidelijk is kun je a⁵ + b⁵ ontbinden door a/b = z oftewel a = bz te substitueren, zodat

a⁵ + b⁵ = b⁵(z⁵ + 1).

Dan komt het ontbinden neer op het vinden van de (lineaire) factoren van z⁵ + 1 en dus het oplossen in C van de vergelijking z⁵ + 1 = 0.

Complexe wortels van een algebraïsche vergelijking met reële coëfficiënten treden altijd op als geconjugeerde paren, en omdat som en product van twee geconjugeerde complexe getallen reëel zijn, levert elk paar geconjugeerde wortels van de vergelijking dan een kwadratische factor op met reële coëfficiënten. Immers, als z₁ en z₂ twee toegevoegd complexe wortels zijn van de vergelijking z⁵ + 1 = 0, dan bevat z⁵ + 1 een factor (z − z₁) en een factor (z − z₂) en dus een kwadratische factor (z − z₁)(z − z₂) = z² − (z₁ + z₂)z + z₁z₂ waarvan de coëfficiënten reëel zijn. Maar om deze werkwijze te gebruiken moet je wel iets van complexe getallen weten en moet je ook in staat zijn de vergelijking z⁵ + 1 = 0 algebraïsch op te lossen.

Zoals gezegd is het ook mogelijk a⁴ − a³b + a²b² − ab³ + b⁴ met louter elementaire (school)algebra te ontbinden in veeltermen in a en b met reële coëfficiënten. Dit gaat als volgt.

We beginnen weer met kwadraatafsplitsing, toegepast op de termen met een positief teken. Aangezien (a² + b²)² = a⁴ + 2a²b² + b⁴ hebben we a⁴ + a²b² + b⁴ = (a² + b²)² − a²b² en dus

a⁴ − a³b + a²b² − ab³ + b⁴ = (a² + b²)² − a³b − ab³ − a²b²

Nu is het de bedoeling de uitdrukking in het rechterlid uiteindelijk te herleiden tot een verschil van twee kwadraten. De termen (a² + b²)² en a²b² zijn al kwadraten, dus die laat ik nu even staan. Bij de termen a³b en ab³ kan ik een factor ab buiten haakjes halen zodat binnen haakjes (a² + b²) overblijft. Dan hebben we

a⁴ − a³b + a²b² − ab³ + b⁴ = (a² + b²)² − ab(a² + b²) − a²b²

Nu kunnen we nogmaals kwadraatafsplitsing toepassen op (a² + b²)² − ab(a² + b²). Stel om dit gemakkelijker te zien even a² + b² = p, dan hebben we p² − ab·p = (p −½ab)² − (½ab)², zodat we dus krijgen

a⁴ − a³b + a²b² − ab³ + b⁴ = ((a² + b²) − ½ab)² − (½ab)² − a²b²

en dus

a⁴ − a³b + a²b² − ab³ + b⁴ = (a² − ½ab + b²)² − (5/4)·a²b²

Nu is ook (5/4)·a²b² = (½√5·ab)² zodat we hebben

a⁴ − a³b + a²b² − ab³ + b⁴ = (a² − ½ab + b²)² − (½√5·ab)²

waarmee de uitdrukking is herleid tot een verschil van twee kwadraten. Hiervoor kunnen we nu schrijven

a⁴ − a³b + a²b² − ab³ + b⁴ = ((a² − ½ab + b²) − ½√5·ab)((a² − ½ab + b²) + ½√5·ab)

oftewel

a⁴ − a³b + a²b² − ab³ + b⁴ = (a² − (½ + ½√5)ab + b²)(a² − (½ − ½√5)ab + b²)

QED

[ Bericht 0% gewijzigd door Riparius op 26-07-2013 14:24:20 ]

Wanneer ik heb dat:

z⁵ = -1 = e^{π i}
|z⁵| = 1


Krijg ik voor mijn oplossingen in C:

z = e^{(π/5 + k*2/5π) i}

z = e^{π/5 i}
z = e^{3π/5 i}
z = e^{5π/5 i}
z = e^{7π/5 i}
z = e^{9π/5 i}


z = cos(0) + i sin(0) = 1
z = cos(2π/5) + i sin(2π/5)
z = cos(4π/5) + i sin(4π/5)
z = cos(6π/5) + i sin(6π/5)
z = cos(8π/5) + i sin(8π/5)

Ik ken alleen geen exacte uitdrukkingen hiervoor.

[ Bericht 4% gewijzigd door Amoeba op 26-07-2013 03:02:54 ]

quote:

Op vrijdag 26 juli 2013 00:28 schreef Amoeba het volgende:

[..]

En ik begrijp niet helemaal hoe je (a/b)^5 = -1 oplost in C Waar ik overigens het gevoel heb dat ik dit wel zou moeten kunnen.

Substitutie van a/b = z oftewel a = bz geeft

a⁵ + b⁵ = b⁵(z⁵ + 1)

zodat ontbinden neer komt op het vinden van de (lineaire) factoren van z⁵ + 1 en dus het oplossen in C van de vergelijking

z⁵ + 1 = 0

We zien dat z = −1 een oplossing is van deze vergelijking zodat z⁵ + 1 een factor (z + 1) bevat. Uitvoeren van een polynoomstaardeling levert dan op dat we kunnen schrijven

(z + 1)(z⁴ − z³ + z² − z + 1) = 0

zodat we om de overige vier wortels van de vergelijking z⁵ + 1 = 0 te vinden nog de vierdegraadsvergelijking

z⁴ − z³ + z² − z + 1 = 0

op moeten lossen. Dit kun je op verschillende manieren doen. Om te beginnen kun je hier op een volkomen analoge manier te werk gaan als ik hierboven laat zien voor de ontbinding van a⁴ − a³b + a²b² − ab³ + b⁴. Dan pas je dus tweemaal kwadraatafsplitsing toe om het vierdegraadspolynoom in het linkerlid te herleiden tot een product van twee kwadratische polynomen, waarna je alleen nog twee vierkantsvergelijkingen op hoeft te lossen.

Een andere manier om deze vergelijking op te lossen is middels een geschikt gekozen substitutie. We hebben hier van doen met een zogeheten wederkerige vergelijking van even graad, en deze zijn te herleiden tot een vergelijking waarvan de graad nog slechts de helft van de graad van de oorspronkelijke vergelijking bedraagt. Op de theorie van de wederkerige vergelijkingen ga ik hier niet in, daar heb ik je namelijk al eens een keer iets over uitgelegd. Delen we beide leden door z² (hetgeen is toegestaan aangezien z = 0 geen wortel is van de vergelijking) dan krijgen we

z² - z + 1 − 1/z + 1/z² = 0

waarvoor we kunnen schrijven

(z + 1/z)² − (z + 1/z) − 1 = 0

en substutie w = z + 1/z geeft dan

w² − w − 1 = 0

Dit is een vierkantsvergelijking met als wortels w_1,2 = ½ ± ½√5 zodat je nu alleen nog de vergelijkingen z + 1/z = ½ + ½√5 en z + 1/z = ½ − ½√5 hoeft op te lossen, oftewel we hebben

z² − (½ + ½√5)z + 1 = 0 ∨ z² − (½ − ½√5)z + 1 = 0

Een heel andere manier om de vergelijking z⁵ + 1 = 0 op te lossen is gebruik te maken van de formule van De Moivre

(cos φ + i·sin φ)ⁿ = cos nφ + i·sin nφ

Op grond hiervan is het direct duidelijk dat de vijf wortels van de vergelijking zijn te schrijven als

z_k = cos((2k − 1)π/5) + i·sin((2k − 1)π/5), k = 1..5

en met behulp van de formule van Euler kun je dit ook compacter schrijven als

z_k = e^{i·(2k − 1)π/5}, k = 1..5

Nu zie je dat z₁ = e^i·π/5 en z₅ = e^i·9π/5 = e^−i·π/5 toegevoegd complex zijn, zodat z⁵ + 1 dus een reële kwadratische factor (z − z₁)(z − z₅) = (z − e^i·π/5)(z − e^−i·π/5) = z² − (e^i·π/5 + e^−i·π/5)z + 1 bevat, oftewel een kwadratische factor

z² − 2·cos(π/5)·z + 1

Evenzo zijn z₂ en z₄ toegevoegd complex, en deze leveren een reële kwadratische factor

z² − 2·cos(3π/5)·z + 1

De eerste van deze kwadratische factoren correspondeert met z² − (½ + ½√5)z + 1 en de tweede met z² − (½ − ½√5)z + 1, zodat we hebben

cos(π/5) = ¼ + ¼√5, cos(3π/5) = ¼ − ¼√5

We kunnen dus de ontbinding van a⁵ + b⁵ in veeltermen in a en b met reële coëfficiënten ook als volgt schrijven in goniometrische vorm

a⁵ + b⁵ = (a + b)(a² − 2ab·cos(π/5) + b²)(a² − 2ab·cos(3π/5) + b²)

Het is in het algemeen mogelijk zowel aⁿ − bⁿ als aⁿ + bⁿ voor n > 2 te schrijven in een dergelijke goniometrische vorm als een product van lineaire en kwadratische veeltermen in a en b met reële coëfficiënten, waarbij de kwadratische veeltermen doen denken aan de cosinusregel c² = a² − 2ab·cos γ + b². De overeenstemming met de cosinusregel is niet toevallig maar wordt inzichtelijk door het zogeheten cirkeltheorema van Cotes.

quote:

Op vrijdag 26 juli 2013 04:12 schreef Riparius het volgende:

[..]

SPOILER

Om spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.

De 2 hoofdstukken die ik heb gehad over complexe getallen beschreven inderdaad de formule van de Moive en de formule van Euler, vandaar dat ik die e-machten (met wat moeite) ook had weten te produceren. Daarnaast wat rekenen met complexe getallen i.c.m. de natuurkunde, recursieve formules etc. Ik vind het uitermate storend dat mijn geheugen niet beter in staat is om die technieken wat beter te onthouden dan half.

Het oplossen van een vierdegraadsvergelijking hebben we echter niet behandeld. Het hoofdstuk bleef beperkt tot het oplossen van een gereduceerde kubische vergelijking, en incidenteel een kubische vergelijking, door middel van een geschikte substitutie. Volgens mij heb je me inderdaad ooit iets uitgelegd over wederkerige vergelijkingen toen we het probleem behandelden van die bol met een doorsnede a waarbij beide stukken die samen een halve bol vormden een gelijke inhoud hebben. Dat is alweer 'n poosje geleden, maar dat was deze post:

SPOILER

Om spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.

Wat betreft de techniek van het kwadraatafsplitsen, dit lijkt me nou een typisch gevalletje oefening baart kunst. Het ongeoefende oog ziet de juiste aanpak van zo'n probleem nu eenmaal minder snel..

Even wat heel anders. Ik probeerde deze opgave te maken:
Laat d₁ t/m d₁₂ reële getallen in het open interval (1, 12) zijn. Laat zien dat er verschillende indices i, j, k bestaan zodat d_i, d_j en d_k de lengtes van de zijden van een 'acute triangle' (een driehoek waarvan alle hoeken minder dan 90 graden zijn) zijn.

Ik stelde vervolgens de voorwaarden op dat drie gegeven reële getallen de lengtes van de zijden van een 'acute triangle' zijn. Neem c ≥ b ≥ a. Dan is a² + b² > c² een belangrijke voorwaarde, maar er moet ook gelden dat c < a + b, anders is er geen sprake van een driehoek.

Neem nu d_k = 10^12-k, met 1 ≤ k ≤ 12 Volgens mij bestaat er dan geen driehoek waarvan de zijden gelijk zijn aan een drietal van deze d_k's.

De d_k's worden dus steeds een factor 10 groter. Het is niet mogelijk een driehoek te tekenen met zijden van lengte a, b en c zodat c > 10b en b > 10a.

In het antwoord wordt de voorwaarde a + b > c helemaal niet genoemd.
Ik heb de vraag hier vandaan en de antwoorden hier.

Begrijp ik iets niet of klopt de vraag niet? Dat zou me nogal verbazen, het is best wel een prestigieuze wedstrijd had ik het idee.