SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
En als ze allemaal maar één keer voorkomen neem ik het hoogste getal ?quote:Op zaterdag 17 november 2012 01:21 schreef GlowMouse het volgende:
Kijk welke factoren je nodig hebt (bij elke priemfactor neem je het aantal dat het vaakste voorkomt bij één getal): driemaal een 2, tweemaal een 3, eenmaal een 7: 2*2*2*3*3*7 = 504.
Dit werkt omdat 2*2*2*3*3*7 deelbaar is door 3*3*7, door 2*3*7 en door 2*2*2*7.
Bij 78,39,65 is het bijvoorbeeld dit:
x2x3x13
x3x13
x5x13
Dit lijkt me dan niet te kloppen ? //edit, dit klopt dus wel, excuses.
Als ik achterin 5/78,5/39,3/65 op zoek geeft het boek 25/390,50/390,18/390 aan. Mis ik een stuk ?
[ Bericht 4% gewijzigd door obsama op 17-11-2012 01:35:53 ]
Je krijgt 2*3*5*13 als noemer, dat klopt toch?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Zij X_n een rij stochasten die convergeert naar X, en Y_n naar Y, waarbij (X_n) en (Y_n) onafhankelijk zijn. Geldt dan dat X en Y onafhankelijk zijn?
Nee, een tegenvoorbeeld is simpel te vinden (pak bijvoorbeeld X en Y constant).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik was inderdaad vergeten te noemen dat het over zwakke convergentie gaat (convergentie in distributie).
Het lukt me niet met een tegenvoorbeeld waar X en Y constant zijn.
Ik dacht misschien iets als X_n is uniform op [-1/n, 1/n] en Y_n uniform op [2-1/n, 2+1/n]. Dan geldt X=0, Y=2. Maar dan moet ik laten zien dat P(X<a, Y<b) niet gelijk is aan P(X<a)P(Y<b) voor bepaalde a en b, maar dat zie ik niet.
Ik dacht misschien iets als X_n is uniform op [-1/n, 1/n] en Y_n uniform op [2-1/n, 2+1/n]. Dan geldt X=0, Y=2. Maar dan moet ik laten zien dat P(X<a, Y<b) niet gelijk is aan P(X<a)P(Y<b) voor bepaalde a en b, maar dat zie ik niet.
Kijk voor welke a en b er 0 uitkomt, en wanneer er 1 uitkomt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hoe evalueer ik P(X<a, Y<b) als ik de joint density function niet weet? (en zolang je geen onafhankelijkheid hebt weet ik ook niet hoe ik die zou kunnen bepalen)quote:
Kijk voor welke a en b er 0 uitkomt, en wanneer er 1 uitkomt.
X en Y zijn constant, dan weet je de joint density
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
P(X ≤ a, Y ≤ b) = P(0 ≤ a, 2 ≤ b)quote:
X en Y zijn constant, dan weet je de joint density
= 1 als a ≥ 0 en b ≥ 2 en 0 anders
= P(X ≤ a) P(Y ≤ b)
[ Bericht 48% gewijzigd door thenxero op 18-11-2012 19:11:34 ]
Ik zoek toch een tegenvoorbeeld!quote:
Ik moet een opgave maken die dan en slechts dan mogelijk is als je kan bewijzen dat X en Y onafhankelijk zijn. Jij zegt dat het niet waar is maar ik kan geen tegenvoorbeeld vinden, maar ik kan het ook niet bewijzen. Laat maar eens jouw "eenvoudige" tegenvoorbeeld zien, ik ben benieuwd.
Ah constanten zijn inderdaad onafhankelijk, mijn fout. Kun je "(X_n) en (Y_n) onafhankelijk" nog iets verduidelijken? Geldt dit voor één N, of bedoel je hier de hele rij stochasten?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
(ik dacht al: zit je me nou te trollenquote:
Ah constanten zijn inderdaad onafhankelijk, mijn fout. Kun je "(X_n) en (Y_n) onafhankelijk" nog iets verduidelijken? Geldt dit voor één N, of bedoel je hier de hele rij stochasten?
)Die notatie betekent dat de hele rij stochasten onafhankelijk is: (X_n) staat voor
Hoe bewijs ik dat
.
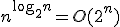Met n positieve gehele getallen.
Oftewel dat er een c > 0 is zodat er een N is zodat voor alle n > N geldt :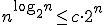
.
Je moet vast iets omschrijven maar het is lang geleden dat ik met andere logaritmes dan het natuurlijke logaritme heb gewerkt, dus ik zie het niet.
[ Bericht 0% gewijzigd door Anoonumos op 18-11-2012 22:40:08 ]
Met n positieve gehele getallen.
Oftewel dat er een c > 0 is zodat er een N is zodat voor alle n > N geldt :
Je moet vast iets omschrijven maar het is lang geleden dat ik met andere logaritmes dan het natuurlijke logaritme heb gewerkt, dus ik zie het niet.
[ Bericht 0% gewijzigd door Anoonumos op 18-11-2012 22:40:08 ]
Ik begrijp iets niet. In je ongelijkheid kan 2log x toch willekeurig groot worden door x voldoende groot te nemen? Dan kan er dus geen c zijn waarmee voor elke x > 0 aan je ongelijkheid wordt voldaan?quote:Op zondag 18 november 2012 22:01 schreef Anoonumos het volgende:
Hoe bewijs ik dat
Met n positieve gehele getallen.
Oftewel dat er een c > 0 is zodat er een N is zodat voor alle n > N geldt :.
Je moet vast iets omschrijven maar het is lang geleden dat ik met andere logaritmes dan het natuurlijke logaritme heb gewerkt, dus ik zie het niet.
Die x moet volgens mij gewoon een n zijn.quote:
[..]
Ik begrijp iets niet. In je ongelijkheid kan 2log x toch willekeurig groot worden door x voldoende groot te nemen? Dan kan er dus geen c zijn waarmee voor elke x > 0 aan je ongelijkheid wordt voldaan?
Dat ligt voor de hand, maar dat moet Anoonumos dan wel eerst bevestigen.quote:
[..]
Die x moet volgens mij gewoon een n zijn.
Je kan trouwens gewoon gebruiken dat log2 x = log x / log 2
En log 2 is constant, dus op zich werkt alles precies hetzelfde als bij de natuurlijke logaritme
En log 2 is constant, dus op zich werkt alles precies hetzelfde als bij de natuurlijke logaritme
Bedenk dat je hebt n = 2lb n, c = 2lb c etc. waar ik lb a schrijf voor 2log a (ISO recommendatie). Dan kun je je ongelijkheid omschrijven zodanig dat je links en rechts een macht van 2 krijgt. En als 2p ≤ 2q dan is p ≤ q. Daarmee zou het moeten lukken.quote:
Ja, excuses. Die x moet een n zijn. Ik zal het aanpassen.
Je bent me voor.quote:
[..]
Bedenk dat je hebt n = 2lb n, c = 2lb c etc. waar ik lb a schrijf voor 2log a (ISO recommendatie). Dan kun je je ongelijkheid omschrijven zodanig dat je links en rechts een macht van 2 krijgt. En als 2p ≤ 2q dan is p ≤ q. Daarmee zou het moeten lukken.
Het is toch iets trickier dan ik dacht. Je kunt direct links en rechts de binaire log nemen van de ongelijkheid:quote:
(1) nlb(n) ≤ c∙2n
en dan krijg je:
(2) (lb(n))2 ≤ lb(c) + n
Nu kun je gebruik maken van
(3) limn→∞ lb(n)/√n = 0
zodat er dus een N bestaat zodanig dat
(4) (lb(n))2 ≤ n voor elke n > N
Verder is voor elke c ≥ 1
(5) n ≤ lb(c) + n
en uit (4) en (5) volgt dan voor elke c ≥ 1 en n > N
(2) (lb(n))2 ≤ lb(c) + n
en dus ook (1), QED.
Ik snap de vraag niet goed. Als je hebt X=Y~N(0,1), en X_i, Y_i~N(0,1) allemaal onafhankelijk van de anderen, wat gaat er dan mis?quote:
Zij X_n een rij stochasten die convergeert naar X, en Y_n naar Y, waarbij (X_n) en (Y_n) onafhankelijk zijn. Geldt dan dat X en Y onafhankelijk zijn?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ja, zo was het mij uiteindelijk ook gelukt.quote:
[..]
Het is toch iets trickier dan ik dacht. Je kunt direct links en rechts de binaire log nemen van de ongelijkheid:
..
en dus ook (1), QED.
Hartelijk dank.
Zo had ik het niet bedacht. Ik zou n=2m substirueren, dat is volgens mij wat makkelijker.quote:
[..]
Het is toch iets trickier dan ik dacht. Je kunt direct links en rechts de binaire log nemen van de ongelijkheid:
(1) nlb(n) ≤ c∙2n
en dan krijg je:
(2) (lb(n))2 ≤ lb(c) + n
Nu kun je gebruik maken van
(3) limn→∞ lb(n)/√n = 0
zodat er dus een N bestaat zodanig dat
(4) (lb(n))2 ≤ n voor elke n > N
Verder is voor elke c ≥ 1
(5) n ≤ lb(c) + n
en uit (4) en (5) volgt dan voor elke c ≥ 1 en n > N
(2) (lb(n))2 ≤ lb(c) + n
en dus ook (1), QED.
Laat eens precies zien hoe je dan verder gaat? Met jouw substitutie krijg je in het rechterlid van de ongelijkheid een macht van een macht. Ik zie niet hoe dat gemakkelijker zou zijn. Ook heb ik het idee dat je vergeet dat m dan niet uitsluitend geheel kan zijn.quote:Op maandag 19 november 2012 08:38 schreef kutkloon7 het volgende:
[..]
Zo had ik het niet bedacht. Ik zou n=2m substitueren, dat is volgens mij wat makkelijker.
Dan gaat er niks mis. De vraag is eigenlijk of onafhankelijkheid overeind blijft in de limiet. Je weet dat de X_i en de Y_i allemaal onafhankelijk zijn, maar geldt dat nog steeds in de limiet? D.w.z.: geldt ook X onafhankelijk van Y (als dat nog niet gesteld is).quote:
[..]
Ik snap de vraag niet goed. Als je hebt X=Y~N(0,1), en X_i, Y_i~N(0,1) allemaal onafhankelijk van de anderen, wat gaat er dan mis?
Ik heb X=Y gekozen.quote:
[..]
Dan gaat er niks mis. De vraag is eigenlijk of onafhankelijkheid overeind blijft in de limiet. Je weet dat de X_i en de Y_i allemaal onafhankelijk zijn, maar geldt dat nog steeds in de limiet? D.w.z.: geldt ook X onafhankelijk van Y (als dat nog niet gesteld is).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oh dat zie ik nu pasquote:
. Ik weet niet of je dat zo kan definiëren. Het klopt dat X_n gaat naar X, Y_n naar Y in distributie. Maar of je de limieten zo aan elkaar gelijk kan kiezen? Hmmm....
Het is me nog steeds niet duidelijk wat de vraag precies is. Misschien moet je even een stap terug doen en daar nog eens over nadenken.
Je kan wel termen noemen als "tegengestelde" of "additieve inverse", maar "g(x)=-f(x)" lijkt me in vrijwel alle gevallen het duidelijkst, dus ik zou het geen naam geven.quote:Op maandag 19 november 2012 12:52 schreef Dale. het volgende:
Ik heb een functie f(x) en een functie g(x), g(x) is in feite -f(x), heeft dat een naam?
Wat is er precies onduidelijk aan?quote:
Het is me nog steeds niet duidelijk wat de vraag precies is. Misschien moet je even een stap terug doen en daar nog eens over nadenken.
Klopt, ik was in de war. Ik dacht even dat (2m)2 = 2m*m, dan zou het volgens mij een stuk makkelijker kunnen. He, denk ik ook eens wat te wetenquote:
[..]
Laat eens precies zien hoe je dan verder gaat? Met jouw substitutie krijg je in het rechterlid van de ongelijkheid een macht van een macht. Ik zie niet hoe dat gemakkelijker zou zijn. Ook heb ik het idee dat je vergeet dat m dan niet uitsluitend geheel kan zijn.
. Nevermind.
Kan iemand mij iets duidelijk maken omtrent quotientruimte, restklassen etc? Als voorbeeld deze vraag. Waar begin ik met denken? Hoe bewijs je het vanzelfsprekende? Mijn antwoord is nu zoiets als: dat zie je toch? Helaas volstaat dat niet in Lineaire Algebra 
Pff, wat ben ik alles van lineaire algebra B snel vergeten. In ieder geval moet je laten zien dat elke vector in V/U uitgedrukt kan worden als lineaire combinatie van de vectoren vr+1 + U, ..., vn + U. Ik weet niet of je hier wat aan hebt?quote:
Kan iemand mij iets duidelijk maken omtrent quotientruimte, restklassen etc? Als voorbeeld deze vraag. Waar begin ik met denken? Hoe bewijs je het vanzelfsprekende? Mijn antwoord is nu zoiets als: dat zie je toch? Helaas volstaat dat niet in Lineaire Algebra
(Ik moet bekennen dat ik het begrip quotiëntruimte van een lineaire ruimte niet ken, volgens mij is die nooit in het college behandeld bij ons, en de notatie vr + U ook niet)
Kan iemand me vertellen waar die tot de 3e macht vandaan komt?
Blues ain't nothing but a good man feeling bad...
Kettingregel.quote:
[ afbeelding ]
Kan iemand me vertellen waar die tot de 3e macht vandaan komt?
Ik moet de inverse laplacegettransformeerde van -2/((s+3)^2) hebben, maar kom er niet helemaal uit.
Het antwoord zou -2te^(-3t) moeten zijn.
Kan iemand mij helpen?
Welke stappen of standaardtransformaties gebruiken ze?
Het antwoord zou -2te^(-3t) moeten zijn.
Kan iemand mij helpen?
Welke stappen of standaardtransformaties gebruiken ze?
Ik neem aan dat ze niet verwachten dat je met de inversieformules van Mellin of Post aan de slag gaat, dus zal het de bedoeling zijn om gewoon je standaardtabelletje met Laplace transformaties te gebruiken.quote:
Ik moet de inverse laplacegettransformeerde van -2/((s+3)^2) hebben, maar kom er niet helemaal uit.
Het antwoord zou -2te^(-3t) moeten zijn.
Kan iemand mij helpen?
Welke stappen of standaardtransformaties gebruiken ze?
Dankje. Lineaire Algebra wordt hoogstwaarschijnlijke reden #1 dat ik gedwongen wordt te stoppen met Natuurkundequote:
[..]
Pff, wat ben ik alles van lineaire algebra B snel vergeten. In ieder geval moet je laten zien dat elke vector in V/U uitgedrukt kan worden als lineaire combinatie van de vectoren vr+1 + U, ..., vn + U. Ik weet niet of je hier wat aan hebt?
(Ik moet bekennen dat ik het begrip quotiëntruimte van een lineaire ruimte niet ken, volgens mij is die nooit in het college behandeld bij ons, en de notatie vr + U ook niet)
Ik ben bezig met een onderzoek, en nu wil het geval dat mijn databestand de volledige onderzoekspopulatie beslaat. Ik heb bij vakken over statistiek echter altijd geleerd dat je statistiek gebruikt als je op basis van een sample uitspraken wil doen over de totale populatie, maar in dit geval is mijn sample dus gelijk aan de totale populatie. Zit ik dan goed met de gedachte dat ik geen statistische toetsen meer hoef te gebruiken om bijvoorbeeld te kunnen stellen dat geval A vaker voor komt dan geval B? Ik kan immers gewoon in de totale populatie kijken en daadwerkelijk vaststellen door middel van tellen dat geval A vaker voor komt dan geval B.
Ga je het vak niet halen? Als je denkt dat je de studie voor de rest wel aankan, zou ik er gewoon wat wiskunde bijles tegenaan gooien.quote:
[..]
Dankje. Lineaire Algebra wordt hoogstwaarschijnlijke reden #1 dat ik gedwongen wordt te stoppen met Natuurkunde
Wel, je moet twee dingen aantonen:quote:
Kan iemand mij iets duidelijk maken omtrent quotientruimte, restklassen etc? Als voorbeeld deze vraag. Waar begin ik met denken? Hoe bewijs je het vanzelfsprekende? Mijn antwoord is nu zoiets als: dat zie je toch? Helaas volstaat dat niet in Lineaire Algebra
(a) de gegeven elementen zijn lineair onafhankelijk in V/U
(b) spannen V/U op
Ik zal (a) voordoen, dan mag je zelf (b) doen.
(a) Stel ze zijn afhankelijk. Dan zijn er cr+1, ..., cn in F, niet allemaal 0, met somi>rci(vi + U) = 0 in V/U. Dat betekent niks anders dan dat somi>rcivi in U zit, en dus is dat een lineaire combinatie van v1, ..., vr. Er zijn dus d1, ..., dr in F met somi<=rdivi = somi>rcivi. Maar de vi vormen een basis voor V, dus ze zijn linear onafhankelijk, dus zo'n relatie kan niet bestaan.
Ik heb elke dag van half 9 tot half 6 colleges en op donderdag zelfs tot half 7. Als ik het daarmee niet redt (thuis ook nog zelfstudie) is het voor mij een groot genoeg teken dat ik er maar beter mee kan kappenquote:
[..]
Ga je het vak niet halen? Als je denkt dat je de studie voor de rest wel aankan, zou ik er gewoon wat wiskunde bijles tegenaan gooien.
Twee studies?quote:Op woensdag 21 november 2012 19:07 schreef Crisisstudent het volgende:
[..]
Ik heb elke dag van half 9 tot half 6 colleges en op donderdag zelfs tot half 7. Als ik het daarmee niet redt (thuis ook nog zelfstudie) is het voor mij een groot genoeg teken dat ik er maar beter mee kan kappen
