SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
is f continu op
Ik kan laten zien dat f continu is op x=-1 en x=2, maar hoe laat ik zien dat f continu (of niet) is op zo'n open interval?
Alvast bedankt
Heb je een stelling die zegt dat wortels continu zijn? En polynomen? etc
Om dit helemaal met een epsilon delta bewijs te doen is niet makkelijk, maar met zulke stellingen voorhanden ben je zo klaar.
Om dit helemaal met een epsilon delta bewijs te doen is niet makkelijk, maar met zulke stellingen voorhanden ben je zo klaar.
Ze zeggen hier:
sin(x+y) = sin(x)*cos(y) + cos(x)*sin(y)
Maar wat is y?
Hiervoor werd er alleen gebruikt van:
Sin(1/3pi) = de y coordinaat van het punt in de bovenste hoek etc.
Maar nu gaan ze x+y doen? Ik dacht dat je bij sin een hoek moest invullen? Wat is X dan en wat is Y?
sin(x+y) = sin(x)*cos(y) + cos(x)*sin(y)
Maar wat is y?
Hiervoor werd er alleen gebruikt van:
Sin(1/3pi) = de y coordinaat van het punt in de bovenste hoek etc.
Maar nu gaan ze x+y doen? Ik dacht dat je bij sin een hoek moest invullen? Wat is X dan en wat is Y?
When I get sad, I stop being sad and just be awesome instead.
Ja die heb ik, ik mag zeggen dat polynomen continu zijn op hun domein en wortels ook(zolang de uitdrukking binnen de wortel groter of gelijk is aan 0)quote:Op zondag 23 september 2012 16:56 schreef thenxero het volgende:
Heb je een stelling die zegt dat wortels continu zijn? En polynomen? etc
Om dit helemaal met een epsilon delta bewijs te doen is niet makkelijk, maar met zulke stellingen voorhanden ben je zo klaar.
Ook weet ik dat de functie niet continu is op x=1 zelf, maar hoe laat ik zien dat ie op elk ander punt wel continu is?quote:
Heb je een stelling die zegt dat wortels continu zijn? En polynomen? etc
Om dit helemaal met een epsilon delta bewijs te doen is niet makkelijk, maar met zulke stellingen voorhanden ben je zo klaar.
De regel die je hier geeft voor de sinus van de som van twee hoeken (resp. rotaties) is een zogeheten additietheorema. Ik ben er zelf niet voor om de (rotatie)hoeken aan te duiden met x of y, want dit geeft vaak aanleiding tot begripsverwarring, dat blijkt hier wel weer.quote:
Ze zeggen hier:
sin(x+y) = sin(x)*cos(y) + cos(x)*sin(y)
Maar wat is y?
Hiervoor werd er alleen gebruikt van:
Sin(1/3pi) = de y coordinaat van het punt in de bovenste hoek etc.
Maar nu gaan ze x+y doen? Ik dacht dat je bij sin een hoek moest invullen? Wat is X dan en wat is Y?
De sinus van een (rotatie)hoek is meetkundig gedefinieerd als de y-coördinaat van het beeldpunt van (1;0) bij rotatie om de oorsprong over de gegeven hoek. Drukken we deze (rotatie)hoek uit in radialen, dan geldt bijvoorbeeld sin(π/3) = ½√3. Het is beter om Griekse kleine letters te gebruiken voor rotatiehoeken, dan kun je bijvoorbeeld schrijven:
cos(α+β) = cos α∙cos β - sin α∙sin β
sin(α+β) = sin α∙cos β + cos α∙sin β
Als je een bewijs wil zien voor deze identiteiten, dan moet je dit maar eens bestuderen.
Je hoeft feitelijk alleen nog maar de continuïteit van je functie aan te tonen voor x = -1 en x = 2.quote:
[..]
Ook weet ik dat de functie niet continu is op x=1 zelf, maar hoe laat ik zien dat ie op elk ander punt wel continu is?
Dat maakt het veel duidelijker, dank jequote:
[..]
De regel die je hier geeft voor de sinus van de som van twee hoeken (resp. rotaties) is een zogeheten additietheorema. Ik ben er zelf niet voor om de (rotatie)hoeken aan te duiden met x of y, want dit geeft vaak aanleiding tot begripsverwarring, dat blijkt hier wel weer.
De sinus van een (rotatie)hoek is meetkundig gedefinieerd als de y-coördinaat van het beeldpunt van (1;0) bij rotatie om de oorsprong over de gegeven hoek. Drukken we deze (rotatie)hoek uit in radialen, dan geldt bijvoorbeeld sin(π/3) = ½√3. Het is beter om Griekse kleine letters te gebruiken voor rotatiehoeken, dan kun je bijvoorbeeld schrijven:
cos(α+β) = cos α∙cos β - sin α∙sin β
sin(α+β) = sin α∙cos β + cos α∙sin β
Als je een bewijs wil zien voor deze identiteiten, dan moet je dit maar eens bestuderen.
When I get sad, I stop being sad and just be awesome instead.
Dan ben je er toch? Je moet continuïteit op x=-1 checken omdat je daar eigenlijk van de ene op de andere functie overstapt. Dan moeten de boven en onderlimiet wel dezelfde waardes geven. Op x=1 hoef je niet te kijken vanwege de vraagstelling, en op x=2 moet je even checken omdat je daar een punt toevoegt. De stellingen garanderen continuïteit op de rest van R.quote:
[..]
Ja die heb ik, ik mag zeggen dat polynomen continu zijn op hun domein en wortels ook(zolang de uitdrukking binnen de wortel groter of gelijk is aan 0)
Beste mensen,
ik heb nog 3 vragen waar ik bepaalde stappen van niet begrijp: http://i.imgur.com/QPaDb.jpg
Vraag 4, 5 en 6.
Laat ik bij vraag 4 beginnen. Ik heb gegoogled op de change-of-base formule. Echter zijn alle voorbeelden die ik daar zie simpele gevallen zoals 3log(x) en deze is wat moeilijker. Hoe pas ik deze formule hier toe?
Vraag 5: bij de laatste stap is ln9 opeens weg (woprdt niet vereenvoudigd) en wordt ln3 een negatief getal (-1/5 ln3). Waarom? Wat gebeurt hier?
Vraag 6: Waarom verdwijnt (1/2) opeens en verandert 9x in -9x?
Sorry dat ik jullie lastigval met deze vragen. Ik lees de boeken door, maar vind dat het allemaal erg vaag is. Aan feedback van studiegenoten te horen ben ik niet de enige. Weet je iets niet, ben je fucked, of mag je lekker in de rij staan bij een werkcollege, wat eens per week is.
--
ik heb nog 3 vragen waar ik bepaalde stappen van niet begrijp: http://i.imgur.com/QPaDb.jpg
Vraag 4, 5 en 6.
Laat ik bij vraag 4 beginnen. Ik heb gegoogled op de change-of-base formule. Echter zijn alle voorbeelden die ik daar zie simpele gevallen zoals 3log(x) en deze is wat moeilijker. Hoe pas ik deze formule hier toe?
Vraag 5: bij de laatste stap is ln9 opeens weg (woprdt niet vereenvoudigd) en wordt ln3 een negatief getal (-1/5 ln3). Waarom? Wat gebeurt hier?
Vraag 6: Waarom verdwijnt (1/2) opeens en verandert 9x in -9x?
Sorry dat ik jullie lastigval met deze vragen. Ik lees de boeken door, maar vind dat het allemaal erg vaag is. Aan feedback van studiegenoten te horen ben ik niet de enige. Weet je iets niet, ben je fucked, of mag je lekker in de rij staan bij een werkcollege, wat eens per week is.
--
vraag 4: Ik zou de 3*9log(x) omzetten naar een log met grondtal 3.
2*3log(x) - 3*9log(x) = 3
2*3log(x) - 3*3log(x)/3log(9) = 3
2*3log(x) - 3*3log(x)/2 = 3 ......... (Remembert; 3log(9) = 2 want 3*3 = 32 = 9)
2*3log(x) - (3/2)*3log(x) = 3
(1/2)*3log(x) = 3
3log(x) = 6
36 = x = 729
Vraag 5: dat hebben ze idioot ranzig uitgelegd zeg
. Zou ik nooit zo doen. Wat ik zou doen is:
e5x-1 = 3/9 = 1/3 =3-1 => 5x-1 = ln(3-1) => 5x-1 = -ln3 => 5x = 1 - ln3 => x = (1 - ln3)/5
Vraag6: ik zou het grondtal (1/2) omzetten naar een echte macht van 2, nl. 2-1. dan krijg je 2x+4 = (1/2)9-2x = 22x-9
[ Bericht 6% gewijzigd door VanishedEntity op 24-09-2012 01:48:27 ]
2*3log(x) - 3*9log(x) = 3
2*3log(x) - 3*3log(x)/3log(9) = 3
2*3log(x) - 3*3log(x)/2 = 3 ......... (Remembert; 3log(9) = 2 want 3*3 = 32 = 9)
2*3log(x) - (3/2)*3log(x) = 3
(1/2)*3log(x) = 3
3log(x) = 6
36 = x = 729
Vraag 5: dat hebben ze idioot ranzig uitgelegd zeg
. Zou ik nooit zo doen. Wat ik zou doen is: e5x-1 = 3/9 = 1/3 =3-1 => 5x-1 = ln(3-1) => 5x-1 = -ln3 => 5x = 1 - ln3 => x = (1 - ln3)/5
Vraag6: ik zou het grondtal (1/2) omzetten naar een echte macht van 2, nl. 2-1. dan krijg je 2x+4 = (1/2)9-2x = 22x-9
[ Bericht 6% gewijzigd door VanishedEntity op 24-09-2012 01:48:27 ]
En vraag 5: Ln(3)-ln(9) = Ln(3)-Ln(32) = Ln(3)-2Ln(3) = -Ln(3)quote:
Beste mensen,
ik heb nog 3 vragen waar ik bepaalde stappen van niet begrijp: http://i.imgur.com/QPaDb.jpg
Vraag 4, 5 en 6.
Laat ik bij vraag 4 beginnen. Ik heb gegoogled op de change-of-base formule. Echter zijn alle voorbeelden die ik daar zie simpele gevallen zoals 3log(x) en deze is wat moeilijker. Hoe pas ik deze formule hier toe?
Vraag 5: bij de laatste stap is ln9 opeens weg (woprdt niet vereenvoudigd) en wordt ln3 een negatief getal (-1/5 ln3). Waarom? Wat gebeurt hier?
Vraag 6: Waarom verdwijnt (1/2) opeens en verandert 9x in -9x?
Sorry dat ik jullie lastigval met deze vragen. Ik lees de boeken door, maar vind dat het allemaal erg vaag is. Aan feedback van studiegenoten te horen ben ik niet de enige. Weet je iets niet, ben je fucked, of mag je lekker in de rij staan bij een werkcollege, wat eens per week is.
--
Vraag 6: (1/2)9-2x = (2-1)9-2x = 2-1*(9-2x) = 2-9+2x
26"
Fading slowly.
Fading slowly.
Er is echt niets vaags aan, en moeilijk is het ook niet. Dit had je allemaal op school moeten leren. Afgaande op je posts hier op FOK van de laatste tijd denk ik dat je gewoon een hoop essentiële basiskennis mist voor de opleiding die je bent gaan doen.quote:
Beste mensen,
ik heb nog 3 vragen waar ik bepaalde stappen van niet begrijp: http://i.imgur.com/QPaDb.jpg
Vraag 4, 5 en 6.
Laat ik bij vraag 4 beginnen. Ik heb gegoogled op de change-of-base formule. Echter zijn alle voorbeelden die ik daar zie simpele gevallen zoals 3log(x) en deze is wat moeilijker. Hoe pas ik deze formule hier toe?
Vraag 5: bij de laatste stap is ln9 opeens weg (wordt niet vereenvoudigd) en wordt ln3 een negatief getal (-1/5 ln3). Waarom? Wat gebeurt hier?
Vraag 6: Waarom verdwijnt (1/2) opeens en verandert 9x in -9x?
Sorry dat ik jullie lastigval met deze vragen. Ik lees de boeken door, maar vind dat het allemaal erg vaag is. Aan feedback van studiegenoten te horen ben ik niet de enige. Weet je iets niet, ben je fucked, of mag je lekker in de rij staan bij een werkcollege, wat eens per week is.
--
Nou, ze laten daar wel een aantal stappen weg waardoor het voor een beginner ook zomaar uit de lucht lijkt te komen vallen. Zie mn opmerking over vraag 5; daar gaan ze in 1 keer van 5x-1 = ln(3/9) = ln3 - ln9 naar x = 1/5 - (1/5)*ln3 zonder de tussenstappen 5x-1 = ln(3/9) = ln(1/3) = ln(3-1) => 5x-1 = -ln3 => 5x = 1 - ln3 te laten zien.
Maar ik deel je conclusie dat eMazing teveel basiskennis ontbeert voor zn huidige opleiding, want deze opgaven moet je zonder veel moeite tot een goed einde kunnen brengen.
Maar ik deel je conclusie dat eMazing teveel basiskennis ontbeert voor zn huidige opleiding, want deze opgaven moet je zonder veel moeite tot een goed einde kunnen brengen.
Essentiele basiskennis die misschien niet zo essentieel bleek voor mensen met wiskunde a. Toch bedankt.quote:
[..]
Er is echt niets vaags aan, en moeilijk is het ook niet. Dit had je allemaal op school moeten leren. Afgaande op je posts hier op FOK van de laatste tijd denk ik dat je gewoon een hoop essentiële basiskennis mist voor de opleiding die je bent gaan doen.
Tja, dan denk ik toch dat ze mensen die op school niet genoeg wiskunde hebben gedaan (lees: alleen wiskunde A) maar toch aan een opleiding willen beginnen met een aardige dosis wiskunde eerst een toelatingsexamen zouden moeten laten afleggen, of gewoon niet zouden moeten toelaten. Misschien denk je nu dat het even een paar weken doorbijten is en dat het dan verder allemaal smooth sailing wordt, maar dat is niet zo, het gebrek aan een solide basis zal je verderop ook opbreken.quote:
[..]
Essentiele basiskennis die misschien niet zo essentieel bleek voor mensen met wiskunde a. Toch bedankt.
quote:
[..]
Tja, dan denk ik toch dat ze mensen die op school niet genoeg wiskunde hebben gedaan (lees: alleen wiskunde A) maar toch aan een opleiding willen beginnen met een aardige dosis wiskunde eerst een toelatingsexamen zouden moeten laten afleggen, of gewoon niet zouden moeten toelaten. Misschien denk je nu dat het even een paar weken doorbijten is en dat het dan verder allemaal smooth sailing wordt, maar dat is niet zo, het gebrek aan een solide basis zal je verderop ook opbreken.
Dank jullie wel.quote:
vraag 4: Ik zou de 3*9log(x) omzetten naar een log met grondtal 3.
2*3log(x) - 3*9log(x) = 3
2*3log(x) - 3*3log(x)/9log(3) = 3
2*3log(x) - 3*3log(x)/2 = 3 ......... (Remembert; 9log(3) = 2 want 3*3 = 32 = 9)
2*3log(x) - (3/2)*3log(x) = 3
(1/2)*3log(x) = 3
3log(x) = 6
36 = x = 729
Vraag 5: dat hebben ze idioot ranzig uitgelegd zeg
e5x-1 = 3/9 = 1/3 =3-1 => 5x-1 = ln(3-1) => 5x-1 = -ln3 => 5x = 1 - ln3 => x = (1 - ln3)/5
Vraag6: ik zou het grondtal (1/2) omzetten naar een echte macht van 2, nl. 2-1. dan krijg je 2x+4 = (1/2)9-2x = 22x-9
Ik snap dat mijn basiskennis inderdaad achterloopt. Echter kan ik het beter proberen te snappen. Het probleem ligt hem namelijk in het feit dat het niet duidelijk wordt uitgelegd. Nu snap ik deze dingen dus wel.
--
Zou je me deze stap uit kunnen leggen? Wat is de logica dat je opeens bij een quotient komt bij die 2e log?quote:
vraag 4: Ik zou de 3*9log(x) omzetten naar een log met grondtal 3.
2*3log(x) - 3*9log(x) = 3
2*3log(x) - 3*3log(x)/9log(3) = 3
2*3log(x) - 3*3log(x)/2 = 3 ......... (Remembert; 9log(3) = 2 want 3*3 = 32 = 9)
2*3log(x) - (3/2)*3log(x) = 3
(1/2)*3log(x) = 3
3log(x) = 6
36 = x = 729
cht van 2, nl. 2-1. dan krijg je 2x+4 = (1/2)9-2x = 22x-9
Dat is weer gewoon de rekenregel voor het veranderen van het grondtal van een logaritme toepassen, alleen doet VanishedEntity het wel verkeerd om. We hebben:quote:
[..]
Zou je me deze stap uit kunnen leggen? Wat is de logica dat je opeens bij een quotient komt bij die 2e log?
blog a = glog a / glog b
Hier is b = 9, a = x, g = 3, dus hebben we:
9log x = 3log x / 3log 9 = ½∙3log x
Je kunt bovenstaande rekenregel ook in de volgende elegante vorm opschrijven, die je wellicht beter kunt onthouden:
glog b ∙ blog a = glog a
Voor een beter begip van deze regel is het goed om eens te zien waarom deze regel eigenlijk geldt. Laten we zeggen dat:
(1) glog b = x en blog a = y
Volgens de definitie van de logaritme is glog b de macht waartoe je g moet verheffen om b te krijgen en is blog a de macht waartoe je b moet verheffen om a te krijgen. Dus is (1) equivalent met:
(2) gx = b en by = a
Maar dan geldt dus:
(3) (gx)y = by = a
Maar aangezien volgens de rekenregels voor machten geldt:
(4) (gx)y = gxy
hebben we dus:
(5) gxy = a
Maar als je nu g tot de macht xy moet verheffen om a te krijgen dan betekent dit volgens de definitie van de logaritme niets anders dan:
(6) xy = glog a
En aangezien volgens (1) x = glog b en y = blog a kunnen we voor (6) dus schrijven:
(7) glog b ∙ blog a = glog a
Aangezien b ≠ 1 en dus glog b ≠ 0 kunnen we beide leden van (7) delen door glog b en krijgen we inderdaad:
(8) blog a = glog a / glog b
Je ziet dus dat (7) en daarmee ook (8) niets anders is dan een eenvoudige consequentie van de bekende rekenregel (4) voor machten en de definitie van de logaritme.
We maken hier gebruik van de techniek/formule van/voor het veranderen grondtallen van logaritmen;
blog(x) = alog(x)/alog(b).
Op die manier kunnen we die vervelende 3*9log(x) herschrijven naar eentje met grondtal 3 zodat er aan de linkerkant van de vgl. er veul makkelijker mee te werken valt. Zodoende komen we van 3*9log(x) op 3*3log(x) / 3log(9) oftewel 3*3log(x)/2 .
PS: aub ook even de lijnen
2*3log(x) - 3*3log(x)/9log(3) = 3
2*3log(x) - 3*3log(x)/2 = 3 ......... (Remembert; 9log(3) = 2 want 3*3 = 32 = 9)
verbeteren naar
2*3log(x) - 3*3log(x)/3log(9) = 3
2*3log(x) - 3*3log(x)/2 = 3 ......... (Remembert; 3log(9) = 2 want 3*3 = 32 = 9)
in de door jouw gequootte replies van mij in de jouwe.
blog(x) = alog(x)/alog(b).
Op die manier kunnen we die vervelende 3*9log(x) herschrijven naar eentje met grondtal 3 zodat er aan de linkerkant van de vgl. er veul makkelijker mee te werken valt. Zodoende komen we van 3*9log(x) op 3*3log(x) / 3log(9) oftewel 3*3log(x)/2 .
PS: aub ook even de lijnen
2*3log(x) - 3*3log(x)/9log(3) = 3
2*3log(x) - 3*3log(x)/2 = 3 ......... (Remembert; 9log(3) = 2 want 3*3 = 32 = 9)
verbeteren naar
2*3log(x) - 3*3log(x)/3log(9) = 3
2*3log(x) - 3*3log(x)/2 = 3 ......... (Remembert; 3log(9) = 2 want 3*3 = 32 = 9)
in de door jouw gequootte replies van mij in de jouwe.
Weet iemand hoe je dit moet intypen in je rekenmachine?
e^ 1(4.2)(0.5)
Waar staat dat die E voor? ik kom daar niet uit...
e^ 1(4.2)(0.5)
Waar staat dat die E voor? ik kom daar niet uit...
e is het getal van Euler.
Als het je boeit:
Stel dat f(x) = ax
Stel dat f'(x) = ax
Dan geldt:
a = e ≈ 2,72
En wat je macht betreft, dat begrijp ik niet helemaal. e zit boven je deeltoets op je GR. second dus.
Wat bedoel je met je macht?
[ Bericht 11% gewijzigd door #ANONIEM op 24-09-2012 12:22:09 ]
Als het je boeit:
Stel dat f(x) = ax
Stel dat f'(x) = ax
Dan geldt:
a = e ≈ 2,72
En wat je macht betreft, dat begrijp ik niet helemaal. e zit boven je deeltoets op je GR. second dus.
Wat bedoel je met je macht?
[ Bericht 11% gewijzigd door #ANONIEM op 24-09-2012 12:22:09 ]
Nou, het is eigenlijk van statistiek en de formule is..
P(X>30) = e ^(-Lambda * x) = e ^-(4.2) (0.5) = 0.1225
Het gemiddelde is 4.2
Maar het punt is, ik begrijp niet wat ik voor die E moet invullen, ik neem aan dat er een getal ofzo moet komen te staan?
P(X>30) = e ^(-Lambda * x) = e ^-(4.2) (0.5) = 0.1225
Het gemiddelde is 4.2
Maar het punt is, ik begrijp niet wat ik voor die E moet invullen, ik neem aan dat er een getal ofzo moet komen te staan?
Wat heb jij een achterlijk kutte notatie zeg.quote:
Nou, het is eigenlijk van statistiek en de formule is..
P(X>30) = e ^(-Lambda * x) = e ^-(4.2) (0.5) = 0.1225
Het gemiddelde is 4.2
Maar het punt is, ik begrijp niet wat ik voor die E moet invullen, ik neem aan dat er een getal ofzo moet komen te staan?
e-λ * x
Waarbij geldt:
λ = 4.2
x = ½
Dan schrijf je:
e-4.2 * ½. = e-2.1 ≈ 0,1225
Ook dit is niet waar!quote:
e ≈ 2.71828
Getal van Euler
Lees dat eens door als je tot een beter inzicht betreffende het getal van Euler wilt komen.
[ Bericht 1% gewijzigd door #ANONIEM op 24-09-2012 12:30:38 ]
Jawel, sorry was onduidelijk want ben beetje in de stress. Maar e is in mijn geval natuurlijke logaritme (poisson verdeling).
13.75 - X
0.613= ________
6
x= 10.07
Hoe kan je berekenen dat X 10.07 is?
13.75 - X
0.613= ________
6
x= 10.07
Hoe kan je berekenen dat X 10.07 is?
Je gaat die formule omschrijven totdat dat X aan de rechterkant overblijft.quote:
ggrrr
ik bedoel dus
0.613 = 13.75 - X / 6
X= 10.07
0.613 = ( 13.75 - X ) / 6
1) Eerst wil je die 6 weghebben. Het tegenovergesteld van delen is vermenigvuldiggen. Dus de rechterkant vermendivuldig je met 6. En pief paf poef, weg is de 6.
Maarrrr, wat je rechts doet moet je links ook doen. dus:
0,613 * 6 = 13,75 - X
Dit heb je nu.
2) 13,75 naar de andere kant halen, dat is dus aan beide kanten 13,75 erafhalen:
(0,613 * 6 ) - 13,75 = - X
-10.072 = -X
oftewel X = 10,072
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Blues ain't nothing but a good man feeling bad...
En je vergelijking correct opschrijven.
Nu lijkt er te staan:
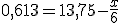
[ Bericht 0% gewijzigd door #ANONIEM op 24-09-2012 16:22:18 ]
Nu lijkt er te staan:
[ Bericht 0% gewijzigd door #ANONIEM op 24-09-2012 16:22:18 ]
Ok, ik kom er totaal niet meer uit, werk de haakjes uit en vereenvoudig: (a-b)^4 + (a+b)^4
Wat ik op papier heb:
= a(a^3 + 3a^2b + 3ab^2 + b^3) -b(a^3 + 3a^2b + 3ab^2 +b^3) a(a^3 + 3a^2b + 3ab^2 +b^3) b(a^3 + 3a^2b + 3ab^2 +b^3)
= a^4 +3a^3b +3a^2b^2 + ab^3 -a^3b -3a^2b^2 -3ab^3 -b^4 +a^4 +3a^3b +3a^2b^2 +ab^3 +a^3b +3a^2b^2 +3ab^3 +b^4
Ik krijg zo het idee dat dit makkelijker moet kunnen. (als het ál klopt wat ik ervan gemaakt heb)...
Wat ik op papier heb:
= a(a^3 + 3a^2b + 3ab^2 + b^3) -b(a^3 + 3a^2b + 3ab^2 +b^3) a(a^3 + 3a^2b + 3ab^2 +b^3) b(a^3 + 3a^2b + 3ab^2 +b^3)
= a^4 +3a^3b +3a^2b^2 + ab^3 -a^3b -3a^2b^2 -3ab^3 -b^4 +a^4 +3a^3b +3a^2b^2 +ab^3 +a^3b +3a^2b^2 +3ab^3 +b^4
Ik krijg zo het idee dat dit makkelijker moet kunnen. (als het ál klopt wat ik ervan gemaakt heb)...
Gebruik de driehoek van Pascal voor die binomiale expansies; dan krijg je voor de linkerterm
a4 +4*a3b +6*a2b2 +4*ab3 +b4
en voor de rechterterm
a4 -4*a3b +6*a2b2 -4*ab3 +b4
bij elkaar optellen levert dan 2a4 + 12a2b2 + 2b4 op.
a4 +4*a3b +6*a2b2 +4*ab3 +b4
en voor de rechterterm
a4 -4*a3b +6*a2b2 -4*ab3 +b4
bij elkaar optellen levert dan 2a4 + 12a2b2 + 2b4 op.
Aha, dat wordt even goed studeren zie ik! Dankje!
Edit: Het valt mee, snap em! Nogmaals dank
[ Bericht 30% gewijzigd door DeGemaskerdeMuchacho op 24-09-2012 19:27:37 ]
Edit: Het valt mee, snap em! Nogmaals dank
[ Bericht 30% gewijzigd door DeGemaskerdeMuchacho op 24-09-2012 19:27:37 ]
Eigenlijk is het natuurkunde maar goed, het heeft betrekking tot wiskunde. In mijn boek hebben ze het over coödinatentransformatie, dus hoe je van een kromme lijn een rechte maakt, zodat je de constante uit een grafiek kan halen. Dit doen ze door 1 gedeeld door x te doen. Als voorbeeld nemen ze een omgekeerd evenredig verband dus:
y=c/x >> y=c*(1/x)
Maar waarom mag dit? Hoe komen ze opeens bij die 1/x?
y=c/x >> y=c*(1/x)
Maar waarom mag dit? Hoe komen ze opeens bij die 1/x?
Delen door een breuk is hetzelfde als vermenigvuldigen met het omgekeerde:quote:
Eigenlijk is het natuurkunde maar goed, het heeft betrekking tot wiskunde. In mijn boek hebben ze het over coödinatentransformatie, dus hoe je van een kromme lijn een rechte maakt, zodat je de constante uit een grafiek kan halen. Dit doen ze door 1 gedeeld door x te doen. Als voorbeeld nemen ze een omgekeerd evenredig verband dus:
y=c/x >> y=c*(1/x)
Maar waarom mag dit? Hoe komen ze opeens bij die 1/x?
y = c / (x/1) -> y = c * (1/x)
Laat maar. Ik ben gekke henkie 
[ Bericht 5% gewijzigd door GoodGawd op 24-09-2012 21:37:34 (edit) ]
[ Bericht 5% gewijzigd door GoodGawd op 24-09-2012 21:37:34 (edit) ]
Blues ain't nothing but a good man feeling bad...
Volgende probleem. Bereken de volgende som:
70
(sigma) (7k - 2)
k=10
Wat ik doe: 0,5n (a1 + an)
Dus 35 (68 + 488)
35*556 = 19.460
Waar gaat dit fout?
70
(sigma) (7k - 2)
k=10
Wat ik doe: 0,5n (a1 + an)
Dus 35 (68 + 488)
35*556 = 19.460
Waar gaat dit fout?
Je moet iets verder kijken dan je neus lang is: k loopt van 10 t/m 70, dus hoeveel termen zijn er?quote:
Volgende probleem. Bereken de volgende som:
70
(sigma) (7k - 2)
k=10
Wat ik doe: 0,5n (a1 + an)
Dus 35 (68 + 488)
35*556 = 19.460
Waar gaat dit fout?
In mijn statistiekboek staat:
Variantie berekenen, een voorbeeld:
HOEZO IS DIE 4 VAN 400 WEG?!
Vertel me aub dat het een drukfout is
Variantie berekenen, een voorbeeld:
en dan nog een stukje verder..quote:s²= 441.6865 / (115-1)
= 41.6865 / 114
HOEZO IS DIE 4 VAN 400 WEG?!
Vertel me aub dat het een drukfout is
Het klopt wel wat je zegt. Maar in feite is dit gewoon de rekenregel:quote:Op maandag 24 september 2012 20:58 schreef Ron.Jeremy het volgende:
[..]
Delen door een breuk is hetzelfde als vermenigvuldigen met het omgekeerde:
y = c / (x/1) -> y = c * (1/x)
Hoe kan het volgende met de hand worden uitgerekend?
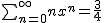
[ Bericht 50% gewijzigd door dynamiet op 25-09-2012 17:31:45 ]
[ Bericht 50% gewijzigd door dynamiet op 25-09-2012 17:31:45 ]
61quote:
[..]
Je moet iets verder kijken dan je neus lang is: k loopt van 10 t/m 70, dus hoeveel termen zijn er?
61/2 = 30,5
30,5*556 = 16.958
thanks
Dit klopt niet, want de uitdrukking in het linkerlid is afhankelijk van x en dus geen constante. Je had eerst wat anders staan. Als elke term van je reeks is op te vatten als het product van een term uit een rekenkundige reeks en een term met hetzelfde rangnummer uit een meetkundige reeks, dan heb je een zogeheten reken-meetkundige rij. Google daar maar eens op of kijk even hier (maar: er zitten nogal wat typo's in de afleiding in dit linkje. Zie ook hier).quote:
Hoe kan het volgende met de hand worden uitgerekend?
[ Bericht 0% gewijzigd door Riparius op 25-09-2012 18:40:19 ]
Idd fout van mij, dit had het moeten zijn:quote:
[..]
Dit klopt niet, want de uitdrukking in het linkerlid is afhankelijk van x en dus geen constante. Je had eerst wat anders staan. Als elke term van je reeks is op te vatten als het product van een term uit een rekenkundige reeks en een term met hetzelfde rangnummer uit een meetkundige reeks, dan heb je een zogeheten reken-meetkundige rij. Google daar maar eens op of kijk even hier (maar: er zitten nogal wat typo's de afleiding in dit linkje. Zie ook hier.
Je link lijkt erg nuttig, hier zal ik even verder mee spelen.
Het kan ook eleganter als je van differentiaalrekening en integraalrekening gebruik maakt. Stel even x in de plaats van 1/3, dan zijn de termen van je reeks van de gedaante:quote:
[..]
Idd fout van mij, dit had het moeten zijn:
Je link lijkt erg nuttig, hier zal ik even verder mee spelen.
(1) n∙xn
Dit zou je moeten doen denken aan een afgeleide, immers als we xn+1 differentiëren naar x dan krijgen we (n+1)∙xn. Dit is niet helemaal hetzelfde als n∙xn, maar we hebben wel:
(2) n∙xn = (n+1)∙xn - xn
En dus hebben we (voor |x| < 1) ook:
(3) Σ n∙xn = Σ (n+1)∙xn - Σ xn
waarbij we de som steeds nemen over n = 0..∞
Als je dus de som kunt bepalen van elk van de beide reeksen in het rechterlid van (3), dan heb je ook de som van de reeks in het linkerlid van (3). Welnu, de tweede reeks in het rechterlid van (3) is eenvoudig, want dit is een meetkundige reeks met eerste term x0 = 1 en reden x, dus hebben we:
(4) Σ xn = 1/(1-x) (|x| < 1)
Maar nu de eerste reeks in het rechterlid van (3). Als we deze termsgewijs primitiveren dan krijgen we als algemene term xn+1, want de afgeleide hiervan is immers (n+1)∙xn. Maar een reeks met als algemene term xn+1 is weer een meetkundige reeks, in dit geval met als eerste term x1 = x en weer x als reden. Dus hebben we:
(5) Σ xn+1 = x/(1-x) (|x| < 1)
En beide leden van (5) differentiëren naar x geeft dan:
(6) Σ (n+1)∙xn = 1/(1-x)2 (|x| < 1)
Dus vinden we op grond van (3), (4) en (6) dat:
(7) Σ n∙xn = 1/(1-x)2 - 1/(1-x) (|x| < 1)
En substitueren van x = 1/3 in (7) geeft dan:
(8) Σ n∙(1/3)n = 1/(2/3)2 - 1/(2/3) = 9/4 - 3/2 = 9/4 - 6/4 = 3/4
QED
[ Bericht 0% gewijzigd door Riparius op 25-09-2012 18:33:16 ]
Heel erg bedankt! Hier heb ik wat aanquote:
[..]
Het kan ook eleganter als je van differentiaalrekening en integraalrekening gebruik maakt. Stel even x in de plaats van 1/3, dan zijn de termen van je reeks van de gedaante:
(1) n∙xn
Dit zou je moeten doen denken aan een afgeleide, immers als we xn+1 differentiëren naar x dan krijgen we (n+1)∙xn. Dit is niet helemaal hetzelfde als n∙xn, maar we hebben wel:
(2) n∙xn = (n+1)∙xn - xn
En dus hebben we (voor |x| < 1) ook:
(3) Σ n∙xn = Σ (n+1)∙xn - Σ xn
waarbij we de som steeds nemen over n = 0..∞
Als je dus de som kunt bepalen van elk van de beide reeksen in het rechterlid van (3), dan heb je ook de som van de reeks in het linkerlid van (3). Welnu, de tweede reeks in het rechterlid van (3) is eenvoudig, want dit is een meetkundige reeks met eerste term x0 = 1 en reden x, dus hebben we:
(4) Σ xn = 1/(1-x) (|x| < 1)
Maar nu de eerste reeks in het rechterlid van (3). Als we deze termsgewijs primitiveren dan krijgen we als algemene term xn+1, want de afgeleide hiervan is immers (n+1)∙xn. Maar een reeks met als algemene term xn+1 is weer een meetkundige reeks, in dit geval met als eerste term x1 = x en weer x als reden. Dus hebben we:
(5) Σ xn+1 = x/(1-x) (|x| < 1)
En beide leden van (5) differentiëren naar x geeft dan:
(6) Σ (n+1)∙xn = 1/(1-x)2 (|x| < 1)
Dus vinden we op grond van (3), (4) en (6) dat:
(7) Σ n∙xn = 1/(1-x)2 - 1/(1-x) (|x| < 1)
En substitueren van x = 1/3 in (7) geeft dan:
(8) Σ n∙(1/3)n = 1/(2/3)2 - 1/(2/3) = 9/4 - 3/2 = 9/4 - 6/4 = 3/4
QED
Als e een idempotent in een commutatieve ring R is dan is (1-e) dat ook en er is een isomorfisme:
R -> R/eR X R/(1-e)R
Dit is me gelukt te bewijzen met de Chinese reststelling.
Hoe laat ik nu zien dat de idempotenten van R bijectief corresponderen met de decomposities van R als bovenstaand product?
Het lukt me niet te laten zien dat R/eR uniek is voor een idempotent e.
R -> R/eR X R/(1-e)R
Dit is me gelukt te bewijzen met de Chinese reststelling.
Hoe laat ik nu zien dat de idempotenten van R bijectief corresponderen met de decomposities van R als bovenstaand product?
Het lukt me niet te laten zien dat R/eR uniek is voor een idempotent e.
Het kan korter, bedenk ik me net. Je hebt namelijk:quote:
[..]
Heel erg bedankt! Hier heb ik wat aan
(1) Σ n∙xn = x∙Σ n∙xn-1
Welnu, we weten dat :
(2) Σ xn = 1/(1-x) (|x| < 1)
Beide leden van (2) differentiëren naar x geeft:
(3) Σ n∙xn-1 = 1/(1-x)2 (|x| < 1)
En beide leden van (3) met x vermenigvuldigen levert dus:
(4) Σ n∙xn = x/(1-x)2 (|x| < 1)
Substitutie van x = 1/3 in (4) geeft dan:
(5) Σ n∙(1/3)n = (1/3)/(2/3)2 = (1/3)∙(9/4) = 3/4
ΟΕΔ
[ Bericht 0% gewijzigd door Riparius op 27-09-2012 21:21:21 ]
iemand hier die wolfram alpha app gekocht heeft?
Is het het geld waard?
(link voor android, hij is er ook voor iOS: klik )
Is het het geld waard?
(link voor android, hij is er ook voor iOS: klik )
Winnaar KLB verkiezingen 2012.
Ik heb hem niet maar gezien de ratings is het geen miskoop. Sowieso is het maar ¤3,17. Als je de gewone wolfram alpha fijn vindt, dan zal je dat ook wel waarderen. Denk alleen dat het niet heel erg veel toevoegt t.o.v. de gewone site.quote:Op woensdag 26 september 2012 20:00 schreef gogosweden het volgende:
iemand hier die wolfram alpha app gekocht heeft?
Is het het geld waard?
(link voor android, hij is er ook voor iOS: klik )
ik zit er een beetje over in dat het met een mobiel toetsenbord natuurlijk veel kutter werken is.quote:
[..]
Ik heb hem niet maar gezien de ratings is het geen miskoop. Sowieso is het maar ¤3,17. Als je de gewone wolfram alpha fijn vindt, dan zal je dat ook wel waarderen. Denk alleen dat het niet heel erg veel toevoegt t.o.v. de gewone site.
Winnaar KLB verkiezingen 2012.
Ik moet de sample mean en covariance uitrekenen van een variabele (vector)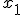 
conditioneel op twee variabelen (vectoren) 
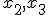met MATLAB. Er is niet genoeg bewijs om aan te nemen dat de variabelen individueel of gezamenlijk normaal verdeeld zijn. Hoe werkt dat (formule/idee, MATLAB code tikken lukt zelf nog wel)?
[ Bericht 2% gewijzigd door Physics op 27-09-2012 10:22:55 ]
[ Bericht 2% gewijzigd door Physics op 27-09-2012 10:22:55 ]
Ik heb 'm gepiraat. Geen slechte app, maar de site is beter.quote:
iemand hier die wolfram alpha app gekocht heeft?
Is het het geld waard?
(link voor android, hij is er ook voor iOS: klik )
hmm even kijken wat ik zal doen dan.quote:Op donderdag 27 september 2012 07:11 schreef Amoeba het volgende:
[..]
Ik heb 'm gepiraat. Geen slechte app, maar de site is beter.
Winnaar KLB verkiezingen 2012.
Zonder parametrisch model wordt dat lastig. Of x2/x3 moeten discreet zijn en je voor elke combinatie (x2,x3) veel waarnemingen x1 hebt.quote:
Ik moet de sample mean en covariance uitrekenen van een variabele (vector) stochastische vector
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nee ik heb een 24x3 data matrix, dus voor elk paar (x2,x3) heb ik één x1.quote:
[..]
Zonder parametrisch model wordt dat lastig. Of x2/x3 moeten discreet zijn en je voor elke combinatie (x2,x3) veel waarnemingen x1 hebt.
Oh, de stochasten zijn niet vectorwaardig. Dan vraag ik me af over wat voor covariantie je het hebt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Het blijkt nogal een vage vraag te zijn. Uit q-q plots en chi-squared plots is er geen bewijs voor normaliteit, integendeel. En dan in de laatste vraag moeten we opeens de assumptie doen (staat niet bij de opgave) dat de data multivariaat normaal verdeeld is.
Hoe bedoel je dat de stochasten niet vectorwaardig zijn?
Hoe bedoel je dat de stochasten niet vectorwaardig zijn?
Je stochast is univariaat, en je vector bestaat uit waarnemingen.quote:
Hoe bedoel je dat de stochasten niet vectorwaardig zijn?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dat klopt, en hoezo zou er dan geen covariantie kunnen zijn tussen de stochasten?quote:
[..]
Je stochast is univariaat, en je vector bestaat uit waarnemingen.
Je had het over "gegeven x_2, x_3", en dan is de covariantie 0 want dan zijn x_2 en x_3 constanten.quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Weet iemand een goed boek over functionaalanalyse?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Ik heb een vraag over verzamelingenleer en dan in het bijzonder over relaties tussen verzamelingen:
Wanneer is er nou sprake van een transitieve relatie? En geldt deze relatie ook voor een relatie met daarin slechts één element. Wat ik begrepen heb is dat voor een transitieve relatie altijd geldt:<a, b>, <b, c> en dus <c, a>, maar iemand merkte op dat een enkele element (dus bijvoorbeeld <a, b>) ook transitief is.
Wanneer is er nou sprake van een transitieve relatie? En geldt deze relatie ook voor een relatie met daarin slechts één element. Wat ik begrepen heb is dat voor een transitieve relatie altijd geldt:<a, b>, <b, c> en dus <c, a>, maar iemand merkte op dat een enkele element (dus bijvoorbeeld <a, b>) ook transitief is.
Kom maar konijntje, doe maar wiebelen wiebelen...
Misschien moet je de vraag opnieuw stellen zodra je weer nuchter bent, want hier is geen chocola van te maken.quote:
Ik heb een vraag over verzamelingenleer en dan in het bijzonder over relaties tussen verzamelingen:
Wanneer is er nou sprake van een transitieve relatie? En geldt deze relatie ook voor een relatie met daarin slechts één element. Wat ik begrepen heb is dat voor een transitieve relatie altijd geldt:<a, b>, <b, c> en dus <c, a>, maar iemand merkte op dat een enkele element (dus bijvoorbeeld <a, b>) ook transitief is.
Mijn vraag is: wanneer is er sprake van transitiviteit? En hoe zit het met een relatie R als er maar één relatie in zit, dus {<a, b>}. Want ik heb begrepen dat bij transitiviteit een driehoeksrelatie speelt, maar dat is blijkbaar niet het enige.quote:
[..]
Misschien moet je de vraag opnieuw stellen zodra je weer nuchter bent, want hier is geen chocola van te maken.
Kom maar konijntje, doe maar wiebelen wiebelen...
Je vraag blijft vaag. Transitiviteit heb je als aRb en bRc impliceert aRc voor alle elementen a,b,c, waarbij R een relatie is.
Wat is een driehoeksrelatie? Behalve dan drie mensen die een relatie met elkaar hebben. Wat bedoel je met dat er één element in een relatie zit?
Geef anders eens een voorbeeld.
Wat is een driehoeksrelatie? Behalve dan drie mensen die een relatie met elkaar hebben. Wat bedoel je met dat er één element in een relatie zit?
Geef anders eens een voorbeeld.
In de voorwaarde "als aRb en bRc, dan ook aRc" hoeven a, b, en c niet verschillend te zijn. Is dat wat je met je vraag bedoelt?
Als er één element in je verzameling zit, en dat element heeft een relatie met zichzelf, dan is er sprake van transitiviteit. Want aRb, bRc, aRc worden dan allemaal aRa. En uiteraard:
aRa en aRa ==> aRa.
aRa en aRa ==> aRa.
Maar als er nou alleen aRb in een relatie zit, dan is er geen sprake van transitiviteit? (Misschien heb ik het niet helemaal goed begrepen hoor.)quote:
Als er één element in je verzameling zit, en dat element heeft een relatie met zichzelf, dan is er sprake van transitiviteit. Want aRb, bRc, aRc worden dan allemaal aRa. En uiteraard:
aRa en aRa ==> aRa.
Misschien maak ik trouwens een denkfout... Is het zo dan een relatie per definitie op alle elementen in een verzameling slaat? Dus niet dat het slechts enkele elementen heeft?
Kom maar konijntje, doe maar wiebelen wiebelen...
Een relatie slaat op elk paar elementen van de verzameling, en voor elk paar kan de relatie wel of niet gelden. Simpel voorbeeld: neem de verzameling van reële getallen, met als relatie "<" (a is kleiner dan b). Voor elk paar getallen a en b kun je zeggen of a<b wel of niet geldt, zo geldt 1<2 wel, maar 4<3 geldt niet, etc.
Precies. Dus "aRb zit in een relatie" is nogal vaag. Je zegt ook niet: 1<2 zit in een relatie.
Misschien bedoel je dat de relatie aRb slechts voor twee verschillende elementen a en b geldt. Bijvoorbeeld:
Stel je hebt de verzameling X={1,2} en als relatie R heb je <. Dan geldt dus alleen 1<2 (niet 1<1, 2<1, 2<2). Als je wil checken op transitiviteit (dus: a<b en b<c ==> a<c), dan zie je dat je de premisse van de implicatie niet waar kan maken.
Een regel uit de logica is dat "A==>B" waar is als A niet waar is. Dus inderdaad heb je in dit voorbeeld transitiviteit. (en dit verhaal kan je ook weer algemeen maken)
Is dat wat je bedoelt?
[ Bericht 37% gewijzigd door thenxero op 29-09-2012 16:03:24 ]
Misschien bedoel je dat de relatie aRb slechts voor twee verschillende elementen a en b geldt. Bijvoorbeeld:
Stel je hebt de verzameling X={1,2} en als relatie R heb je <. Dan geldt dus alleen 1<2 (niet 1<1, 2<1, 2<2). Als je wil checken op transitiviteit (dus: a<b en b<c ==> a<c), dan zie je dat je de premisse van de implicatie niet waar kan maken.
Een regel uit de logica is dat "A==>B" waar is als A niet waar is. Dus inderdaad heb je in dit voorbeeld transitiviteit. (en dit verhaal kan je ook weer algemeen maken)
Is dat wat je bedoelt?
[ Bericht 37% gewijzigd door thenxero op 29-09-2012 16:03:24 ]
Stond hier gister niet een puzzel met 4 van die sterretjes erin? Repost? :p I like puzzles.
Blues ain't nothing but a good man feeling bad...
Daar stond de puzzel, maar hij is inmiddels weggehaald: [Bèta overig] Huiswerk- en vragentopicquote:
Stond hier gister niet een puzzel met 4 van die sterretjes erin? Repost? :p I like puzzles.
Volgens mij was het een 8*8 raster met 4 sterretjes op de diagonaal van linksboven naar rechtsonder. Ik meen dat de opdracht was om het raster in vier gelijkvormige delen op te delen, zodanig dat in elk deel een ster voorkwam en alle delen elkaar raakten.
Voor iedereen die er belang in stelt: ik heb mijn post met het elementaire bewijs met vectoren van de somformules voor cos(α + β) en sin(α + β) bewerkt tot een PDF die hier is te bekijken en desgewenst is te downloaden. Met dank aan Amoeba voor het vervaardigen van het plaatje.
Kan iemand mij misschien helpen met het volgende?
Schrijf als een exponentiele functie met grondtel e de groei van ¤3000 tegen 5% rente per jaar.
Nu is de groei dus y = 3000 * 1,05x
Maar het grondgetal moet e zijn, hoe krijg ik dat ingodsnaam voor elkaar
Schrijf als een exponentiele functie met grondtel e de groei van ¤3000 tegen 5% rente per jaar.
Nu is de groei dus y = 3000 * 1,05x
Maar het grondgetal moet e zijn, hoe krijg ik dat ingodsnaam voor elkaar
Als je dus bedenkt dat ep gelijk is aan je functie, waarbij p een uitdrukking is in x. Lukt het dan?
En bedenk dat:
3000 = eln(3000)
The way to go.
[ Bericht 45% gewijzigd door #ANONIEM op 02-10-2012 19:13:11 ]
En bedenk dat:
3000 = eln(3000)
The way to go.
[ Bericht 45% gewijzigd door #ANONIEM op 02-10-2012 19:13:11 ]
Waarom had ik die ep nodig?
Ik heb nu dit
y = 3000 * 1,05x
ep = eln3000 * eln1,05x
y = eln3000 + ln(1,05x)
y = eln(3150x)
Ik heb nu dit
y = 3000 * 1,05x
ep = eln3000 * eln1,05x
y = eln3000 + ln(1,05x)
y = eln(3150x)
Je tweede regel is in feite niet goed. Het is niet ln(1.05x)
Je moet begrijpen dat je in feite een uitdrukking krijgt waarbij e het grondtal is, en waarbij p een uitdrukking is in x. Als je e tot de macht p verheft krijg je dus in feite y.
Je wilt y omschrijven naar een vorm ep
[ Bericht 68% gewijzigd door #ANONIEM op 02-10-2012 19:29:06 ]
Je moet begrijpen dat je in feite een uitdrukking krijgt waarbij e het grondtal is, en waarbij p een uitdrukking is in x. Als je e tot de macht p verheft krijg je dus in feite y.
Je wilt y omschrijven naar een vorm ep
[ Bericht 68% gewijzigd door #ANONIEM op 02-10-2012 19:29:06 ]
e ln (1,05)x = eln1,05x toch?quote:
Je tweede regel is in feite niet goed. Het is niet ln(1.05x)
Je hebt uiteraard:quote:
Kan iemand mij misschien helpen met het volgende?
Schrijf als een exponentiele functie met grondtel e de groei van ¤3000 tegen 5% rente per jaar.
Nu is de groei dus y = 3000 * 1,05x
Maar het grondgetal moet e zijn, hoe krijg ik dat ingodsnaam voor elkaar
1,05 = eln(1,05)
Verder kun je gebruik maken van de rekenregel:
(ap)q = apq
Wat krijg je dan?
Je zou ook nog kunnen zeggen dat
3000 = eln(3000)
Dan kun je daarna nog gebruik maken van de rekenregel:
ap∙aq = ap+q
Wat krijg je dan?
Correct. (als ik me niet vergisquote:
[..]
Ohja, dat maakt dus
y = e ln(3150) * x ?
)[ Bericht 1% gewijzigd door #ANONIEM op 02-10-2012 20:09:07 ]
Nee.quote:
[..]
Ohja, dat maakt dus
y = e ln(3150) * x ?
Jawel. Bij (eln(1.05))x = eln(1.05)xquote:
Dan is de regel (ap)q = apq toch niet gebruikt?
[ Bericht 3% gewijzigd door #ANONIEM op 02-10-2012 19:48:07 ]
Daar gebruik je toch log(ab) = b*log(a) ?quote:
[..]
Jawel. Bij e^ln(1.05)^x = e^ln(1.05)x
Nee.quote:
[..]
Daar gebruik je toch log(ab) = b*log(a) ?
Ik zal je maar even uit je lijden verlossen, want dit wordt een gebed zonder end. Ik verbaas me iedere dag meer over het volstrekte gebrek aan basale wiskundekennis bij mensen die vervolgopleidingen gaan doen waar je die kennis gewoon nodig hebt, maar goed dat is een andere discussie (Bram, kom er maar in ...).quote:
Je hebt:
y = 3000∙1,05x = 3000∙(eln(1,05))x = 3000∙ex∙ln(1,05) = eln(3000)∙ex∙ln(1,05) = eln(3000)+x∙ln(1,05).
That's all.
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |