SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Oke de integraal klopt dus. Maar dan hoe reken ik deze uit? Wolfram geeft http://www.wolframalpha.com/input/?i=int+sqrt%281+%2B+4*t%29+*+sqrt%281+%2B+1%2F%284*t%29%29+dt maar daar begrijp ik de stap niet van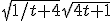 
naar 
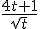niet. De integraal moet simpeler op te lossen zijn toch ook trouwens?
Het is beter om gebruik te maken van:quote:Op maandag 25 juni 2012 22:30 schreef thenxero het volgende:
[..]
Wolfram alpha geeft geen exact antwoord (dus die zal niet bestaan of vrij gecompliceerd zijn), dus je zult het dan moeten benaderen net zoals je rekenmachine dat doet. Je kan hiervoor een Taylorreeks gebruiken... die van de arctan convergeert heel snel dus na een aantal termen ben je wel klaar (vooral als x dichtbij 0 zit).
Die snelle benadering geeft al arctan(3/4) = 0.656 terwijl het eigenlijk 0.643 is.
Sommige waarden kan je wel makkelijk exact berekenen, zoals arctan(1) of arctan(0) (probeer maar).
arctan(3/4) = 2∙arctan(1/3)
aangezien de reeks (zoals je zelf opmerkt) sneller convergeert naarmate x dichter bij 0 ligt.
Dan krijg je:
arctan(3/4) ≈ 2∙(1/3 - (1/3)3/3 + (1/3)5/5) = 782/1215 = 0,6436 ...
Nog veel beter wordt het als je gebruik maakt van
arctan(3/4) = π/4 - arctan(1/7)
Aangezien we niet eerst een benadering voor π uit willen rekenen (waarvoor we ook weer een reeksontwikkeling nodig zouden hebben) maken we hiervoor gebruik van de benadering 355/113 (het getal van Metius). Dan krijgen we:
arctan(3/4) ≈ (1/4)∙(355/113) - (1/7 - (1/7)3/3 + (1/7)5/5) = 0,643501...
En zie daar, we hebben arctan(3/4) in zes decimalen nauwkeurig.
[ Bericht 15% gewijzigd door Riparius op 26-06-2012 03:32:50 ]
Je moet niet meteen je probleem in WolframAlpha (of een ander computeralgebra systeem) stoppen en dan proberen dat slaafs na te doen met pen en papier. Een mens is nog altijd creatiever dan een computer (maar jij kennelijk niet ...).quote:Op dinsdag 26 juni 2012 00:45 schreef Dale. het volgende:
Oke de integraal klopt dus. Maar dan hoe reken ik deze uit? Wolfram geeft http://www.wolframalpha.com/input/?i=int+sqrt%281+%2B+4*t%29+*+sqrt%281+%2B+1%2F%284*t%29%29+dt maar daar begrijp ik de stap niet van
Ik ga eerst je integrand in een wat hanteerbaarder vorm brengen. We hebben:
√(1 + 4t)∙√(1 + 1/(4t)) = √(1 + 1/(4t) + 4t + 1) = √(4t + 2 + 1/(4t))
Nu gaan we de termen onder het wortelteken onder één noemer brengen. Dit geeft:
4t + 2 + 1/(4t) = (16t2 + 8t + 1)/(4t) = (4t + 1)2/(4t)
Dus krijgen we:
√(4t + 2 + 1/(4t)) = (4t + 1)∙(4t)-1/2 = ½∙(4t + 1)∙t-1/2 = 2∙t1/2 + ½∙t-1/2
De integraal wordt nu:
∫01 (2∙t1/2 + ½∙t-1/2)∙dt = [(4/3)∙t3/2 + t1/2]01 = 4/3 + 1 = 7/3.
[ Bericht 0% gewijzigd door Riparius op 26-06-2012 02:33:30 ]
Volgens mij zou het rekenmachine het ook niet eens zijn met arccos(-arctan(3/4)), dus, ja, het moest inderdaad cos zijn. Foutje.quote:
[..]
Weet je zeker dat er niet naar cos(-arctan(3/4)) wordt gevraagd?
"Social order at the expense of liberty is hardly a bargain."
Je begrijpt er kennelijk nog niet veel van, want -arctan(3/4) ligt tussen -π/4 en 0 en daarmee binnen het domein [-1,1] van de (reële) arcus cosinus functie, zodat arccos(-arctan(3/4)) gewoon (numeriek) is te bepalen.quote:Op dinsdag 26 juni 2012 11:50 schreef Quir het volgende:
[..]
Volgens mij zou de rekenmachine het ook niet eens zijn met arccos(-arctan(3/4)), dus, ja, het moest inderdaad cos zijn. Foutje.
Maar goed, het ging dus om cos(-arctan(3/4)).
Laten we zeggen dat
arctan(3/4) = α,
dan is
tan α = 3/4, met -½π < α < ½π
Nu maken we gebruik van de identiteit
1 + tan2α = sec2α,
waarvoor we uiteraard ook kunnen schrijven
1 + tan2α = 1/cos2α
We weten dat tan α = 3/4, dus hebben we
1/cos2α = 1 + (3/4)2 = 25/16,
en dus
cos2α = 16/25
Nu hebben we ook -½π < α < ½π en dus is cos α > 0, zodat we vinden
cos α = 4/5
De cosinusfunctie is een even functie, en dus is ook
cos(-α) = 4/5
En aangezien arctan(3/4) = α heb je dus:
cos(-arctan(3/4)) = cos(-α) = 4/5.
Voila.
Je zou ook een plaatje kunnen tekenen, en dan zie je dat je te maken hebt met een rechthoekige driehoek waarvan de zijden zich verhouden als 3 : 4 : 5 aangezien tan α = 3/4 gelijk is aan de overstaande rechthoekszijde gedeeld door de aanliggende rechthoekszijde van hoek α. En aangezien de cosinus van deze hoek gelijk is aan de aanliggende rechthoekszijde gedeeld door de schuine zijde, weet je dan direct dat cos α = 4/5.
[ Bericht 5% gewijzigd door Riparius op 26-06-2012 14:02:15 ]
Pagina 149 zegt [0, pi] en daar ligt -arctan(3/4) voor zover ik weet niet in. Als ik danwel 't boek iets fout heeft hoor ik het graag.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt."Social order at the expense of liberty is hardly a bargain."
En ohja, sec ben ik nog niet tegengekomen in 't boek, maar de rest wel. Ik volg het verder, dank!
"Social order at the expense of liberty is hardly a bargain."
quote:Op dinsdag 26 juni 2012 12:35 schreef Quir het volgende:
Pagina 149 zegt [0, pi] en daar ligt -arctan(3/4) voor zover ik weet niet in. Als ik danwel 't boek iets fout heeft hoor ik het graag.Nee, je begrijpt het niet. Het pleit ook niet voor je dat je kennelijk meer vertrouwen hebt in een - foutief - gebruik van je rekenmachine dan in mijn uitleg. Ik vermoed dat je je rekenmachine op graden hebt laten staan in plaats van op radialen, en dan is het nogal wiedes dat de machine je invoer niet accepteert. Dit is weer typisch zo'n hersenloos gebruik van een calculator.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Je hebt -½π < arctan(x) < ½π voor elke reële x, en arctan(0) = 0 en arctan(1) = ¼π. De arcus tangens functie is strict monotoon stijgend zodat arctan(0) < arctan(¾) < arctan(1) en dus 0 < arctan(¾) < ¼π en dus -¼π < -arctan(¾) < 0. En aangezien 0 < π < 4 is dus -1 < -¼π < 0 en daarmee -1 < -arctan(¾) < 0.
[ Bericht 14% gewijzigd door Riparius op 26-06-2012 14:56:31 ]
Ik had dus een paar uur geleden m'n wiskunde mondeling.
1. casus, wat eenvoudige goniometrie, raaklijnen en integralen. Op her en der een haakje en een k*2π na foutloos.
2. meetkunde: totaal verneukt (zoals iedereen)
3. wentelen, piece of cake.,
3. logaritmen. peanuts
4. optimaliseren, slordig begonnen, na een vermaning foutloos.
5. Mijn klok! Kreeg wat historische vragen(hij gaf toe dat mijn kennis van de wiskundige historie verder was dan de zijne)
6. Mercatorprojectie. Hij was onder de indruk, ondanks de geringe hoeveelheid tijd kreeg ik toch nog een vraag over poolcoördinaten. Mijn werkstuk is daarna ingenomen voor nadere observatie (hij wilde wel even kijken wat ik van deze 'hogere' wiskunde bakte.
Rip, bedankt!
1. casus, wat eenvoudige goniometrie, raaklijnen en integralen. Op her en der een haakje en een k*2π na foutloos.
2. meetkunde: totaal verneukt (zoals iedereen)
3. wentelen, piece of cake.,
3. logaritmen. peanuts
4. optimaliseren, slordig begonnen, na een vermaning foutloos.
5. Mijn klok! Kreeg wat historische vragen(hij gaf toe dat mijn kennis van de wiskundige historie verder was dan de zijne)
6. Mercatorprojectie. Hij was onder de indruk, ondanks de geringe hoeveelheid tijd kreeg ik toch nog een vraag over poolcoördinaten. Mijn werkstuk is daarna ingenomen voor nadere observatie (hij wilde wel even kijken wat ik van deze 'hogere' wiskunde bakte.
Rip, bedankt!
Graag gedaan. Maar wat hielden die meetkunde opgaven in?quote:
Ik had dus een paar uur geleden m'n wiskunde mondeling.
1. casus, wat eenvoudige goniometrie, raaklijnen en integralen. Op her en der een haakje en een k*2π na foutloos.
2. meetkunde: totaal verneukt (zoals iedereen)
3. wentelen, piece of cake.,
3. logaritmen. peanuts
4. optimaliseren, slordig begonnen, na een vermaning foutloos.
5. Mijn klok! Kreeg wat historische vragen(hij gaf toe dat mijn kennis van de wiskundige historie verder was dan de zijne)
6. Mercatorprojectie. Hij was onder de indruk, ondanks de geringe hoeveelheid tijd kreeg ik toch nog een vraag over poolcoördinaten. Mijn werkstuk is daarna ingenomen voor nadere observatie (hij wilde wel even kijken wat ik van deze 'hogere' wiskunde bakte.
Rip, bedankt!
Helder!quote:
[..]
Nee, je begrijpt het niet. Het pleit ook niet voor je dat je kennelijk meer vertrouwen hebt in een - foutief - gebruik van je rekenmachine dan in mijn uitleg. Ik vermoed dat je je rekenmachine op graden hebt laten staan in plaats van op radialen, en dan is het nogal wiedes dat de machine je invoer niet accepteert. Dit is weer typisch zo'n hersenloos gebruik van een calculator.
Je hebt -½π < arctan(x) < ½π voor elke reële x, en arctan(0) = 0 en arctan(1) = ¼π. De arcus tangens functie is strict monotoon stijgend zodat arctan(0) < arctan(¾) < arctan(1) en dus 0 < arctan(¾) < ¼π en dus -¼π < -arctan(¾) < 0. En aangezien 0 < π < 4 is dus -1 < -¼π < 0 en daarmee -1 < -arctan(¾) < 0.
[ afbeelding ]
"Social order at the expense of liberty is hardly a bargain."
Oh, ik zie dat er in de tussentijd tekst is toegevoegd in de quote.
"Social order at the expense of liberty is hardly a bargain."
Je bent wel een botte zak af en toe, weet je. Ik heb het niet ingevoerd op mijn rekenmachine, ik had de uitkomst van de arctan gewoon verkeerd ingeschat. Ik leer, ik leer.
"Social order at the expense of liberty is hardly a bargain."
De omschreven cirkel, dat lukte nog. Ik zal straks even een schetsje maken. (oppervlakte van maantjes)
Je verwijst in je spoiler naar 't rekenmachien kennelijk in een poging om je gelijk te halen. Ik kon dus niets anders dan concluderen dat je had geprobeerd met je rekenmachine arccos(-arctan(3/4)) te bepalen en dat dat niet was gelukt omdat je machine een foutmelding gaf.quote:
Je bent wel een botte zak af en toe, weet je. Ik heb het niet ingevoerd op mijn rekenmachine, ik had de uitkomst van de arctan gewoon verkeerd ingeschat. Ik leer, ik leer.
Maar als je het goed doet vind je (met de calculator van Windows) gewoon dat arccos(-arctan(3/4)) = 2,2698597989145314710273704204042 ...
Neen, ik wou m'n keuze voor 'het' in plaats van 'de' rechtvaardigen.
"Social order at the expense of liberty is hardly a bargain."
Wees blij dat die 'botte zak' je wil helpen.quote:
Je bent wel een botte zak af en toe, weet je. Ik heb het niet ingevoerd op mijn rekenmachine, ik had de uitkomst van de arctan gewoon verkeerd ingeschat. Ik leer, ik leer.
Nou, zoals beloofd nog even die meetkunde opgave. Ik had een rechthoekige driehoek, met zijde a en b, de hypotenusa was dus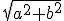 
Goed, ik had de 2 omschreven cirkels van a en b al, dus met het middelpunt op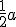
en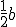 
Het midden van beide zijdes was ook gemarkeerd, en dat was mijn eerste fout, ik ging daar zoeken. Ik moest het middelpunt van de omschreven cirkel aanwijzen. Nou, ik dus eerst beginnen met een faaltekening van de zwaartelijnen, en vervolgens kwam ik wel tot een goede constructie (met een kleine afwijking) door de middelloodlijnen te construeren. Pas toen hij zei het ligt op die zijde, maar WAAROM? ging ik met de stelling van Thales roepen. (Ja zo stom dat ik het niet eerder zag, ik kon me wel voor m'n kop slaan.) Maargoed, uiteindelijk kwam het er.
En ik had daar zoveel moeite mee, het liep niet, ik werd zenuwachtig, hij ging maar door. Hij kraste op de tekening (ik heb hem even geschetst) 2 stukjes in.
Nu moest ik aantonen dat de som van deze 2 stukjes gelijk was aan de oppervlakte van de driehoek. Toen vroeg hij me naar de oppervlakte van een cirkel, ik half verdwaasd zet er 2 pi * r neer, hij kijkt me aan, ik kijk nog eens, verander het r^2 maar liet de 2 staan. Echt, ik had het niet meer. Hij moest dus gewoon zeggen dat het pi r^2 was, maar dat terzijde.
Uiteindelijk had ik de formules van elke halve cirkel, maar ik kwam er niet tot, toen liet hij het maar zitten. Tot zover meetkunde, toen kwam het wentelen om de x-as en daar begon de pret. Ik zei ook maar gewoon eerlijk dat meetkunde een 4,8 was en me totaal niet lag, toen vroeg hij of e-machten me wel lagen, nou verder mocht hij losvragen wat hij wilde, alleen tijdens het optimaliseren ging ik eventjes mezelf voorbij en moest hij me tot rust manen vooraleer ik de opgave uit kon werken.
Ik had hem naderhand nog even gesproken over dat werkstuk, hij snapte het punt over de differentiaalvergelijking niet helemaal, hoe ik vanuit daar tot de integraal kwam. (De dy/dx en de integraal zijn toch 'inverse bewerkingen'?)
Maar verder wel voor al m'n examens dit jaar geslaagd (weet ik vrij zeker), Kreeg ik nog een of ander gesprek a.d.h.v. een ruzietje gisteren (nouja, 'ruzie', vechtpartij) met een jongen waarbij hij (en daarna ik) flink door het lint ging. Nu moet ik voor al m'n vrije uren (want daar schuilt mijn zwakte, ik kan daar niet goed mee omgaan als er geen opgave voor m'n neus ligt) een invulling zoeken met de stagebegeleider, dus bij Philips of ASML een stage lopen ofzo, anders kan ik het volgend jaar vergeten en bij de LOI beginnen. Leuk einde van het schooljaar.. Weet jij toevallig of je met 6 vwo wiskunde B en 4-5 vwo wiskunde D (ga ik volgend jaar dus afronden) daar iets te zoeken hebt?
[ Bericht 12% gewijzigd door #ANONIEM op 26-06-2012 19:06:20 ]
Goed, ik had de 2 omschreven cirkels van a en b al, dus met het middelpunt op
Het midden van beide zijdes was ook gemarkeerd, en dat was mijn eerste fout, ik ging daar zoeken. Ik moest het middelpunt van de omschreven cirkel aanwijzen. Nou, ik dus eerst beginnen met een faaltekening van de zwaartelijnen, en vervolgens kwam ik wel tot een goede constructie (met een kleine afwijking) door de middelloodlijnen te construeren. Pas toen hij zei het ligt op die zijde, maar WAAROM? ging ik met de stelling van Thales roepen. (Ja zo stom dat ik het niet eerder zag, ik kon me wel voor m'n kop slaan.) Maargoed, uiteindelijk kwam het er.
En ik had daar zoveel moeite mee, het liep niet, ik werd zenuwachtig, hij ging maar door. Hij kraste op de tekening (ik heb hem even geschetst) 2 stukjes in.
Nu moest ik aantonen dat de som van deze 2 stukjes gelijk was aan de oppervlakte van de driehoek. Toen vroeg hij me naar de oppervlakte van een cirkel, ik half verdwaasd zet er 2 pi * r neer, hij kijkt me aan, ik kijk nog eens, verander het r^2 maar liet de 2 staan. Echt, ik had het niet meer. Hij moest dus gewoon zeggen dat het pi r^2 was, maar dat terzijde.
Uiteindelijk had ik de formules van elke halve cirkel, maar ik kwam er niet tot, toen liet hij het maar zitten. Tot zover meetkunde, toen kwam het wentelen om de x-as en daar begon de pret. Ik zei ook maar gewoon eerlijk dat meetkunde een 4,8 was en me totaal niet lag, toen vroeg hij of e-machten me wel lagen, nou verder mocht hij losvragen wat hij wilde, alleen tijdens het optimaliseren ging ik eventjes mezelf voorbij en moest hij me tot rust manen vooraleer ik de opgave uit kon werken.
Ik had hem naderhand nog even gesproken over dat werkstuk, hij snapte het punt over de differentiaalvergelijking niet helemaal, hoe ik vanuit daar tot de integraal kwam. (De dy/dx en de integraal zijn toch 'inverse bewerkingen'?)
Maar verder wel voor al m'n examens dit jaar geslaagd (weet ik vrij zeker), Kreeg ik nog een of ander gesprek a.d.h.v. een ruzietje gisteren (nouja, 'ruzie', vechtpartij) met een jongen waarbij hij (en daarna ik) flink door het lint ging. Nu moet ik voor al m'n vrije uren (want daar schuilt mijn zwakte, ik kan daar niet goed mee omgaan als er geen opgave voor m'n neus ligt) een invulling zoeken met de stagebegeleider, dus bij Philips of ASML een stage lopen ofzo, anders kan ik het volgend jaar vergeten en bij de LOI beginnen. Leuk einde van het schooljaar.. Weet jij toevallig of je met 6 vwo wiskunde B en 4-5 vwo wiskunde D (ga ik volgend jaar dus afronden) daar iets te zoeken hebt?
[ Bericht 12% gewijzigd door #ANONIEM op 26-06-2012 19:06:20 ]
Wat bijzonder om een mondeling wiskunde-examen te hebben. Lijkt me veel rechtvaardiger, want je weet in een halve minuut of iemand bluft, terwijl je dat op papier van het beste moet uitgaan.
Oppervlakte van de hele figuur is
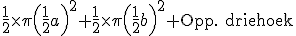
(halve cirkel op zijde a plus halve cirkel op zijde b plus driehoek)
Oppervlakte van de omgeschreven halve cirkel is
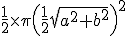
Eerste van tweede oppervlakte aftrekken en je houdt opp. driehoek over.
Oppervlakte van de hele figuur is
(halve cirkel op zijde a plus halve cirkel op zijde b plus driehoek)
Oppervlakte van de omgeschreven halve cirkel is
Eerste van tweede oppervlakte aftrekken en je houdt opp. driehoek over.
Je kunt met behulp van Pythagoras meteen (zonder rekenwerk) de conclusie trekken dat de oppervlakte van de gearceerde vlakdelen samen gelijk moet zijn aan de oppervlakte van de driehoek, zijnde ½ab. De beide halve cirkels op de rechthoekszijden hebben immers samen een oppervlakte die gelijk is aan de oppervlakte van de halve cirkel op de hypotenusa.quote:
Wat bijzonder om een mondeling wiskunde-examen te hebben. Lijkt me veel rechtvaardiger, want je weet in een halve minuut of iemand bluft, terwijl je dat op papier van het beste moet uitgaan.
Oppervlakte van de hele figuur is
(halve cirkel op zijde a plus halve cirkel op zijde b plus driehoek)
Oppervlakte van de omgeschreven halve cirkel is
Eerste van tweede oppervlakte aftrekken en je houdt opp. driehoek over.
Ik heb het ook absoluut niet op mondelinge tentamens. Er is ook geen enkele garantie op objectiviteit bij de beoordeling, en controle achteraf is niet mogelijk.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Is maar net bij wie je het afneemt. Soms kan je op een mondeling net een duwtje in de goede richting krijgen. Maar doe mij ook maar gewoon schriftelijkquote:
Mondeling is veel lastiger dan schriftelijk. Je wordt echt opgejaagd soms.
het duwtje kan ook de andere kant op zijn, ik kreeg een keer 3 punten onder het gemiddelde van mijn andere vakkenquote:
[..]
Is maar net bij wie je het afneemt. Soms kan je op een mondeling net een duwtje in de goede richting krijgen. Maar doe mij ook maar gewoon schriftelijk
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Tsjah, wiskunde verliep eerlijk, scheikunde in mijn voordeel. Hij hield snel genoeg op met meetkunde en gaf me de kans om te knallen bij logaritmen. Ik kreeg alleen geen kans om aan die Mercatorprojectie te beginnen.
Ik zou er bloedzenuwachtig van worden. Als je iets niet snapt bij een schriftelijk examen kan je het even laten liggen en daarna verder gaan, maar zo'n opgave als die je net liet zien zou ik denk ik niks van bakken bij een mondelinge overhoring, en volgens mij niet veel vwo-leerlingen (je zei ook al dat iedereen het had verneukt, niet verwonderlijk).quote:
Mondeling is veel lastiger dan schriftelijk. Je wordt echt opgejaagd soms.
Als ik die opgave hier nu had liggen en ik moest hem maken was me dat wel gelukt. Even rustig voor gaan zitten en gaan.
Maar je bént ook bloedzenuwachtig. Het mondeling examen telt net zo hard mee als het schriftelijk, dat maakt het een godverdomd belangrijk punt.
Ik krijg morgen te horen wat ik schriftelijk en mondeling gedaan heb, ofwel de uitslag.
Maar je bént ook bloedzenuwachtig. Het mondeling examen telt net zo hard mee als het schriftelijk, dat maakt het een godverdomd belangrijk punt.
Ik krijg morgen te horen wat ik schriftelijk en mondeling gedaan heb, ofwel de uitslag.
Nog een vraagje...
Als er staat... "Determine the area A of that portion of the paraboloid, x^2 + y^2 + z = 9, where x >= 0, y >= 0 and z >= 0."
Wordt er nu gevraagd naar de oppervlakte integraal?
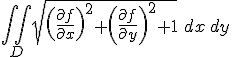
Als er staat... "Determine the area A of that portion of the paraboloid, x^2 + y^2 + z = 9, where x >= 0, y >= 0 and z >= 0."
Wordt er nu gevraagd naar de oppervlakte integraal?
Ik denk niet dat ze willen dat je een volume uitrekent, jij wel?quote:
Nog een vraagje...
Als er staat... "Determine the area A of that portion of the paraboloid, x^2 + y^2 + z = 9, where x >= 0, y >= 0 and z >= 0."
Wordt er nu gevraagd naar de oppervlakte integraal?
Begin dit maar eens goed door te nemen.quote:
Nee maar dat bereken je toch ook niet met een oppervlakte integraal? Je berekent daarmee het oppervlak van de vorm. Dus ja ik geloof dat ik gewoon correct zit. Ik zit er vooral over te duppen dat ik de vraagstelling niet snap, wat komt omdat ik op mijn aantekening een schets heb van de vorm waarbij ik het gebied dat op het x-y-vlak wordt geprojecteerd door de paraboloïde heb gearceerd en area heb bijgeschreven, mijn aantekening is vast goed bedoeld maar verkeerd opgeschrevenquote:
[..]
Ik denk niet dat ze willen dat je een volume uitrekent, jij wel?
[..]
Begin dit maar eens goed door te nemen.
Gevraagd wordt de oppervlakte van een deel van de paraboloïde te berekenen. En je hebt daarvoor de juiste integraal. Maar nu moet je nog bepalen wat D voorstelt. Dat is inderdaad de projectie van het deel van de paraboloïde waarvan je de oppervlakte moet bepalen op het xy-vlak. Het is niet de bedoeling dat je de oppervlakte van D bepaalt, dat is een kwart van een cirkel met straal 3. Maar D is het gebied in het xy-vlak waarover je integreert.quote:
[..]
Nee maar dat bereken je toch ook niet met een oppervlakte integraal? Je berekent daarmee het oppervlak van de vorm. Dus ja ik geloof dat ik gewoon correct zit. Ik zit er vooral over te dubben dat ik de vraagstelling niet snap, wat komt omdat ik op mijn aantekening een schets heb van de vorm waarbij ik het gebied dat op het x-y-vlak wordt geprojecteerd door de paraboloïde heb gearceerd en area heb bijgeschreven, mijn aantekening is vast goed bedoeld maar verkeerd opgeschreven
Thanks! Had D al bepaald, wist alleen niet of ik nu wel gewoon het juiste berekend heb. Je krijgt namelijk dan de integraal:quote:
[..]
Gevraagd wordt de oppervlakte van een deel van de paraboloïde te berekenen. En je hebt daarvoor de juiste integraal. Maar nu moet je nog bepalen wat D voorstelt. Dat is inderdaad de projectie van het deel van de paraboloïde waarvan je de oppervlakte moet bepalen op het xy-vlak. Het is niet de bedoeling dat je de oppervlakte van D bepaalt, dat is een kwart van een cirkel met straal 3. Maar D is het gebied in het xy-vlak waarover je integreert.
Er komt zo te zien toch iets anders uit.quote:
[..]
Thanks! Had D al bepaald, wist alleen niet of ik nu wel gewoon het juiste berekend heb. Je krijgt namelijk dan de integraal:
Je hebt kennelijk na de substitutie u = 1 + 4r2, du = 8rdr de verkeerde ondergrens voor je nieuwe variabele u gebruikt, namelijk 0 in plaats van 1. Substitutie geeft dit.
[ Bericht 5% gewijzigd door Riparius op 27-06-2012 01:59:48 ]
Ja klopt, was in dat laatste te snel, ondergrens niet vervangen.quote:
[..]
Er komt zo te zien toch iets anders uit.
Je hebt kennelijk na de substitutie u = 1 + 4r2, du = 8rdr de verkeerde ondergrens voor je nieuwe variabele u gebruikt, namelijk 0 in plaats van 1. Substitutie geeft dit.
Je kunt eens beginnen met de site van Dick Klingens. Hier is heel veel te vinden over vlakke meetkunde, met bewijzen, en alles in het Nederlands (hetgeen van belang is omdat je dan ook vertrouwd raakt met de unieke Nederlandse termen voor veel meetkundige begrippen). Maar let op de waarschuwing (met een knipoog naar Plato): Μηδεὶς ἀγεωμέτρητος εἰσίτω μου τὴν στέγην (laat niemand die onkundig is in de meetkunde mijn site binnengaan).quote:
Op 
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |