[Bèta wiskunde] Huiswerk- en vragentopic

quote:

Op donderdag 21 juni 2012 20:30 schreef Amoeba het volgende:
Ik vind het verdomme een schande dat niemand op mijn school nog even door dat werkstuk heen wil kijken dat ik (met dank aan Riparius) had gemaakt. Van die docent wiskunde kreeg ik juist het dringende advies de Mercatorprojectie buiten beschouwing te laten. Terwijl die eerstegraads docent (die tevens examinator is volgende week) het juist wel een goed idee vond. Rampzalige school.

Welkom in de echte wereld, die in handen is van de faalhazen

En waar kan ik naar toe met een klacht. Ik heb zero voorbereiding voor wiskunde B gekregen op het mondeling examen. Er is bij ons geen rector, enkel een kutkop die zichzelf afdelingscoördinator noemt en zij persoonlijke interne begeleiders. Die leggen die klacht naast zich neer. En als ik hem er direct op aanspreek begint hij over ongemotiveerde havistjes te zeuren die een 4,6 gemiddeld staan in de derde klas.

quote:

Op donderdag 21 juni 2012 20:36 schreef Amoeba het volgende:
En waar kan ik naar toe met een klacht. Ik heb zero voorbereiding voor wiskunde B gekregen op het mondeling examen. Er is bij ons geen rector, enkel een kutkop die zichzelf afdelingscoördinator noemt en zij persoonlijke interne begeleiders. Die leggen die klacht naast zich neer. En als ik hem er direct op aanspreek begint hij over ongemotiveerde havistjes te zeuren die een 4,6 gemiddeld staan in de derde klas.

Ik heb snel door de topic gekeken en ik moet zeggen dat je werkstuk wel voorbij vwo wiskunde gaat. Vwo wiskunde stopt namelijk bij de methode van Cavalieri, waarmee je de inhoud van een bol bepaalt. Wel jammer dat het onderwijs in Nederland ook niet goed is gericht op leerlingen die meer kunnen hebben.

quote:

Op donderdag 21 juni 2012 21:07 schreef Mathemaat het volgende:

[..]

Ik heb snel door de topic gekeken en ik moet zeggen dat je werkstuk wel voorbij vwo wiskunde gaat. Vwo wiskunde stopt namelijk bij de methode van Cavalieri, waarmee je de inhoud van een bol bepaalt. Wel jammer dat het onderwijs in Nederland ook niet goed is gericht op leerlingen die meer kunnen hebben.

Meer willen hebben. De kwaliteit van de docenten is sowieso bedroevend. Maar misschien komt dat wel omdat ik geen regulier onderwijs meer volg vanwege een diagnose in het autistisch spectrum.

Ik kom niet uit de volgende opgave:



Het puntje boven de w betekend een tijdsafgeleide zie:
http://en.wikipedia.org/wiki/Newton's_notation

Ik snap niet waarom je zowel met een w als een d moet werken, maar je hebt dus de vector

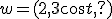
Op de plek van het vraagteken moet de primitieve van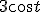 komen, omdat je anders door een lineaire differentiaalvergelijking nooit meer op 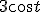kunt uitkomen. Je krijgt dus

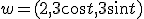
en gevraagd is de matrix S zodanig dat

Dan kom je uit op de matrix van het antwoord.

quote:

Op donderdag 21 juni 2012 21:07 schreef Mathemaat het volgende:

[..]

Ik heb snel door het topic gekeken en ik moet zeggen dat je werkstuk wel voorbij vwo wiskunde gaat.

Dat lijkt me nogal meevallen. Elke goede VWO leerling die die zogeheten 'voortgezette integraalrekening' heeft gevolgd is bekend met zaken als breuksplitsing en de substitutiemethode en zou dus, met wat hulp, in staat moeten worden geacht iets als 1/cos φ te primitiveren.

quote:

Vwo wiskunde stopt namelijk bij de methode van Cavalieri, waarmee je de inhoud van een bol bepaalt. Wel jammer dat het onderwijs in Nederland ook niet goed is gericht op leerlingen die meer kunnen hebben.

Dit is gewoon niet waar, en dat weet je zelf ook wel. Cavalieri leefde in een tijd waarin er van differentiaal- en integraalrekening nog geen sprake was, en op het VWO programma staat in ieder geval de berekening van het volume van een omwentelingslichaam met behulp van integraalrekening.

Overigens maakte Archimedes zo'n 1900 jaar (!) vóór Cavalieri al gebruik van het naar deze laatste genoemde principe. Archimedes realiseerde zich namelijk dat het snijvlak op een hoogte h boven het grondvlak van een halve bol met straal r een oppervlakte π∙(r² - h²) heeft, zodat de oppervlakte van de ring op hoogte h buiten de bol maar binnen de omgeschreven cilinder van de halve bol π∙h² bedraagt, en dus gelijk is aan de oppervlakte van het snijvlak met een (omgekeerde) kegel binnen dezelfde omgeschreven cilinder. Archimedes concludeerde hieruit dat het volume binnen de omgeschreven cilinder maar buiten de halve bol gelijk moest zijn aan het volume van de kegel, zijnde (1/3)∙π∙r²∙r = (1/3)∙π∙r³. En aangezien het totale volume van de omgeschreven cilinder π∙r²∙r = π∙r³ bedraagt, volgt dus dat het volume van de halve bol (2/3)∙π∙r³ moet zijn, waaruit weer volgt dat het volume van een gehele bol met gelijke straal (4/3)∙π∙r³ bedraagt. Archimedes drukte dit uit door te zeggen het het volume van een bol gelijk is aan 2/3 deel van het volume van de omgeschreven cilinder. Hij bewees overigens ook dat de oppervlakte van een bol gelijk is aan de manteloppervlakte van de omgeschreven cilinder, en daarmee weer gelijk aan 2/3 deel van de totale oppervlakte van de omgeschreven cilinder. Zelf beschouwde hij dit als één van zijn fraaiste resultaten.

Strakjes even dit puike stukje historie lezen, altijd leuk.

Verder:

Het primitiveren van de secans met behulp van de voortgezette integraalrekening is inderdaad mogelijk. Echter is het een vele malen ingewikkeldere primitieve om tot te komen dan alle opgaven (zoals: primitiveer f(x) = ln(x)) die in Getal & Ruimte staan beschreven.
Niet om lullig te doen, maar vwo spel je dus enkel met kleine letters.

quote:

Op vrijdag 22 juni 2012 20:18 schreef Amoeba het volgende:
Strakjes even dit puike stukje historie lezen, altijd leuk.

Verder:

Het primitiveren van de secans met behulp van de voortgezette integraalrekening is inderdaad mogelijk. Echter is het een vele malen ingewikkeldere primitieve om tot te komen dan alle opgaven (zoals: primitiveer f(x) = ln(x)) die in Getal & Ruimte staan beschreven.

Ja, hij is lastig, maar toch te doen met de aangereikte methoden. Ik weet eigenlijk niet of dit vroeger aan bod kwam in de hoogste klassen in het Nederlandse of Vlaamse middelbaar onderwijs, moet ik eens proberen te achterhalen.

quote:

Niet om lullig te doen, maar vwo spel je dus enkel met kleine letters.

Vroeger schreef je onderwijs met hoofdletters, nu niet meer. Overigens zie ik bijvoorbeeld op dit correctievoorschrift uit 2009 (nota bene voor het vak Nederlands) toch echt VWO staan.

quote:

Op vrijdag 22 juni 2012 19:33 schreef Riparius het volgende:

[..]

Dat lijkt me nogal meevallen. Elke goede VWO leerling die die zogeheten 'voortgezette integraalrekening' heeft gevolgd is bekend met zaken als breuksplitsing en de substitutiemethode en zou dus, met wat hulp, in staat moeten worden geacht iets als 1/cos φ te primitiveren.

Dat klopt, maar het gaat wel voorbij wiskunde B.

quote:

[..]

Dit is gewoon niet waar, en dat weet je zelf ook wel. Cavalieri leefde in een tijd waarin er van differentiaal- en integraalrekening nog geen sprake was,

Oké, je hebt ook nog de differentiaal- en integraalrekening. Mijn fout.

quote:

Op vrijdag 22 juni 2012 20:49 schreef Riparius het volgende:

[..]

Ja, hij is lastig, maar toch te doen met de aangereikte methoden. Ik weet eigenlijk niet of dit vroeger aan bod kwam in de hoogste klassen in het Nederlandse of Vlaamse middelbaar onderwijs, moet ik eens proberen te achterhalen.

[..]

Vroeger schreef je onderwijs met hoofdletters, nu niet meer. Overigens zie ik bijvoorbeeld op dit correctievoorschrift uit 2009 (nota bene voor het vak Nederlands) toch echt VWO staan.

Mij werd aangeleerd (tijdens het vak Nederlands) dat het vwo is. Misschien zijn die voorbladen al 80 jaar hetzelfde en past niemand het aan.
En wat bedoel je nu, de voortgezette integraalrekening of het primitiveren van de secans?

quote:

Op vrijdag 22 juni 2012 20:53 schreef Mathemaat het volgende:

[..]

Dat klopt, maar het gaat wel voorbij wiskunde B.

[..]

Oké, je hebt ook nog de differentiaal- en integraalrekening. Mijn fout.

Naar mijn mening is het hoofdstuk goniometrie en meetkunde in wiskunde B vele malen moeilijker dan de integraalrekening. De differentiaalrekening is uiteraard appeltje eitje (op vwo niveau dan, om even te nuanceren).

Ik wilde trouwens even zeggen dat m'n tentamen goed was gegaan. Deze herkansing was vele malen makkelijker dan het eerste tentamen. Dus een voldoende moet er zeker in gaan zitten

Alleen jammer dan dat ze niets vroegen over herschrijven van expressies

quote:

Op vrijdag 22 juni 2012 21:03 schreef Amoeba het volgende:

[..]

Mij werd aangeleerd (tijdens het vak Nederlands) dat het vwo is. Misschien zijn die voorbladen al 80 jaar hetzelfde en past niemand het aan.

Het schijnt tegenwoordig (sinds een spellingswijziging van enkele jaren geleden) inderdaad opeens met kleine letters te moeten. De 'regels' (voor zover je daarvan kunt spreken) voor het schrijven van zogeheten letterwoorden zijn sowieso krankzinnig en tegenstrijdig, zodat het onmogelijk is deze regels te volgen. Zo is er een principe dat zegt dat je kleine letters moet gebruiken als het als één woord is uit te spreken, en dan zou je dus wel havo maar geen vwo moeten hebben. En toch heb je dan weer pvc naast DDT. Weer een andere regel zegt dat 'vreemde' letterwoorden eerst met hoofdletters moeten worden geschreven, maar later, als ze zijn ingeburgerd (wie bepaalt dat?), met kleine letters. Zo heb je dus eerst ADSL maar nu adsl, waarmee weer volkomen wordt voorbij gegaan aan het feit dat adsl niet strookt met de foneemdistributie in Nederlandse woorden. Ziekten zijn ook heel leuk: die moeten met hoofdletters, waarbij plotseling de mogelijk vreemdtalige herkomst opeens geen rol meer speelt: MKZ, BSE. Maar als ziekten zijn 'ingeburgerd' (jawel) dan worden het weer kleine letters, zoals aids en tbc. En dan is nog een regel die zegt dat letterwoorden van niet meer dan drie letters met hoofdletters moeten geschreven (ondanks pvc, tbc en vwo). Je begrijpt: niemand kan dit nog volgen en ik weiger mee te doen aan dergelijke idioterie en houd het dus gewoon op VWO.

quote:

En wat bedoel je nu, de voortgezette integraalrekening of het primitiveren van de secans?

Het primitiveren van de secans. Ik bedacht trouwens nog dat je ∫ dφ/√(1 - sin²φ) kunt schrijven (voor |φ| < ½π), en substitutie t = sin φ geeft dan ∫ dt/(1 - t²) en deze laatste integraal is wel zo'n beetje het meest basale voorbeeld dat je kunt bedenken van een integraal die je met breuksplitsing kunt behandelen. Is dus prima te doen.

quote:

[..]

Naar mijn mening is het hoofdstuk goniometrie en meetkunde in wiskunde B vele malen moeilijker dan de integraalrekening. De differentiaalrekening is uiteraard appeltje eitje (op vwo niveau dan, om even te nuanceren).

Vele malen moeilijker? Ik weet dat veel leerlingen tegenwoordig hun goniometrische identiteiten niet meer kennen en ook al niks meer bakken van een eenvoudige bewijsopgave uit de vlakke meetkunde, maar waarom zou vlakke meetkunde of goniometrie moeilijker zijn dan integraalrekening? Soms omdat integreren is verworden tot het gebruik van een formulekaart met een paar standaard primitieven en verder maar gewoon een beetje pielen met de GR als de functie in kwestie toevallig niet op de kaart staat?

quote:

Op vrijdag 22 juni 2012 21:58 schreef Riparius het volgende:

[..]

Het schijnt tegenwoordig (sinds een spellingswijziging van enkele jaren geleden) inderdaad opeens met kleine letters te moeten. De 'regels' (voor zover je daarvan kunt spreken) voor het schrijven van zogeheten letterwoorden zijn sowieso krankzinnig en tegenstrijdig, zodat het onmogelijk is deze regels te volgen. Zo is er een principe dat zegt dat je kleine letters moet gebruiken als het als één woord is uit te spreken, en dan zou je dus wel havo maar geen vwo moeten hebben. En toch heb je dan weer pvc naast DDT. Weer een andere regel zegt dat 'vreemde' letterwoorden eerst met hoofdletters moeten worden geschreven, maar later, als ze zijn ingeburgerd (wie bepaalt dat?), met kleine letters. Zo heb je dus eerst ADSL maar nu adsl, waarmee weer volkomen wordt voorbij gegaan aan het feit dat adsl niet strookt met de foneemdistributie in Nederlandse woorden. Ziekten zijn ook heel leuk: die moeten met hoofdletters, waarbij plotseling de mogelijk vreemdtalige herkomst opeens geen rol meer speelt: MKZ, BSE. Maar als ziekten zijn 'ingeburgerd' (jawel) dan worden het weer kleine letters, zoals aids en tbc. En dan is nog een regel die zegt dat letterwoorden van niet meer dan drie letters met hoofdletters moeten geschreven (ondanks pvc, tbc en vwo). Je begrijpt: niemand kan dit nog volgen en ik weiger mee te doen aan dergelijke idioterie en houd het dus gewoon op VWO

Aangenomen dat dit allemaal klopt geef ik je gelijk.

quote:

Het primitiveren van de secans. Ik bedacht trouwens nog dat je ∫ dφ/√(1 - sin²φ) kunt schrijven (voor |φ| < ½π), en substitutie t = sin φ geeft dan ∫ dt/(1 - t²) en deze laatste integraal is wel zo'n beetje het meest basale voorbeeld dat je kunt bedenken van een integraal die je met breuksplitsing kunt behandelen. Is dus prima te doen.

Dit is wel ongelijk aan het behandelen van de secans. Nu behandel je juist het kwadraat van de secans, wat uiteraard stukken eenvoudiger ligt. Maar dit is inderdaad een vrij eenvoudige breuksplitsing.

quote:

Vele malen moeilijker? Ik weet dat veel leerlingen tegenwoordig hun goniometrische identiteiten niet meer kennen en ook al niks meer bakken van een eenvoudige bewijsopgave uit de vlakke meetkunde, maar waarom zou vlakke meetkunde of goniometrie moeilijker zijn dan integraalrekening? Soms omdat integreren is verworden tot het gebruik van een formulekaart met een paar standaard primitieven en verder maar gewoon een beetje pielen met de GR als de functie in kwestie toevallig niet op de kaart staat?

Ik moet eerlijk bekennen dat ik altijd schuldig was aan het niet kennen van de dubbele hoek formules en dergelijke, (inmiddels wel). Echter moet ik wel altijd nadenken over de gegeven identiteiten voor de tangens, cosinus en sinus. 1/4π Nadenken, niet de GR pakken bedoel ik dan.

Maar goed, over de meetkundige bewijzen. Ik vond het altijd geweldig leuk om Q.E.D. achter mijn redenatie te zetten, maar ik moet eerlijk bekennen dat als ik een examen meetkunde zou krijgen, dat ik er voor zou zakken. En niet omdat ik de gegeven stellingen niet ken die ik dien toe te passen. Goniometrie was wel vrij eenvoudig, maar ik vond het wel moeilijker dan de integraalrekening.

quote:

Op vrijdag 22 juni 2012 21:58 schreef Riparius het volgende:
Vele malen moeilijker? Ik weet dat veel leerlingen tegenwoordig hun goniometrische identiteiten niet meer kennen en ook al niks meer bakken van een eenvoudige bewijsopgave uit de vlakke meetkunde, maar waarom zou vlakke meetkunde of goniometrie moeilijker zijn dan integraalrekening? Soms omdat integreren is verworden tot het gebruik van een formulekaart met een paar standaard primitieven en verder maar gewoon een beetje pielen met de GR als de functie in kwestie toevallig niet op de kaart staat?

Klopt, op de vwo toetsen werden bij differentiëren en integreren bijna alleen maar standaardintegralen en -afgeleiden gevraagd. Bij goniometrie moet je opeens ook echt bewijzen gaan formuleren, wat de meeste mensen tot dan toe nog nooit gedaan hebben (inclusief mezelf, ik had erg veel moeite met dat hoofdstuk). Daarom lijkt goniometrie natuurlijk veel moeilijker, maar dat komt natuurlijk door de methode waarop het behandeld wordt.

Trouwens, ik heb nog een vraag aan jou. Het is duidelijk dat je vrij veel goniometrische identiteiten kent, heb je nog een tip om die te leren? Heb je gewoon een lijst opgezocht en uit je hoofd geleerd, bewijzen bestudeerd, of misschien zelf een bewijs gezocht voor sommige gevallen?
Ik merkte dat die identiteiten inderdaad vaak wel van pas komen, maar ik ken bijna geen goniometrische identiteiten.

quote:

Op vrijdag 22 juni 2012 22:12 schreef Amoeba het volgende:

[..]

Dit is wel ongelijk aan het behandelen van de secans. Nu behandel je juist het kwadraat van de secans, wat uiteraard stukken eenvoudiger ligt.

Nee hoor: ∫ sec φ∙dφ = ∫ dφ/√(1 - sin²φ)

quote:

Maar dit is inderdaad een vrij eenvoudige breuksplitsing.

Precies.

quote:

[..]

Ik moet eerlijk bekennen dat ik altijd schuldig was aan het niet kennen van de dubbele hoek formules en dergelijke, (inmiddels wel). Echter moet ik wel altijd nadenken over de gegeven identiteiten voor de tangens, cosinus en sinus. 1/4π

Je bedoelt cos(π/4) = sin(π/4) = ½√2 en zo? Of sin(¼π - φ) = cos(¼π + φ) of tan(¼π - φ)∙tan(¼π + φ) = 1 (nee, die staan vast niet op je formulekaart).

quote:

Nadenken, niet de GR pakken bedoel ik dan.

Maar goed, over de meetkundige bewijzen. Ik vond het altijd geweldig leuk om Q.E.D. achter mijn redenatie te zetten, maar ik moet eerlijk bekennen dat als ik een examen meetkunde zou krijgen, dat ik er voor zou zakken. En niet omdat ik de gegeven stellingen niet ken die ik dien toe te passen. Goniometrie was wel vrij eenvoudig, maar ik vond het wel moeilijker dan de integraalrekening.

Als je wiskunde wil gaan studeren lijkt me een goed meetkundig inzicht toch ook wel belangrijk. Meetkunde heeft in vroeger tijden ook heel lang de hoofdmoot gevormd van het wiskunde onderwijs vanwege de streng axiomatische opbouw en de oefening die dat gaf in het opstellen van strict deductieve redeneringen (bewijzen dus). Oudere generaties herinneren het zich nog: Gegeven: ..., Te bewijzen: ..., Bewijs: ... Sterker nog, wiskunde wás meetkunde in vroeger tijden, en een wiskundige werd toen ook een geometer genoemd (het woord geometrie betekent eigenlijk landmeetkunde en verwijst dus naar de praktische oorsprong).

Och verrek, met jouw unicode had ik dat wortelteken helemaal niet gezien. Pas in vierde instantie.
Ik heb er wel veel op zitten oefenen. Het lukte me ook beter en beter, maar aangezien het examen zo verrekte lang was heb ik die maar uitgesteld tot het laatste waardoor ik er 2 niet af had. Beetje jammer.

En ja, ik bedoelde die goniometrische identiteiten. Maar ik ga ze leren.

quote:

Op vrijdag 22 juni 2012 21:19 schreef Juicyhil het volgende:
Ik wilde trouwens even zeggen dat m'n tentamen goed was gegaan. Deze herkansing was vele malen makkelijker dan het eerste tentamen. Dus een voldoende moet er zeker in gaan zitten

Alleen jammer dan dat ze niets vroegen over herschrijven van expressies

Mooi. Sowieso wel handig om dat soort dingen te snappen, het is gewoon basislogica die je gewoon in het dagelijks leven kan toepassen. Als je die regels snapt merk je ook sneller redeneerfouten op van anderen. Wat studeer je eigenlijk?

Ik bedacht trouwens nog dat je ∫ dφ/√(1 - sin²φ) kunt schrijven (voor |φ| < ½π), en substitutie t = sin φ geeft dan ∫ dt/(1 - t²)

- Riparius

Kun je even uitleggen waarom je nu ineens wel dat wortelteken weglaat ná je substitutie?

quote:

Op vrijdag 22 juni 2012 23:02 schreef Amoeba het volgende:
Och verrek, met jouw unicode had ik dat wortelteken helemaal niet gezien. Pas in vierde instantie.
Ik heb er wel veel op zitten oefenen. Het lukte me ook beter en beter, maar aangezien het examen zo verrekte lang was heb ik die maar uitgesteld tot het laatste waardoor ik er 2 niet af had. Beetje jammer.

Geldt ook voor mij. Eigenlijk alles van wiskunde B ging me makkelijk af, behalve goniometrie. Ik heb uiteindelijk geloof ik nog steeds geen voldoende voor die toets gehaald . Maar het inzicht komt inderdaad ook wel met oefenen, gelukkig. Ik moet zeggen, ik heb nog niet veel moeilijke goniometrie gehad bij mijn studie wiskunde (bij lineaire algebra en infinitesimaalrekening/calculus een beetje). Maar ik volg dan ook geen concrete meetkunde, wat volgens mij nog wel vrij veel op goniometrie lijkt.

quote:

Op vrijdag 22 juni 2012 23:06 schreef Amoeba het volgende:
Ik bedacht trouwens nog dat je ∫ dφ/√(1 - sin²φ) kunt schrijven (voor |φ| < ½π), en substitutie t = sin φ geeft dan ∫ dt/(1 - t²)

- Riparius

Kun je even uitleggen waarom je nu ineens wel dat wortelteken weglaat ná je substitutie?

Je verwisselt ook nog de dphi met dt.

Omdat

geldt

quote:

Op vrijdag 22 juni 2012 23:53 schreef kutkloon7 het volgende:

[..]

Geldt ook voor mij. Eigenlijk alles van wiskunde B ging me makkelijk af, behalve goniometrie. Ik heb uiteindelijk geloof ik nog steeds geen voldoende voor die toets gehaald . Maar het inzicht komt inderdaad ook wel met oefenen, gelukkig. Ik moet zeggen, ik heb nog niet veel moeilijke goniometrie gehad bij mijn studie wiskunde (bij lineaire algebra en infinitesimaalrekening/calculus een beetje). Maar ik volg dan ook geen concrete meetkunde, wat volgens mij nog wel vrij veel op goniometrie lijkt.

Ik weet nog dat ik goniometrie ook lastig vond, met name het bewijzen van goniometrische identiteiten. Sinds de middelbare school heb ik er niks aan gedaan, maar nu vind ik die sommetjes juist heel erg eenvoudig. Volgens mij was het probleem vooral dat ik niet in één keer kon zien dat een bepaalde identiteit gold, waardoor je direct dacht van "ik snap het niet". Terwijl, als je gewoon domweg wat identiteiten toepast kom je er bij die sommen zo'n beetje automatisch.

Maar goed, gonio en meetkunde is allemaal leuk en aardig om mee te oefenen, maar wel een beetje overrated op de middelbare school naar mijn mening.

quote:

Op vrijdag 22 juni 2012 22:47 schreef kutkloon7 het volgende:

[..]

Klopt, op de vwo toetsen werden bij differentiëren en integreren bijna alleen maar standaardintegralen en -afgeleiden gevraagd. Bij goniometrie moet je opeens ook echt bewijzen gaan formuleren, wat de meeste mensen tot dan toe nog nooit gedaan hebben (inclusief mezelf, ik had erg veel moeite met dat hoofdstuk). Daarom lijkt goniometrie natuurlijk veel moeilijker, maar dat komt natuurlijk door de methode waarop het behandeld wordt.

Inderdaad, ik word niet vrolijk van wat ik van de huidige lesmethoden heb gezien, en het is geen wonder dat het met het inzicht vaak niet best is gesteld. In Vlaanderen gaat dat beter, daar wordt nog (enigszins) ouderwets onderwijs gegeven. Een tijd geleden stond er op de site beteronderwijsnederland.nl een aardig overzicht van een zomercursus van de KU Leuven die je als opfrisser zou kunnen doornemen. De link is helaas verdwenen, maar gelukkig wel gearchiveerd door archive.org en hier nog te zien.

quote:

Trouwens, ik heb nog een vraag aan jou. Het is duidelijk dat je vrij veel goniometrische identiteiten kent, heb je nog een tip om die te leren? Heb je gewoon een lijst opgezocht en uit je hoofd geleerd, bewijzen bestudeerd, of misschien zelf een bewijs gezocht voor sommige gevallen?
Ik merkte dat die identiteiten inderdaad vaak wel van pas komen, maar ik ken bijna geen goniometrische identiteiten.

Ik heb ze nooit echt uit het hoofd geleerd, en dat zou ik je ook niet aanraden. Maar ik ben wel gezegend met een goed geheugen, en ik ken ze gewoon al van jongs af aan (en dat is echt heel lang geleden). Belangrijk is vooral dat je inzicht hebt (of krijgt) in de reden waarom die identiteiten zijn zoals ze zijn. Bijvoorbeeld, bij

cos²φ + sin²φ = 1

denk je aan de eenheidscirkel. Aangezien cos φ en sin φ zijn gedefinieerd als resp. de x-coördinaat en de y-coördinaat van het beeldpunt van (1;0) bij rotatie om de oorsprong over een hoek φ en de eenheidscirkel de vergelijking x² + y² = 1 heeft, is het evident dat deze identiteit geldt. Je kunt deze identiteit ook als een goniometrische variant van de stelling van Pythagoras zien.

Fundamenteel is ook dat de cosinusfunctie een even functie is en de sinusfunctie een oneven functie. Dat wil zeggen dat:

cos(-φ) = cos φ
sin(-φ) = -sin φ

Om dit in te zien denk je aan het startpunt (1;0) op de eenheidscirkel. Als we dit startpunt roteren over een hoek -φ en over een hoek φ, dan liggen de twee beeldpunten van (1;0) symmetrisch t.o.v. de x-as, omdat het startpunt zelf op de x-as ligt. En dat betekent dat deze twee beeldpunten dezelfde x-coördinaat hebben, maar een tegengestelde y-coördinaat. En aangezien de x-coördinaat van het beeldpunt per definitie de cosinus is van de rotatiehoek en de y-coördinaat de sinus, geldt dus inderdaad cos(-φ) = cos φ en sin(-φ) = -sin φ.

Tegengestelde hoeken (rotaties) corresponderen dus met een spiegeling in de x-as, maar supplementaire hoeken corresponderen met een spiegeling in de y-as, waarbij de x-coördinaat tegengesteld wordt en de y-coördinaat hetzelfde blijft, zodat cos(π-φ) = -cos φ en sin(π-φ) = sin φ. En bij complementaire hoeken hebben we een spiegeling in de lijn y = x zodat de x- en de y-coördinaten omwisselen en dus cos(½π-φ) = sin φ en sin(½π-φ) = cos φ.

Bij de formule van De Moivre

(cos φ + i∙sin φ)ⁿ = cos nφ + i∙sin nφ

kun je denken aan de fundamentele eigenschap van complexe getallen dat vermenigvuldiging met een complex getal meetkundig overeenkomt met een draaistrekking. Is de modulus van het getal waarmee je vermenigvuldigt gelijk aan één, dan heb je geen strekking en (dus) alleen een rotatie. Vermenigvuldiging met cos φ + i∙sin φ betekent een rotatie tegen de klok in over een hoek φ. Als we dus beginnen met het getal 1 en dat n maal achtereen vermenigvuldigen met cos φ + i∙sin φ dan hebben we uiteindelijk vermenigvuldigd met (cos φ + i∙sin φ)ⁿ. Elke vermenigvuldiging gaf een rotatie over een hoek φ en dus hebben we in totaal een rotatie over een hoek nφ wat betekent dat dit precies hetzelfde is als direct vermenigvuldigen met cos nφ + i∙sin nφ, waarmee de formule inzichtelijk is geworden.

Vermenigvuldig je een complex getal eerst met cos α + i∙sin α en dan het resultaat weer met cos β + i∙sin β, dan roteren we eerst over een hoek α en dan nog eens over een hoek β, wat dus betekent dat we in totaal over een hoek α + β hebben geroteerd en we dus net zo goed meteen met cos(α+β) + i∙sin(α+β) hadden kunnen vermenigvuldigen om hetzelfde resultaat te krijgen. Dus hebben we:

cos(α+β) + i∙sin(α+β) = (cos α + i∙sin α)(cos β + i∙sin β)

Uitwerken van de haakjes in het rechterlid en gebruik maken van i² = -1 geeft:

cos(α+β) + i∙sin(α+β) = (cos α∙cos β - sin α∙sin β) + i∙(sin α∙cos β + cos α∙sin β)

En omdat twee complexe getallen alleen aan elkaar gelijk zijn als zowel de reële als de imaginaire delen aan elkaar gelijk zijn hebben we dus:

cos(α+β) = cos α∙cos β - sin α∙sin β
sin(α+β) = sin α∙cos β + cos α∙sin β

Dit zijn de bekende additietheorema's voor de cosinus en de sinus die vaak lastig worden gevonden. Maar je ziet dat ze heel gemakkelijk zijn af te leiden. Het patroon dat er in zit is ook heel gemakkelijk te herkennen (en dus te onthouden!) als je weet dat (x₁ + iy₁)(x₂ + iy₂) = (x₁x₂ - y₁y₂) + i(y₁x₂ + x₁y₂).

Nog eenvoudiger wordt het als je denkt aan de formule van Euler, die een verband geeft tussen een e-macht met een (zuiver imaginaire) exponent iφ en een rotatiehoek φ:

e^iφ = cos φ + i∙sin φ

Ook hier geldt weer dat je dit gemakkelijk onthoudt als je begrijpt wat dit meetkundig betekent zoals ik wel eens heb uitgelegd.

De functie z(t) = e^it voldoet aan z'(t) = i∙z(t) en z(0) = 1, wat betekent dat dit een parametervoorstelling is van de eenheidscirkel in het complexe vlak. Immers, vermenigvuldiging met i betekent een rotatie over een rechte hoek tegen de klok in, en dus betekent z'(t) = i∙z(t) een curve (baan) waarbij de raaklijn aan de curve (in de richting van z'(t)) steeds loodrecht staat op het lijnstuk vanuit de oorsprong naar het raakpunt z(t). En dat kan alleen maar een cirkel rond de oorsprong zijn, want alleen bij een cirkel staat een raaklijn steeds loodrecht op de straal. En omdat we starten in het punt z(0) = 1 is het de eenheidscirkel, zodat |z(t)| constant is, en wel |z(t)| = 1.

En dat niet alleen, omdat |z(t)| = 1 en dus ook |z'(t)| = |i∙z(t)| = |i|∙|z(t)| = 1∙1 = 1 is het ook nog eens een speciale parametrisatie van de eenheidscirkel, namelijk een booglengteparametrisatie. Dat betekent dat de parameter t de booglengte geeft vanaf het startpunt z(0) = 1, of, als je het 'fysisch' wil bekijken, de afgelegde weg op tijdstip t van een puntdeeltje dat eenparig met een snelheid één (eenheid per eenheid van tijd) tegen de klok in langs de eenheidcirkel beweegt, te beginnen in het punt (1;0) op tijdstip t = 0.

Omdat de gebruikelijke meetkundige definitie van de cosinus en sinus aan de hand van de eenheidscirkel impliceert dat x(t) = cos t, y(t) = sin t een booglengteparametrisatie van de eenheidcirkel geeft met startpunt (1;0), kunnen we de curve z(t) = x(t) + i∙y(t) in het complexe vlak die wordt gekarakteriseerd door z'(t) = i∙z(t), z(0) = 1 evengoed beschrijven als z(t) = cos t + i∙sin t, zodat e^it dus niets anders is dan cos t + i∙sin t.

Omgekeerd betekent dit dat we cos(α+β) + i∙sin(α+β) = (cos α + i∙sin α)(cos β + i∙sin β) ook kunnen schrijven als:

e^i(α+β) = e^iα∙e^iβ

De formule van Euler impliceert dus eigenlijk dat het optellen van rotatiehoeken bij vermenigvuldiging van complexe getallen niets anders is dan het optellen van (zuiver imaginaire) exponenten bij vermenigvuldiging van twee e-machten. De bekende additieformules voor cos(α+β) en sin(α+β) kun je dus zien als een andere gedaante van e^i(α+β) = e^iα∙e^iβ en daarmee als een manifestatie van iets veel fundamentelers, namelijk een verband tussen rotatie en vermenigvuldiging van complexe getallen. Ook de formule van De Moivre kun je zo in een bijzonder eenvoudige vorm brengen, namelijk:

(e^iφ)ⁿ = e^inφ

Het is misschien instructief om nog even te laten zien dat je alle eigenschappen van de cosinus en de sinus functie ook zonder meetkundige beschouwingen af kunt leiden uit een complexe functie z(t) = x(t) + i∙y(t) van een reële variabele t die voldoet aan z'(t) = i∙z(t), z(0) = 1.

Duiden we de geconjugeerde van z(t) aan met z*(t) = x(t) - i∙y(t) dan is |z(t)|² = z(t)∙z*(t) en is de afgeleide van |z(t)|² dus d(|z(t)|²)/dt = z'(t)∙z*(t) + z(t)∙z*'(t) = i∙z(t)∙z*(t) + z(t)∙(z'(t))* = i∙z(t)∙z*(t) + z(t)∙(i∙z(t))* = i∙z(t)∙z*(t) + z(t)∙(-i)∙z*(t) = 0, zodat z(t)∙z*(t) = |z(t)|² en dus ook |z(t)| constant moet zijn. En aangezien z(0) = 1 geldt dus |z(t)| = 1 voor elke reële waarde van t. Zo hebben we dus

z(t)∙z*(t) = 1

oftewel:

(x(t))² + (y(t))² = 1.

Uit |z(t)| = 1 volgt zoals we al gezien hebben |z'(t)| = 1 en dus s(t) = ∫₀^t |z'(τ)|∙dτ = t, zodat we een booglengteparametrisatie van de eenheidscirkel hebben.

Kijken we nu naar de afgeleide van z(t)∙z(-t), dan vinden we d(z(t)∙z(-t))/dt = z'(t)∙z(-t) + z(t)∙z'(-t)∙(-1) = i∙z(t)∙z(-t) + z(t)∙i∙z(-t)∙(-1) = 0, zodat z(t)∙z(-t) constant is en wel gelijk aan z(0)∙z(0) = 1. Uit z(t)∙z(-t) = 1 en z(t)∙z*(t) = 1 volgt

z(-t) = z*(t)

oftewel

x(-t) = x(t) en y(-t) = -y(t),

zodat we kunnen concluderen dat x(t) een even functie en y(t) een oneven functie is. Is nu c een willekeurige reële constante, dan kunnen we door de afgeleide te bepalen van z(t)∙z(c - t) op dezelfde wijze constateren dat dit ook een constante moet zijn, en aangezien we voor t = 0 hebben z(0)∙z(c - 0) = 1∙z(c) = z(c) hebben we dus z(t)∙z(c - t) = z(c) voor elke reële c en t. Substitutie van t = α en c = α + β (en dus c - t = β) geeft dan

z(α)∙z(β) = z(α+β)

Bedenken we nu dat z(t) = x(t) + i∙y(t) met z'(t) = i∙z(t), z(0) = 1 een booglengteparametrisatie van de eenheidscirkel voorstelt en dat dus op grond van de conventionele definitie van de cosinus en de sinus aan de hand van de eenheidscirkel moet gelden x(t) = cos t en y(t) = sin t, dan zie je dat we alle belangrijke eigenschappen van de sinus en cosinus terug hebben gevonden: uit z(t)∙z*(t) = 1 volgt (cos t + i∙sin t)(cos t - i∙sin t) = 1 oftewel cos²t + sin²t = 1, uit z(-t) = z*(t) volgt cos(-t) = cos t en sin(-t) = -sint, en z(α+β) = z(α)∙z(β) levert de additietheorema's voor cos(α+β) en sin(α+β). Merk nog op dat z'(t) = i∙z(t) impliceert dat z'(t) = z(t + ½π) aangezien i = z(½π) zodat ook x'(t) = x(t + ½π) en y'(t) = y(t + ½π) en dus d(cos t)/dt = cos(t + ½π) = -sin t en d(sin t)/dt = sin(t + ½π) = cos t. Zo zie je waarom je na viermaal differentiëren van cos t of sin t weer terug bent bij de oorspronkelijke functie, omdat cos t en sin t een periode 2π = 4∙½π hebben.

Nu zul je misschien zeggen, goed dat is allemaal interessant en mooi om de formules voor cos(α+β) en sin(α+β) te onthouden, maar zo heb ik het op school niet geleerd. Kan het ook zonder complexe getallen? Ja, dat kan zeker, en dat zou in de schoolstof aan bod moeten komen, maar ik heb de indruk dat dat niet goed meer of wellicht helemaal niet meer wordt uitgelegd. Er is een bijzonder elegant en eenvoudig bewijs mogelijk voor de additietheorema's met behulp van vectoren en uitgaande van de definitie van de cosinus en de sinus aan de hand van de eenheidscirkel waarvoor geen kennis buiten de normale schoolstof is vereist. Dit bewijs heeft bovendien het belangrijke voordeel, in tegenstelling tot andere meetkundige bewijzen die ik heb gezien, dat het geldig is voor willekeurige hoeken (rotaties) zowel in positieve als in negatieve zin. Als je dit bewijs wil bestuderen (aanbevolen) dan kun je het hier vinden.

Goed, we hebben nu het analogon cos²φ + sin²φ = 1 van de stelling van Pythagoras gezien, we begrijpen dat de cosinus een even functie is en de sinus een oneven functie, en we hebben de additietheorema's voor cos(α+β) en sin(α+β) gezien. En eigenlijk is dit alles wat je echt nodig hebt, alle andere goniometrische identiteiten laten zich hieruit afleiden. Aangezien α - β = α + (-β) en cos(-β) = cos β en sin(-β) = -sin β vind je met de formules voor cos(α+β) en sin(α+β) gemakkelijk dat ook geldt:

cos(α-β) = cos α∙cos β + sin α∙sin β
sin(α-β) = sin α∙cos β - cos α∙sin β

Stel je β = α in de formules voor cos(α+β) en sin(α+β), dan vind je de formules voor de dubbele hoek:

cos 2α = cos²α - sin²α
sin 2α = 2∙sinα∙cosα

In de formule voor cos 2α zie je kwadraten cos²α en sin²α verschijnen, die we ook hebben in cos²α + sin²α = 1. Dat betekent dat we hier cos²α = 1 - sin²α óf sin²α = 1 - cos²α kunnen substitueren, zodat we nog twee formules voor cos 2α krijgen, namelijk:

cos 2α = 2∙cos²α - 1
cos 2α = 1 - 2∙sin²α

Het nut van deze twee extra formules is vooral dat je hiermee een kwadraat van een cosinus of sinus kunt uitdrukken in de cosinus van de dubbele hoek, als volgt:

cos²α = ½(1 + cos 2α)
sin²α = ½(1 - cos 2α)

Deze formules komen van pas bij de integraalrekening.

Uit de formules de sinus en cosinus van de som en het verschil van twee hoeken kun je ook weer formules afleiden om een som of verschil van twee sinussen of cosinussen om te zetten in een product, of omgekeerd. Tellen we bijvoorbeeld de formules voor cos(α+β) en cos(α-β) bij elkaar op, dan krijgen we:

cos(α+β) + cos(α-β) = 2∙cosα∙cosβ

Stellen we nu α + β = θ en α - β = φ, dan is α = ½(θ + φ) en β = ½(θ - φ) en hebben we dus:

cos θ + cos φ = 2∙cos½(θ + φ)∙cos½(θ - φ)

Op analoge wijze kun je ook formules voor cos θ - cos φ, sin θ + sin φ en sin θ - sin φ afleiden. Dit zijn de regels van Simpson (soms ook de formules van Mollweide genoemd).

Formules voor de sinus of cosinus van de drievoudige hoek komen ook wel eens van pas (casus irreducibilis bij kubische vergelijkingen!). Deze kun je afleiden uit de additietheorema's door uit te gaan van cos 3α = cos(2α + α) en sin 3α = sin(2α + α) en dan uit te werken en de reeds gekende formules voor cos 2α en sin 2α te substitueren. Maar het kan ook eleganter en eenvoudiger met De Moivre. Nemen we n = 3 in de formule van De Moivre, dan krijgen we:

cos 3φ + i∙sin 3φ = (cos + i∙sin φ)³

Uitwerken met behulp van het merkwaardig product (a+b)³ = a³ + 3a²b + 3ab² + b³ geeft:

cos 3φ + i∙sin 3φ = cos³φ + 3∙i∙cos²φ∙sinφ + 3∙i²cosφ∙sin²φ + i³∙sin³φ

cos 3φ + i∙sin 3φ = (cos³φ - 3∙cosφ∙sin²φ) + i∙(3∙cos²φ∙sinφ - sin³φ)

cos 3φ + i∙sin 3φ = (cos³φ - 3∙cosφ + 3∙cos³φ) + i∙(3∙sinφ - 3∙sin³φ - sin³φ)

En dus vinden we door gelijkstelling van de reële en imaginaire delen:

cos 3φ = 4∙cos³φ - 3∙cosφ
sin 3φ = 3∙sinφ - 4∙sin³φ

Tot nu toe hebben we alleen gekeken naar de sinus en cosinus, maar je hebt natuurlijk ook nog de tangens, cotangens, secans en cosecans die als volgt zijn gerelateerd aan de sinus en cosinus:

tan α = sin α/cos α, cot α = cos α/sin α, sec α = 1/cos α, csc α = 1/sin α

Er bestaan nog veel meer goniometrische functies zoals de sinus versus (versin), cosinus versus (coversin), halve sinus versus (haversin), halve cosinus versus (hacoversin), exsecans (exsec), excosecans (excsc) en niet te vergeten de koorde (crd α = 2∙sin ½α), maar die zul je wel zelden of nooit meer tegenkomen, tenzij je je gaat specialiseren in historische wiskunde.

Uiteraard laten alle goniometrische identiteiten waarin een tangens, cotangens, secans of cosecans voorkomt zich herleiden uit de basisidentiteiten voor de sinus en cosinus. Delen we bijvoorbeeld de leden van de identiteit cos²α + sin²α = 1 door cos²α en door sin²α dan krijgen we respectievelijk:

1 + tan²α = sec²α
cot²α + 1 = csc²α

En willen we bijvoorbeeld formules afleiden voor tan(α+β) en tan(α-β) dan gaan we uit van tan(α+β) = sin(α+β)/cos(α+β) en tan(α-β) = sin(α-β)/cos(α-β) en vinden we na substitutie van de uitdrukkingen voor sin(α+β), cos(α+β), sin(α-β) en cos(α-β) en deling van teller en noemer van de breuken door cosα∙cosβ dat

tan(α+β) = (tan α + tan β)/(1 - tan α∙tan β)
tan(α-β) = (tan α - tan β)/(1 + tan α∙tan β)

En door β = α te stellen in de formule voor tan(α+β) krijgen we nog:

tan 2α = 2∙tan α/(1 - tan²α)

Uiteraard hadden we de formule voor de tangens van de dubbele hoek ook kunnen verkrijgen uit tan 2α = sin 2α/cos 2α. Nuttig is nog dat we sin 2α en cos 2α ook uitsluitend in tan α uit kunnen drukken. Delen we de reeds gevonden uitdrukkingen door cos²α + sin²α (waardoor er dus niets verandert, aangezien dit gelijk is aan 1), dan hebben we cos 2α = (cos²α - sin²α)/(cos²α + sin²α) en sin 2α = 2∙sin α∙cos α/(cos²α + sin²α). Delen van teller en noemer van de breuken door cos²α geeft dan:

cos 2α = (1 - tan²α)/(1 + tan²α)
sin 2α = 2∙tan α/(1 + tan²α)

Stellen we nu α = ½φ en dus 2α = φ, en

t = tan ½φ

dan hebben we

cos φ = (1 - t²)/(1 + t²), sin φ = 2t/(1 + t²), tan φ = 2t/(1 - t²),

terwijl uit t = tan ½φ ook volgt dt/dφ = ½(1 + tan²½φ) = ½(1 + t²) en dus

dφ = 2dt/(1 + t²)

Dit zijn de bekende substitutieformules voor de tangens van de halve hoek, ook bekend als de Weierstraß substitutie, die je kunt gebruiken voor het herleiden van integralen waarbij de integrand een rationale functie van sinus en cosinus is.

Dit is natuurlijk maar een kleine greep uit de enorme hoeveelheid goniometrische identiteiten. Voor een overzicht kun je hier of (uitgebreider) hier kijken.

@Riparius

quote:

Dat lijkt me nogal meevallen. Elke goede VWO leerling die die zogeheten 'voortgezette integraalrekening' heeft gevolgd is bekend met zaken als breuksplitsing en de substitutiemethode en zou dus, met wat hulp, in staat moeten worden geacht iets als 1/cos φ te primitiveren.

Het probleem zal eerder de zwakke beheersing van de 'algebraïsche' fundamenten zijn. Dat heb ik gemerkt bij een ingangstest/instaptoets of hoe je het ook wil noemen. De meeste vragen testten slechts 1 fundament, je wil niet weten hoeveel personen een onvoldoende behaalden. Bij calculus bleek eveneens dat studenten vastliepen doordat ze de fundamenten niet beheersten. Nu waren niet al deze studenten goede VWO-leerlingen maar ook een aanzienlijk deel van de studenten die dat wel waren hadden hier problemen mee.

@Xero

quote:

Ik weet nog dat ik goniometrie ook lastig vond, met name het bewijzen van goniometrische identiteiten. Sinds de middelbare school heb ik er niks aan gedaan, maar nu vind ik die sommetjes juist heel erg eenvoudig. Volgens mij was het probleem vooral dat ik niet in één keer kon zien dat een bepaalde identiteit gold, waardoor je direct dacht van "ik snap het niet". Terwijl, als je gewoon domweg wat identiteiten toepast kom je er bij die sommen zo'n beetje automatisch.

Dat is herkenbaar.
Na een tijdje merk je dat er steeds weer dezelfde truucjes worden gebruikt in een ietwat gewijzigde vorm.

quote:

Maar goed, gonio en meetkunde is allemaal leuk en aardig om mee te oefenen, maar wel een beetje overrated op de middelbare school naar mijn mening.

Ja en nee. Die koordenvierhoeken en congruentie zijn stof voor de eerste paar jaar van het VWO (congruentie was vroeger trouwens ook MAVO-stof). De meetkunde die bij wiskunde D wordt gegeven zou daarentegen juist wel bij wiskunde B moeten worden gegeven.

[ Bericht 40% gewijzigd door Bram_van_Loon op 23-06-2012 12:09:51 ]

Voor wie het interesseert, hier kan je de complete zomercursus van de KULeuven krijgen: http://set.kuleuven.be/ap(...)modules_wiskunde.php
Je moet wel eventjes je e-mailadres opgeven zodat het wordt opgestuurd, je kan het niet direct downloaden.

Je kan ook twee testjes afleggen waarmee wordt ingeschat of dat je basis goed genoeg is om te starten met een opleiding waarbinnen wiskunde een wat prominentere rol speelt. http://www.kuleuven-kulak(...)zomercursus-wiskunde