SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Oh ik had zomaar 2*-5 gedaan :S. Maar harstikke bedankt ik ga nu beter mijn ogen open houden xD.quote:Op zaterdag 16 juni 2012 11:30 schreef PizzaGeit het volgende:
[..]
Ik heb geen idee hoe je aan die 100a komt, maar als je zowel de x als de y invult krijg je dit:


Hoi, ik wil niet irritant zijn maar toch wil ik graag nog één vraag stellen, omdat mijn volgende berekening nog niet lukt.
Bepaal de functie van de parabool als de parabool de x-as snijdt voor x=-1 en x=1
en als verder nog gegeven is dat de top op de lijn y=5 ligt.
f(x)=...
Zo heb ik het aangepakt:
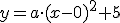
Door het punt (-1,0)
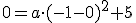
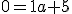
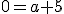
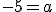
Als antwoord heb ik dan:
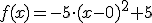
Maar het juiste antwoord is:
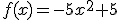
Mijn vraag is: hoe krijg ik het juiste antwoord? Alvast bedankt voor uw antwoord.
Bepaal de functie van de parabool als de parabool de x-as snijdt voor x=-1 en x=1
en als verder nog gegeven is dat de top op de lijn y=5 ligt.
f(x)=...
Zo heb ik het aangepakt:
Door het punt (-1,0)
Als antwoord heb ik dan:
Maar het juiste antwoord is:
Mijn vraag is: hoe krijg ik het juiste antwoord? Alvast bedankt voor uw antwoord.


Oke dus beide antwoorden zijn dus goed? Die computer zei dat mijn antwoord fout was :S.quote:Op zaterdag 16 juni 2012 13:15 schreef PizzaGeit het volgende:
x-0 is hetzelfde als x
Dus je hebt het gewoon goed gedaan
En 1a is toch hetzelfde als a of niet? Nog dankjewel voor je antwoord


De computer wil waarschijnlijk dat je het vereenvoudigt. In principe is -5*1 ( x+0-0*0+0+0)^2 +10 - 6 + 1 ook goed, maar dat zal ook fout gerekend worden.
En ja... 1*a = 1a = a
En ja... 1*a = 1a = a


Dat is dus ook de reden waarom ze meestal computers niet laten nakijkenquote:Op zaterdag 16 juni 2012 13:24 schreef superky het volgende:
[..]
Oke dus beide antwoorden zijn dus goed? Die computer zei dat mijn antwoord fout was :S.
En 1a is toch hetzelfde als a of niet? Nog dankjewel voor je antwoord
Het kan trouwens wel, computers antwoorden laten vereenvoudigen, maar meestal willen leraren dat je zelf ook dingen kan vereenvoudigen (breuken bijvoorbeeld worden soms foutgerekend als ze niet vereenvoudigd zijn).
Maar bij sommige dingen is dan weer onduidelijk wat het meest vereenvoudigd is, bijvoorbeeld: 5x/3 of 5/3 x. Daarom is het meestal makkelijker met de hand na te kijken
Trouwens, als je een beetje strenge leraar hebt zou die dingen als x-0 niet vereenvoudigen ook nog wel fout kunnen rekenen.


Zeker als er "vereenvoudig je antwoord zoveel mogelijk" o.i.d. staat.quote:Op zaterdag 16 juni 2012 14:04 schreef kutkloon7 het volgende:
[..]
Trouwens, als je een beetje strenge leraar hebt zou die dingen als x-0 niet vereenvoudigen ook nog wel fout kunnen rekenen.


Een computer zegt helemaal niets, hooguit een computerprogramma. Wat zegt datzelfde programma als je f(x) = 5 - 5x2 of f(x) = 5(1 - x2) als antwoord zou geven?quote:Op zaterdag 16 juni 2012 13:24 schreef superky het volgende:
[..]
Oke dus beide antwoorden zijn dus goed? Die computer zei dat mijn antwoord fout was :S.
En 1a is toch hetzelfde als a of niet? Nog dankjewel voor je antwoord
Overigens zou het helpen als je eens vertelt wat je precies moet bestuderen voor dat toelatingsexamen dat je kennelijk wil gaan afleggen, en welk boek of welke cursus je daarvoor gebruikt. Ik heb het idee dat je steeds stukloopt op zaken die nog stukken elementairder zijn dan de stof die je geacht wordt te bestuderen, wat dus betekent dat je het examen zo in ieder geval niet gaat halen.


Ik had wel opgeschreven wat de computer als antwoord gaf, het waren er twee:quote:Op zaterdag 16 juni 2012 18:04 schreef Riparius het volgende:
[..]
Een computer zegt helemaal niets, hooguit een computerprogramma. Wat zegt datzelfde programma als je f(x) = 5 - 5x2 of f(x) = 5(1 - x2) als antwoord zou geven?
Overigens zou het helpen als je eens vertelt wat je precies moet bestuderen voor dat toelatingsexamen dat je kennelijk wil gaan afleggen, en welk boek of welke cursus je daarvoor gebruikt. Ik heb het idee dat je steeds stukloopt op zaken die nog stukken elementairder zijn dan de stof die je geacht wordt te bestuderen, wat dus betekent dat je het examen zo in ieder geval niet gaat halen.
Of
De computer genereert telkens een andere vraag en die vraag heb ik niet meer voor mijn neus. Maar ik zal wel de manier waarop je je antwoorden hebt geschreven eens gaan gebruiken als ik weer zo'n vraag krijg.
Het is een zomercursus van de HvA en ik heb ook een boek HTO basisvaardigheden wiskunde (2e herziene druk ISBN: 978-90-01-76438-8) van Noordhoff Uitgevers. Maar ik leer niet uit het boek, ik oefen, nadat de docent uitleg heeft gegeven, op de computer omdat die vragen ook worden gesteld tijdens de toets.


Je begrijpt dat je de wiskunde achter een vraagstuk moet snappen alvorens je een vraagstuk volledig kan begrijpen? Mensen die wiskunde proberen op te lossen aan de hand van vaste regeltjes komen over het algemeen niet ver, wiskunde is begrijpen. Klinkt een beetje hard, maar als je vast blijft lopen op deze opgaven heb je duidelijk niet begrepen hoe een functievoorschrift van een parabool in elkaar zit.quote:Op zaterdag 16 juni 2012 18:30 schreef superky het volgende:
[..]
Ik had wel opgeschreven wat de computer als antwoord gaf, het waren er twee:
Of
De computer genereert telkens een andere vraag en die vraag heb ik niet meer voor mijn neus. Maar ik zal wel de manier waarop je je antwoorden hebt geschreven eens gaan gebruiken als ik weer zo'n vraag krijg.
Het is een zomercursus van de HvA en ik heb ook een boek HTO basisvaardigheden wiskunde (2e herziene druk ISBN: 978-90-01-76438-8) van Noordhoff Uitgevers. Maar ik leer niet uit het boek, ik oefen, nadat de docent uitleg heeft gegeven, op de computer omdat die vragen ook worden gesteld tijdens de toets.
Riparius heeft het antwoord al gegeven, waarom ligt een top op (p, q) bij een functie a(x-p)2 + q, wat is vereenvoudigen precies? Hoe vereenvoudig ik? Wat zijn de zogenaamde 'rekenregels', waarom werken deze zo? Het maakt het allemaal zoveel simpeler dan jezelf killen met vraagstukken zonder ze te begrijpen.
[ Bericht 0% gewijzigd door #ANONIEM op 16-06-2012 19:25:48 ]


Ik heb een opgave over bodeplot met uitwerkingen en heb hem uitgewerkt hoe ik denk dat het zou moeten maar een aantal zaken begrijp ik niet, en heb er een vraag bijgezet.
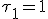 ,
, 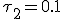 ,
, 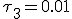 en
en 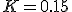 .
.
Asymptoten:
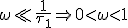 ,
, 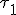 ,
, 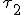 en
en 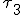 kunnen verwaarloosd worden dus:
kunnen verwaarloosd worden dus:
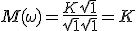
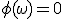
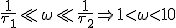 ,
, 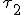 en
en 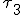 kunnen verwaarloosd worden dus:
kunnen verwaarloosd worden dus:
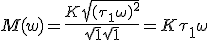
Vraag waarom kan de 1 die in de wortel staat in de teller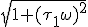 verwaarloosd worden?
verwaarloosd worden?
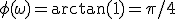
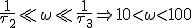 ,
, 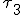 kan verwaarloosd worden dus:
kan verwaarloosd worden dus:
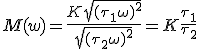
Vraag opnieuw waarom kan de 1 in de wortels verwaarloosd worden?
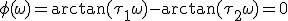
Vraag wanneer ik nu gewoon de getalletjes invul... dan krijg je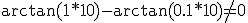 dus waarom is het 0? De enigste manier waarmee ik op 0 uitkom is dus met
dus waarom is het 0? De enigste manier waarmee ik op 0 uitkom is dus met 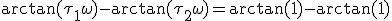
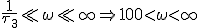 , alle termen doen nu mee.
, alle termen doen nu mee.
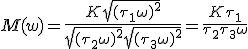
Vraag opnieuw waarom heeft de 1 in de wortel geen belang
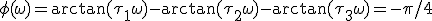
Zelfde hier... moet het niet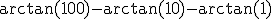 zijn?
zijn?
Asymptoten:
Vraag waarom kan de 1 die in de wortel staat in de teller
Vraag opnieuw waarom kan de 1 in de wortels verwaarloosd worden?
Vraag wanneer ik nu gewoon de getalletjes invul... dan krijg je
Vraag opnieuw waarom heeft de 1 in de wortel geen belang
Zelfde hier... moet het niet


Oke kan hem dus verwaarlozen. Zou je het misschien in woorden kunnen uitleggen. Ik heb die big-O notatie nooit begrepenquote:


Even kijken... Heb het nog ergens staan:quote:Op zondag 17 juni 2012 22:06 schreef Dale. het volgende:
[..]
Oke kan hem dus verwaarlozen. Zou je het misschien in woorden kunnen uitleggen. Ik heb die big-O notatie nooit begrepenen hoe zit het met
?
met O(g(n)) bedoelt men de verzameling functies f(n) zodat er positieve constanten c en n0 bestaan zodat:
voor alle
Dus, als f(n) = O(g(n)) bedoelt men dat vanaf een bepaalde waarde voor n (n0) de functie f(n) vanaf bovenaf begrensd wordt door een constante c maal de functie g.
Je kan f(n) = O(g(n)) dus intuïtief lezen als: f wordt begrensd door g(n).
Waarbij je natuurlijk wel in je achterhoofd moet houden dat je g maal een constante mag doen, en het alleen voor waarden van n hoeft te gelden die hoog genoeg zijn (n groter of gelijk aan n0)
Voorbeelden:
1/n = O(1)
(Want voor n groter of gelijk aan 1, geldt dat 1/n kleiner is dan 1. Natuurlijk kan je ook andere waarden dan c = 1 kiezen dan ik hier heb gedaan, het gaat erom dat deze waarden bestaan, niet welke waarden je precies kiest. Ik zou ook c = 1000 kunnen kiezen, en n0 = 100, want voor n groter dan of gelijk aan 100 geldt dat 1/n is minder of gelijk aan 1000)
[ Bericht 5% gewijzigd door kutkloon7 op 17-06-2012 23:05:56 ]


nevermind komt wel goed.
[ Bericht 49% gewijzigd door GoodGawd op 18-06-2012 13:05:52 ]
[ Bericht 49% gewijzigd door GoodGawd op 18-06-2012 13:05:52 ]
Blues ain't nothing but a good man feeling bad...


Je moet een particuliere oplossing vinden en de homogene vgl oplossen. Algemene oplossing is dan particulier + homogeen. En bedoel je daar een lambda?quote:Op maandag 18 juni 2012 12:58 schreef GoodGawd het volgende:
Vraagje, als ik de differntial equation heb:
y'' - 2y'- 3y = 3e2t
En ze vragen de general solution moet ik dit dan met dmv particular solution methode oplossen. Want dit is een niet homogene equation right.
Bij een homogene bijv:
y'' - 2y'- 3y = 0
kan ik gewoon de y subtitueren met (omgekeerde gamma, hoe heet dat tekentje ook alweer lol .... ) en dan verder oplossen spreek voor zich.


Ik weet niet zeker of dit het juiste topic is, maar:
aantal doelpunten / frequentie
0 / 31
1 / 64
2 / 83
3 / 55
4 / 27
5 / 18
6 / 16
7 / 9
8 / 3
Hier moet ik dus een boxplot bij maken. De totale frequentie is 306. Ik heb dat de mediaan het 153e + 154e getal, :2 is. Dus dan is de mediaan 2. Alleen dan moet je Q1 en Q3 berekenen, en dan snap ik het niet meer..
Iemand die me zou kunnen helpen?
aantal doelpunten / frequentie
0 / 31
1 / 64
2 / 83
3 / 55
4 / 27
5 / 18
6 / 16
7 / 9
8 / 3
Hier moet ik dus een boxplot bij maken. De totale frequentie is 306. Ik heb dat de mediaan het 153e + 154e getal, :2 is. Dus dan is de mediaan 2. Alleen dan moet je Q1 en Q3 berekenen, en dan snap ik het niet meer..
Iemand die me zou kunnen helpen?


Q1 en Q3 liggen ieder op een kwart van de getallenverzameling. Ze heten ook wel kwartielen. Vervolgens construeer je de boxplot door een doosje om Q1 en Q3 te tekenen in een geschikt stelsel, je geeft de meridiaan aan met een verticaal streepje en tekent de uitschieters naar het minimum en maximum.
[ Bericht 51% gewijzigd door #ANONIEM op 18-06-2012 21:26:34 ]
[ Bericht 51% gewijzigd door #ANONIEM op 18-06-2012 21:26:34 ]


Heb je al bedacht wat je voor je mondelinge presentatie gaat doen? Ik ontdekte vandaag dat je lang geleden een vraag hebt gesteld die relevant is voor de meetkundige interpretatie van de Weierstraß substitutie, maar dat je toen niets met mijn hint hebt gedaan.quote:Op maandag 18 juni 2012 21:23 schreef Amoeba het volgende:
Q1 en Q3 liggen ieder op een kwart van de getallenverzameling. Ze heten ook wel kwartielen.


Ik heb de Mercatorprojectie voorbereid, toevallig dat ik vandaag tijdens Nederlands me aan het inlezen was over bovengenoemde persoon, maar van die poging kwam niet veel terecht. Ik heb een felle discussie met mijn docenten wiskunde B gehad, misschien dat jij het antwoord weet?quote:Op maandag 18 juni 2012 21:30 schreef Riparius het volgende:
[..]
Heb je al bedacht wat je voor je mondelinge presentatie gaat doen? Ik ontdekte vandaag dat je lang geleden een vraag hebt gesteld die relevant is voor de meetkundige interpretatie van de Weierstraß substitutie, maar dat je toen niets met mijn hint hebt gedaan.
Ik heb als keuzeonderwerp de voortgezette integraalrekening, een K(euze)-onderwerp in deel 3 van Getal en Ruimte. Mijn ene docent motiveerde mij om die klok te maken, en raadde het af daarnaast een aanvullende presentatie over de Mercatorprojectie te geven, mijn andere docent was juist niet gecharmeerd van die klok, maar vond dat stukje verdieping wel een goed idee. Wat vinden de examinatoren nou goed?
Ik kan me die post met 3 linkjes nog heel goed herinneren.
Maar zo'n examen duurt 40 minuten, waarin een casus, een keuzeonderwerp en de rest behandeld moet worden..
[ Bericht 1% gewijzigd door #ANONIEM op 18-06-2012 21:41:09 ]


Tja, dat is niet zozeer een wiskundige vraag, maar meer dat je advies wil hebben. Ik begrijp wel dat de eerste docent(e) het afraadt om nog iets over de Mercatorprojectie te vertellen als je toch al de klok gaat doen (is dat soms een idee van hem/haar?) omdat het dan bij elkaar gewoon te veel wordt. De tijd gaat altijd veel sneller voorbij dan je denkt als je een presentatie doet waar het erg op de details aankomt.quote:Op maandag 18 juni 2012 21:38 schreef Amoeba het volgende:
[..]
Ik heb de Mercatorprojectie voorbereid, toevallig dat ik vandaag tijdens Nederlands me aan het inlezen was over bovengenoemde persoon, maar van die poging kwam niet veel terecht. Ik heb een felle discussie met mijn docenten wiskunde B gehad, misschien dat jij het antwoord weet?
Ik heb als keuzeonderwerp de voortgezette integraalrekening, een K(euze)-onderwerp in deel 3 van Getal en Ruimte. Mijn ene docent motiveerde mij om die klok te maken, en raadde het af daarnaast een aanvullende presentatie over de Mercatorprojectie te geven, mijn andere docent was juist niet gecharmeerd van die klok, maar vond dat stukje verdieping wel een goed idee. Wat vinden de examinatoren nou goed?
Zelf zit ik meer op de lijn van de tweede docent(e), die een stukje verdieping belangrijker vindt dan de uiterlijke vormgeving van je presentatie (de klok).
Ik doelde op een post van lang geleden, uit oktober 2011 om precies te zijn. Ben je waarschijnlijk al lang weer vergeten, maar ik niet, omdat ik het zo'n gemiste kans vond.quote:Ik kan me die post met 3 linkjes nog heel goed herinneren.(Gudermann functie zat er ook bij)
Hoeveel tijd krijg je voor je presentatie? En zijn je klasgenoten er dan ook bij als je je verhaal houdt, of gebeurt dat in besloten kring met alleen de examinatoren?quote:Maar zo'n examen duurt 40 minuten, waarin een casus, een keuzeonderwerp en de rest behandeld moet worden..


Ter verduidelijking, ik doe staatsexamen. Ik moet voor ieder vak slechts een schriftelijk en mondeling examen afleggen, schoolexamens doen we niet aan. M.u.v. bepaalde examens, zo zijn wiskunde D en maatschappijleer enkel mondeling.
Het betreft dus een onderonsje tussen mij en 2 examinatoren. Ik hoop voor die presentatie 10 minuten te krijgen. Ik wil ook niet zoveel met die klok doen, maar direct toestemming vragen om die presentatie te houden. Maar ik moest een werkstuk daarover maken, dus het is aan de gratie van mijn examinatoren.
Maargoed, J. is mijn docent, hij kwam met het idee v/d klok, inderdaad. Toen ik dat hier neerzette kwam jij met dat stukje verdieping, waar J. niet zo van gecharmeerd was, maar M., een eerstegraads docent wel.
En een quote van die post zou gewenst zijn.
[ Bericht 3% gewijzigd door #ANONIEM op 18-06-2012 22:01:48 ]
Het betreft dus een onderonsje tussen mij en 2 examinatoren. Ik hoop voor die presentatie 10 minuten te krijgen. Ik wil ook niet zoveel met die klok doen, maar direct toestemming vragen om die presentatie te houden. Maar ik moest een werkstuk daarover maken, dus het is aan de gratie van mijn examinatoren.
Maargoed, J. is mijn docent, hij kwam met het idee v/d klok, inderdaad. Toen ik dat hier neerzette kwam jij met dat stukje verdieping, waar J. niet zo van gecharmeerd was, maar M., een eerstegraads docent wel.
En een quote van die post zou gewenst zijn.
[ Bericht 3% gewijzigd door #ANONIEM op 18-06-2012 22:01:48 ]


Waarschijnlijk snapt die ene docent geen bal van projecties.quote:Op maandag 18 juni 2012 21:59 schreef Amoeba het volgende:
Ter verduidelijking, ik doe staatsexamen. Ik moet voor ieder vak slechts een schriftelijk en mondeling examen afleggen, schoolexamens doen we niet aan. M.u.v. bepaalde examens, zo zijn wiskunde D en maatschappijleer enkel mondeling.
Het betreft dus een onderonsje tussen mij en 2 examinatoren. Ik hoop voor die presentatie 10 minuten te krijgen. Ik wil ook niet zoveel met die klok doen, maar direct toestemming vragen om die presentatie te houden. Maar ik moest een werkstuk daarover maken, dus het is aan de gratie van mijn examinatoren.
Maargoed, J. is mijn docent, hij kwam met het idee v/d klok, inderdaad. Toen ik dat hier neerzette kwam jij met dat stukje verdieping, waar J. niet zo van gecharmeerd was, maar M., een eerstegraads docent wel.
En een quote van die post zou gewenst zijn.


Ah zo. Die andere docent is misschien bang dat hij het zelf niet meer gemakkelijk kan volgen, of alleen na er zelf extra moeite voor te hebben gedaan waar hij wellicht geen zin in heeft? Of denkt die docent wellicht dat je het niet goed aankunt? Je neemt natuurlijk wel een zeker risico als je iets gaat presenteren wat voor jezelf ook nieuw is. Je moet dan wel sterk in je schoenen staan en je onderwerp goed beheersen, zodat je geen onzekere indruk maakt tijdens het examen en eventuele 'lastige' vragen ook goed kunt beantwoorden.quote:Op maandag 18 juni 2012 21:59 schreef Amoeba het volgende:
Ter verduidelijking, ik doe staatsexamen. Ik moet voor ieder vak slechts een schriftelijk en mondeling examen afleggen, schoolexamens doen we niet aan. M.u.v. bepaalde examens, zo zijn wiskunde D en maatschappijleer enkel mondeling.
Het betreft dus een onderonsje tussen mij en 2 examinatoren. Ik hoop voor die presentatie 10 minuten te krijgen. Ik wil ook niet zoveel met die klok doen, maar direct toestemming vragen om die presentatie te houden. Maar ik moest een werkstuk daarover maken, dus het is aan de gratie van mijn examinatoren.
Maargoed, J. is mijn docent, hij kwam met het idee v/d klok, inderdaad. Toen ik dat hier neerzette kwam jij met dat stukje verdieping, waar J. niet zo van gecharmeerd was, maar M., een eerstegraads docent wel.
Ik doelde op deze post. Wellicht vraag je je nu af wat dit met de Weierstraß substitutie te maken kan hebben, maar om dat te begrijpen zou je dit en dit eens door kunnen nemen. Ik gaf destijds pythagoreïsche tripletten als hint, maar daar reageerde niemand op. Het verband is uiteraard dat de Weierstraß substitutie een rationale parametrisatie van de eenheidscirkel geeft en dat er oneindig veel punten met rationale coördinaten op de eenheidscirkel liggen die corresponderen met pythagoreïsche tripletten (a,b,c), aangezien uit a2 + b2 = c2 volgt dat (a/c)2 + (b/c)2 = 1, zodat de punten (a/c;b/c), (-a/c;b/c), (-a/c;-b/c), (a/c;-b/c) met rationale coördinaten op de eenheidscirkel liggen. Als je meer wil weten over dit laatste zou je p. 152-155 van dit boek eens door kunnen nemen.quote:En een quote van die post zou gewenst zijn.
[ Bericht 0% gewijzigd door Riparius op 19-06-2012 01:49:01 ]


Ik krijg de laatste tijd wel steeds vaker te horen dat hij geen tijd meer wil besteden aan de verdieping die ik zoek. Hij vertikte het ook al om mijn presentatie over de Mercatorprojectie een keer aan te horen, want een paar leerlingen hadden zijn hulp harder nodig. Die zitten pas in 4 havo, maar dat maakt blijkbaar niet uit tegenover een examenkandidaat.
Ik moest even denken waar dat vraagstuk vandaan kwam, maar het komt uit een webklas wiskunde over het ABC vermoeden van de UvA. Een goed geheugen schrijf ik je toe, trouwens.
Ik moest even denken waar dat vraagstuk vandaan kwam, maar het komt uit een webklas wiskunde over het ABC vermoeden van de UvA. Een goed geheugen schrijf ik je toe, trouwens.


Wat zouden een paar lastige vragen dan kunnen zijn? Ik verwacht dat de presentatie niet zo moeilijk zal zijn, zolang ik kan verdedigen dat we de integraal over de secans moeten evalueren voordat we de Mercatorprojectie kunnen realiseren heb ik een vrij goede presentatie (met in het achterhoofd dat het allemaal 'verdieping' is)
[ Bericht 50% gewijzigd door #ANONIEM op 18-06-2012 22:56:20 ]
[ Bericht 50% gewijzigd door #ANONIEM op 18-06-2012 22:56:20 ]


Als ik me even beperk tot de wiskundige aspecten (dus niet de historische of nautische aspecten) dan zou je bijvoorbeeld als vraag kunnen krijgen hoe je ½∙ln((1 + sin φ)/(1 - sin φ)) (met -½π < φ < ½π) goniometrisch herleidt tot ln(sec φ + tan φ) of tot ln(tan(π/4 + φ/2)).quote:Op maandag 18 juni 2012 22:37 schreef Amoeba het volgende:
Wat zouden een paar lastige vragen dan kunnen zijn? Ik verwacht dat de presentatie niet zo moeilijk zal zijn.


Ik kan de integraal over de secans uitschrijven en herleiden tot ln(secx + tanx) Vermenigvuldigen met 1 + sin phi, het kwadraat wegwerken (lnx^2 = 2lnx) en je bent al bijna klaar.quote:Op maandag 18 juni 2012 23:03 schreef Riparius het volgende:
[..]
Als ik me even beperk tot de wiskundige aspecten (dus niet de historische of nautische aspecten) dan zou je bijvoorbeeld als vraag kunnen krijgen hoe je ½∙ln((1 + sin φ)/(1 - sin φ)) (met -½π < φ < ½π) goniometrisch herleidt tot ln(sec φ + tan φ) of tot ln(tan(π/4 + φ/2)).
Met behulp van de formules van Simpson is het andere een keer gelukt, maar dat was slechts aantonen.
[ Bericht 5% gewijzigd door #ANONIEM op 18-06-2012 23:11:54 ]


Waarschijnlijk heeft die lerarenopleiding gedaan op het hbo. Dan schijn je echt niet meer te leren dan de standaard vwo stof. Echt slecht eigenlijk, want dan sta je niet/nauwelijks boven de stof. Maarja beter één leraar dan geen leraar....quote:Op maandag 18 juni 2012 22:25 schreef Amoeba het volgende:
Ik moet wel toegeven dat zodra ik buiten de stof van het vwo treed hij me nauwelijks kan volgen.


Hij is begonnen op de universiteit, maar is afgevallen naar een lerarenopleiding op het HBO inderdaad. Nou was zijn motivatie bij aanvang v/h schooljaar nog uitstekend, nu is het weinig meer waard.quote:Op maandag 18 juni 2012 23:25 schreef thenxero het volgende:
[..]
Waarschijnlijk heeft die lerarenopleiding gedaan op het hbo. Dan schijn je echt niet meer te leren dan de standaard vwo stof. Echt slecht eigenlijk, want dan sta je niet/nauwelijks boven de stof. Maarja beter één leraar dan geen leraar....


Dan zal het geen toppertje geweest zijnquote:Op maandag 18 juni 2012 23:28 schreef Amoeba het volgende:
[..]
Hij is begonnen op de universiteit, maar is afgevallen naar een lerarenopleiding op het HBO inderdaad. Nou was zijn motivatie bij aanvang v/h schooljaar nog uitstekend, nu is het weinig meer waard.
Dat je motivatie een beetje daalt als de zomervakantie nadert kan ik me wel voorstellen trouwens, had ik ook altijd als leerling op de middelbare school.


Nee. Hij kan wel duidelijk uitleggen, maar hij heeft blijkbaar de beperking dat vwo zijn beperking is. Ook wel wat meer, ik vroeg hem wat over hyperbolen en ellipsen construeren, daar kon hij ook wel mee uit de voeten.
Mijn motivatie neemt dan juist toe.
[ Bericht 25% gewijzigd door #ANONIEM op 18-06-2012 23:34:51 ]
Mijn motivatie neemt dan juist toe.
[ Bericht 25% gewijzigd door #ANONIEM op 18-06-2012 23:34:51 ]


Dat is toch ook gewoon standaard vwo stof? In ieder geval tot voor kort wel, dus wel logisch dat ie dat wel kan.


Wiskunde B niet meer, misschien wiskunde D.quote:Op maandag 18 juni 2012 23:35 schreef thenxero het volgende:
Dat is toch ook gewoon standaard vwo stof?
Ik denk dat Riparius op een uitzonderlijk lange verklarende post broedt
Maargoed, ik heb ooit een docente gehad die ik de tangens uit kon gaan leggen, dus het niveau is gestegen.
[ Bericht 11% gewijzigd door #ANONIEM op 18-06-2012 23:41:08 ]


Pff, en dat moet dan lesgevenquote:Op maandag 18 juni 2012 23:36 schreef Amoeba het volgende:
[..]
Wiskunde B niet meer, misschien wiskunde D.
Ik denk dat Riparius op een uitzonderlijk lange verklarende post broedt
Maargoed, ik heb ooit een docente gehad die ik de tangens uit kon gaan leggen, dus het niveau is gestegen.


Onderbouw havo/vwo. Gaf wiskunde, tekenen en geschiedenis. Bij geschiedenis ging zo voorlezen uit het tekstboek, bij wiskunde kwamen de vragen vaak bij mij terecht en tekenen had ik niet. Maar genoeg gehaat.


Daar heb ik eigenlijk even geen tijd voor. Ik vond nog wel twee artikelen waar je misschien wat aan hebt, hier en hier.quote:Op maandag 18 juni 2012 23:36 schreef Amoeba het volgende:
[..]
Wiskunde B niet meer, misschien wiskunde D.
Ik denk dat Riparius op een uitzonderlijk lange verklarende post broedt
Maar vooruit, even een leuk grapje dat ik zo gauw niet online vind om de Weierstraß substitutie af te leiden. We gaan uit van de volgende identiteit, die direct volgt met De Moivre:
(1) cos φ + i∙sin φ = (cos ½φ + i∙sin ½φ)2
Nu is ook:
(2) (cos ½φ + i∙sin ½φ) = 1/(cos ½φ - i∙sin ½φ),
zodat we voor (1) kunnen schrijven:
(3) cos φ + i∙sin φ = (cos ½φ + i∙sin ½φ)/(cos ½φ - i∙sin ½φ)
Teller en noemer van de breuk in het rechterlid van (3) delen door cos ½φ geeft dan:
(4) cos φ + i∙sin φ = (1 + i∙tan ½φ)/(1 - i∙tan ½φ)
Stellen we nu:
(5) t = tan ½φ,
dan is dus:
(6) cos φ + i∙sin φ = (1 + i∙t)/(1 - i∙t) = (1 - t2)/(1 + t2) + i∙2t/(1 + t2),
zodat:
(7) cos φ = (1 - t2)/(1 + t2) en sin φ = 2t/(1 + t2),
QED
[ Bericht 0% gewijzigd door Riparius op 20-06-2012 02:00:40 ]


Dat moet een zij-instromer zijn.quote:Maargoed, ik heb ooit een docente gehad die ik de tangens uit kon gaan leggen, dus het niveau is gestegen.
Het is te zot voor woorden. De stof van wiskunde B op VWO-niveau kan gemakkelijk in een half jaar worden gedoceerd (half jaar alleen dat) op HBO-niveau. Het is niet meer dan wat calculus en een klein beetje meetkunde. Hoe kan het dat bij een vierjarige HBO-opleiding voor leraar wiskunde nog geen 1/8ste wordt besteed aan het vak zelf. Natuurlijk is er ook wat pedagogie nodig maar die pedagogie moet relatief gezien de bijzaak zijn, de wiskunde de hoofdzaak. Verhoudingsgewijs zou minstens 3 jaar aan de wiskunde worden besteed en maximaal 1 jaar aan de pedagogie.quote:Waarschijnlijk heeft die lerarenopleiding gedaan op het hbo. Dan schijn je echt niet meer te leren dan de standaard vwo stof. Echt slecht eigenlijk, want dan sta je niet/nauwelijks boven de stof. Maarja beter één leraar dan geen leraar....
@Amoeba
Ik vind het een moedige keuze van jou om die mercatorprojectie te kiezen als onderwerp. Ik heb die artikelen oppervlakkig ingekeken, het is te volgen maar het vergt flink wat tijd en ik schat in dat je hier en daar nog wat kennis tekort komt. Je kiest zeker iets moeilijkers dan wat vereist is, dat is een goede instelling.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Het valt allemaal wel mee als je het eenmaal begrijpt. Als je Riparius zijn uitleg leest is het je voor 9/10de duidelijk, althans voor mij. Voor het mondeling examen moet je een onderwerp voorbereiden uit een lijstje, daarin staan o.a. de voortgezette integraalrekening (mijn keuze), complexe getallen, perspectief en nog wat onzin. Als presentatie van mijn keuzeonderwerp heb ik dus de Mercatorprojectie ( Het probleem van 1/cosφ primitiveren sluit daarbij aan (substitutiemethode & breuksplitsen)) voorbereid, maar de kans zit er ook in dat de examinatoren het niet eens aan willen horen..
@ Riparius:
Quite Easily Done
[ Bericht 7% gewijzigd door #ANONIEM op 19-06-2012 06:27:24 ]
@ Riparius:
Quite Easily Done
[ Bericht 7% gewijzigd door #ANONIEM op 19-06-2012 06:27:24 ]


Mijn proefpresentatie over die projectie ging slecht in het zesvoudige. Hoe krijg ik dit gepresenteerd in een snelle manier, ik krijg echt geen half uur.


Wiskunde tot in de details uitleggen kost altijd meer tijd dan je denkt... zeker als blijkt dat iedereen je wazig aankijkt tijdens je presentatie.
Je kan nog wat bezuinigen. Als je gebruikt dat x=y, kan je zeggen dat dit af te leiden is met xxxx. En dat je dat nog wel wil doen als ze dat graag willen zien, maar dat je dat omwille van de tijd even aanneemt.
Je kan nog wat bezuinigen. Als je gebruikt dat x=y, kan je zeggen dat dit af te leiden is met xxxx. En dat je dat nog wel wil doen als ze dat graag willen zien, maar dat je dat omwille van de tijd even aanneemt.


Dus is het makkelijk om de inleiding te geven, waarom we deze projectie willen, en dan direct door te gaan met het evalueren van de integraal?


Misschien nuttig om nog even op te merken dat je 1/cos φ op verschillende manieren in breuken kunt splitsen die zich eenvoudig laten primitiveren. Behalve de methode van Barrow, die neerkomt op:quote:Op dinsdag 19 juni 2012 06:19 schreef Amoeba het volgende:
Het valt allemaal wel mee als je het eenmaal begrijpt. Als je Riparius zijn uitleg leest is het je voor 9/10de duidelijk, althans voor mij. Voor het mondeling examen moet je een onderwerp voorbereiden uit een lijstje, daarin staan o.a. de voortgezette integraalrekening (mijn keuze), complexe getallen, perspectief en nog wat onzin. Als presentatie van mijn keuzeonderwerp heb ik dus de Mercatorprojectie ( Het probleem van 1/cosφ primitiveren sluit daarbij aan (substitutiemethode & breuksplitsen)) voorbereid, maar de kans zit er ook in dat de examinatoren het niet eens aan willen horen..
@ Riparius:
Quite Easily Done
sec φ = 1/cos φ = ½∙(cos φ/(1 + sin φ)) + ½∙(cos φ/(1 - sin φ)),
kun je ook nog gebuik maken van:
1 = cos2½φ + sin2½φ en cos φ = cos2½φ - sin2½φ,
zodat:
sec φ = 1/cos φ = (cos2½φ + sin2½φ)/(cos2½φ - sin2½φ),
waarbij we teller en noemer in het rechterlid kunnen delen door cos2½φ zodat we krijgen:
sec φ = 1/cos φ = (1 + tan2½φ)/(1 - tan2½φ) = ½∙(1 + tan2½φ)/(1 + tan ½φ) + ½∙(1 + tan2½φ)/(1 - tan ½φ),
en deze twee termen kun je weer gemakkelijk primitiveren aangezien ½∙(1 + tan2½φ) de afgeleide is van tan ½φ en dus ook van 1 + tan ½φ, oftewel d(1 + tan ½φ) = ½∙(1 + tan2½φ)∙dφ en daarmee ook -d(1 - tan ½φ) = ½∙(1 + tan2½φ)∙dφ. Dus heb je (voor -½π < φ < ½π):
∫ sec φ∙dφ = ∫ d(1 + tan ½φ)/(1 + tan ½φ) - ∫ d(1 - tan ½φ)/(1 - tan ½φ) = ln((1 + tan ½φ)/(1 - tan ½φ)) + C
En aangezien tan ¼π = 1 en tan(α + β) = (tan α + tan β)/(1 - tan α∙tan β) is uiteraard ook:
(1 + tan ½φ)/(1 - tan ½φ) = tan(¼π + ½φ)
Je kunt dit laatste resultaat ook verkrijgen en daarbij het gebruik van breuksplitsing geheel vermijden door 1/cos φ eerst te herschrijven als 1/sin(½π - φ) en dan pas de Weierstraß substitutie t = tan(½∙(½π - φ)) te gebruiken. Dan is namelijk 1/sin(½π - φ) = (1 + t2)/2t en dφ = -(2/(1 + t2))∙dt en krijg je dus heel eenvoudig:
∫ sec φ∙dφ = ∫ dφ/sin(½π - φ) = - ∫ dt/t = - ln t + C = - ln(tan(½∙(½π - φ))) + C = ln(tan(¼π + ½φ)) + C
[ Bericht 0% gewijzigd door Riparius op 20-06-2012 17:27:24 ]


Dat vind ik ook wel allemaal heel leuk. Ik begon helder, maar bij het definieren van de x-coördinaat raakte ik de draad kwijt, nou goed, dat is een kwestie van oefenen. Maar ik merk wel dat vooraleer het verhaal duidelijk is er al een kwartier verstreken is, en dan moet ik nog aan de integraal beginnen (wat de opzet van de hele presentatie is).


Dat zie je direct als je in de vergelijking met de twee breuken, die twee breuken bij elkaar optelt (noemers gelijk maken, etc).quote:Op woensdag 20 juni 2012 12:01 schreef Amoeba het volgende:
(cos(x))/((1-sin(x)) (1+sin(x)))
Waarom is dit gelijk aan ½ cosx/(1+sinx) + ½cosx/(1-sinx)?