SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Dat is correct.quote:Op maandag 21 mei 2012 08:21 schreef Don_Vanelli het volgende:
Het heeft me een uur van mn leven gekost, maar volgens mij is het antwoord dat de afstand tot de oorsprong gelijk is aan
Maar verklap nog maar niet hoe je het hebt gedaan, dan kan Amoeba nog even door puzzelen.


Ik moet toch uitkomen op een dikke gare wortel met 500x i? Of is dat te 'vereenvoudigen' tot 2cos4pi/9?quote:Op maandag 21 mei 2012 09:45 schreef Riparius het volgende:
[..]
Dat is correct.
Maar verklap nog maar niet hoe je het hebt gedaan, dan kan Amoeba nog even door puzzelen.


Je hebt twee complexe getallen m3 = -½ + i∙½√3 en n3 = -½ - i∙½√3 en je probleem is nu dat je van deze twee complexe getallen de derdemachtswortels moet bepalen. Maar dat is niet zuiver algebraïsch te doen en dat is precies waarop je stuk loopt.quote:Op maandag 21 mei 2012 09:57 schreef Amoeba het volgende:
[..]
Ik moet toch uitkomen op een dikke gare wortel met 500x i? Of is dat te 'vereenvoudigen' tot 2cos4pi/9?
De kubische vergelijking x3 - 3x + 1 = 0 die je op moet lossen heeft uitsluitend reële wortels, maar opmerkelijk genoeg zijn deze wortels met de formules van Cardano toch niet zonder complexe getallen uit te drukken. Daarom noemde men dit casus irreducibilis ('het onherleidbare geval').
Je kunt nu een paar dingen doen, namelijk verder werken met complexe getallen en gebruik maken van de formule van De Moivre, of zonder complexe getallen werken door een goniometrische substitutie in je oorspronkelijke kubische vergelijking uit te voeren.


Meh.
m3 = -1/2 - 1/2i√3
3*argz = 240 graden, dus arg z = 80 graden.
m = cos80 + i*sin80
n = 1/m
a = m+n
cos 80 + isin80 + 1/(cos80 + i*sin80)
[ Bericht 1% gewijzigd door #ANONIEM op 21-05-2012 10:12:58 ]
m3 = -1/2 - 1/2i√3
3*argz = 240 graden, dus arg z = 80 graden.
m = cos80 + i*sin80
n = 1/m
a = m+n
cos 80 + isin80 + 1/(cos80 + i*sin80)
[ Bericht 1% gewijzigd door #ANONIEM op 21-05-2012 10:12:58 ]


Inderdaad, daar komt het wel op neer, dat heb je snel gevonden (er zijn natuurlijk drie reële wortels, maar deze moet je hebben).quote:Op maandag 21 mei 2012 10:10 schreef Amoeba het volgende:
Meh.
m3 = -1/2 - 1/2i√3
3*argz = 240 graden, dus arg z = 80 graden.
m = cos80 + i*sin80
n = 1/m
a = m+n
cos 80 + isin80 + 1/(cos80 + i*sin80)
Als je nu nog ziet dat 1/(cos 80° + i*sin 80°) = cos 80° - i*sin80° (waarom?) dan ben je klaar.


(cos80 + i sin80)-1 = cos-80 + isin-80
cos-x = cosx
sin-x = -sinx
Gonio + De Moivre.
Maar even een vraagje uit nieuwsgierigheid, wat heb jij (allemaal) gestudeerd?
cos-x = cosx
sin-x = -sinx
Gonio + De Moivre.
Maar even een vraagje uit nieuwsgierigheid, wat heb jij (allemaal) gestudeerd?


Ah, je zit in mijn postgeschiedenis te kijken? Sorry, maar ik beantwoord geen privé vragen.quote:Op maandag 21 mei 2012 10:18 schreef Amoeba het volgende:
(cos80 + i sin80)-1 = cos-80 + isin-80
cos-x = cosx
sin-x = -sinx
Gonio + De Moivre.
Maar even een vraagje uit nieuwsgierigheid, wat heb jij (allemaal) gestudeerd?


Neen. Ik kwam toevallig je post tegen bij de vraag over dat gedicht van (Schrijver?), ik zie je regelmatig in DIG en hier. Sorry, ik was enkel benieuwd.quote:Op maandag 21 mei 2012 10:20 schreef Riparius het volgende:
[..]
Ah, je zit in mijn postgeschiedenis te kijken? Sorry, maar ik beantwoord geen privé vragen.
[ Bericht 0% gewijzigd door #ANONIEM op 21-05-2012 10:22:48 ]


Ohja, het volgens mij integreer ik nu een stuk van de bol waaruit nog een kegel ontbreekt. Dat zou je er wel weer bij op kunnen tellen: 1/3 pi r² h, met r=cos(p), h=sin(p). Dan krijg jequote:Op maandag 21 mei 2012 01:05 schreef Riparius het volgende:
[..]
Het lijkt erop alsof je hier het interval waarover je r neemt als constant beschouwt, maar dat is niet zo als je p varieert ...
Maar dat is nog steeds wat anders geloof ik, want dan krijg ik numeriek p=0.28.
[ Bericht 1% gewijzigd door thenxero op 21-05-2012 11:19:07 ]


Je maakt het allemaal veel te moeilijk met die drievoudige integraal, want eigenlijk maak je gebruik van het feit dat de oppervlakte van een cirkel met straal r gelijk is aan:quote:Op maandag 21 mei 2012 11:13 schreef thenxero het volgende:
[..]
Ohja, het volgens mij integreer ik nu een stuk van de bol waaruit nog een kegel ontbreekt. Dat zou je er wel weer bij op kunnen tellen
∫02π ∫0r ρdρdθ
Je kunt veel beter een enkelvoudige integraal met ϕ als variabele opstellen.
Ik krijg een beetje een punthoofd van WolframAlpha, want die wil mijn bolcoördinaten met (r,θ,ϕ) niet herkennen, dus ik heb me even moeten behelpen met f voor ϕ, maar de integraal die je zoekt is deze.
Maar goed, dat is alleen om even te laten zien wat je dan krijgt. Voor p = π/2 krijg je het volume van de halve bol, zijnde (2/3)∙π.
Eenvoudiger gaat het als volgt. Beschouw een snijvlak op een hoogte h vanaf het grondvlak van de halve bol en zij r de straal van de snijcirkel. Dan hebben we:
r = cos ϕ,
en:
h = sin ϕ,
dus ook:
dh = cos ϕ∙dϕ
Dit geeft voor de volumedifferentiaal dV:
dV = π∙r2∙dh = π∙cos3ϕ∙dϕ
En dus krijgen we voor het volume V met ϕ = p:
∫0p π∙cos3ϕ∙dϕ
Je kunt nu gemakkelijk in WolframAlpha nagaan (weer met f voor ϕ) dat dit precies hetzelfde resultaat oplevert als die onnodig lastige drievoudige integraal.
[ Bericht 5% gewijzigd door Riparius op 21-05-2012 13:03:29 ]


Nou ja, dilemma's, het is gewoon een opgave (uit het boek Beknopte Hoogere Algebra van Fred Schuh uit 1926, p. 287 als je het precies wil weten). Maar probeer eerst eens of je die kubische vergelijking op kunt lossen met een goniometrische substitutie, dus zonder gebruik van complexe getallen. Of kijk eens of je verder komt met de aanpak van thenxero.quote:Op maandag 21 mei 2012 12:56 schreef Amoeba het volgende:
Maargoed, heb je nog meer van zulke interessante dilemma's?
[ Bericht 0% gewijzigd door Riparius op 21-05-2012 13:20:33 ]


Ik heb er nog wel een voor jou als je wil? Maar hoe kon ik nou uitkomen op die oplossing van Wolframalpha, ofwel dat 'wortelantwoord'? Daar wil ik nog wel mee verder. Een zetje, gaarne.
[ Bericht 62% gewijzigd door #ANONIEM op 21-05-2012 13:32:53 ]
[ Bericht 62% gewijzigd door #ANONIEM op 21-05-2012 13:32:53 ]


Post hier maar. Als ik het niet weet op te lossen dan iemand anders wellicht wel. Is altijd leerzaam, ook voor de meelezers.quote:


Ja leuk, dan kan ik weer domme opmerkingen maken enzo.quote:Op maandag 21 mei 2012 13:33 schreef Riparius het volgende:
[..]
Post hier maar. Als ik het niet weet op te lossen dan iemand anders wellicht wel. Is altijd leerzaam, ook voor de meelezers.


Wat had je precies ingevoerd bij WolframAlpha?quote:Op maandag 21 mei 2012 13:30 schreef Amoeba het volgende:
Ik heb er nog wel een voor jou als je wil? Maar hoe kon ik nou uitkomen op die oplossing van Wolframalpha, ofwel dat 'wortelantwoord'? Daar wil ik nog wel mee verder. Een zetje, gaarne.


Goed, het gaat over een driehoek.
De oppervlakte O wordt gegeven door een functie:
O = sin(2a) + sin(a)√(21+4cos2(a))
Bereken exact de maximale waarde van O met behulp van differentieren. Met berekening gaarne, numeriek oplossen is te simpel.
Verder heb ik geen les gehad over bolcoördinaten en dubbele integralen, zoals gezegd: Buiten een CE Wiskunde B en 2 boeken Wiskunde D en een goede motivatie heb ik niet zo veel parate wiskundekennis.
De oppervlakte O wordt gegeven door een functie:
O = sin(2a) + sin(a)√(21+4cos2(a))
Bereken exact de maximale waarde van O met behulp van differentieren. Met berekening gaarne, numeriek oplossen is te simpel.
Verder heb ik geen les gehad over bolcoördinaten en dubbele integralen, zoals gezegd: Buiten een CE Wiskunde B en 2 boeken Wiskunde D en een goede motivatie heb ik niet zo veel parate wiskundekennis.


De kubische functie. Naar de exacte antwoorden gekeken, ofwel de middelste daarvan die op het gevraagde interval ligt.quote:Op maandag 21 mei 2012 13:37 schreef Riparius het volgende:
[..]
Wat had je precies ingevoerd bij WolframAlpha?


Als ik even kijk dan zie ik daar op het eerste gezicht geen interessant of elegant antwoord uitkomen, dus óf je hebt de opgave verkeerd overgenomen, óf ik mis iets.quote:Op maandag 21 mei 2012 13:38 schreef Amoeba het volgende:
Goed, het gaat over een driehoek.
De oppervlakte O wordt gegeven door een functie:
O = sin(2a) + sin(a)√(21+4cos2(a))
Bereken exact de maximale waarde van O met behulp van differentieren. Met berekening gaarne, numeriek oplossen is te simpel.


Je mist iets. Dit was een vraag op mijn proefwerk, om dit numeriek op te lossen. Maar zoals gegeven, eerst differentieren. De afgeleide moet 0 zijn.quote:Op maandag 21 mei 2012 13:51 schreef Riparius het volgende:
[..]
Als ik even kijk dan zie ik daar op het eerste gezicht geen interessant of elegant antwoord uitkomen, dus óf je hebt de opgave verkeerd overgenomen, óf ik mis iets.
Numeriek oplossen geeft O = 5. Dit gaf ons de drive om dit proberen exact te doen. Wat gelukt is.
[ Bericht 5% gewijzigd door #ANONIEM op 21-05-2012 13:57:37 ]


OK. Dit is gewoon wat je met de formule's van Cardano krijgt. Je had:quote:Op maandag 21 mei 2012 13:40 schreef Amoeba het volgende:
[..]
De kubische functie. Naar de exacte antwoorden gekeken, ofwel de middelste daarvan die op het gevraagde interval ligt.
m3 = -½ + i∙½√3 en n3 = -½ - i∙½√3
Elk van deze vergelijkingen heeft niet één maar drie oplossingen. Je krijgt dus 3 complexe getallen m1, m2, m3 en drie complexe getallen n1, n2, n3. Aangezien x = m + n kun je zo 9 combinaties maken, maar daarvan voldoen er maar 3, omdat je ook nog aan de voorwaarde mn = 1 moet voldoen.
Heb je één set oplossingen die voldoen, laten we zeggen m1 en n1 , dan kun je de twee andere waarden voor m en n vinden door te vermenigvuldigen met de beide primitieve derdemachts eenheidswortels, namelijk
ε1 = -½ + i∙½√3 en ε2 = -½ - i∙½√3
Aangezien ε1ε2 = 1 krijg je dan:
x1 = m1 + n1
x2 = ε1m1 + ε2n1
x3 = ε2m1 + ε1n1
Ik neem aan dat het nu wel wat duidelijker wordt hoe de uitdrukkingen die WolframAlpha geeft zijn opgebouwd.


Dan kom ik inderdaad ook uit op q³-3q+1=0 met q=sin(p)quote:Op maandag 21 mei 2012 12:35 schreef Riparius het volgende:
[..]
Je maakt het allemaal veel te moeilijk met die drievoudige integraal, want eigenlijk maak je gebruik van het feit dat de oppervlakte van een cirkel met straal r gelijk is aan:
∫02π ∫0r ρdρdθ
Je kunt veel beter een enkelvoudige integraal met ϕ als variabele opstellen.
Ik krijg een beetje een punthoofd van WolframAlpha, want die wil mijn bolcoördinaten met (r,θ,ϕ) niet herkennen, dus ik heb me even moeten behelpen met f voor ϕ, maar de integraal die je zoekt is deze.
Maar goed, dat is alleen om even te laten zien wat je dan krijgt. Voor p = π/2 krijg je het volume van de halve bol, zijnde (2/3)∙π.
Eenvoudiger gaat het als volgt. Beschouw een snijvlak op een hoogte h vanaf het grondvlak van de halve bol en zij r de straal van de snijcirkel. Dan hebben we:
r = cos ϕ,
en:
h = sin ϕ,
dus ook:
dh = cos ϕ∙dϕ
Dit geeft voor de volumedifferentiaal dV:
dV = π∙r2∙dh = π∙cos3ϕ∙dϕ
En dus krijgen we voor het volume V met ϕ = p:
∫0p π∙cos3ϕ∙dϕ
Je kunt nu gemakkelijk in WolframAlpha nagaan (weer met f voor ϕ) dat dit precies hetzelfde resultaat oplevert als die onnodig lastige drievoudige integraal.
Ik snap hoe je die enkele integraal bepaalt, maar ik snap niet wat er mis was met mijn redenatie en hoe jij aan de correcte drievoudige integraal bent gekomen (ik zie bijvoorbeeld de jacobiaan niet meer terug).
Ik beweer dat { (r,θ,ϕ) : 0<r<1, 0<θ<2pi, 0<ϕ<p } gelijk is aan de verzameling van de afgezaagde bovenhelft van de bol minus de kegel. Zie plaatje.


een wss heel domme vraag van mij hier:
hoe vereenvoudig je het volgende?
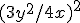 ?
? 
hoe vereenvoudig je het volgende?
Winnaar KLB verkiezingen 2012.

