[Bčta wiskunde] Huiswerk- en vragentopic

quote:

Op maandag 14 november 2011 13:06 schreef Dale. het volgende:

[..]

Euh sorry 1 regel geen idee waarom ik 2 regels schreef. Maar iig, het aantal combo's is 8844

Gewoon die-hard alle mogelijkheden doorgenomen?

Waarom wilde je dit berekenen trouwens?

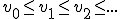V is een niet-lege , naar boven begrensde deelverzameling van . Ik wil een rij in V construeren zodat 1) en 2) sup V is de limiet van de rij.
Ik dacht zelf aan: construeer een rij zodat:


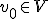
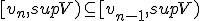
Ik heb nu moeite met het uitleggen dat sup V de limiet van de rij is. Ik dacht aan: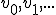 vormen het interval 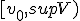waarvan ik wel kan bewijzen dat sup V het supremum is. Ook weet ik niet of het vanzelfsprekend is dat .
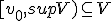Weet iemand hoe ik dit goed op kan schrijven? Of kan ik dit wel zo zeggen?

De rij met v_n=v₀ voldoet aan jouw constructie maar v₀ hoeft niet gelijk te zijn aan supV. Je kunt het bewijzen door onderscheid te maken tussen of supV in V zit.

quote:

Op zaterdag 19 november 2011 21:44 schreef Anoonumos het volgende:
V is een niet-lege , naar boven begrensde deelverzameling van . Ik wil een rij in V construeren zodat 1) en 2) sup V is de limiet van de rij.
Ik dacht zelf aan: construeer een rij zodat:


Ik heb nu moeite met het uitleggen dat sup V de limiet van de rij is.

Dat begrijp ik, omdat het gewoon niet klopt. Zie het tegenvoorbeeld van GlowMouse.

quote:

Ik dacht aan: vormen het interval waarvan ik wel kan bewijzen dat sup V het supremum is. Ook weet ik niet of het vanzelfsprekend is dat .
Weet iemand hoe ik dit goed op kan schrijven? Of kan ik dit wel zo zeggen?

Het is heel goed mogelijk dat sup(V) de limiet is van je rij terwijl sup(V) zelf niet in V zit.

Ja, stom. Het is gelukt.

quote:

Op zaterdag 19 november 2011 23:17 schreef Anoonumos het volgende:
Ja, stom. Het is gelukt.

Hoe dan?

quote:

Op zaterdag 19 november 2011 23:29 schreef thenxero het volgende:

[..]

Hoe dan?

1) sup V in V
Laat v0 = sup V. Construeer de rij v0 = v1 = v2 = ...
Deze rij heeft limiet sup V.
2) sup V niet in V. Laat v0 in V (Kan, V is niet leeg).
Sup V is een bovengrens van V. Voor elke vi in V geldt dus: (vi + supV)/2 < sup V, dus er is een v(i+1) in V met v(i + 1) > (vi + supV)/2. Construeer deze rij.
Sup V is de limiet van deze rij, want stel x is een kleinere bovengrens, dan:
(x+sup V)/2 < sup V dus er is een y in V met y > (x+supV)/2 > x. Tegenspraak.

quote:

Op zaterdag 19 november 2011 23:17 schreef Anoonumos het volgende:
Ja, stom. Het is gelukt.

Heb je er ook rekening mee gehouden dat je deelverzameling V van R geen interval hoeft te bevatten?

Je neemt dus v(i+1) = (v( i ) + sup V)/2, maar hoe weet je of die in je V zit? Misschien zitten er wel allemaal gaten in je verzameling.

Inderdaad niet volledig geformuleerd. Neem voor v(i+1) het kleinste element zo dat v(i + 1) > (vi + supV)/2. Zo had ik het bedacht.

quote:

Op zaterdag 19 november 2011 23:51 schreef Anoonumos het volgende:
Inderdaad niet volledig geformuleerd. Neem voor v(i+1) het kleinste element zo dat v(i + 1) > (vi + supV)/2. Zo had ik het bedacht.

Waarom bestaat dat element dan?

Een open verzameling in R heeft bijvoorbeeld geen kleinste element. Dus als je begint met v0 en
dan bestaat v1 al niet meer.

[ Bericht 18% gewijzigd door thenxero op 20-11-2011 00:01:15 ]

Heb je gelijk in. en anders weet ik het niet meer.

quote:

Op zaterdag 19 november 2011 23:53 schreef thenxero het volgende:

[..]

Een open verzameling in R heeft bijvoorbeeld geen kleinste element. Dus als je begint met v0 en
dan bestaat v1 al niet meer.

jawel

Als je zegt dat v(i+1) > vi en v(i+1) is bevat in V, is dat dan niet al voldoende voor een constructie?

quote:

Op zondag 20 november 2011 00:12 schreef Anoonumos het volgende:
Als je zegt dat v(i+1) > vi en v(i+1) is bevat in V, is dat dan niet al voldoende voor een constructie?

Nee, pak [0,1) en v_i = 0.5-1/i

quote:

Op zondag 20 november 2011 00:07 schreef GlowMouse het volgende:

[..]

jawel

?

quote:

Op zondag 20 november 2011 00:24 schreef thenxero het volgende:

[..]

?

never mind

quote:

Op zondag 20 november 2011 00:06 schreef Anoonumos het volgende:
Heb je gelijk in. en anders weet ik het niet meer.

Dat kan. Nu moet je alleen nog laten zien dat die verzameling niet leeg is, dus dat er daadwerkelijk zo'n v_{i+1} is en dat de limiet sup V is. (daarvoor moet je dus nog wel een extra eis hebben voor de keuze van v_{i+1}, anders kan de limiet ook kleiner dan de bovengrens zijn zoals Glowmouse al aangaf).

[ Bericht 4% gewijzigd door thenxero op 20-11-2011 00:37:31 ]

quote:

Op zondag 20 november 2011 00:06 schreef Anoonumos het volgende:
Heb je gelijk in. en anders weet ik het niet meer.

Dit gaat niet werken als je verzameling V slechts een eindig aantal elementen bevat (en dat kan).

quote:

Op zondag 20 november 2011 00:41 schreef Riparius het volgende:

[..]

Dit gaat niet werken als je verzameling V slechts een eindig aantal elementen bevat (en dat kan).

Is supV dan niet automatisch bevat in V? En daar had ik een simpele oplossing voor.
Bedankt voor de kritische blik allen.

quote:

Op zondag 20 november 2011 00:47 schreef Anoonumos het volgende:

[..]

Is supV dan niet automatisch bevat in V? En daar had ik een simpele oplossing voor.
Bedankt voor de kritische blik allen.

Precies dan is er geen probleem. Het lastige geval is als de sup buiten V ligt.

quote:

Op zondag 20 november 2011 00:47 schreef Anoonumos het volgende:

[..]

Is supV dan niet automatisch bevat in V? En daar had ik een simpele oplossing voor.
Bedankt voor de kritische blik allen.

Ja, dat is waar. Maar je zou een constructie voor je rij {v_n} moeten kunnen aangeven onafhankelijk van de aard van V en onafhankelijk van de vraag of sup(V) nu wel of geen element van V is, anders blijft het erg onelegant.

Hallo,

Gegeven is:
f(x) =
{ greatest integer function als x >= 0
{ least integer function als x < 0

Teken hiervan de grafiek, en beantwoord de vraag: "Why is f(x) called the integer part of x?"

---------------------------------

De grafiek tekenen is geen probleem, maar bij het beantwoorden van de vraag had ik in eerste instantie:
Mijn definitie 1: "f(x) is called the integer part of x, omdat de uitkomst ltijd een integer is voor elke waarde van x die je invult".

Echter, een andere definitie die ik kan geven (en die ik beter vind) is:
Mijn definitie 2: "stel ik vul x=2.14 in, dan is de uitkomst f(2.14) = 2. En voor x = -3.5 is de uitkomst f(-3.5) = -3. Dus f(x) is het integer gedeelte van x."

Het antwoord van het boek zegt:
Antwoord boek: "f(x) is called the integer part of x, becase |f(x)| is the largest integer that does not exceed x; i.e. |x| = |f(x)| + y, where 0 <= y < 1."

Ik heb moeite om het antwoord van het boek te begrijpen. Verder vind ik mijn definitie 2 beter dan definitie 1, maar is definitie 2 hetzelfde als het antwoord van het boek, maar dan anders geformuleerd?

M.a.w.; kan iemand mij het antwoord van het boek uitleggen, en aangeven of 'mijn definitie 2' hetzelfde qua betekenis is als het antwoord van het boek?

Bij voorbaat dank.

(p38 opg.32) -> Alle lezers: neger dit, dit is voor mijn eigen referentie

quote:

Op zondag 20 november 2011 14:26 schreef NonameNogame het volgende:
Hallo,
[...]
Bij voorbaat dank.

Het probleem met jouw definitie 2 is dat het een voorbeeld is. Je kan een voorbeeld geven van een definitie, maar de definitie zelf kan geen voorbeeld zijn. In plaats van die 2.14 en -3.5 moet je dus een algemene x>0 en x<0 nemen.

Wat er met integer part van een getal x bedoeld wordt is het "gehele gedeelte" van dat getal. Dat is dus het grootste gehele getal dat kleiner of gelijk is aan x.

Als x>0, dan geldt dus . Dus voor een geldt dan . Die y kan nooit groter dan 1 zijn, want dan is f(x) niet meer het grootste gehele getal kleiner dan of gelijk aan x. Dus . Probeer het nu zelf voor getallen x<0.


Oja, en definitie 1 is niet volledig. Als je de functie zou nemen f(x)=1 heb je ook een functie die altijd een geheel getal geeft voor iedere x. Maar dat is niet wat er bedoeld wordt met de "integer part of x".

[ Bericht 7% gewijzigd door thenxero op 20-11-2011 14:50:42 ]

Beste thenxero,

Bedankt voor je hulp, echter, ik heb nog steeds moeite om het te begrijpen.

Ik snap dat bij x >= 0, dat f(x) <= x moet zijn, want bij x >= 0 geldt de greatest integer function (zoals gegeven in de opgave).
Zo ook begrij ik dat bij x < 0, dat f(x) >= x moet zijn, want bij x < 0 geldt weer de least integer function (wederom gegeven in de opgave).

Met enkele voorbeelden en waarden:
x >= 0 (greatest integer function) ........... dus f(x) <= x...................bv: x = 2.5, dan f(x) = 2.
x < 0 (least integer function)................... dus f(x) >= x...................bv: x = -3.5, dan f(x) = -3.

Dit is ook makkelijk te zien in de grafiek die ik moest schetsen.

Maar stel nu (wederom een voorbeeld):
voor x >= 0 ............. dus f(x) <=x.............. en x = y + f(x) met 0 <= y < 1. Stel ik vul voor y = 0.9 in (voldoet aan 0 <= y < 1) en voor x = 2.5. Dan krijg ik:
x = y + f(x) voor x >=0 waarbij geldt dat f(x) <= x, en met waardes wordt deze:
2.5 = 0.9 + 2, maar dit klopt toch niet meer, want als ik de 0.9 'naar links breng', krijg ik:
1.6 = 2 ????

Ik raak volledig in de war zodra de y bijgehaald wordt. Als ik waardes in vul, kom ik er niet uit. Hier raak ik dan ook in de knoop