SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Een vraag uit een oefententamen:
Alvast dank!
Mijn antwoord:quote:Let S = [-1, 1] x [-1, 1] and C = { (x, y) | x2 + y2 <= 1 }.
Prove that |C| = |S|.
Hoe noteer ik dit eerste verhaal, over de bijectie, kort en duidelijk? Of moet ik gewoon dit verhaal uitleggen?quote:De eerste set kan je zien als alle elementen binnen of op de rand van een vierkant, de tweede set als alle elementen binnen of op de rand van een cirkel (waarschijnlijk hebben ze daarom ook C en S als letters voor de verzamelingen gekozen).
Ik zie dat er een injectieve functie bestaat van S naar C en omgekeerd. Van S naar C: Definieer r als (.5 + s1 / 2) waar s1 het eerste element uit het tupel uit S is, en a als (pi * s2 + pi) waar s2 het tweede element uit het tupel uit S is. Het bijbehorende tupel uit C is dan (r*cos(a), r*sin(a)).
De injectieve functie van C naar S is. (arctan2(c1, c2), sqrt(c12 + x22)) met c1 het eerste element uit het tupel uit C en c2 het tweede element uit het tupel uit C.
En omdat er een injectieve functie van C naar S is en andersom, geldt:
|C| <= |S|
|S| <= |C|
en volgens het theorem van Cantor-Schroeder-Bernstein ook:
|C| = |S|
Alvast dank!
Finally, someone let me out of my cage


Het punt (-1,0) van het vierkant wordt op hetzelfde punt afgebeeld als het punt (-1,1) van het vierkant.
[ Bericht 1% gewijzigd door twaalf op 25-10-2011 16:42:28 ]
[ Bericht 1% gewijzigd door twaalf op 25-10-2011 16:42:28 ]


Oh crapquote:Op dinsdag 25 oktober 2011 16:32 schreef twaalf het volgende:
Het punt (-1,0) van het vierkant wordt op hetzelfde punt afgebeeld als het punt (-1,1) van het vierkant.
Finally, someone let me out of my cage


Ik snap het al, je mag stellen |C| <= |S| omdat elk tupel in C ook in S zit, en dan gebruik je (ik leg het even geometrisch uit) een geschaald vierkant (bijvoorbeeld: [-.5, 5]2) en gebruik je dat elk geordend tupel uit het geschaalde vierkant in de cirkel zit.
Maar hoe noteer je nou een concrete functie die als domein C heeft en als codomein S (of andersom, of nog meer in het algemeen een functie die twee verzameling geordende n-tupels met n > 1 op elkaar afbeeldt, om het maar even wiskundig uit te drukken ).
).
Maar hoe noteer je nou een concrete functie die als domein C heeft en als codomein S (of andersom, of nog meer in het algemeen een functie die twee verzameling geordende n-tupels met n > 1 op elkaar afbeeldt, om het maar even wiskundig uit te drukken
Finally, someone let me out of my cage


Het bereik is
De functie is injectief, want...
Het bereik is
De functie is injectief, want...


Kan iemand mij het nut van het berekenen van een limit van een functie uitleggen? Je bepaalt dus de waarde die een bepaalde functie nooit zal bereiken, maar wat heb je daar aan?


Of wel, als de functie continu is in dat punt. Limieten zijn heel belangrijk, bijvoorbeeld voor de afgeleide (waarbij de functie zelf continu moet zijn).quote:Op dinsdag 25 oktober 2011 18:48 schreef Burbujas het volgende:
Kan iemand mij het nut van het berekenen van een limit van een functie uitleggen? Je bepaalt dus de waarde die een bepaalde functie nooit zal bereiken
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


klein voorbeeldje:quote:Op dinsdag 25 oktober 2011 18:48 schreef Burbujas het volgende:
Kan iemand mij het nut van het berekenen van een limit van een functie uitleggen? Je bepaalt dus de waarde die een bepaalde functie nooit zal bereiken, maar wat heb je daar aan?
g(x) = sin(x) is een relatief lelijke functie
f(x) = x is een relatief makkelijke functie
als je de limiet x ->0 pakt van sin(x)/x kun je laten zien dat deze limiet gelijk is aan 1. Dit betekent dus dat sin(x) zich in de buurt van x=0 gedraagt als de functie f(x) = x en je dus voor kleine waarden van x kunt zeggen: sin(x) is ongeveer gelijk aan x.
Ander voorbeeld:
Asymptoten berekenen gaat met behulp van limieten.


Ik denk dat limieten wel het belangrijkst zijn voor differentiŰren, zoals glowmouse al noemde. De afgeleide van een functie is namelijk gedefinieerd als een limiet:
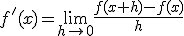


Als het goed is moet ik het doen via de epsilon-delta definitie.quote:Problem:
Let f, g: ℝ -> ℝ be continuous functions. Prove: For all α > 0 and β > 0, the function F: ℝ -> ℝ defined by F(x) = α * f(x) + β * g(x) is continuous.
Dit is wat ik tot nu toe heb:
Maar dat lijkt me dus veel te simpel. Pak ik het totaal verkeerd aan?quote:Because it is given that f(x) is continuous, it follows through the epsilon-delta definition that there exists a δ for which δ > |x-p| ≥ |f(x)-f(p)| holds. Then, it follows that δ * α > α * |x-p| ≥ α * |f(x)-f(p)|, which implies that f(x) * α is continuous if you choose α times the δ for which f(x) was continuous, as the δ for f(x) * α.
Ízil | Ki SY| Son HM| Lee SW| Taeguk Warriors|


Nee, dit gaat al verkeerd. Uit de ε,δ definitie van continu´teit volgt helemaal niet wat jij hier beweert. Als je functie f: R ↦ R continu is in x = p, dan bestaat er voor elke ε > 0 een δ > 0 zodanig dat | f(x) - f(p) | < ε voor elke x zodanig dat | x - p | < δ. Maar dat impliceert niet wat jij stelt.quote:Op woensdag 26 oktober 2011 03:25 schreef Thas het volgende:
[..]
Als het goed is moet ik het doen via de epsilon-delta definitie.
Dit is wat ik tot nu toe heb:
Because it is given that f(x) is continuous, it follows through the epsilon-delta definition that there exists a δ for which δ > |x-p| ≥ |f(x)-f(p)| holds.
[snip]


Ik zie het, jij hebt inderdaad de correcte, volledige definitie, ik maakte fouten.quote:Op woensdag 26 oktober 2011 04:04 schreef Riparius het volgende:
[..]
Nee, dit gaat al verkeerd. Uit de ε,δ definitie van continu´teit volgt helemaal niet wat jij hier beweert. Als je functie f: R ↦ R continu is in x = p, dan bestaat er voor elke ε > 0 een δ > 0 zodanig dat | f(x) - f(p) | < ε voor elke x zodanig dat | x - p | < δ. Maar dat impliceert niet wat jij stelt.
Als ik een simpele functie krijg als f(x)=sqrt(x) kan ik ook wel bewijzen of deze wel of niet continuous is in het punt P, door op zoek te gaan naar, zoals jij stelt, de δ waaruit blijkt dat |p - x| < δ impliceert dat |f(p) - f(x)| < ε waar gegeven is dat ε > 0 en δ > 0.
Ik probeer die methode nu op mijn probleem toe te passen. Mij lijkt het dan dat ik in dit geval de δ moet vinden waardoor δ > |p - x| impliceert dat ε > |f(p)*α-f(x)*α|, waar gegeven is dat ε > 0 en δ > 0.
En dan loop ik dus vast, omdat ik niet zou weten hoe ik die δ zou moeten vinden.
Ik kom niet verder dan |*f(x)-*f(p)|<|*f(p)-*f(p+δ)|
[ Bericht 1% gewijzigd door Thas op 26-10-2011 06:34:19 ]
Ízil | Ki SY| Son HM| Lee SW| Taeguk Warriors|


Je moet juist niet op zoek gaan naar de delta, maar naar de epsilon. Uiteindelijk moet je de som nemen van twee functies, en daar moet iets uitkomen dat kleiner is dan epsilon. Logisch is dan om te kijken naar 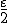 . Als je uitgaat van een bepaalde epsilon waaraan f+g moet voldoen, dan kun je voor
. Als je uitgaat van een bepaalde epsilon waaraan f+g moet voldoen, dan kun je voor 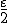 een
een 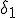 vinden voor f en een
vinden voor f en een 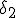 vinden voor g.
vinden voor g.


Vergeef mijn domheid, maar ik volg het niet helemaal (voorkennis slechts vwo Wiskunde A  ).
).
quote:Op dinsdag 25 oktober 2011 18:50 schreef GlowMouse het volgende:
[..]
Of wel, als de functie continu is in dat punt. Limieten zijn heel belangrijk, bijvoorbeeld voor de afgeleide (waarbij de functie zelf continu moet zijn).
Afgeleiden berekenen kan toch ook zonder je het limiet weet? (tenminste dat is hoe we op dit moment afgeleiden berekenen). En wat bedoel je met een functie die continu is?quote:Op dinsdag 25 oktober 2011 22:21 schreef thenxero het volgende:
Ik denk dat limieten wel het belangrijkst zijn voor differentiŰren, zoals glowmouse al noemde. De afgeleide van een functie is namelijk gedefinieerd als een limiet:
Dus door het limiet te bepalen kun je in sommige gevallen een ingewikkelde functie benaderen door dezelfde waarde in een simpelere functie in te vullen? Is dat het voordeel?quote:Op dinsdag 25 oktober 2011 19:45 schreef Don_Vanelli het volgende:
[..]
klein voorbeeldje:
g(x) = sin(x) is een relatief lelijke functie
f(x) = x is een relatief makkelijke functie
als je de limiet x ->0 pakt van sin(x)/x kun je laten zien dat deze limiet gelijk is aan 1. Dit betekent dus dat sin(x) zich in de buurt van x=0 gedraagt als de functie f(x) = x en je dus voor kleine waarden van x kunt zeggen: sin(x) is ongeveer gelijk aan x.
Ander voorbeeld:
Asymptoten berekenen gaat met behulp van limieten.


Het gaat er niet om dat je voor een 'gegeven' ε > 0 aantoont dat er zo'n δ is, maar dat je aantoont dat er voor elke ε > 0 een δ > 0 bestaat zodanig dat | f(x) - f(p) | < ε indien | x - p | < δ. Je moet dus een existentiebewijs leveren, en dat niet voor ÚÚn ε > 0 maar voor elke ε > 0. In het algemeen doe je dat door te laten zien dat je bij elke ε > 0 een δ > 0 kunt construeren die aan het gestelde voldoet.quote:Op woensdag 26 oktober 2011 04:33 schreef Thas het volgende:
[..]
Ik zie het, jij hebt inderdaad de correcte, volledige definitie, ik maakte fouten.
Als ik een simpele functie krijg als f(x)=sqrt(x) kan ik ook wel bewijzen of deze wel of niet continu is in het punt P, door op zoek te gaan naar, zoals jij stelt, de δ waaruit blijkt dat |x - p| < δ impliceert dat |f(p) - f(x)| < ε waar gegeven is dat ε > 0 en δ > 0.
Gegeven is dat f: R ↦ R en g: R ↦ R continue functies zijn. Gevraagd wordt nu te bewijzen dat de functie F: R ↦ R gedefinieerd door F(x) = α∙f(x) + β∙g(x) met α,β > 0 eveneens continu is op R.quote:[snip]
De continu´teit van f en g op R houdt in dat f en g continu zijn in elk punt op R. We kunnen daarom volstaan met aan te tonen dat de continu´teit van f en g voor een willekeurige x = p de continu´teit van F in x = p impliceert.
De continu´teit van f in x = p impliceert per definitie dat er voor elke εf > 0 een δf > 0 bestaat zodanig dat:
(1) | f(x) - f(p) | < εf voor | x - p | < δf
En de continu´teit van g in x = p impliceert evenzo dat er voor elke εg > 0 een δg > 0 bestaat zodanig dat:
(2) | g(x) - g(p) | < εg voor | x - p | < δg
We kiezen nu een willekeurige ε > 0 en kiezen dan vervolgens:
(3) εf = ε/2α en εg = ε/2β
Aangezien ε > 0 en tevens α,β > 0 volgt uit (3) dat ook εf > 0 en εg > 0. En dus bestaan er op grond van de continu´teit van f en g in x = p een δf > 0 en een δg > 0 waarmee voldaan wordt aan (1) resp. (2). Vermenigvuldiging van de leden van de eerste ongelijkheid in (1) met α resp. vermenigvuldiging van de leden van de eerste ongelijkheid in (2) met β levert nu dat geldt:
(4) | α∙f(x) - α∙f(p) | < α∙εf = ε/2 voor | x - p | < δf
En:
(5) | β∙g(x) - β∙g(p) | < β∙εg = ε/2 voor | x - p | < δg
Zij nu δ = min(δf,δg). Dan is δ ≤ δf en tevens δ ≤ δg zodat uit (4) en (5) volgt dat ook geldt:
(6) | α∙f(x) - α∙f(p) | < ε/2 voor | x - p | < δ
En:
(7) | β∙g(x) - β∙g(p) | < ε/2 voor | x - p | < δ
Optelling van de leden van de eerste ongelijkheden in (6) en(7) levert nu dat geldt:
(8) | α∙f(x) - α∙f(p) | + | β∙g(x) - β∙g(p) | < ε voor | x - p | < δ
En op grond van de driehoeksongelijkheid geldt ook:
(9) | (α∙f(x) + β∙g(x)) - (α∙f(p) + β∙g(p)) | ≤ | α∙f(x) - α∙f(p) | + | β∙g(x) - β∙g(p) |
Uit (8) en (9) alsmede F(x) = α∙f(x) + β∙g(x) volgt aldus dat:
(10) | F(x) - F(p) | < ε voor | x - p | < δ
Aangezien ε > 0 willekeurig was gekozen hebben we nu laten zien dat er voor elke ε > 0 een δ > 0 is te vinden waarmee aan (10) wordt voldaan, en dat betekent niets anders dan dat F continu is in x = p,
QED


Kun je een opgave mbt lineair programmeren ook makkelijk zonder grafieken oplossen?
Bij onderstaand voorbeeld kom ik ook tot de volgende regels:
Doelfunctie:
Maximaliseer: C = 5a + 4b
Voorwaarden:
Xeneen: 8a + 4b ≤ 16000
Ypreen: 2a + 6b ≤ 12000
Arbeid: 5a + 6b ≤ 15000
a ≥ 0
b ≥ 0
Echter lossen ze het daarna op met door middel van grafiekjes. Kan dit dus ook zonder grafiekjes?
Opgave: http://www.wiskundebijles(...)air_programmeren.htm
Bij onderstaand voorbeeld kom ik ook tot de volgende regels:
Doelfunctie:
Maximaliseer: C = 5a + 4b
Voorwaarden:
Xeneen: 8a + 4b ≤ 16000
Ypreen: 2a + 6b ≤ 12000
Arbeid: 5a + 6b ≤ 15000
a ≥ 0
b ≥ 0
Echter lossen ze het daarna op met door middel van grafiekjes. Kan dit dus ook zonder grafiekjes?
Opgave: http://www.wiskundebijles(...)air_programmeren.htm


http://nl.wikipedia.org/wiki/Simplexmethodequote:Op woensdag 26 oktober 2011 16:09 schreef GuitarJJ het volgende:
Kun je een opgave mbt lineair programmeren ook makkelijk zonder grafieken oplossen?
Bij onderstaand voorbeeld kom ik ook tot de volgende regels:
Doelfunctie:
Maximaliseer: C = 5a + 4b
Voorwaarden:
Xeneen: 8a + 4b ≤ 16000
Ypreen: 2a + 6b ≤ 12000
Arbeid: 5a + 6b ≤ 15000
a ≥ 0
b ≥ 0
Echter lossen ze het daarna op met door middel van grafiekjes. Kan dit dus ook zonder grafiekjes?
Opgave: http://www.wiskundebijles(...)air_programmeren.htm
edit: ik bekijk nu pas je link. Ze komen bij de a=1285.71 en b= 1428.57 door ook naar de figuur te kijken, anders weet je niet welke voorwaardevergelijkingen je moet oplossen. Hoe ze het in jouw link doen, heb je dus nog steeds de grafiekjes nodig. Het kan wel zonder, met het simplexalgoritme, maar dat is wel veel werk.
[ Bericht 12% gewijzigd door freiss op 26-10-2011 16:37:25 ]
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!


Maak er eens getallen van? Dus eerst de delingen doen, daarna pas de macht verheffen?
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


187 gedeeld door 555, dat is 0,3369 dat doe je vervolgens tot de macht 0,2 (is immers hetzelfde als 1/5) en voila 0,804


aight bedankt manquote:Op woensdag 26 oktober 2011 17:48 schreef Alfje het volgende:
187 gedeeld door 555, dat is 0,3369 dat doe je vervolgens tot de macht 0,2 (is immers hetzelfde als 1/5) en voila 0,804
kan ik verder met de berekening


Zoek de handleiding van je calculator eens op ...quote:Op woensdag 26 oktober 2011 17:45 schreef DeRakker. het volgende:
[ link | afbeelding ]
weten jullie hoe ik op het antwoord kom? ik kom steeds op andere getallen.
thx


Bedankt voor je reactie. Helaas dus geen simpele oplossing!quote:Op woensdag 26 oktober 2011 16:28 schreef freiss het volgende:
[..]
http://nl.wikipedia.org/wiki/Simplexmethode
edit: ik bekijk nu pas je link. Ze komen bij de a=1285.71 en b= 1428.57 door ook naar de figuur te kijken, anders weet je niet welke voorwaardevergelijkingen je moet oplossen. Hoe ze het in jouw link doen, heb je dus nog steeds de grafiekjes nodig. Het kan wel zonder, met het simplexalgoritme, maar dat is wel veel werk.

