SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Oh, je kunt niet zeggen dat het >= is, de stelling is dus niet waar.quote:Op donderdag 20 oktober 2011 20:08 schreef Physics het volgende:
Ik wilde eigenlijk alleen maar het eindantwoord ter controle
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Er staat kleiner of gelijk.quote:
[..]
Oh, je kunt niet zeggen dat het >= is, de stelling is dus niet waar.
Geldt hetzelfdequote:
De stelling kan best juist zijn, maar het hangt af van je keuze voor A, B, C en je kansmaat.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hallo allen, wiskundig gezien ben ik echt dyslectisch... Ik heb de volgende formule:
y = 0.8 [ y - (0.3 y + 20)] + 20 + 120 + 200 + [(208 - ( 0.2 y + 20)]
Nu staat er in het antwoordblad als volgende stap:
y = 0.8 [ y - (0.3 y + 20)] + 20 + 120 + 200 + 208 - 0.2 y - 20
Mijn vraag is, hoe kan je die haakjes zomaar weghalen? Waarom moet het niet uiteindelijk worden:
y = 0.8y - 0.24 y - 16 + 20 + 120 + 200 + 208 - 0.16 y - 16
y = 0.8 [ y - (0.3 y + 20)] + 20 + 120 + 200 + [(208 - ( 0.2 y + 20)]
Nu staat er in het antwoordblad als volgende stap:
y = 0.8 [ y - (0.3 y + 20)] + 20 + 120 + 200 + 208 - 0.2 y - 20
Mijn vraag is, hoe kan je die haakjes zomaar weghalen? Waarom moet het niet uiteindelijk worden:
y = 0.8y - 0.24 y - 16 + 20 + 120 + 200 + 208 - 0.16 y - 16
Het eerste deel van je antwoord klopt, alleen de laatste twee termen zijn fout. Je vermenigvuldigt ze met 0.8, maar je hoeft alleen [y - (0.3 y + 20)] met 0.8 te vermenigvuldigen.quote:
Hallo allen, wiskundig gezien ben ik echt dyslectisch... Ik heb de volgende formule:
y = 0.8 [ y - (0.3 y + 20)] + 20 + 120 + 200 + [(208 - ( 0.2 y + 20)]
Nu staat er in het antwoordblad als volgende stap:
y = 0.8 [ y - (0.3 y + 20)] + 20 + 120 + 200 + 208 - 0.2 y - 20
Mijn vraag is, hoe kan je die haakjes zomaar weghalen? Waarom moet het niet uiteindelijk worden:
y = 0.8y - 0.24 y - 16 + 20 + 120 + 200 + 208 - 0.16 y - 16
The biggest argument against democracy is a five minute discussion with the average voter.
Ik vind het wel apart dat je wel doorhebt dat je 20, 120, 200, 208 niet met 0.8 moet vermenigvuldigen maar dan wel die laatste term weer gaat vermenigvuldigen met 0.8.
oke, maar waarom wordt het bij die laatste term dan wel -20 en niet ook -280 ? Je haalt toch bij beide de haakjes weg?quote:
[..]
Het eerste deel van je antwoord klopt, alleen de laatste twee termen zijn fout. Je vermenigvuldigt ze met 0.8, maar je hoeft alleen [y - (0.3 y + 20)] met 0.8 te vermenigvuldigen.
hah, ja nu je het zegt. Ik heb dat soort dingen gewoon niet door. Wiskunde is echt niet mijn ding.quote:Op vrijdag 21 oktober 2011 19:32 schreef thenxero het volgende:
Ik vind het wel apart dat je wel doorhebt dat je 20, 120, 200, 208 niet met 0.8 moet vermenigvuldigen maar dan wel die laatste term weer gaat vermenigvuldigen met 0.8.
Waar haal je dan die extra - vandaan ? En je bedoelde zeker 208.quote:
[..]
oke, maar waarom wordt het bij die laatste term dan wel -20 en niet ook -280 ? Je haalt toch bij beide de haakjes weg?
[..]
hah, ja nu je het zegt. Ik heb dat soort dingen gewoon niet door. Wiskunde is echt niet mijn ding.
idd 208. Ik vat eigenlijk niet waarom je van +20 naar -20 gaat. Ik weet dat het te maken heeft met het weghalen van de haakjes, maar waarom veranderd het getal 20 dan van positief naar negatief en verandert 208 niet?quote:
[..]
Waar haal je dan die extra - vandaan ? En je bedoelde zeker 208.
Het minteken is dus van toepassing op alles binnen de ronde haakjes, niet alleen op 0.2y. Dat zorgt ervoor dat er -1*0.2y + -1*20 komt te staan als je de haakjes wegwerkt. Die +- wordt dan een -. Je krijgt ook een - als er -+ staat. Krijg je daarentegen ++ of - -, dan kun je dat vervangen door een +.quote:
[..]
idd 208. Ik vat eigenlijk niet waarom je van +20 naar -20 gaat. Ik weet dat het te maken heeft met het weghalen van de haakjes, maar waarom veranderd het getal 20 dan van positief naar negatief en verandert 208 niet?
-(a+b) = - a - b
Waarom?
-(a+b) = -1 * (a+b) = -1*a + -1*b = - a - b, waarbij we gebruik maken van de regel c(a+b) = ca + cb.
Waarom?
-(a+b) = -1 * (a+b) = -1*a + -1*b = - a - b, waarbij we gebruik maken van de regel c(a+b) = ca + cb.
. Bedankt mensen!
Luitjes,
Ik heb een klein probleempje. Ik moet de formule opstellen van dX + dY = f, waarbij d, e en f breuken zijn.
Een van de coördinaten is gegeven, (-1, 0)
Het andere punt ligt op deze lijn:
(x*, y*) moet rationaal zijn.
Als ik naar een simpele schets van mijn eenheidscirkel keek sprong x = 1/2 naar voren. Hieruit volgde dat y^2 = 3/4 dus y = 1/2√3
Tipje van de sluier graag
Ik heb een klein probleempje. Ik moet de formule opstellen van dX + dY = f, waarbij d, e en f breuken zijn.
Een van de coördinaten is gegeven, (-1, 0)
Het andere punt ligt op deze lijn:
(x*, y*) moet rationaal zijn.
Als ik naar een simpele schets van mijn eenheidscirkel keek sprong x = 1/2 naar voren. Hieruit volgde dat y^2 = 3/4 dus y = 1/2√3
Tipje van de sluier graag
Mag je in het plaatje gaan meten dan? Want dan snap ik niet echt het nut van deze opdrachtquote:
Luitjes,
Ik heb een klein probleempje. Ik moet de formule opstellen van dX + eY = f, waarbij d, e en f breuken zijn.
Een van de coördinaten is gegeven, (-1, 0)
Het andere punt ligt op deze lijn:
[ afbeelding ]
(x*, y*) moet rationaal zijn.
Als ik naar een simpele schets van mijn eenheidscirkel keek sprong x = 1/2 naar voren. Hieruit volgde dat y^2 = 3/4 dus y = 1/2√3
Tipje van de sluier graag
Beneath the gold, bitter steel
Nee. Maar het is wel duidelijk dat ik de waarden x = 1/2 en y = 1/2√ 3 diende te nemen.quote:
[..]
Mag je in het plaatje gaan meten dan? Want dan snap ik niet echt het nut van deze opdracht
Dus de bedoeling is gewoon een vergelijking voor de lijn door die 2 punten?
Beneath the gold, bitter steel
Ja, toch wel. Vraag fout gelezen vrees ik.quote:
Dus de bedoeling is gewoon een vergelijking voor de lijn door die 2 punten?
Mijn GR gaat dit probleempje eens bekijken.
Nou ten eerste is je tweede coordinaat niet helemaal correct, want je zit toch echt in de negatieve y-as...quote:
[..]
Ja, toch wel. Vraag fout gelezen vrees ik.
Mijn GR gaat dit probleempje eens bekijken.
Beneath the gold, bitter steel
Ik bedoel natuurlijk -.5sqrt(3).....quote:
[..]
Nou ten eerste is je tweede coordinaat niet helemaal correct, want je zit toch echt in de negatieve y-as...
Inderdaad. De vraagstelling van Amoeba is ook incompleet. Hij denkt kennelijk dat er maar één lijn is die aan het gestelde voldoet, maar dat is niet zo. Er liggen oneindig veel punten in ieder kwadrant op de eenheidscirkel waarvan de coördinaten rationaal zijn.quote:
[..]
y* moest toch rationaal zijn? In dat geval is y* dat zeker niet.
Ik moet een tegenvoorbeeld vinden voor
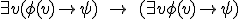
Ik moet zelf een taal L, structuur M en formules phi en psi bedenken zodat het niet klopt. Wie kan me helpen?
Ik moet zelf een taal L, structuur M en formules phi en psi bedenken zodat het niet klopt. Wie kan me helpen?
't Is een implicatie. Wanneer is deze niet waar?quote:
Ik moet een tegenvoorbeeld vinden voor
Ik moet zelf een taal L, structuur M en formules phi en psi bedenken zodat het niet klopt. Wie kan me helpen?
Als de linkerkant wel waar is en de rechterkant niet.quote:
[..]
't Is een implicatie. Wanneer is deze niet waar?
De rechterkant is ook weer een implicatie. Die moet dus niet waar zijn. Daaruit kun je wederom conclusies trekken.quote:
[..]
Als de linkerkant wel waar is en de rechterkant niet.
Ja... maar ik zoek eigenlijk een tegenvoorbeeld he.
Ik heb nu alle implicaties eruit gehaald maar ik zie niet hoe dat helpt:
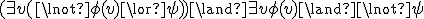
TeX kan hier blijkbaar niet alle logische symbolen weergeven.
[ Bericht 81% gewijzigd door thenxero op 24-10-2011 21:32:34 ]
Ik heb nu alle implicaties eruit gehaald maar ik zie niet hoe dat helpt:
TeX kan hier blijkbaar niet alle logische symbolen weergeven.
[ Bericht 81% gewijzigd door thenxero op 24-10-2011 21:32:34 ]
Een vraag uit een oefententamen:
Alvast dank!
Mijn antwoord:quote:Let S = [-1, 1] x [-1, 1] and C = { (x, y) | x2 + y2 <= 1 }.
Prove that |C| = |S|.
Hoe noteer ik dit eerste verhaal, over de bijectie, kort en duidelijk? Of moet ik gewoon dit verhaal uitleggen?quote:De eerste set kan je zien als alle elementen binnen of op de rand van een vierkant, de tweede set als alle elementen binnen of op de rand van een cirkel (waarschijnlijk hebben ze daarom ook C en S als letters voor de verzamelingen gekozen).
Ik zie dat er een injectieve functie bestaat van S naar C en omgekeerd. Van S naar C: Definieer r als (.5 + s1 / 2) waar s1 het eerste element uit het tupel uit S is, en a als (pi * s2 + pi) waar s2 het tweede element uit het tupel uit S is. Het bijbehorende tupel uit C is dan (r*cos(a), r*sin(a)).
De injectieve functie van C naar S is. (arctan2(c1, c2), sqrt(c12 + x22)) met c1 het eerste element uit het tupel uit C en c2 het tweede element uit het tupel uit C.
En omdat er een injectieve functie van C naar S is en andersom, geldt:
|C| <= |S|
|S| <= |C|
en volgens het theorem van Cantor-Schroeder-Bernstein ook:
|C| = |S|
Alvast dank!
Finally, someone let me out of my cage
Het punt (-1,0) van het vierkant wordt op hetzelfde punt afgebeeld als het punt (-1,1) van het vierkant.
[ Bericht 1% gewijzigd door twaalf op 25-10-2011 16:42:28 ]
[ Bericht 1% gewijzigd door twaalf op 25-10-2011 16:42:28 ]
Oh crapquote:
Het punt (-1,0) van het vierkant wordt op hetzelfde punt afgebeeld als het punt (-1,1) van het vierkant.
Finally, someone let me out of my cage
Ik snap het al, je mag stellen |C| <= |S| omdat elk tupel in C ook in S zit, en dan gebruik je (ik leg het even geometrisch uit) een geschaald vierkant (bijvoorbeeld: [-.5, 5]2) en gebruik je dat elk geordend tupel uit het geschaalde vierkant in de cirkel zit.
Maar hoe noteer je nou een concrete functie die als domein C heeft en als codomein S (of andersom, of nog meer in het algemeen een functie die twee verzameling geordende n-tupels met n > 1 op elkaar afbeeldt, om het maar even wiskundig uit te drukken).
Maar hoe noteer je nou een concrete functie die als domein C heeft en als codomein S (of andersom, of nog meer in het algemeen een functie die twee verzameling geordende n-tupels met n > 1 op elkaar afbeeldt, om het maar even wiskundig uit te drukken
).
Finally, someone let me out of my cage
