SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
In een aquarium staat het water 40 cm hoog. Het aquarium wordt leeggeheveld.
Na 10 min is het leeg.
Welke formule geeft het verband tussen de waterhoogte h in cm en de tijd t in minuten?
Na 10 min is het leeg.
Welke formule geeft het verband tussen de waterhoogte h in cm en de tijd t in minuten?
Het wordt leeggeheveld, dat lijkt me niet lineair te verlopen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
In dit geval wel.quote:Op zaterdag 8 oktober 2011 12:01 schreef GlowMouse het volgende:
Het wordt leeggeheveld, dat lijkt me niet lineair te verlopen.
Ah, je hebt gelijk.
Sorry, mijn fout.
Zo zie je maar weer dat ik niet bepaald de briljanste ben in wiskunde.
Edit : Geen dank !
Sorry, mijn fout.
Zo zie je maar weer dat ik niet bepaald de briljanste ben in wiskunde.
Edit : Geen dank !
Ik snap het, dank u!quote:
H = 40 - (4t)
Je startwaarde is 40 en het waterhoogte daalt met 40/10 = 4 cm per minuut,
leg even uit waarom de haakjes er staanquote:
Op
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
De haakjes staan er om ervoor te zorgen dat de vermenigvuldiging eerst plaatsvindt.
Indien je "40 - 4t" zou opschrijven, krijg je :
40 - 4 = 36 en dan
36 * t
Indien je "40 - 4t" zou opschrijven, krijg je :
40 - 4 = 36 en dan
36 * t
Ik kom niet uit de volgende limiet
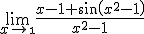
(x˛-1) = (x-1)(x+1), maar verder kom ik niet. Sin (a -b) = sin a cos a - cos a sin b leverde me niets op. L'hospital's rule ken ik niet. Kan iemand helpen?
(x˛-1) = (x-1)(x+1), maar verder kom ik niet. Sin (a -b) = sin a cos a - cos a sin b leverde me niets op. L'hospital's rule ken ik niet. Kan iemand helpen?
oj, zie http://www.khanacademy.or(...)t=Developmental+Mathquote:
De haakjes staan er om ervoor te zorgen dat de vermenigvuldiging eerst plaatsvindt.
Indien je "40 - 4t" zou opschrijven, krijg je :
40 - 4 = 36 en dan
36 * t
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
quote:
Ik kom niet uit de volgende limiet
(x˛-1) = (x-1)(x+1), maar verder kom ik niet. Sin (a -b) = sin a cos a - cos a sin b leverde me niets op. L'hospital's rule ken ik niet. Kan iemand helpen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oh ja.quote:
[..]
oj, zie http://www.khanacademy.or(...)t=Developmental+Math
Tja, dit bevestigt mijn eerdere stelling.
De kromme K bestaat uit alle punten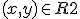 
die voldoen aan
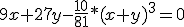
Deze kromme heeft een raaklijn L in het punt (0, 0).
(a) Geef de vergelijking van L in de vorm y = rx + b.
(b) Er zijn twee punten op K waar de raaklijnen zo zijn dat ze de lijn L
ergens loodrecht snijden. Bereken de co¨ordinaten van deze punten.
Met impliciet differentieren krijg ik bij a) L = -1/3 x.
Dus voor de andere raaklijn geldt helling = 3. Ik weet niet hoe ik nu x en y kan vinden.
[ Bericht 14% gewijzigd door Anoonumos op 08-10-2011 15:57:47 ]
Deze kromme heeft een raaklijn L in het punt (0, 0).
(a) Geef de vergelijking van L in de vorm y = rx + b.
(b) Er zijn twee punten op K waar de raaklijnen zo zijn dat ze de lijn L
ergens loodrecht snijden. Bereken de co¨ordinaten van deze punten.
Met impliciet differentieren krijg ik bij a) L = -1/3 x.
Dus voor de andere raaklijn geldt helling = 3. Ik weet niet hoe ik nu x en y kan vinden.
[ Bericht 14% gewijzigd door Anoonumos op 08-10-2011 15:57:47 ]
Calculus van James Stewart
Section 7.1
Example 6
Ik probeer al een half uur lang te begijpen hoe men aan het antwoor na de zin: cos^2x = 1-sin^2x
Waarom staan er plots 2 integralen met daarvoor (n-1)
Section 7.1
Example 6
Ik probeer al een half uur lang te begijpen hoe men aan het antwoor na de zin: cos^2x = 1-sin^2x
Waarom staan er plots 2 integralen met daarvoor (n-1)
Impliciet differentiëren van de vergelijking van de curve naar x en subsitutie van y' = 3 levert als voorwaarde voor de coördinaten van de gevraagde punten op de curve:quote:
De kromme K bestaat uit alle punten
Deze kromme heeft een raaklijn L in het punt (0, 0).
(a) Geef de vergelijking van L in de vorm y = rx + b.
(b) Er zijn twee punten op K waar de raaklijnen zo zijn dat ze de lijn L
ergens loodrecht snijden. Bereken de co¨ordinaten van deze punten.
Met impliciet differentieren krijg ik bij a) L = -1/3 x.
Dus voor de andere raaklijn geldt helling = 3. Ik weet niet hoe ik nu x en y kan vinden.
(x + y)2 = (3/4)∙81
Nu jij weer.
[ Bericht 0% gewijzigd door Riparius op 08-10-2011 18:21:13 ]
Heeft iemand hier dat trapje waar staat hoeveel x je moet gaan van centiliter naar ml naar liter enz en meters naar centimeters naar decimeters enz.. ?
Dank
Dank
graag op anoniem
http://en.wikipedia.org/wiki/SI_prefix#List_of_SI_prefixesquote:
Heeft iemand hier dat trapje waar staat hoeveel x je moet gaan van centiliter naar ml naar liter enz en meters naar centimeters naar decimeters enz.. ?
Dank
Ja. Je bedoelt vast:quote:Op zaterdag 8 oktober 2011 16:58 schreef Sokz het volgende:
Domein van sq.(x-3)(x-5) is toch (x-3)(x-5) > 0?
dus:
(-∞,3) (5,+∞)?
3 en 5 ook.quote:
Domein van sq.(x-3)(x-5) is toch (x-3)(x-5) > 0?
dus:
(-∞,3) (5,+∞)?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Misschien heb je iets aan het blaadje dat voor me ligt, en dan vooral de zin na het woordje 'de'?quote:
Calculus van James Stewart
Section 7.1
Example 6
Ik probeer al een half uur lang te begijpen hoe men aan het antwoor na de zin: cos^2x = 1-sin^2x
Waarom staan er plots 2 integralen met daarvoor (n-1)
Lekker duidelijk zo. Jij denkt zeker dat iedereen hier die je mogelijk kan helpen een exemplaar van dat boek (en dan ook nog de juiste druk, die je niet vermeldt) bij de hand heeft?quote:
Calculus van James Stewart
Section 7.1
Example 6
Ik probeer al een half uur lang te begrijpen hoe men aan het antwoord komt na de zin: cos2x = 1-sin2x
Waarom staan er plots 2 integralen met daarvoor (n-1)
Ik heb hier een PDF, dus je boft. Het gaat om het afleiden van een recursieve formule voor de onbepaalde integraal van sinnx. De stap waar je over struikelt is gewoon elementaire algebra:
(n-1)∙sinn-2x∙cos2x = (n-1)∙sinn-2x∙(1 - sin2x) = (n-1)∙sinn-2x - (n-1)∙sinnx
Kijk anders even hier.
[ Bericht 4% gewijzigd door Riparius op 08-10-2011 18:18:38 ]
quote:
Yes bedankt beiden had ik 't toch wel correct. Kloteboek brengt me elke keer weer in de war met foute antwoorden. :Squote:
We must have (x - 3)(x - 5) > 0 i.e. 3 < x < 5 (using a sign diagram)
say what?quote:
[..]
We must have (x - 3)(x - 5) > 0 i.e. 3 < x < 5 (using a sign diagram)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Op
[tex]9x+27y - \frac{10}{81} * (x + y)^{3} = 0[/tex] implicitiet diffquote:
[..]
Impliciet differentiëren van de vergelijking van de curve naar x en subsitutie van y' = 3 levert als voorwaarde voor de coördinaten van de gevraagde punten op de curve:
(x + y)2 = 81
Nu jij weer.
[tex]9 + 27y' - \frac{30}{81} * (x+y)^{2} * (y + x*y')[/tex] y' = 3 substitueren
[tex]90 - \frac{30}{81} * (x+y)^{2} * (y + 3x)[/tex]
[tex](x+y)^{2} * (y + 3x) = 243[/tex]
Toch? Hoezo moet (x + y)2 dan 81 zijn?
Oeps!
[ Bericht 26% gewijzigd door Anoonumos op 08-10-2011 17:31:23 ]
Wat is trouwens e? Ik snap dat het een waarde heeft (2.7 ofzo) maar hoe komen ze aan dat getal?
Kijk pi is ook maar een raar tekentje maar dat is wel de verhouding tussen omtrek en diameter. Waar haalt men die e vandaan?
Kijk pi is ook maar een raar tekentje maar dat is wel de verhouding tussen omtrek en diameter. Waar haalt men die e vandaan?
y(x)=ex^2, toon aan dat y'(x) =/ y''(x) voor alle x.
Is dat gewoon een kwestie van de eerste en tweede orde afgeleide aan elkaar gelijkstellen en dan de discriminant berekenen? Ik heb hier geen antwoorden bij de hand.
Is dat gewoon een kwestie van de eerste en tweede orde afgeleide aan elkaar gelijkstellen en dan de discriminant berekenen? Ik heb hier geen antwoorden bij de hand.
Heb ik ook. Ben er wel mee bezig, maar heb eigenlijk geen idee waar het voor dient.quote:
Wat is trouwens e? Ik snap dat het een waarde heeft (2.7 ofzo) maar hoe komen ze aan dat getal?
Kijk pi is ook maar een raar tekentje maar dat is wel de verhouding tussen omtrek en diameter. Waar haalt men die e vandaan?
Oeps, stomme fout. Maar is het dan niet (x+y)˛ * 4 = 243, dus (x+y)˛ = 60.75?quote:
Alhoewel 81 mooier uitkomt.. maar afgeleide van (x+y)ł is hier toch 3(x+y)˛(1 + y')
[ Bericht 8% gewijzigd door Anoonumos op 08-10-2011 17:56:58 ]
Ja.quote:
y(x)=ex^2, toon aan dat y'(x) =/ y''(x) voor alle x.
Is dat gewoon een kwestie van de eerste en tweede orde afgeleide aan elkaar gelijkstellen en dan de discriminant berekenen? Ik heb hier geen antwoorden bij de hand.
quote:
De waarde van a waarvoor de afgeleide van a^x gelijk is aan a^x.
kijk PI werd me na het zien van http://upload.wikimedia.o(...)-Pi-unrolled-720.gif gelijk duidelijk. Is zoiets ook voor e?
| 1 2 3 4 5 6 7 8 9 10 11 | n: (1+1/n)^n: 1 2.00000000000000 21 2.65626321392610 41 2.68585634753775 61 2.69633049628226 81 2.70168999138345 101 2.70494597748516 121 2.70713368818803 141 2.70870477667918 161 2.70988774063937 181 2.71081059248709 |
Modelijke interpretatie: rentebetalingen. Als je op een kapitaal 1 aan het einde van het jaar een rente van 100% krijgt, dan heb je 1+1=2. Stel nu dat je ipv eenmaal per jaar, tweemaal per jaar (halverwege en aan het eind) een rente van 50% krijgt. Dan heb je halverwege het jaar 1+1/2, en aan het einde van het jaar heb je (1+1/2)*(1+1/2)=(1+1/2)^2. In het algemeen, als je het jaar in n stukjes verdeelt en aan het einde van elke periode een rente van 100/n % krijgt, dan heb je aan het einde van het jaar (1+1/n)^n. Als je nu n groter en groter maakt, komt het bedrag dat je aan het einde van het jaar hebt steeds dichter bij het getal e.
[ Bericht 23% gewijzigd door keesjeislief op 08-10-2011 18:04:44 ]
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Het oppervlak onder de functie y=1/x tussen x=1 en x=e is gelijk aan 1.
The biggest argument against democracy is a five minute discussion with the average voter.
Inderdaad, je hebt gelijk. Maar los de opgave nu eens verder op.quote:
[..]
IOeps, stomme fout. Maar is het dan niet (x+y)˛ * 4 = 243, dus (x+y)˛ = 60.75?
Alhoewel 81 mooier uitkomt.. maar afgeleide van (x+y)ł is hier toch 3(x+y)˛(1 + y')
quote:
[..]
Inderdaad, je hebt gelijk. Maar los de opgave nu eens verder op.
Dus
Delen door 9, x + 3y = ...
Dus je hebt 2 vergelijking en 2 onbekenden en dat kan ik op zich wel uitwerken, maar volgens mij komt hier geen mooi getal uit en dat vind ik toch vreemd.
Ja, z(3,2)=3.quote:
z(x, y) = min{x, 2y}
z(3, 2) = 2 (volgens de uitwerkingen)
Is het niet z(3, 2) = 3?
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Niet met decimale breuken werken. En vergeet niet dat er twee punten zijn op de curve die aan het gevraagde voldoen.quote:
[..]
Dus
Delen door 9, x + 3y = ...
Dus je hebt 2 vergelijking en 2 onbekenden en dat kan ik op zich wel uitwerken, maar volgens mij komt hier geen mooi getal uit en dat vind ik toch vreemd.
Was ik niet vergeten(wel in mijn post). Ik krijg nuquote:
[..]
Niet met decimale breuken werken. En vergeet niet dat er twee punten zijn op de curve die aan het gevraagde voldoen.
quote:Op zaterdag 8 oktober 2011 17:58 schreef keesjeislief het volgende:
maakt, komt het bedrag dat je aan het einde van het jaar hebt steeds dichter bij het getal e.
Dank beiden!quote:
[ afbeelding ]
Het oppervlak onder de functie y=1/x tussen x=1 en x=e is gelijk aan 1.
Dat klopt.quote:
[..]
Was ik niet vergeten(wel in mijn post). Ik krijg nuen dan nog de negatieve waarden hiervan voor de andere oplossing.
waarom staan twee lijnen loodrecht op elkaar als het product van de twee hellingen gelijk is aan -1?
Haha sorry, maar ik dacht dat de meesten hier wel met een bčtastudie Calculus hebben gekregen en dus al het boek in hun la hadden liggen, het betreft trouwens het vijfde drukquote:
[..]
Lekker duidelijk zo. Jij denkt zeker dat iedereen hier die je mogelijk kan helpen een exemplaar van dat boek (en dan ook nog de juiste druk, die je niet vermeldt) bij de hand heeft?
Ik heb hier een PDF, dus je boft. Het gaat om het afleiden van een recursieve formule voor de onbepaalde integraal van sinnx. De stap waar je over struikelt is gewoon elementaire algebra:
(n-1)∙sinn-2x∙cos2x = (n-1)∙sinn-2x∙(1 - sin2x) = (n-1)∙sinn-2x - (n-1)∙sinnx
Kijk anders even hier.
Trouwens de uitleg in je link begrijp ik nog minder dan het antwoord zelf, waar ik ook al een
voor heb...Wat ik niet begrijp is hoe je aan de laatste antwoord komt, (n-1)∙sinn-2x∙(1 - sin2x)
oke tot hier begrijp ik, maar:
= (n-1)∙sinn-2x - (n-1)∙sinnx
Ik weet dat het eerste deel vermenigvuldigd wordt met de 1 in het haakje, die wordt dus (n-1)∙sinn-2x, maar hoe ontstaat het tweede deel, daar kom ik maar niet uit
