[Bèta wiskunde] Huiswerk- en vragentopic

wat een naar ding...





dus het antwoord is de oplossing van de dv d/dp y(p) = -1/(1-p) y(p).

Beetje creatief knutselen met de geometrische rij, wat gebeurt er als je de identiteit 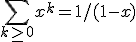differentieert naar x?

quote:

Op zaterdag 24 september 2011 16:55 schreef GlowMouse het volgende:


wat een naar ding...





dus het antwoord is de oplossing van de dv d/dp y(p) = -1/(1-p) y(p).

Dit klopt toch niet? Je vergeet een factor (k-2) bij het differentiëren naar p van de termen van de reeks en tevens is k(^k₂) = (k³ - k²)/2.

[ Bericht 1% gewijzigd door Riparius op 24-09-2011 19:36:07 ]

Glowmouse, ik zie niet waar je die [k^3-k] / 2 vandaan haalt.

quote:

Op zaterdag 24 september 2011 19:13 schreef thenxero het volgende:
Glowmouse, ik zie niet waar je die [k^3-k] / 2 vandaan haalt.

Ik denk dat je beter die geometrische som kunt gebruiken, dat zal ook wel de bedoeling van de opgave zijn denk ik.

quote:

Op zaterdag 24 september 2011 19:15 schreef keesjeislief het volgende:

[..]

Ik denk dat je beter die geometrische som kunt gebruiken, dat zal ook wel de bedoeling van de opgave zijn denk ik.

Als je die differentiëert krijg je trouwens



Maar ik weet niet echt wat ik met dat binomiaalcoëfficiënt aanmoet...

quote:

Op zaterdag 24 september 2011 19:13 schreef thenxero het volgende:
Glowmouse, ik zie niet waar je die [k^3-k] / 2 vandaan haalt.

(^k₂) = k(k-1)/2, dus k(^k₂) = (k³ - k²)/2. Maar de oplossing van Glowmouse klopt niet, ook al niet omdat hij een factor (k-2) vergeet.

quote:

Op zaterdag 24 september 2011 19:17 schreef thenxero het volgende:

[..]

Als je die differentiëert krijg je trouwens

Met de k in de som bedoel je? Als je nu gebruikt dat , dan kun je jouw som in delen schrijven die allemaal uit te drukken zijn als de eerste/tweede/... afgeleide van en kun je op die manier een uitdrukking voor jouw som vinden.

quote:

Op zaterdag 24 september 2011 19:21 schreef keesjeislief het volgende:

[..]

Met de k in de som bedoel je? Als je nu gebruikt dat , dan kun je jouw som in delen schrijven die allemaal uit te drukken zijn als de eerste/tweede/... afgeleide van en kun je op die manier een uitdrukking voor jouw som vinden.

Pff dat is nog een heel karwei. Je krijgt dan uiteindelijk een DV die je moet oplossen? Met de afgeleide van de rechterkant van die identiteit is vast makkelijker.

Zo'n gedoe voor een vraag uit de kansrekening, dat had ik niet verwacht .

quote:

Op zaterdag 24 september 2011 19:44 schreef thenxero het volgende:

[..]

Pff dat is nog een heel karwei.

Vind je? Lees eens wat werk van Leonard Euler, dat was een absolute virtuoos op het gebied van het manipuleren van oneindige reeksen en dan zie je pas echt dingen waar je perplex van staat.

quote:

Zo'n gedoe voor een vraag uit de kansrekening, dat had ik niet verwacht .

Is toch een mooie uitdaging?

Bekijk het eens als volgt (met dank aan keesjeislief). Beschouw een reeks waarvan de termen van de gedaante

(1) (1 - p)^k+1

zijn, en waarbij je k laat lopen van 2 tot ∞. Merk trouwens op dat deze reeks alleen convergent is voor |1 - p| < 1. Deze meetkundige reeks kun je gemakkelijk sommeren en daarmee uitdrukken in p. Neem nu van beide zijden van je identiteit de afgeleide naar p, dan zijn de termen van de nieuwe reeks te schrijven als:

(2) -k(1 - p)^k - (1 - p)^k

De som van de deeltermen van de gedaante (1 - p)^k kun je gemakkelijk uitdrukken in p, dit is namelijk gelijk aan de som van de termen van de gedaante (1) gedeeld door (1 - p). Met deze gegevens kun je ook de som van deeltermen van (2) van de gedaante k(1 - p)^k uitdrukken in p. Nu weer van (2) de afgeleide naar p nemen, dus de tweede afgeleide naar p van (1), en we krijgen

(3) k²(1 - p)^k-1 + k(1 - p)^k-1

We hebben al een uitdrukking in p voor de som van de termen van (3), namelijk de afgeleide naar p van de som van de termen van de gedaante (2), en aangezien de som van de deeltermen van (3) van de gedaante k(1 - p)^k-1 gelijk is aan de eerder bepaalde som van de termen van de gedaante k(1 - p)^k gedeeld door (1 - p) kunnen we met deze gegevens weer een uitdrukking in p voor de som van de deeltermen van (3) van de gedaante k²(1 - p)^k-1 afleiden. Nu weer (3) differentiëren naar p en we krijgen een uitdrukking die we kunnen schrijven als:

(4) -k²(k - 1)(1 - p)^k-2 - k²(1 - p)^k-2 + k(1 - p)^k-2

De som van de termen van de gedaante (4) uitgedrukt in p is bekend, want dit is de derde afgeleide van (1), en de som van de deeltermen van (4) van de gedaante k²(1 - p)^k-2 en k(1 - p)^k-2 kunnen we weer uitdrukken in p door de eerder gevonden uitdrukkingen in p voor de sommen van termen van de gedaantes k²(1 - p)^k-1 resp. k(1 - p)^k-1 te delen door (1 - p). En daarmee zijn we dan in staat om de som van de deeltermen van (4) van de gedaante k²(k - 1)(1 - p)^k-2 uit te drukken in p. De gevraagde som van de reeks bestaande uit termen van de gedaante k(^k₂)(1 - p)^k-2 is uiteraard de helft daarvan.

[ Bericht 0% gewijzigd door Riparius op 24-09-2011 21:30:39 ]

quote:

Op zaterdag 24 september 2011 19:09 schreef Riparius het volgende:

[..]

Dit klopt toch niet? Je vergeet een factor (k-2) bij het differentiëren naar p van de termen van de reeks en tevens is k(^k₂) = (k³ - k²)/2.

je hebt gelijk

Bewering: U1 en U2 deelruimtes van vectorruimte V, dan
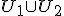is ook een deelruimte van V desda 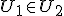of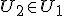

Aantonen dat de vereniging een deelruimte is als die voorwaarde geldt lukt me. Andersom niet.

Voor alle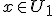 en alle 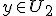geldt dat de som van x en y in de vereniging van U1 en U2 zit. Hoe kan ik daaruit concluderen dat 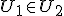of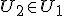
? Ik heb geprobeerd aan te nemen dat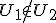 of 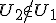en dan tegenspraak proberen te vinden, maar daar kom ik niet uit.

quote:

Op zondag 25 september 2011 14:18 schreef Anoonumos het volgende:
Bewering: U1 en U2 deelruimtes van vectorruimte V, dan
is ook een deelruimte van V desda of

Aantonen dat de vereniging een deelruimte is als die voorwaarde geldt lukt me. Andersom niet.

Voor alle en alle geldt dat de som van x en y in de vereniging van U1 en U2 zit. Hoe kan ik daaruit concluderen dat of
? Ik heb geprobeerd aan te nemen dat of en dan tegenspraak proberen te vinden, maar daar kom ik niet uit.

Latex tip: \subset

Als het niet geldt, dan is er een x in U₁-U₂ en een y in U₂-U₁. Nu jij weer.

Dat betekent meteen dat x + y niet in de vereniging van U1 en U2 zit, dus tegenspraak?
(edit)Nee dat klopt niet

Dus x + y >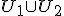

[ Bericht 27% gewijzigd door Anoonumos op 25-09-2011 14:38:37 ]

Wat bedoel je met ">" ?

Sorry, dat x + y buiten die doorsnede valt. Maar ik twijfel of je dat zo kan concluderen.

Wat betekent het dat iets in de vereniging van twee verzamelingen zit?

Het zit in de een, of in de ander (of beide).
Dus x + y zit niet in U1, niet in U2, dus ook niet in U1verenigdU2.

En waarom zit x+y niet in U1?

Deelruimte: u en v in deelruimte, u + v ook in deelruimte.
Andersom als x + y in een deelruimte zitten, dan x en y ook. Of mag je dat niet zomaar omdraaien?

Nee, pak bv. R₊, met x=5 en y=-1. dan zitten x en x+y er wel in, maar y niet. Hier kun je aantonen dat je op een tegenspraak uitkomt als x+y in U1 zit, maar dat moet je dan wel doen.

quote:

Op zaterdag 24 september 2011 16:22 schreef thenxero het volgende:
Hoe bereken ik dat

?

Binom staat voor het binomiaalcoëfficiënt.

Het is geen meetkundige rij ... maar het staat als rekenopgave in mijn textboek, dus zou toch met pen en papier moeten kunnen.

Graag wil ik nog even terugkomen op deze opgave omdat het toch met aanzienlijk minder rekenwerk blijkt te kunnen dan ik gisteren had aangegeven. Laten we de factor ½ van alle termen van de reeks even buiten beschouwing, dan gaat het om het sommeren van een reeks waarvan de termen van de volgende gedaante zijn:

(1) k²(k -1)(1 - p)^k-2

Als het nu ging om het sommeren van een reeks met termen van de gedaante k(k -1)(1 - p)^k-2, dan was het eenvoudig, aangezien de termen dan zijn op te vatten als de tweede afgeleide van termen van de gedaante (1 - p)^k, die een meetkundige reeks vormen. Maar in (1) hebben de termen een extra factor k.

Nemen we daarentegen de derde afgeleide van een meetkundige reeks met termen met een exponent k+1, dan krijgen we in de afgeleide reeks bij elke term een factor (k+1)k(k-1), en dus ook niet de gewenste factor k²(k-1). Maar nu kunnen we opmerken dat:

(2) k²(k-1) = (k+1-1)k(k-1) = (k+1)k(k-1) - k(k-1)

En dus hebben we ook:

(3) k²(k-1)(1 - p)^k-2 = (k+1)k(k-1)(1 - p)^k-2 - k(k-1)(1 - p)^k-2

Dit betekent niets anders dan dat je de reeks met termen van de gedaante (1) kunt opvatten als het verschil van twee reeksen waarvan de eerste de derde afgeleide is van een geometrische reeks met termen van de gedaante -(1 - p)^k+1 terwijl de tweede reeks de tweede afgeleide is van een geometrische reeks met termen van de gedaante (1 - p)^k. Dus:

(4) Σ_k=2^∞ k²(k-1)(1 - p)^k-2 = Σ_k=2^∞ (k+1)k(k-1)(1 - p)^k-2 - Σ_k=2^∞ k(k-1)(1 - p)^k-2 (|1 - p| <1)

De som van elk van beide reeksen in het rechterlid van (4) is eenvoudig te bepalen. Nemen we eerst de geometrische reeks met termen van de gedaante -(1 - p)^k+1, k = 2..∞. De eerste term hiervan is -(1 - p)³ en de reden (1 - p), dus:

(5) Σ_k=2^∞ -(1 - p)^k+1 = -(1 - p)³/p = p² - 3p + 3 - p^-1 (|1 - p| < 1)

Beide leden driemaal differentiëren naar p levert dan:

(6) Σ_k=2^∞ (k+1)k(k-1)(1 - p)^k-2 = 6p^-4 (|1 - p| < 1)

Nu de geometrische reeks met termen van de gedaante (1 - p)^k, k = 2..∞. De eerste term hiervan is (1 - p)² en de reden (1 - p), dus:

(7) Σ_k=2^∞ (1 - p)^k = (1 - p)²/p = p - 2 + p^-1 (|1 - p| < 1)

Beide leden tweemaal differentiëren naar p geeft:

(8) Σ_k=2^∞ k(k-1)(1 - p)^k-2 = 2p^-3 (|1 - p| < 1)

Uit (4), (6) en (8) volgt nu:

(9) Σ_k=2^∞ k²(k-1)(1 - p)^k-2 = 6p^-4 - 2p^-3 = (6 - 2p)/p⁴ (|1 - p| < 1)

Beide leden vermenigvuldigen met ½ en terugsubstitueren van ½k(k - 1) = (^k₂) levert dan:

(10) Σ_k=2^∞ k(^k₂)(1 - p)^k-2 = (3 - p)/p⁴ (|1 - p| < 1)

QED

[ Bericht 0% gewijzigd door Riparius op 26-09-2011 03:02:11 ]

quote:

Op zondag 25 september 2011 16:07 schreef GlowMouse het volgende:
Nee, pak bv. R₊, met x=5 en y=-1. dan zitten x en x+y er wel in, maar y niet. Hier kun je aantonen dat je op een tegenspraak uitkomt als x+y in U1 zit, maar dat moet je dan wel doen.

De tegenspraak zou kunnen zijn dat U1 toch een deelverzameling is van U2 of andersom, of dat y toch in U1 zit of x toch in U2. Maar ik zie niet hoe dit volgt als x + y in U1 zit. Ik begrijp dat ik lastig ben, maar ik waardeer jullie hulp.

x zit in U₁-U₂ en y in U₂-U₁.

Stel x+y zit in U₁, kun je dan aantonen dat y ook in U₁ zit, om zo op een tegenspraak te komen? Je weet dat x in U₁ zit, dus -x ook.

Aha. Dus (x+y) + -x = y ook want het is een deelruimte. Ik hoop dat het me binnenkort zelf lukt om zoiets te bedenken. Bedankt.

Brengen de vectoren (1,0,-1), (2,1,1) en (1,0,1) R³ voort?
Ja, voor elke x.y,z in R³ geldt dat het een lineaire combinatie is van deze 3 vectoren. (neem scalars c1 = 1/2 (x - y - z), c2 = y , c3 = 1/2 (x - 3y + z)

Brengen de vectoren (1,2,3), (4,5,6) en (7,8,9) R³ voort?
Nee, c1 c2 en c3 blijf ik afhankelijk van elkaar houden. Dus er is geen lineaire combinatie mogelijk.

Doe ik dit goed? In het dictaat staat het amper uitgelegd, dus ik moet me redden met filmpjes van Khan Academy.

quote:

Op zondag 25 september 2011 18:30 schreef Anoonumos het volgende:
Brengen de vectoren (1,2,3), (4,5,6) en (7,8,9) R³ voort?
Nee, c1 c2 en c3 blijf ik afhankelijk van elkaar houden. Dus er is geen lineaire combinatie mogelijk.

Waarom volgt daaruit dat ze R³ niet voortbrengen?

Als een element in R³ niet geschreven kan worden als een lineaire combinatie van 3 bepaalde vectoren, dan brengen die 3 vectoren R³ niet voort.

En waarom is er een element dat geen lineaire combinatie is?

Leuk die oneliners van thabit die in één keer de vinger op de zere plek legt.

OT:Heeft iemand een leuke denk opgave over analystische meetkunde; rechte lijnen en cirkels?