SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Ik heb een vraag over projectieve meetkunde. In het specifiek over de cross ratio. De cross ratio is invariant onder projectieve transformaties.Het is niet de enige invariant, want bv (cros ratio)^2 is ook invariant onder projectieve transformaties. Hoe bewijs ik de volgende stelling: Elke invariant van 4 punten is een functie van de cross ratio.
Ik gebruik de volgende definitie; cross ratio: [p,q;r,s]=(r-p)*(s-q)/(r-q)*(s-p). Alle hulp is welkom.
Ik gebruik de volgende definitie; cross ratio: [p,q;r,s]=(r-p)*(s-q)/(r-q)*(s-p). Alle hulp is welkom.
-


Het Nederlandse woord voor "cross ratio" is "dubbelverhouding". Je zou het volgende kunnen bewijzen. Gegeven twee viertallen punten met dezelfde dubbelverhouding, bestaat er een projectieve transformatie die het ene viertal in het andere overvoert.quote:Op vrijdag 29 juli 2011 21:17 schreef gaussie het volgende:
Ik heb een vraag over projectieve meetkunde. In het specifiek over de cross ratio. De cross ratio is invariant onder projectieve transformaties.Het is niet de enige invariant, want bv (cros ratio)^2 is ook invariant onder projectieve transformaties. Hoe bewijs ik de volgende stelling: Elke invariant van 4 punten is een functie van de cross ratio.
Ik gebruik de volgende definitie; cross ratio: [p,q;r,s]=(r-p)*(s-q)/(r-q)*(s-p). Alle hulp is welkom.


Vanaf nu kun je met de [tex]-tag Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hey hey,
Ik ben op zoek naar handige constructies/voorbeelden (met de hand en/of met Magma) van krommen en morfismen met de volgende eigenschappen:
 is een kromme over
is een kromme over 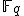 van geslacht
van geslacht 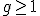 en er is een morfisme
en er is een morfisme 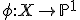 van graad
van graad 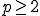 met de eigenschap
met de eigenschap 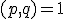 en
en 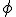 is Galois over
is Galois over 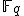 : Er is een automorfisme
: Er is een automorfisme 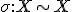 van orde
van orde  gedefinieerd over
gedefinieerd over 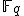 met
met 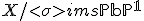 .
.
Alvast heeeeeeeeeeeeeeeeeeeeeeeeel veeeeel dank.
[ Bericht 0% gewijzigd door morfine2011 op 30-07-2011 13:30:10 ]
Ik ben op zoek naar handige constructies/voorbeelden (met de hand en/of met Magma) van krommen en morfismen met de volgende eigenschappen:
Alvast heeeeeeeeeeeeeeeeeeeeeeeeel veeeeel dank.
[ Bericht 0% gewijzigd door morfine2011 op 30-07-2011 13:30:10 ]


Kudo!!!quote:Op vrijdag 29 juli 2011 21:48 schreef GlowMouse het volgende:
Vanaf nu kun je met de [tex]-tag Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).


wat ben ik blij dat ik mijn algebra-vakken al ooit heb gehaald.. Sterkte ermee.quote:Op zaterdag 30 juli 2011 13:24 schreef morfine2011 het volgende:
Hey hey,
Ik ben op zoek naar handige constructies/voorbeelden (met de hand en/of met Magma) van krommen en morfismen met de volgende eigenschappen:is een kromme over
van geslacht
en er is een morfisme
van graad
met de eigenschap
en
is Galois over
: Er is een automorfisme
van orde
gedefinieerd over
met
.
Alvast heeeeeeeeeeeeeeeeeeeeeeeeel veeeeel dank.


quote:Op maandag 1 augustus 2011 14:59 schreef Don_Vanelli het volgende:
[..]
wat ben ik blij dat ik mijn algebra-vakken al ooit heb gehaald.. Sterkte ermee.


Ik denk dat het handiger is om de vraag iets preciezer te stellen; wat wil je nu eigenlijk weten?quote:Op zaterdag 30 juli 2011 13:24 schreef morfine2011 het volgende:
Hey hey,
Ik ben op zoek naar handige constructies/voorbeelden (met de hand en/of met Magma) van krommen en morfismen met de volgende eigenschappen:is een kromme over
van geslacht
en er is een morfisme
van graad
met de eigenschap
en
is Galois over
: Er is een automorfisme
van orde
gedefinieerd over
met
.
Alvast heeeeeeeeeeeeeeeeeeeeeeeeel veeeeel dank.
Het moet denk ik wel mogelijk zijn om met klassenlichamentheorie aan de slag te gaan en op die manier cyclische uitbreidingen van Fq(t) te construeren (wel oppassen dat je het constantenlichaam gelijk aan Fq houdt). Wegens de voorwaarde (p,q)=1 zal alles ook nog eens tam vertakt zijn. Als je enkel veel voorbeelden wenst te vinden, kun je je concentreren op gevallen waarin weinig (bijvoorbeeld 3) punten vertakt zijn.
Er zal vast ook wel wat literatuur te vinden zijn over dit probleem, wat in feite neerkomt op een generalisatie van Kronecker-Weber naar het geval van functielichamen.


Wat ik eigenlijk deed en wil doen kan ik het best illustreren met een voorbeeld:
Eerst maak ik een kromme:
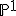
de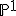 .
.
 bepaal ik de bijbehorende vezel.
bepaal ik de bijbehorende vezel.
 een
een 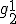 linear systeem die door
linear systeem die door 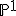 geparametriseerd wordt. Zo geldt:
geparametriseerd wordt. Zo geldt:
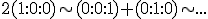
(ik hoef niet perse te eisen dat (p,q)=1).
Merk op dat de pullbacks van de rationale punten rationale punten zijn...
Wat ik boven gedaan heb, wil ik doen voor krommen met bijv. een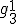 linear systeem die over
linear systeem die over 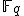 gedefinieerd is. Een manier om dus zulke lineaire systemen te vinden is een morfisme te maken naar
gedefinieerd is. Een manier om dus zulke lineaire systemen te vinden is een morfisme te maken naar 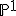 en dan kijken naar de pullbacks van rationale punten op
en dan kijken naar de pullbacks van rationale punten op 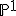 .
.
Een idee is te kijken naar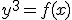 over
over 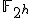 Het lukt me niet om alleen rationale pullbacks te krijgen..... en daar zit ik dus vast mee.
Het lukt me niet om alleen rationale pullbacks te krijgen..... en daar zit ik dus vast mee.
Eerst maak ik een kromme:
en dan eenquote:F<w>:=GF(2^2);
K<x,y,z>:=PolynomialRing(F,3);
f:=x^2*y+w*y^2*z+w^2*z^2*x;
X:=Curve(ProjectiveSpace(F,2),f);
Daarna bepaal ik de plaatsen en definieer ik een morfisme van mijn kromme naarquote:Y:=Curve(ProjectiveSpace(F,1));
de
Nu komt het: voor ieder punt uitquote:plcsY:=Places(Y,1);
phi:=map<X->Y|[x,y]>;
phi;
De uitvoer behorende bij de laatste quote is:quote:L:=[];
for i:=1 to #plcsY do L[i]:= Decomposition(Pullback(phi,plcsY[i])); end for;
L;
In feite er is opquote:[
[
<Place at (1 : 0 : 0), 2>
],
[
<Place at (0 : 0 : 1), 1>,
<Place at (0 : 1 : 0), 1>
],
[
<Place at (w : 1 : 1), 1>,
<Place at (w^2 : w : 1), 1>
],
[
<Place at (1 : w : 1), 1>,
<Place at (w : w^2 : 1), 1>
],
[
<Place at (1 : 1 : 1), 1>,
<Place at (w^2 : w^2 : 1), 1>
]
]
(ik hoef niet perse te eisen dat (p,q)=1).
Merk op dat de pullbacks van de rationale punten rationale punten zijn...
Wat ik boven gedaan heb, wil ik doen voor krommen met bijv. een
Een idee is te kijken naar


Ja omdat onder alle linear fractional transformations (dus van de vorm f(x)=ax+b/cx+d) de dubbelverhouding hetzelfde blijft. Dus met andere woorden [f(p),f(q),f(r),f(s)]=[p,q,r,s]. Hoe nu verder?quote:Op vrijdag 29 juli 2011 21:27 schreef thabit het volgende:
[..]
Het Nederlandse woord voor "cross ratio" is "dubbelverhouding". Je zou het volgende kunnen bewijzen. Gegeven twee viertallen punten met dezelfde dubbelverhouding, bestaat er een projectieve transformatie die het ene viertal in het andere overvoert.
-


Ook in het voorbeeld is het niet zo dat van alle rationale punten de inverse beelden uit rationale punten bestaan. Alleen degenen waarvan je al weet dat er een rationaal punt boven ligt. Aangezien de graad 2 is, blijft er weinig keus over voor het andere punt. Dus ik snap nog steeds niet helemaal wat je vraag nu precies is.quote:Op dinsdag 2 augustus 2011 19:53 schreef morfine2011 het volgende:
Wat ik eigenlijk deed en wil doen kan ik het best illustreren met een voorbeeld:
Eerst maak ik een kromme:
[..]
en dan een
[..]
Daarna bepaal ik de plaatsen en definieer ik een morfisme van mijn kromme naar
de.
[..]
Nu komt het: voor ieder punt uitbepaal ik de bijbehorende vezel.
[..]
De uitvoer behorende bij de laatste quote is:
[..]
In feite er is opeen
linear systeem die door
geparametriseerd wordt. Zo geldt:
(ik hoef niet perse te eisen dat (p,q)=1).
Merk op dat de pullbacks van de rationale punten rationale punten zijn...
Wat ik boven gedaan heb, wil ik doen voor krommen met bijv. eenlinear systeem die over
gedefinieerd is. Een manier om dus zulke lineaire systemen te vinden is een morfisme te maken naar
en dan kijken naar de pullbacks van rationale punten op
.
Een idee is te kijken naarover
Het lukt me niet om alleen rationale pullbacks te krijgen..... en daar zit ik dus vast mee.


Wel, je kan bijvoorbeeld gebruiken dat je elk drietal verschillende punten op 0, 1, en oneindig kan afbeelden dmv een gebroken lineaire transformatie.quote:Op dinsdag 2 augustus 2011 21:48 schreef gaussie het volgende:
[..]
Ja omdat onder alle linear fractional transformations (dus van de vorm f(x)=ax+b/cx+d) de dubbelverhouding hetzelfde blijft. Dus met andere woorden [f(p),f(q),f(r),f(s)]=[p,q,r,s]. Hoe nu verder?


Iets duidelijker: ik wil een kromme X en een afbeelding naar P^1 kunnen maken met de eigenschap dat als een rationaal punt op P^1 een rationaal punt heeft in de vezel dan zijn de overige punten in die vezel ook rationaal. Dus een generalisatie van het geval wat ik boven heb beschreven: i.p.v een morfisme van graad 2, wil ik het voor graad 3 of een hoger priem graad doen, hier is X van geslacht min 3.quote:. Alleen degenen waarvan je al weet dat er een rationaal punt boven ligt. Aangezien de graad 2 is, blijft er weinig keus over voor het andere punt.


Even wat gebrainstorm:
Stel K=Fq(X) en neem aan dat K/Fq(t) separabel is. Zij L de Galoisafsluiting van K over Fq(t) en laat G de Galoisgroep zijn, die we zien als permutatiegroep op de verzameling Hom(K, L) van lichaamsinbeddingen van K in L over Fq(t).
Als we een rationaal punt hebben, dan is dat een element waarop Frobq triviaal werkt. Frobq werkt ook op de vezel waarin dat punt ligt. Is deze vezel onvertakt, dan kunnen we Frobq liften naar een element g van G; het cykeltype dat g op de vezel heeft is hetzelfde als op Hom(K, L).
Het lijkt dus handig als de permutatiegroep G aan de volgende eigenschap voldoet: het triviale element is het enige element met een dekpunt. Als dat zo is, dan zal dus (behalve misschien in vertakte vezels) aan het probleem voldaan zijn; niet alleen over Fq, maar ook over elke uitbreiding daarvan.
Er zijn meer voorbeelden van zulke G dan alleen cyclische groepen. Als G bijvoorbeeld op zichzelf werkt middels een Cayley-actie, dan ben je er ook (kortom als K Galois is over Fq(t)).
Anderzijds is het gemiddeld aantal dekpunten van de elementen van een eindige permutatiegroep altijd gelijk aan het aantal banen, dus gelijk aan 1 in ons geval. Als K/Fq(t) niet Galois is, dan zal G groter zijn dan de verzameling waarop ze werkt en dus niet-triviale elementen met dekpunten bevatten. Kortom, de groep G zal aan de gewenste eigenschap voldoen desda K/Fq(t) Galois is.
Uiteraard kunnen er ook voorbeelden bestaan waarin G niet aan deze eigenschap voldoet; dan heb je gewoon simpelweg het resultaat niet voor elke willekeurige uitbreiding van Fq. De constructie van zulke voorbeelden zal wel wat ingewikkelder zijn.
Er is wel het een en ander geschreven over het zoeken naar polynomen met gegeven Galoisgroepen, in elk geval over lichamen zoals Q en Q(t), maar ook wel over andere lichamen. De resultaten over Q(t) zou je misschien kunnen hanteren en dan hopen dat er nog wat van de Galoisgroep overblijft als je de coëfficiënten naar Fq reduceert. Misschien is er in de volgende boeken wat te vinden:
Jensen, Ledet, Yui - Generic Polynomials: Constructive Aspects of the Inverse Galois Problem
Malle & Matzat - Inverse Galois Theory
Serre - Topics in Galois Theory
Stel K=Fq(X) en neem aan dat K/Fq(t) separabel is. Zij L de Galoisafsluiting van K over Fq(t) en laat G de Galoisgroep zijn, die we zien als permutatiegroep op de verzameling Hom(K, L) van lichaamsinbeddingen van K in L over Fq(t).
Als we een rationaal punt hebben, dan is dat een element waarop Frobq triviaal werkt. Frobq werkt ook op de vezel waarin dat punt ligt. Is deze vezel onvertakt, dan kunnen we Frobq liften naar een element g van G; het cykeltype dat g op de vezel heeft is hetzelfde als op Hom(K, L).
Het lijkt dus handig als de permutatiegroep G aan de volgende eigenschap voldoet: het triviale element is het enige element met een dekpunt. Als dat zo is, dan zal dus (behalve misschien in vertakte vezels) aan het probleem voldaan zijn; niet alleen over Fq, maar ook over elke uitbreiding daarvan.
Er zijn meer voorbeelden van zulke G dan alleen cyclische groepen. Als G bijvoorbeeld op zichzelf werkt middels een Cayley-actie, dan ben je er ook (kortom als K Galois is over Fq(t)).
Anderzijds is het gemiddeld aantal dekpunten van de elementen van een eindige permutatiegroep altijd gelijk aan het aantal banen, dus gelijk aan 1 in ons geval. Als K/Fq(t) niet Galois is, dan zal G groter zijn dan de verzameling waarop ze werkt en dus niet-triviale elementen met dekpunten bevatten. Kortom, de groep G zal aan de gewenste eigenschap voldoen desda K/Fq(t) Galois is.
Uiteraard kunnen er ook voorbeelden bestaan waarin G niet aan deze eigenschap voldoet; dan heb je gewoon simpelweg het resultaat niet voor elke willekeurige uitbreiding van Fq. De constructie van zulke voorbeelden zal wel wat ingewikkelder zijn.
Er is wel het een en ander geschreven over het zoeken naar polynomen met gegeven Galoisgroepen, in elk geval over lichamen zoals Q en Q(t), maar ook wel over andere lichamen. De resultaten over Q(t) zou je misschien kunnen hanteren en dan hopen dat er nog wat van de Galoisgroep overblijft als je de coëfficiënten naar Fq reduceert. Misschien is er in de volgende boeken wat te vinden:
Jensen, Ledet, Yui - Generic Polynomials: Constructive Aspects of the Inverse Galois Problem
Malle & Matzat - Inverse Galois Theory
Serre - Topics in Galois Theory


Bedankt voor de uitleg,quote:Op dinsdag 26 juli 2011 02:03 schreef Riparius het volgende:
[..]
Bekijk het eens als volgt. De cosinus en de sinus zijn periodieke functies met een periode 2π. Dat betekent dus dat:
(1) cos(3/2∙π + α) = cos (α - 1/2∙π)
Je weet ook dat de cosinusfunctie een even functie is, i.e. cos(-θ) = cos θ, en dus:
(2) cos (α - 1/2∙π) = cos (1/2∙π - α)
Nu is de cosinus van een hoek gelijk aan de sinus van het complement (daar komt ook de naam cosinus vandaan), dus:
(3) cos (1/2∙π - α) = sin α
Uit (1), (2) en (3) volgt uiteraard dat cos(3/2∙π + α) = sin α
Met een tekening is dit ook te zien aan de hand van de eenheidscirkel. Kies een punt op de eenheidscirkel boven de x-as, en noem de hoek van de radius naar dat punt met de positieve x-as α, dan is de sinus van die hoek positief, de sinus van α is immers per definitie de y-coördinaat van het beeldpunt van (1;0) bij een rotatie over een hoek α om de oorsprong. Doe je er nu 3/2∙π bij, dan kom je uit op een punt op de eenheidscirkel in de rechter helft van het vlak, aangezien 3/2∙π rad correspondeert met 3/4 van de omtrek van de eenheidscirkel. Ik denk dat je over het hoofd ziet dat de cosinus van een hoek (c.q. rotatie) per definitie de x-coördinaat is van het beeldpunt van (1;0) bij een rotatie om de oorsprong. En de x-coördinaat van een punt rechts van de y-as is positief. Ergo, als sin α positief is, dan moet cos(α + 3/2∙π) ook positief zijn, en omgekeerd. Je kunt dus ook zonder herleidingen meteen inzien dat cos(α + 3/2π) niet gelijk kan zijn aan -sin α.
Ik heb net na terugkomst van de vakantie de som opnieuw gedaan en het simpelweg uitgetekend mbv een eenheidscirkel, en now it all makes sense!.....stom dat ik het niet inzag.
Nogmaals bedankt!


Ik vroeg mij af hoe jullie al die kennis van wiskunde in het hoofd blijven houden. Tijdens het leren van nieuwe theorieën vergeet ik vaak de oude en blijven enkel de regels zitten. Hierdoor begrijp ik de nieuwe theorie vaak niet zo goed.
Ik ben nu bijvoorbeeld bezig met het uitrekenen van varianties met matricen. In deze theorie gebruiken ze getransponeerde matricen. Ik herinner mij dan nog wel dat
(A*B)^t (^t = transpose) gelijk staat aan (B^t)*(A^t), maar niet waarom dat ook alweer is. Ik heb het echter wel ooit gesnapt. Hierdoor verlies ik een hoop inzicht van de nieuwe theorie.
[ Bericht 2% gewijzigd door JohnSpek op 04-08-2011 19:55:43 ]
Ik ben nu bijvoorbeeld bezig met het uitrekenen van varianties met matricen. In deze theorie gebruiken ze getransponeerde matricen. Ik herinner mij dan nog wel dat
(A*B)^t (^t = transpose) gelijk staat aan (B^t)*(A^t), maar niet waarom dat ook alweer is. Ik heb het echter wel ooit gesnapt. Hierdoor verlies ik een hoop inzicht van de nieuwe theorie.
[ Bericht 2% gewijzigd door JohnSpek op 04-08-2011 19:55:43 ]


Veel bewijzen uit het eerste jaar kan ik nu zo opschrijven omdat ze helemaal niet zo lastig zijn. Af en toe kijk ik terug, en af en toe maakt het mij niet uit. Jouw transposevoorbeeld zou ik zo uitschrijven door te kijken waaraan element (i,j) gelijk is, maar die moeite zou ik niet nemen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je zou die transposeregel even snel kunnen checken met twee 2x2 matrices bijvoorbeeld, zodat je wat meer inzicht hebt hoe het in elkaar zit. Dat kan je dan algemeen gaan opschrijven maar dat is gewoon geen leuk klusje. 


Valt wel mee, één regeltje met 3 gelijkheidstekens.quote:Op donderdag 4 augustus 2011 21:09 schreef thenxero het volgende:
Dat kan je dan algemeen gaan opschrijven maar dat is gewoon geen leuk klusje.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Klopt maar het klooien met indices of matrixelementen vind/vond ik nooit leukquote:Op donderdag 4 augustus 2011 21:11 schreef GlowMouse het volgende:
[..]
Valt wel mee, één regeltje met 3 gelijkheidstekens.


Als je bang bent voor indices dan heb je het niet vaak genoeg gedaan.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ben niet bang maar vind het gewoon saai.quote:Op donderdag 4 augustus 2011 22:53 schreef GlowMouse het volgende:
Als je bang bent voor indices dan heb je het niet vaak genoeg gedaan.


Inderdaad, zolang je die dingen niet kan dromen ken je het nog nietquote:Op donderdag 4 augustus 2011 22:53 schreef GlowMouse het volgende:
Als je bang bent voor indices dan heb je het niet vaak genoeg gedaan.
Beneath the gold, bitter steel


Ik ben bezig met een opgave, maar ik zie even niet wat ze doen.
Het gaat om deze:
(1/5)q1-(4/5) q2(3/5)
(3/5)qq(1/5) q2-(2/5)
(een breuk dus)
Ze maken daar het volgende van:
q2
3q1
Maar ik zie niet hoe ze daar aan komen. Ok, ik begrijp dat je die eerste met 5 kunt vermenigvuldigen, maar ik kom dan op
q1-4q23
3q1q2-2
uit. Wat mis ik dat ze doen?
(sorry voor de onduidelijke manier van neerzetten, vond dit al moeilijk genoeg )
)
[ Bericht 0% gewijzigd door maen op 07-08-2011 11:31:44 ]
Het gaat om deze:
(1/5)q1-(4/5) q2(3/5)
(3/5)qq(1/5) q2-(2/5)
(een breuk dus)
Ze maken daar het volgende van:
q2
3q1
Maar ik zie niet hoe ze daar aan komen. Ok, ik begrijp dat je die eerste met 5 kunt vermenigvuldigen, maar ik kom dan op
q1-4q23
3q1q2-2
uit. Wat mis ik dat ze doen?
(sorry voor de onduidelijke manier van neerzetten, vond dit al moeilijk genoeg
[ Bericht 0% gewijzigd door maen op 07-08-2011 11:31:44 ]


Bedenk dat: x -y = 1 / (x y)quote:Op zondag 7 augustus 2011 11:23 schreef maen het volgende:
Ik ben bezig met een opgave, maar ik zie even niet wat ze doen.
Het gaat om deze:
(1/5)q1-(4/5) q2(3/5)
(3/5)qq(1/5) q2-(2/5)
(een breuk dus)
Ze maken daar het volgende van:
q2
3q1
Maar ik zie niet hoe ze daar aan komen. Ok, ik begrijp dat je die eerste met 5 kunt vermenigvuldigen, maar ik kom dan op
q1-4q23
3q1q2-2
uit. Wat mis ik dat ze doen?
(sorry voor de onduidelijke manier van neerzetten, vond dit al moeilijk genoeg)
En: x a . xb = x (a+b)
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]


Hmm bedankt, maar dan zie ik het nog niet..quote:Op zondag 7 augustus 2011 11:35 schreef Nelis89 het volgende:
[..]
Bedenk dat: x -y = 1 / (x y)
En: x a . xb = x (a+b)


Ik heb de volgende opdracht:
syntax = u'x = du/dx
"Find dz expressed in terms of dx and dy when u = u(x,y)."
z = (x^2)*u
Ik gebruik de definitie dz = (z'x) * (dx) + (z'u) * (du)
Dan ga ik invullen:
Aangezien u een functie is van x gebruik ik de ketting regel.
z'x = (z'x)* (x') + (z'u) * (u'x)
z'x = (2xu) * 1 + (x^2)* (u'x)
du = (dx) * (u'x) + (dy) * (u'y)
z'u = x^2
Dit invullen:
dz = ((2xu) * 1 + (x^2)* (u'x)) * (dx) + (x^2) * ((dx) * (u'x) + (dy) * (u'y))
dz = (2xu)*(dx) + (x^2)*(u'x)*(dx) + (x^2)*(dx)*(u'x) + (dy)*(x^2)*(u'y)
dz = (2xu)*(dx) + 2(x^2)*(u'x)*(dx) + (dy)*(x^2)*(u'y)
dz = (2xu)*(dx) + (x^2)*(2*(u'x)*(dx) + (dy)*(u'y))
Nu is het goede antwoord volgens het antwoordenboek bijna hetzelfde namelijk:
dz = (2xu)*(dx) + (x^2)*((u'x)*(dx) + (dy)*(u'y))
Ik doe dus iets fout, alleen geen idee waar.
Ook heb ik het gevoel dat ik nogal lang bezig ben met een relatief makkelijke formule.
Methode 2:
Ik heb net een andere methode geprobeerd door gebruik te maken van de differential regels.
z = (x^2)*(u)
dz = d((x^2)*(u))
Definitie:
d((f)*(g)) = d(f)*(g) + d(g)*(f)
= d(x^2)* (u) + d(u) * (x^2)
= (2xu)*(dx)*(x^2) * ( (dy)* (u'y) + (dx) * (u'x))
Dan komt hij wel uit, snap echter nog steeds niet waarom het via methode 1 niet werkt.
[ Bericht 60% gewijzigd door JohnSpek op 07-08-2011 12:10:47 ]
syntax = u'x = du/dx
"Find dz expressed in terms of dx and dy when u = u(x,y)."
z = (x^2)*u
Ik gebruik de definitie dz = (z'x) * (dx) + (z'u) * (du)
Dan ga ik invullen:
Aangezien u een functie is van x gebruik ik de ketting regel.
z'x = (z'x)* (x') + (z'u) * (u'x)
z'x = (2xu) * 1 + (x^2)* (u'x)
du = (dx) * (u'x) + (dy) * (u'y)
z'u = x^2
Dit invullen:
dz = ((2xu) * 1 + (x^2)* (u'x)) * (dx) + (x^2) * ((dx) * (u'x) + (dy) * (u'y))
dz = (2xu)*(dx) + (x^2)*(u'x)*(dx) + (x^2)*(dx)*(u'x) + (dy)*(x^2)*(u'y)
dz = (2xu)*(dx) + 2(x^2)*(u'x)*(dx) + (dy)*(x^2)*(u'y)
dz = (2xu)*(dx) + (x^2)*(2*(u'x)*(dx) + (dy)*(u'y))
Nu is het goede antwoord volgens het antwoordenboek bijna hetzelfde namelijk:
dz = (2xu)*(dx) + (x^2)*((u'x)*(dx) + (dy)*(u'y))
Ik doe dus iets fout, alleen geen idee waar.
Ook heb ik het gevoel dat ik nogal lang bezig ben met een relatief makkelijke formule.
Methode 2:
Ik heb net een andere methode geprobeerd door gebruik te maken van de differential regels.
z = (x^2)*(u)
dz = d((x^2)*(u))
Definitie:
d((f)*(g)) = d(f)*(g) + d(g)*(f)
= d(x^2)* (u) + d(u) * (x^2)
= (2xu)*(dx)*(x^2) * ( (dy)* (u'y) + (dx) * (u'x))
Dan komt hij wel uit, snap echter nog steeds niet waarom het via methode 1 niet werkt.
[ Bericht 60% gewijzigd door JohnSpek op 07-08-2011 12:10:47 ]


z'x = 2xuquote:Op zondag 7 augustus 2011 11:46 schreef JohnSpek het volgende:
Ik heb de volgende opdracht:
syntax = u'x = du/dx
"Find dz expressed in terms of dx and dy when u = u(x,y)."
z = (x^2)*u
Ik gebruik de definitie dz = (z'x) * (dx) + (z'u) * (du)
Dan ga ik invullen:
Aangezien u een functie is van x gebruik ik de ketting regel.
z'x = (z'x)* (x') + (z'u) * (u'x)
z'x = (2xu) * 1 + (x^2)* (u'x)
du = (dx) * (u'x) + (dy) * (u'y)
z'u = x^2
Dit invullen:
dz = ((2xu) * 1 + (x^2)* (u'x)) * (dx) + (x^2) * ((dx) * (u'x) + (dy) * (u'y))
dz = (2xu)*(dx) + (x^2)*(u'x)*(dx) + (x^2)*(dx)*(u'x) + (dy)*(x^2)*(u'y)
dz = (2xu)*(dx) + 2(x^2)*(u'x)*(dx) + (dy)*(x^2)*(u'y)
dz = (2xu)*(dx) + (x^2)*(2*(u'x)*(dx) + (dy)*(u'y))
Nu is het goede antwoord volgens het antwoordenboek bijna hetzelfde namelijk:
dz = (2xu)*(dx) + (x^2)*(*(u'x)*(dx) + (dy)*(u'y))
Ik doe dus iets fout, alleen geen idee waar.
Ook heb ik het gevoel dat ik nogal lang bezig ben met een relatief makkelijke formule.
z'u doe je wel goed
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]


Mmmh dan haal ik iets door de war.quote:
Zou je kunnen uitleggen waarom z'x = 2xu
(u) hangt toch af van (x), waarom beschouw je (u) hier als constante?


dz/dx = 2 x u + x² du/dx
Ik vind je notaties een beetje vaag dus dat is lastig te lezen zo. De kettingregel is trouwens geen definitie, maar kan je gewoon bewijzen vanuit de definitie van de afgeleide. Ik vind de opgave sowieso vreemd dat je infinitesimalen moet uitdrukken in andere infinitesimalen...
Ik vind je notaties een beetje vaag dus dat is lastig te lezen zo. De kettingregel is trouwens geen definitie, maar kan je gewoon bewijzen vanuit de definitie van de afgeleide. Ik vind de opgave sowieso vreemd dat je infinitesimalen moet uitdrukken in andere infinitesimalen...


Oke dat dacht ik inderdaad ook, ik zal eens even kijken of ik de notatie wat makkelijker kan maken *moment*quote:Op zondag 7 augustus 2011 12:25 schreef thenxero het volgende:
dz/dx = 2 x u + x² du/dx
Ik vind je notaties een beetje vaag dus dat is lastig te lezen zo. De kettingregel is trouwens geen definitie, maar kan je gewoon bewijzen vanuit de definitie van de afgeleide. Ik vind de opgave sowieso vreemd dat je infinitesimalen moet uitdrukken in andere infinitesimalen...


Oh of bedoel je met dx dy en dz soms de afgeleiden naar x, y resp z?
En met z'x de afgeleide van z naar x?
En met z'x de afgeleide van z naar x?


met dx bedoel ik een (kleine) verandering van x. (of tenminste, zo bedoelt het boek het)quote:Op zondag 7 augustus 2011 12:42 schreef thenxero het volgende:
Oh of bedoel je met dx dy en dz soms de afgeleiden naar x, y resp z?
En met z'x de afgeleide van z naar x?
met z'x bedoel ik inderdaad de afgeleide van z naar x.


Het lukt me niet om het in mooiere syntax weer te geven.
[ Bericht 92% gewijzigd door JohnSpek op 07-08-2011 13:46:47 ]
[ Bericht 92% gewijzigd door JohnSpek op 07-08-2011 13:46:47 ]


Dat klopt niet, jij doet de breuk tot de vijfde macht en dan staat er wat anders.quote:Op zondag 7 augustus 2011 11:23 schreef maen het volgende:
Ok, ik begrijp dat je die eerste met 5 kunt vermenigvuldigen, maar ik kom dan op
q1-4q23
3q1q2-2
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


ow, oeps. Maar met die machten hoef ik dan niets te doen?quote:Op zondag 7 augustus 2011 13:42 schreef GlowMouse het volgende:
[..]
Dat klopt niet, jij doet de breuk tot de vijfde macht en dan staat er wat anders.


Het gaat fout als jij hier z'x gaat bepalen: je moet u dan als constant beschouwen.quote:Op zondag 7 augustus 2011 11:46 schreef JohnSpek het volgende:
Ik heb de volgende opdracht:
syntax = u'x = du/dx
"Find dz expressed in terms of dx and dy when u = u(x,y)."
z = (x^2)*u
Ik gebruik de definitie dz = (z'x) * (dx) + (z'u) * (du)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Als je teller en noemer keer vijf doet dan blijft er hetzelfde staan (maar ben je de 1/5 kwijt en 3/5 wordt 3). De machten blijven wel hetzelfde. Wat Nelis89 zegt dus.quote:Op zondag 7 augustus 2011 13:49 schreef maen het volgende:
[..]
ow, oeps. Maar met die machten hoef ik dan niets te doen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


ah, dan weet ik waar het mis gegaan is. danku!quote:Op zondag 7 augustus 2011 13:54 schreef GlowMouse het volgende:
[..]
Als je teller en noemer keer vijf doet dan blijft er hetzelfde staan (maar ben je de 1/5 kwijt en 3/5 wordt 3). De machten blijven wel hetzelfde. Wat Nelis89 zegt dus.


Ik vermoed dat ik weet waar ik fout ga:quote:Op zondag 7 augustus 2011 13:52 schreef GlowMouse het volgende:
[..]
Het gaat fout als jij hier z'x gaat bepalen: je moet u dan als constant beschouwen.
bij de formule dz = z'x * dx + z'u * du
Hier is z'x de partiële afgeleide van z naar u, waar je u dan constant houdt ook al is u een functie van x.
De regel die ik gebruikte om z'x te bepalen (z'x = (z'x)* (x') + (z'u) * (u'x)) is een regel voor de totale afgeleide van z naar x toe, dus niet de partiële.
De definitie z'x = (z'x)* (x') + (z'u) * (u'x) zegt dus:
De totale afgeleide van z naar x = de partiele afgeleide van z naar x * afgeleide van x naar x + de partiele afgeleide van z naar y * afgeleide van u naar x.
Klopt dit wat ik nu zeg?


Held!quote:Op vrijdag 29 juli 2011 21:48 schreef GlowMouse het volgende:
Vanaf nu kun je met de [tex]-tag Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).


Zie nu pas dat we latex kunnen gebruiken! Erg mooi, Glowmouse!
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Ik ben bezig met een wiskunde opfriscursus en ben nu bij het onderwerp differentieren beland. Ik heb het vroeger allemaal gehad en had er nooit problemen mee, maar er is een vraag die ik niet echt begrijp.
Hij luidt als volgt:
Voor de differentieerbare functie f geldt dat:
f(x) = 10x^2 + 2x + 5 als x ≤ 1.
Voor x>1 geldt dat f(x)=a⋅x+b voor constanten a en b.
Wat zijn de waarden van a en b? Wat is het functievoorschrift f(x) voor x>1?
Voor x>1 geldt f(x)= [hier je antwoord]
Bij 'tips' staat het volgende over dit 'probleem':
Kies de waarden van a en b zo, dat in het punt x=1 de functie 10⋅x2+2⋅x+5
en a⋅x+b dezelfde waarde aannemen en dezelfde afgeleide hebben.
En de oplossing is:
Voor x groter dan 1 is de vergelijking
f(x)=22⋅x+−5.
Ik weet hier echt niet wat ze precies bedoelen en vroeger op het vwo had ik ook nooit zoiets gehad, het was altijd simpelweg een formule krijgen en daar moest je dan de afgeleide van bepalen.
Mijn vraag gaat dus niet zozeer over hoe je moet differentieren en wat de regels daarbij zijn, maar meer over wat er hier bedoeld wordt.
Bij voorbaat dank!
PS: het is een online cursus dus ik heb geen leraar aan wie ik het kan vragen.
Hij luidt als volgt:
Voor de differentieerbare functie f geldt dat:
f(x) = 10x^2 + 2x + 5 als x ≤ 1.
Voor x>1 geldt dat f(x)=a⋅x+b voor constanten a en b.
Wat zijn de waarden van a en b? Wat is het functievoorschrift f(x) voor x>1?
Voor x>1 geldt f(x)= [hier je antwoord]
Bij 'tips' staat het volgende over dit 'probleem':
Kies de waarden van a en b zo, dat in het punt x=1 de functie 10⋅x2+2⋅x+5
en a⋅x+b dezelfde waarde aannemen en dezelfde afgeleide hebben.
En de oplossing is:
Voor x groter dan 1 is de vergelijking
f(x)=22⋅x+−5.
Ik weet hier echt niet wat ze precies bedoelen en vroeger op het vwo had ik ook nooit zoiets gehad, het was altijd simpelweg een formule krijgen en daar moest je dan de afgeleide van bepalen.
Mijn vraag gaat dus niet zozeer over hoe je moet differentieren en wat de regels daarbij zijn, maar meer over wat er hier bedoeld wordt.
Bij voorbaat dank!
PS: het is een online cursus dus ik heb geen leraar aan wie ik het kan vragen.


Wat ze dus willen is dat je je constanten a en b zodanig kiest dat de functies f(x) = 10x^2 + 2x + 5 en ax+b naadloos op elkaar aansluiten. Even officiëler gezegd, dat er aan de continuïteits- èn differentieerbaarheidsvoorwaaden voldaan wordt op het punt P(1,17)
we hebben f(x) = 10x^2 + 2x + 5; dit geeft als afgeleide f '(x) = 20x + 2
we hebben ook f(x) = ax+b; dit geeft als afgeleide simpelweg f '(x) = a
Eerst gaan we aan de slag met de afgeleiden; we nemen de linkerlimiet van 20x + 2 voor x -> 1 => 20*1 + 2 = 22. Hieruit kun je direct concluderen dat de constante a in de functie f(x) = ax+b dus 22 moet zijn; after all, f '(x) = a = 22.
nu we weten dat a = 22, kunnen de oorspronkelijke functies onder handen nemen. We nemen wederom de linkerlimiet, dit keer van 10x^2 + 2x + 5 voor x -> 1 => f(x) = 17
nu pluggen we alles in a*x +b = y in.
a = 22 (je richtingscoëfficiënt die adhv je afgeleiden bepaald hebt)
x = 1 (dat is de x-coördinaat van het punt waar de functies naadloos op elkaar moeten aansluiten)
y = 22 (kan je direct berekenen door in f(x) de waarde 1 in te vullen)
22*1 + b = 17 => b = -5
[ Bericht 19% gewijzigd door VanishedEntity op 14-08-2011 21:01:41 ]
we hebben f(x) = 10x^2 + 2x + 5; dit geeft als afgeleide f '(x) = 20x + 2
we hebben ook f(x) = ax+b; dit geeft als afgeleide simpelweg f '(x) = a
Eerst gaan we aan de slag met de afgeleiden; we nemen de linkerlimiet van 20x + 2 voor x -> 1 => 20*1 + 2 = 22. Hieruit kun je direct concluderen dat de constante a in de functie f(x) = ax+b dus 22 moet zijn; after all, f '(x) = a = 22.
nu we weten dat a = 22, kunnen de oorspronkelijke functies onder handen nemen. We nemen wederom de linkerlimiet, dit keer van 10x^2 + 2x + 5 voor x -> 1 => f(x) = 17
nu pluggen we alles in a*x +b = y in.
a = 22 (je richtingscoëfficiënt die adhv je afgeleiden bepaald hebt)
x = 1 (dat is de x-coördinaat van het punt waar de functies naadloos op elkaar moeten aansluiten)
y = 22 (kan je direct berekenen door in f(x) de waarde 1 in te vullen)
22*1 + b = 17 => b = -5
[ Bericht 19% gewijzigd door VanishedEntity op 14-08-2011 21:01:41 ]


Maar de vraag doet toch een heleboel aannames? Waarom kan x > 1 niet gewoon een andere richtingscoëfficiënt hebben?


Er staat "differentieerbare functie". Deze samengestelde functie f(x) = 10x^2 + 2x + 5 voor x ≤ 1 EN f(x) = ax+b voor x>1 moet in het punt P(1, 17):quote:Op zondag 14 augustus 2011 20:39 schreef JohnSpek het volgende:
Maar de vraag doet toch een heleboel aannames? Waarom kan x > 1 niet gewoon een andere richtingscoëfficiënt hebben?
- zowel continu ( lim x↑1 f(x) = lim x↓1 f(x) )
- als differentieerbaar (lim x↑1 f '(x) = lim x↓1 f '(x) )
zijn.
[ Bericht 0% gewijzigd door VanishedEntity op 14-08-2011 21:01:29 ]


Nee, zoals VE al aangaf maar dan simpeler verwoord: de functie heeft dan in het punt x=1 een knak en is daar dan niet diff'baar. Verder moet je ervoor zorgen dat de functie na x=1 geen sprongetje maakt, want dan is hij niet meer continu en dus niet meer differentieerbaar (differentieerbaarheid impliceert continuïteit). Met die twee voorwaarden van gelijke afgeleide en gelijke functiewaarde in het punt 1 kan je dus a en b afleiden.quote:Op zondag 14 augustus 2011 20:39 schreef JohnSpek het volgende:
Maar de vraag doet toch een heleboel aannames? Waarom kan x > 1 niet gewoon een andere richtingscoëfficiënt hebben?


Je moet gewoon zorgen dat 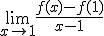 bestaat.
bestaat.
Je notatie is raar, maar je lijkt hier continu differentieerbaar te schrijven, en dat is een strengere eis.quote:Op zondag 14 augustus 2011 20:56 schreef VanishedEntity het volgende:
[..]
- als differentieerbaar (lim x↑1 f '(x) = lim x↓1 f '(x) )
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


En dat doe je door zowel de linkerlimiet als de rechterlimiet te berekenen en te verifiëren dat die 2 uitkomsten aan elkaar gelijk zijn.quote:
Ik weet niet wat jouw probleem is maar lim x↑a voor de linkerlimiet en lim x↓a voor de rechterlimiet zijn echt heel gebruikelijke notaties (pakt zn Wiskunde B examen en samenvattingen boekje er nog eens bij). En dr staan echt wel accenten bij de f-jes op de regel die de differentieerbaarheidseis vermeldt.quote:Je notatie is raar, maar je lijkt hier continu differentieerbaar te schrijven, en dat is een strengere eis.


Oh, het is subscript. De 1 lijkt bij mij veel op een pijltje omhoog. Je eist nu dat de afgeleide continu is, en dat is meer dan differentieerbaarheid alleen; zie voor een voorbeeld http://en.wikipedia.org/w(...)rentiability_classes
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


In het punt waar de functie van het ene voorschift in het andere voorschift overgaat (in dit geval x=1 => P(1,17) ) moet hij volgens de opgave zowel continu als differentieerbaar zijn. Wat de functievoorschriften in punten voor andere waarden van x en daarmee y doen is niet van belang.quote:Op zondag 14 augustus 2011 22:59 schreef GlowMouse het volgende:
Oh, het is subscript. De 1 lijkt bij mij veel op een pijltje omhoog. Je eist nu dat de afgeleide continu is, en dat is meer dan differentieerbaarheid alleen; zie voor een voorbeeld http://en.wikipedia.org/w(...)rentiability_classes


Precies, maar de afgeleide zelf hoeft niet continu te zijn.quote:Op zondag 14 augustus 2011 23:06 schreef VanishedEntity het volgende:
[..]
In het punt waar de functie van het ene voorschift in het andere voorschift overgaat (in dit geval x=1 => P(1,17) ) moet hij volgens de opgave zowel continu als differentieerbaar zijn. Wat de functievoorschriften in punten voor andere waarden van x en daarmee y doen is niet van belang.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Vandaar dat ik de eisen ook voor alleen x=1 geformuleerd hebquote:Op zondag 14 augustus 2011 23:13 schreef GlowMouse het volgende:
[..]
Precies, maar de afgeleide zelf hoeft niet continu te zijn.


Continuïteit hoeft niet op een domein te slaan, je hebt ook continuïteit in een punt. En een afgeleide hoeft niet continu te zijn in een punt om er te bestaan, zoals het voorbeeld op wikipedia aantoont.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik kom ergens niet uit, ik kan het wel beredeneren maar niet wiskundig oplossen:
a – 3 = 97 en a * 0,03 = 3 (die 3 heb ik zelf verzonnen, 3 kan je ook vervangen door bijvoorbeeld b)
Ik weet dan: 100 – 3 = 97, 100 x 0,03 = 3 en 100 – (100 x 0,03) = 97
Maar hoe kan ik dit wiskundig oplossen?
0,03 = (a – 97)/a --->
0,03a = (a – 97) en dan?
Moet dit via trail-and-error of is er wel een oplossing voor? Het gaat om een opgave uit de levensverzekeringswiskunde waarbij lx-dx=lx+1 en lx*qx = dx
[ Bericht 2% gewijzigd door dikkefriet op 16-08-2011 19:59:50 ]
a – 3 = 97 en a * 0,03 = 3 (die 3 heb ik zelf verzonnen, 3 kan je ook vervangen door bijvoorbeeld b)
Ik weet dan: 100 – 3 = 97, 100 x 0,03 = 3 en 100 – (100 x 0,03) = 97
Maar hoe kan ik dit wiskundig oplossen?
0,03 = (a – 97)/a --->
0,03a = (a – 97) en dan?
Moet dit via trail-and-error of is er wel een oplossing voor? Het gaat om een opgave uit de levensverzekeringswiskunde waarbij lx-dx=lx+1 en lx*qx = dx
[ Bericht 2% gewijzigd door dikkefriet op 16-08-2011 19:59:50 ]


Twee onafhankelijke vergelijkingen met 1 onbekende?
Die kan je gewoon apart oplossen, maar echt veel tussenstappen kan je niet opschrijven.
Ik snap nog niet precies waar je heen wil?
Die kan je gewoon apart oplossen, maar echt veel tussenstappen kan je niet opschrijven.
Ik snap nog niet precies waar je heen wil?
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Zoiets?
1a) a - 3 = 97
1b) a - 3 + 3 = 97 + 3
1c) a + 0 = 100
1d) a = 100
2a) a * 0.03 = 3
2b) (a * 0.03) / 0.03 = 3 / 0.03
2c) a * (0.03 / 0.03) = 3 / (3/100) = (3*100) / 3 = 100
2d) a = 100
1a) a - 3 = 97
1b) a - 3 + 3 = 97 + 3
1c) a + 0 = 100
1d) a = 100
2a) a * 0.03 = 3
2b) (a * 0.03) / 0.03 = 3 / 0.03
2c) a * (0.03 / 0.03) = 3 / (3/100) = (3*100) / 3 = 100
2d) a = 100


Sorry ik was een x vergeten te edditen in een a.
0,03 = (a – 97)/a --->
0,03a = (a – 97) en dan?
Ik kan zien dat a = 100, maar hoe kan je dit berekenen?
Argh, nu snap ik er zelf niets meer van.
Opnieuw: je weet lx-dx=lx+1 en lx*qx = dx.
Je weet l21 = 48979, q20=0.0601565. Vraag: berekend l20.
Ik kwam niet verder dan: l20 - (l20*0.0601565) = 48.979
[ Bericht 45% gewijzigd door dikkefriet op 16-08-2011 20:05:36 ]
0,03 = (a – 97)/a --->
0,03a = (a – 97) en dan?
Ik kan zien dat a = 100, maar hoe kan je dit berekenen?
Argh, nu snap ik er zelf niets meer van.
Opnieuw: je weet lx-dx=lx+1 en lx*qx = dx.
Je weet l21 = 48979, q20=0.0601565. Vraag: berekend l20.
Ik kwam niet verder dan: l20 - (l20*0.0601565) = 48.979
[ Bericht 45% gewijzigd door dikkefriet op 16-08-2011 20:05:36 ]


Wat wil je nou? Heb je mijn post gezien?quote:Op dinsdag 16 augustus 2011 19:56 schreef dikkefriet het volgende:
Sorry ik was een x vergeten te edditen in een a.
0,03 = (a – 97)/a --->
0,03a = (a – 97) en dan?
Ik kan zien dat a = 100, maar hoe kan je dit berekenen?


0.03 = (a - 97)/a
0.03 = 1 - 97/a
-0.97 = - 97/a
a = -97/-0.97 = 100
Bedoel je dat?
0.03 = 1 - 97/a
-0.97 = - 97/a
a = -97/-0.97 = 100
Bedoel je dat?
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]


Bedankt Nelis89, dat bedoel ik.
Hoe kan je van (a - 97) naar 1 - 97 gaan? Je haalt de haakjes weg en vervangt de a door een 1.
Hoe kan je van (a - 97) naar 1 - 97 gaan? Je haalt de haakjes weg en vervangt de a door een 1.


Als je a – 3 = 97 hebt, doen jullie wel moeilijk 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dat krijg je als je vage vragen steltquote:Op dinsdag 16 augustus 2011 20:34 schreef GlowMouse het volgende:
Als je a – 3 = 97 hebt, doen jullie wel moeilijk


Hoi kan iemand me laten zien hoe je de eigenwaarden van deze matrix efficient kunt vinden?
Ik moet op een karakteristieke vergelijking zien uit te komen en die dan oplossen.
[ Bericht 9% gewijzigd door Hondenbrokken op 19-08-2011 16:54:34 ]
| 1 2 3 | 4 & 1 & -3 // 2 & 3 & -3 // 2 & 1 & -1 |
Ik moet op een karakteristieke vergelijking zien uit te komen en die dan oplossen.
[ Bericht 9% gewijzigd door Hondenbrokken op 19-08-2011 16:54:34 ]
Jesus hates you.


Je zoekt drie getallen waarvan de som 6, en het product 8 is (spoor en determinant).
Noem de matrix A. Er geldt det(A-cI) = (4-c)((3-c)(-1-c)+3) - 1(2(-1-c)+6) - 3(2-2(3-c)) = -c³+6c²-12c+8. Één nulpunt wordt gegeven door c=2, en door (c-2) buiten haakjes te halen krijg je nog twee oplossingen c=2.
Noem de matrix A. Er geldt det(A-cI) = (4-c)((3-c)(-1-c)+3) - 1(2(-1-c)+6) - 3(2-2(3-c)) = -c³+6c²-12c+8. Één nulpunt wordt gegeven door c=2, en door (c-2) buiten haakjes te halen krijg je nog twee oplossingen c=2.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bij mij gaat het steeds fout als ik die determinant probeer te vereenvoudigen.quote:Op vrijdag 19 augustus 2011 16:55 schreef GlowMouse het volgende:
Je zoekt drie getallen waarvan de som 6, en het product 8 is (spoor en determinant).
Noem de matrix A. Er geldt det(A-cI) = (4-c)((3-c)(-1-c)+3) - 1(2(-1-c)+6) - 3(2-2(3-c)) = -c³+6c²-12c+8. Één nulpunt wordt gegeven door c=2, en door (c-2) buiten haakjes te halen krijg je nog twee oplossingen c=2.
Jesus hates you.


Waarom moet ik juist daarnaar zoeken? Wat is precies het idee erachter?quote:Je zoekt drie getallen waarvan de som 6, en het product 8 is (spoor en determinant).
Ik heb gegoogeld op spoor, maar ik kon alleen vinden dat de spoor gedefinieerd is als de som van de diagonaal, dus de spoor zou dan 8 - 3c zijn.
Zoals jij het zegt, klinkt het als een gewone kwadratische vergelijking, terwijl er een derdemacht is.
Jesus hates you.


Spoor van A. Bij een 2x2 matrix is dat een hele snelle methode, bij een 3x3 heb je alsnog det A-cI nodig.quote:Op vrijdag 19 augustus 2011 17:40 schreef Hondenbrokken het volgende:
[..]
Waarom moet ik juist daarnaar zoeken? Wat is precies het idee erachter?
Ik heb gegoogeld op spoor, maar ik kon alleen vinden dat de spoor gedefinieerd is als de som van de diagonaal, dus de spoor zou dan 8 - 3c zijn.
Zoals jij het zegt, klinkt het als een gewone kwadratische vergelijking, terwijl er een derdemacht is.
Je ziet zo dat x=-1 een oplossing is.quote:Op zaterdag 20 augustus 2011 18:48 schreef Hondenbrokken het volgende:
Hoe los je dan x^3 - (3/4)x + 1/4 = 0 op met spoor en determinant?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Stel ik heb de lineaire afbeelding f: V-->V en Im fk=im fk+1Dan maak ik de beperking op f met afbeelding g: Im fk --> V met v|-->f(v).
Dat g injectief is zie ik, maar g is toch niet surjectief (en dus isomorf)?
Dat g injectief is zie ik, maar g is toch niet surjectief (en dus isomorf)?


Neem f(x) = 0 voor iedere x in V = R. Het is een lineaire afbeelding want f(ax) = 0 = a f(x) en f(x+y) = 0 = f(x) + f(y). Im f = {0} en f(f(x)) = 0 voor alle x en dus ook Im f^2 = 0, dus Im f^k = {0} dus Im f^k = Im f^{k+1} voor alle k. De ristrictie g is nu gewoon g(0)=f(0)=0 dus Im g = {0} =! R = V. Dus g is inderdaad niet surjectief.


Aha, zo had ik er niet naar gekeken.quote:Op zondag 14 augustus 2011 22:02 schreef thenxero het volgende:
[..]
Nee, zoals VE al aangaf maar dan simpeler verwoord: de functie heeft dan in het punt x=1 een knak en is daar dan niet diff'baar. Verder moet je ervoor zorgen dat de functie na x=1 geen sprongetje maakt, want dan is hij niet meer continu en dus niet meer differentieerbaar (differentieerbaarheid impliceert continuïteit). Met die twee voorwaarden van gelijke afgeleide en gelijke functiewaarde in het punt 1 kan je dus a en b afleiden.


Ik denk dat ik deze vraag uit examen-paniek stelde (dan kan ik geen onduidelijk gebruik van het woord isomorfisme gebruiken!).quote:Op dinsdag 23 augustus 2011 21:07 schreef thenxero het volgende:
Neem f(x) = 0 voor iedere x in V = R. Het is een lineaire afbeelding want f(ax) = 0 = a f(x) en f(x+y) = 0 = f(x) + f(y). Im f = {0} en f(f(x)) = 0 voor alle x en dus ook Im f^2 = 0, dus Im f^k = {0} dus Im f^k = Im f^{k+1} voor alle k. De ristrictie g is nu gewoon g(0)=f(0)=0 dus Im g = {0} =! R = V. Dus g is inderdaad niet surjectief.
Hoe dan ook bedankt.


Oke, ik heb morgen een tentamen getaltheorie en ik verwacht hier geen antwoord voor die tijd, maar ik probeer het toch maar:
Hoe bepaald je de orde van de klassen in de ideaalklassengroep?
De elementen van de ideaalklassengroep kan ik bepalen met een algoritme en dan vind ik bijvoorbeeld het element: Z + Z(sqrt(-62)) in Z[\sqrt(-62)]
Hoe weet ik wat de orde van dat element is?
Oja, ik deze post vaak editten met meer vragen
Hoe bepaald je de orde van de klassen in de ideaalklassengroep?
De elementen van de ideaalklassengroep kan ik bepalen met een algoritme en dan vind ik bijvoorbeeld het element: Z + Z(sqrt(-62)) in Z[\sqrt(-62)]
Hoe weet ik wat de orde van dat element is?
Oja, ik deze post vaak editten met meer vragen


quote:Op donderdag 25 augustus 2011 21:45 schreef marleenhoofd- het volgende:
Oke, ik heb morgen een tentamen getaltheorie en ik verwacht hier geen antwoord voor die tijd, maar ik probeer het toch maar:
Hoe bepaald je de orde van de klassen in de ideaalklassengroep?
De elementen van de ideaalklassengroep kan ik bepalen met een algoritme en dan vind ik bijvoorbeeld het element: Z + Z(sqrt(-62)) in Z[\sqrt(-62)]
Hoe weet ik wat de orde van dat element is?
Oja, ik deze post vaak editten met meer vragen


Dat is waar, sorry niet zo'n snugger voorbeeld. Hoe doe je het dan bij een element als Z6+Z(-2+\sqrt(-62))?


Ik denk het niet en ik zou ook niet zo goed weten hoe... (nee, ik weet ook niet helemaal waar ik mee bezig ben)


ow wacht, ik heb wel een getal bepaald zodat elke ideaal een element bevat met de norm kleiner dan dat getal keer de norm van het ideaal. Bedoel je dat?
Dat getal is in dit geval 9
Minkowski zei me tot nog toe niks en met zijn wikipedia komt ik nog niet veel verder..
Dat getal is in dit geval 9
Minkowski zei me tot nog toe niks en met zijn wikipedia komt ik nog niet veel verder..


In dat geval is het ook zo dat elke ideaalklasse een ideaal van norm kleiner dan 9 bevat. (Opgave: bewijs dit).


Oke, hett element is a en het ideaal A, dan N(a)<=9N(A). (a) zit in A dus er is een B met (a)=ABquote:Op donderdag 25 augustus 2011 22:23 schreef thabit het volgende:
In dat geval is het ook zo dat elke ideaalklasse een ideaal van norm kleiner dan 9 bevat. (Opgave: bewijs dit).
N(a)=N(A)N(B)<=9N(A), dus N(B)<=9
Nu moet ik alleen nog het verband met het bepalen van de orde zien..
[ Bericht 0% gewijzigd door marleenhoofd- op 25-08-2011 22:45:11 ]


Daarbij bedenk ik me dat ik het nemen van normen van idealen en van elementen misschien door de war haal. De norm van een ideaal is gedefinieerd als het aantal elementen van de ring met het ideaal weggedeeld.
Mag ik dan voor het uitrekenen van de norm van (1+\sqrt(-62)) gewoon (1+\sqrt(-62)) (1-\sqrt(-62)) =63 doen? Vast niet zeker..
Edit: dit lijkt me toch wel te kloppen..
[ Bericht 6% gewijzigd door marleenhoofd- op 25-08-2011 22:52:29 ]
Mag ik dan voor het uitrekenen van de norm van (1+\sqrt(-62)) gewoon (1+\sqrt(-62)) (1-\sqrt(-62)) =63 doen? Vast niet zeker..
Edit: dit lijkt me toch wel te kloppen..
[ Bericht 6% gewijzigd door marleenhoofd- op 25-08-2011 22:52:29 ]


Bedankt in ieder geval. Door je tips heb ik naar een aantal dingen gezocht die mijn inzicht over waarom alles zo werkt wel wat vergroot hebben.
Ik ga nu slapen en morgen vroeg op, hopend dat ik misschien nog wat heldere inzichten krijg.
[ Bericht 89% gewijzigd door marleenhoofd- op 25-08-2011 23:34:05 ]
Ik ga nu slapen en morgen vroeg op, hopend dat ik misschien nog wat heldere inzichten krijg.
[ Bericht 89% gewijzigd door marleenhoofd- op 25-08-2011 23:34:05 ]


Ja dat mag wel. En de norm van I kun je als volgt uitrekenen:quote:Op donderdag 25 augustus 2011 22:42 schreef marleenhoofd- het volgende:
Daarbij bedenk ik me dat ik het nemen van normen van idealen en van elementen misschien door de war haal. De norm van een ideaal is gedefinieerd als het aantal elementen van de ring met het ideaal weggedeeld.
Mag ik dan voor het uitrekenen van de norm van (1+\sqrt(-62)) gewoon (1+\sqrt(-62)) (1-\sqrt(-62)) =63 doen? Vast niet zeker..
Edit: dit lijkt me toch wel te kloppen..
dus de norm is 6.
[ Bericht 2% gewijzigd door thabit op 26-08-2011 10:27:16 ]


newlines kunnen niet in een tex-tag, ik kan eens kijken of het wel zou werken
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


De \\ werkt binnen de tag sowieso wel om dingen op een nieuwe regel te krijgen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Kort vraagje,
Ik heb een opgave in Wiskunde B waarin de notatie d(N, AB) staat. De opgave is bewijs dat de bissectrices van een driehoek elkaar snijden..
Maargoed, N is dan het snijpunt van de bissectrices door 2 hoeken, en het snijpunt is N
"k en l snijden elkaar in N.
N op k dus d(N, AB) = .......
k is de bissectrice door hoek A, l door hoek B.
De vraag is simpel, wat houdt d(N, AB) in?
Ik heb een opgave in Wiskunde B waarin de notatie d(N, AB) staat. De opgave is bewijs dat de bissectrices van een driehoek elkaar snijden..
Maargoed, N is dan het snijpunt van de bissectrices door 2 hoeken, en het snijpunt is N
"k en l snijden elkaar in N.
N op k dus d(N, AB) = .......
k is de bissectrice door hoek A, l door hoek B.
De vraag is simpel, wat houdt d(N, AB) in?


