SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Ik heb een vraag over projectieve meetkunde. In het specifiek over de cross ratio. De cross ratio is invariant onder projectieve transformaties.Het is niet de enige invariant, want bv (cros ratio)^2 is ook invariant onder projectieve transformaties. Hoe bewijs ik de volgende stelling: Elke invariant van 4 punten is een functie van de cross ratio.
Ik gebruik de volgende definitie; cross ratio: [p,q;r,s]=(r-p)*(s-q)/(r-q)*(s-p). Alle hulp is welkom.
Ik gebruik de volgende definitie; cross ratio: [p,q;r,s]=(r-p)*(s-q)/(r-q)*(s-p). Alle hulp is welkom.
-


Het Nederlandse woord voor "cross ratio" is "dubbelverhouding". Je zou het volgende kunnen bewijzen. Gegeven twee viertallen punten met dezelfde dubbelverhouding, bestaat er een projectieve transformatie die het ene viertal in het andere overvoert.quote:Op vrijdag 29 juli 2011 21:17 schreef gaussie het volgende:
Ik heb een vraag over projectieve meetkunde. In het specifiek over de cross ratio. De cross ratio is invariant onder projectieve transformaties.Het is niet de enige invariant, want bv (cros ratio)^2 is ook invariant onder projectieve transformaties. Hoe bewijs ik de volgende stelling: Elke invariant van 4 punten is een functie van de cross ratio.
Ik gebruik de volgende definitie; cross ratio: [p,q;r,s]=(r-p)*(s-q)/(r-q)*(s-p). Alle hulp is welkom.


Vanaf nu kun je met de [tex]-tag Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
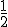
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hey hey,
Ik ben op zoek naar handige constructies/voorbeelden (met de hand en/of met Magma) van krommen en morfismen met de volgende eigenschappen:
 is een kromme over
is een kromme over 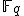 van geslacht
van geslacht 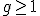 en er is een morfisme
en er is een morfisme 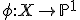 van graad
van graad 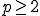 met de eigenschap
met de eigenschap 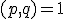 en
en 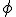 is Galois over
is Galois over 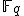 : Er is een automorfisme
: Er is een automorfisme 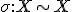 van orde
van orde  gedefinieerd over
gedefinieerd over 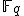 met
met 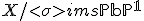 .
.
Alvast heeeeeeeeeeeeeeeeeeeeeeeeel veeeeel dank.
[ Bericht 0% gewijzigd door morfine2011 op 30-07-2011 13:30:10 ]
Ik ben op zoek naar handige constructies/voorbeelden (met de hand en/of met Magma) van krommen en morfismen met de volgende eigenschappen:
Alvast heeeeeeeeeeeeeeeeeeeeeeeeel veeeeel dank.
[ Bericht 0% gewijzigd door morfine2011 op 30-07-2011 13:30:10 ]


Kudo!!!quote:Op vrijdag 29 juli 2011 21:48 schreef GlowMouse het volgende:
Vanaf nu kun je met de [tex]-tag Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).


wat ben ik blij dat ik mijn algebra-vakken al ooit heb gehaald.. Sterkte ermee.quote:Op zaterdag 30 juli 2011 13:24 schreef morfine2011 het volgende:
Hey hey,
Ik ben op zoek naar handige constructies/voorbeelden (met de hand en/of met Magma) van krommen en morfismen met de volgende eigenschappen:is een kromme over
van geslacht
en er is een morfisme
van graad
met de eigenschap
en
is Galois over
: Er is een automorfisme
van orde
gedefinieerd over
met
.
Alvast heeeeeeeeeeeeeeeeeeeeeeeeel veeeeel dank.


quote:Op maandag 1 augustus 2011 14:59 schreef Don_Vanelli het volgende:
[..]
wat ben ik blij dat ik mijn algebra-vakken al ooit heb gehaald.. Sterkte ermee.


Ik denk dat het handiger is om de vraag iets preciezer te stellen; wat wil je nu eigenlijk weten?quote:Op zaterdag 30 juli 2011 13:24 schreef morfine2011 het volgende:
Hey hey,
Ik ben op zoek naar handige constructies/voorbeelden (met de hand en/of met Magma) van krommen en morfismen met de volgende eigenschappen:is een kromme over
van geslacht
en er is een morfisme
van graad
met de eigenschap
en
is Galois over
: Er is een automorfisme
van orde
gedefinieerd over
met
.
Alvast heeeeeeeeeeeeeeeeeeeeeeeeel veeeeel dank.
Het moet denk ik wel mogelijk zijn om met klassenlichamentheorie aan de slag te gaan en op die manier cyclische uitbreidingen van Fq(t) te construeren (wel oppassen dat je het constantenlichaam gelijk aan Fq houdt). Wegens de voorwaarde (p,q)=1 zal alles ook nog eens tam vertakt zijn. Als je enkel veel voorbeelden wenst te vinden, kun je je concentreren op gevallen waarin weinig (bijvoorbeeld 3) punten vertakt zijn.
Er zal vast ook wel wat literatuur te vinden zijn over dit probleem, wat in feite neerkomt op een generalisatie van Kronecker-Weber naar het geval van functielichamen.


Wat ik eigenlijk deed en wil doen kan ik het best illustreren met een voorbeeld:
Eerst maak ik een kromme:
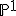
de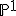 .
.
 bepaal ik de bijbehorende vezel.
bepaal ik de bijbehorende vezel.
 een
een 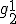 linear systeem die door
linear systeem die door 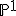 geparametriseerd wordt. Zo geldt:
geparametriseerd wordt. Zo geldt:
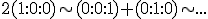
(ik hoef niet perse te eisen dat (p,q)=1).
Merk op dat de pullbacks van de rationale punten rationale punten zijn...
Wat ik boven gedaan heb, wil ik doen voor krommen met bijv. een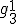 linear systeem die over
linear systeem die over 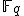 gedefinieerd is. Een manier om dus zulke lineaire systemen te vinden is een morfisme te maken naar
gedefinieerd is. Een manier om dus zulke lineaire systemen te vinden is een morfisme te maken naar 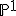 en dan kijken naar de pullbacks van rationale punten op
en dan kijken naar de pullbacks van rationale punten op 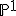 .
.
Een idee is te kijken naar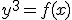 over
over 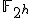 Het lukt me niet om alleen rationale pullbacks te krijgen..... en daar zit ik dus vast mee.
Het lukt me niet om alleen rationale pullbacks te krijgen..... en daar zit ik dus vast mee.
Eerst maak ik een kromme:
en dan eenquote:F<w>:=GF(2^2);
K<x,y,z>:=PolynomialRing(F,3);
f:=x^2*y+w*y^2*z+w^2*z^2*x;
X:=Curve(ProjectiveSpace(F,2),f);
Daarna bepaal ik de plaatsen en definieer ik een morfisme van mijn kromme naarquote:Y:=Curve(ProjectiveSpace(F,1));
de
Nu komt het: voor ieder punt uitquote:plcsY:=Places(Y,1);
phi:=map<X->Y|[x,y]>;
phi;
De uitvoer behorende bij de laatste quote is:quote:L:=[];
for i:=1 to #plcsY do L[i]:= Decomposition(Pullback(phi,plcsY[i])); end for;
L;
In feite er is opquote:[
[
<Place at (1 : 0 : 0), 2>
],
[
<Place at (0 : 0 : 1), 1>,
<Place at (0 : 1 : 0), 1>
],
[
<Place at (w : 1 : 1), 1>,
<Place at (w^2 : w : 1), 1>
],
[
<Place at (1 : w : 1), 1>,
<Place at (w : w^2 : 1), 1>
],
[
<Place at (1 : 1 : 1), 1>,
<Place at (w^2 : w^2 : 1), 1>
]
]
(ik hoef niet perse te eisen dat (p,q)=1).
Merk op dat de pullbacks van de rationale punten rationale punten zijn...
Wat ik boven gedaan heb, wil ik doen voor krommen met bijv. een
Een idee is te kijken naar


Ja omdat onder alle linear fractional transformations (dus van de vorm f(x)=ax+b/cx+d) de dubbelverhouding hetzelfde blijft. Dus met andere woorden [f(p),f(q),f(r),f(s)]=[p,q,r,s]. Hoe nu verder?quote:Op vrijdag 29 juli 2011 21:27 schreef thabit het volgende:
[..]
Het Nederlandse woord voor "cross ratio" is "dubbelverhouding". Je zou het volgende kunnen bewijzen. Gegeven twee viertallen punten met dezelfde dubbelverhouding, bestaat er een projectieve transformatie die het ene viertal in het andere overvoert.
-


Ook in het voorbeeld is het niet zo dat van alle rationale punten de inverse beelden uit rationale punten bestaan. Alleen degenen waarvan je al weet dat er een rationaal punt boven ligt. Aangezien de graad 2 is, blijft er weinig keus over voor het andere punt. Dus ik snap nog steeds niet helemaal wat je vraag nu precies is.quote:Op dinsdag 2 augustus 2011 19:53 schreef morfine2011 het volgende:
Wat ik eigenlijk deed en wil doen kan ik het best illustreren met een voorbeeld:
Eerst maak ik een kromme:
[..]
en dan een
[..]
Daarna bepaal ik de plaatsen en definieer ik een morfisme van mijn kromme naar
de.
[..]
Nu komt het: voor ieder punt uitbepaal ik de bijbehorende vezel.
[..]
De uitvoer behorende bij de laatste quote is:
[..]
In feite er is opeen
linear systeem die door
geparametriseerd wordt. Zo geldt:
(ik hoef niet perse te eisen dat (p,q)=1).
Merk op dat de pullbacks van de rationale punten rationale punten zijn...
Wat ik boven gedaan heb, wil ik doen voor krommen met bijv. eenlinear systeem die over
gedefinieerd is. Een manier om dus zulke lineaire systemen te vinden is een morfisme te maken naar
en dan kijken naar de pullbacks van rationale punten op
.
Een idee is te kijken naarover
Het lukt me niet om alleen rationale pullbacks te krijgen..... en daar zit ik dus vast mee.


Wel, je kan bijvoorbeeld gebruiken dat je elk drietal verschillende punten op 0, 1, en oneindig kan afbeelden dmv een gebroken lineaire transformatie.quote:Op dinsdag 2 augustus 2011 21:48 schreef gaussie het volgende:
[..]
Ja omdat onder alle linear fractional transformations (dus van de vorm f(x)=ax+b/cx+d) de dubbelverhouding hetzelfde blijft. Dus met andere woorden [f(p),f(q),f(r),f(s)]=[p,q,r,s]. Hoe nu verder?


Iets duidelijker: ik wil een kromme X en een afbeelding naar P^1 kunnen maken met de eigenschap dat als een rationaal punt op P^1 een rationaal punt heeft in de vezel dan zijn de overige punten in die vezel ook rationaal. Dus een generalisatie van het geval wat ik boven heb beschreven: i.p.v een morfisme van graad 2, wil ik het voor graad 3 of een hoger priem graad doen, hier is X van geslacht min 3.quote:. Alleen degenen waarvan je al weet dat er een rationaal punt boven ligt. Aangezien de graad 2 is, blijft er weinig keus over voor het andere punt.


Even wat gebrainstorm:
Stel K=Fq(X) en neem aan dat K/Fq(t) separabel is. Zij L de Galoisafsluiting van K over Fq(t) en laat G de Galoisgroep zijn, die we zien als permutatiegroep op de verzameling Hom(K, L) van lichaamsinbeddingen van K in L over Fq(t).
Als we een rationaal punt hebben, dan is dat een element waarop Frobq triviaal werkt. Frobq werkt ook op de vezel waarin dat punt ligt. Is deze vezel onvertakt, dan kunnen we Frobq liften naar een element g van G; het cykeltype dat g op de vezel heeft is hetzelfde als op Hom(K, L).
Het lijkt dus handig als de permutatiegroep G aan de volgende eigenschap voldoet: het triviale element is het enige element met een dekpunt. Als dat zo is, dan zal dus (behalve misschien in vertakte vezels) aan het probleem voldaan zijn; niet alleen over Fq, maar ook over elke uitbreiding daarvan.
Er zijn meer voorbeelden van zulke G dan alleen cyclische groepen. Als G bijvoorbeeld op zichzelf werkt middels een Cayley-actie, dan ben je er ook (kortom als K Galois is over Fq(t)).
Anderzijds is het gemiddeld aantal dekpunten van de elementen van een eindige permutatiegroep altijd gelijk aan het aantal banen, dus gelijk aan 1 in ons geval. Als K/Fq(t) niet Galois is, dan zal G groter zijn dan de verzameling waarop ze werkt en dus niet-triviale elementen met dekpunten bevatten. Kortom, de groep G zal aan de gewenste eigenschap voldoen desda K/Fq(t) Galois is.
Uiteraard kunnen er ook voorbeelden bestaan waarin G niet aan deze eigenschap voldoet; dan heb je gewoon simpelweg het resultaat niet voor elke willekeurige uitbreiding van Fq. De constructie van zulke voorbeelden zal wel wat ingewikkelder zijn.
Er is wel het een en ander geschreven over het zoeken naar polynomen met gegeven Galoisgroepen, in elk geval over lichamen zoals Q en Q(t), maar ook wel over andere lichamen. De resultaten over Q(t) zou je misschien kunnen hanteren en dan hopen dat er nog wat van de Galoisgroep overblijft als je de coëfficiënten naar Fq reduceert. Misschien is er in de volgende boeken wat te vinden:
Jensen, Ledet, Yui - Generic Polynomials: Constructive Aspects of the Inverse Galois Problem
Malle & Matzat - Inverse Galois Theory
Serre - Topics in Galois Theory
Stel K=Fq(X) en neem aan dat K/Fq(t) separabel is. Zij L de Galoisafsluiting van K over Fq(t) en laat G de Galoisgroep zijn, die we zien als permutatiegroep op de verzameling Hom(K, L) van lichaamsinbeddingen van K in L over Fq(t).
Als we een rationaal punt hebben, dan is dat een element waarop Frobq triviaal werkt. Frobq werkt ook op de vezel waarin dat punt ligt. Is deze vezel onvertakt, dan kunnen we Frobq liften naar een element g van G; het cykeltype dat g op de vezel heeft is hetzelfde als op Hom(K, L).
Het lijkt dus handig als de permutatiegroep G aan de volgende eigenschap voldoet: het triviale element is het enige element met een dekpunt. Als dat zo is, dan zal dus (behalve misschien in vertakte vezels) aan het probleem voldaan zijn; niet alleen over Fq, maar ook over elke uitbreiding daarvan.
Er zijn meer voorbeelden van zulke G dan alleen cyclische groepen. Als G bijvoorbeeld op zichzelf werkt middels een Cayley-actie, dan ben je er ook (kortom als K Galois is over Fq(t)).
Anderzijds is het gemiddeld aantal dekpunten van de elementen van een eindige permutatiegroep altijd gelijk aan het aantal banen, dus gelijk aan 1 in ons geval. Als K/Fq(t) niet Galois is, dan zal G groter zijn dan de verzameling waarop ze werkt en dus niet-triviale elementen met dekpunten bevatten. Kortom, de groep G zal aan de gewenste eigenschap voldoen desda K/Fq(t) Galois is.
Uiteraard kunnen er ook voorbeelden bestaan waarin G niet aan deze eigenschap voldoet; dan heb je gewoon simpelweg het resultaat niet voor elke willekeurige uitbreiding van Fq. De constructie van zulke voorbeelden zal wel wat ingewikkelder zijn.
Er is wel het een en ander geschreven over het zoeken naar polynomen met gegeven Galoisgroepen, in elk geval over lichamen zoals Q en Q(t), maar ook wel over andere lichamen. De resultaten over Q(t) zou je misschien kunnen hanteren en dan hopen dat er nog wat van de Galoisgroep overblijft als je de coëfficiënten naar Fq reduceert. Misschien is er in de volgende boeken wat te vinden:
Jensen, Ledet, Yui - Generic Polynomials: Constructive Aspects of the Inverse Galois Problem
Malle & Matzat - Inverse Galois Theory
Serre - Topics in Galois Theory


Bedankt voor de uitleg,quote:Op dinsdag 26 juli 2011 02:03 schreef Riparius het volgende:
[..]
Bekijk het eens als volgt. De cosinus en de sinus zijn periodieke functies met een periode 2π. Dat betekent dus dat:
(1) cos(3/2∙π + α) = cos (α - 1/2∙π)
Je weet ook dat de cosinusfunctie een even functie is, i.e. cos(-θ) = cos θ, en dus:
(2) cos (α - 1/2∙π) = cos (1/2∙π - α)
Nu is de cosinus van een hoek gelijk aan de sinus van het complement (daar komt ook de naam cosinus vandaan), dus:
(3) cos (1/2∙π - α) = sin α
Uit (1), (2) en (3) volgt uiteraard dat cos(3/2∙π + α) = sin α
Met een tekening is dit ook te zien aan de hand van de eenheidscirkel. Kies een punt op de eenheidscirkel boven de x-as, en noem de hoek van de radius naar dat punt met de positieve x-as α, dan is de sinus van die hoek positief, de sinus van α is immers per definitie de y-coördinaat van het beeldpunt van (1;0) bij een rotatie over een hoek α om de oorsprong. Doe je er nu 3/2∙π bij, dan kom je uit op een punt op de eenheidscirkel in de rechter helft van het vlak, aangezien 3/2∙π rad correspondeert met 3/4 van de omtrek van de eenheidscirkel. Ik denk dat je over het hoofd ziet dat de cosinus van een hoek (c.q. rotatie) per definitie de x-coördinaat is van het beeldpunt van (1;0) bij een rotatie om de oorsprong. En de x-coördinaat van een punt rechts van de y-as is positief. Ergo, als sin α positief is, dan moet cos(α + 3/2∙π) ook positief zijn, en omgekeerd. Je kunt dus ook zonder herleidingen meteen inzien dat cos(α + 3/2π) niet gelijk kan zijn aan -sin α.
Ik heb net na terugkomst van de vakantie de som opnieuw gedaan en het simpelweg uitgetekend mbv een eenheidscirkel, en now it all makes sense!.....stom dat ik het niet inzag.
Nogmaals bedankt!


Ik vroeg mij af hoe jullie al die kennis van wiskunde in het hoofd blijven houden. Tijdens het leren van nieuwe theorieën vergeet ik vaak de oude en blijven enkel de regels zitten. Hierdoor begrijp ik de nieuwe theorie vaak niet zo goed.
Ik ben nu bijvoorbeeld bezig met het uitrekenen van varianties met matricen. In deze theorie gebruiken ze getransponeerde matricen. Ik herinner mij dan nog wel dat
(A*B)^t (^t = transpose) gelijk staat aan (B^t)*(A^t), maar niet waarom dat ook alweer is. Ik heb het echter wel ooit gesnapt. Hierdoor verlies ik een hoop inzicht van de nieuwe theorie.
[ Bericht 2% gewijzigd door JohnSpek op 04-08-2011 19:55:43 ]
Ik ben nu bijvoorbeeld bezig met het uitrekenen van varianties met matricen. In deze theorie gebruiken ze getransponeerde matricen. Ik herinner mij dan nog wel dat
(A*B)^t (^t = transpose) gelijk staat aan (B^t)*(A^t), maar niet waarom dat ook alweer is. Ik heb het echter wel ooit gesnapt. Hierdoor verlies ik een hoop inzicht van de nieuwe theorie.
[ Bericht 2% gewijzigd door JohnSpek op 04-08-2011 19:55:43 ]


Veel bewijzen uit het eerste jaar kan ik nu zo opschrijven omdat ze helemaal niet zo lastig zijn. Af en toe kijk ik terug, en af en toe maakt het mij niet uit. Jouw transposevoorbeeld zou ik zo uitschrijven door te kijken waaraan element (i,j) gelijk is, maar die moeite zou ik niet nemen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je zou die transposeregel even snel kunnen checken met twee 2x2 matrices bijvoorbeeld, zodat je wat meer inzicht hebt hoe het in elkaar zit. Dat kan je dan algemeen gaan opschrijven maar dat is gewoon geen leuk klusje. 


Valt wel mee, één regeltje met 3 gelijkheidstekens.quote:Op donderdag 4 augustus 2011 21:09 schreef thenxero het volgende:
Dat kan je dan algemeen gaan opschrijven maar dat is gewoon geen leuk klusje.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Klopt maar het klooien met indices of matrixelementen vind/vond ik nooit leukquote:Op donderdag 4 augustus 2011 21:11 schreef GlowMouse het volgende:
[..]
Valt wel mee, één regeltje met 3 gelijkheidstekens.

