SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Ik ben bezig met een wiskunde opfriscursus en ben nu bij het onderwerp differentieren beland. Ik heb het vroeger allemaal gehad en had er nooit problemen mee, maar er is een vraag die ik niet echt begrijp.
Hij luidt als volgt:
Voor de differentieerbare functie f geldt dat:
f(x) = 10x^2 + 2x + 5 als x ≤ 1.
Voor x>1 geldt dat f(x)=a⋅x+b voor constanten a en b.
Wat zijn de waarden van a en b? Wat is het functievoorschrift f(x) voor x>1?
Voor x>1 geldt f(x)= [hier je antwoord]
Bij 'tips' staat het volgende over dit 'probleem':
Kies de waarden van a en b zo, dat in het punt x=1 de functie 10⋅x2+2⋅x+5
en a⋅x+b dezelfde waarde aannemen en dezelfde afgeleide hebben.
En de oplossing is:
Voor x groter dan 1 is de vergelijking
f(x)=22⋅x+−5.
Ik weet hier echt niet wat ze precies bedoelen en vroeger op het vwo had ik ook nooit zoiets gehad, het was altijd simpelweg een formule krijgen en daar moest je dan de afgeleide van bepalen.
Mijn vraag gaat dus niet zozeer over hoe je moet differentieren en wat de regels daarbij zijn, maar meer over wat er hier bedoeld wordt.
Bij voorbaat dank!
PS: het is een online cursus dus ik heb geen leraar aan wie ik het kan vragen.
Hij luidt als volgt:
Voor de differentieerbare functie f geldt dat:
f(x) = 10x^2 + 2x + 5 als x ≤ 1.
Voor x>1 geldt dat f(x)=a⋅x+b voor constanten a en b.
Wat zijn de waarden van a en b? Wat is het functievoorschrift f(x) voor x>1?
Voor x>1 geldt f(x)= [hier je antwoord]
Bij 'tips' staat het volgende over dit 'probleem':
Kies de waarden van a en b zo, dat in het punt x=1 de functie 10⋅x2+2⋅x+5
en a⋅x+b dezelfde waarde aannemen en dezelfde afgeleide hebben.
En de oplossing is:
Voor x groter dan 1 is de vergelijking
f(x)=22⋅x+−5.
Ik weet hier echt niet wat ze precies bedoelen en vroeger op het vwo had ik ook nooit zoiets gehad, het was altijd simpelweg een formule krijgen en daar moest je dan de afgeleide van bepalen.
Mijn vraag gaat dus niet zozeer over hoe je moet differentieren en wat de regels daarbij zijn, maar meer over wat er hier bedoeld wordt.
Bij voorbaat dank!
PS: het is een online cursus dus ik heb geen leraar aan wie ik het kan vragen.
Wat ze dus willen is dat je je constanten a en b zodanig kiest dat de functies f(x) = 10x^2 + 2x + 5 en ax+b naadloos op elkaar aansluiten. Even officiëler gezegd, dat er aan de continuïteits- èn differentieerbaarheidsvoorwaaden voldaan wordt op het punt P(1,17)
we hebben f(x) = 10x^2 + 2x + 5; dit geeft als afgeleide f '(x) = 20x + 2
we hebben ook f(x) = ax+b; dit geeft als afgeleide simpelweg f '(x) = a
Eerst gaan we aan de slag met de afgeleiden; we nemen de linkerlimiet van 20x + 2 voor x -> 1 => 20*1 + 2 = 22. Hieruit kun je direct concluderen dat de constante a in de functie f(x) = ax+b dus 22 moet zijn; after all, f '(x) = a = 22.
nu we weten dat a = 22, kunnen de oorspronkelijke functies onder handen nemen. We nemen wederom de linkerlimiet, dit keer van 10x^2 + 2x + 5 voor x -> 1 => f(x) = 17
nu pluggen we alles in a*x +b = y in.
a = 22 (je richtingscoëfficiënt die adhv je afgeleiden bepaald hebt)
x = 1 (dat is de x-coördinaat van het punt waar de functies naadloos op elkaar moeten aansluiten)
y = 22 (kan je direct berekenen door in f(x) de waarde 1 in te vullen)
22*1 + b = 17 => b = -5
[ Bericht 19% gewijzigd door VanishedEntity op 14-08-2011 21:01:41 ]
we hebben f(x) = 10x^2 + 2x + 5; dit geeft als afgeleide f '(x) = 20x + 2
we hebben ook f(x) = ax+b; dit geeft als afgeleide simpelweg f '(x) = a
Eerst gaan we aan de slag met de afgeleiden; we nemen de linkerlimiet van 20x + 2 voor x -> 1 => 20*1 + 2 = 22. Hieruit kun je direct concluderen dat de constante a in de functie f(x) = ax+b dus 22 moet zijn; after all, f '(x) = a = 22.
nu we weten dat a = 22, kunnen de oorspronkelijke functies onder handen nemen. We nemen wederom de linkerlimiet, dit keer van 10x^2 + 2x + 5 voor x -> 1 => f(x) = 17
nu pluggen we alles in a*x +b = y in.
a = 22 (je richtingscoëfficiënt die adhv je afgeleiden bepaald hebt)
x = 1 (dat is de x-coördinaat van het punt waar de functies naadloos op elkaar moeten aansluiten)
y = 22 (kan je direct berekenen door in f(x) de waarde 1 in te vullen)
22*1 + b = 17 => b = -5
[ Bericht 19% gewijzigd door VanishedEntity op 14-08-2011 21:01:41 ]
Maar de vraag doet toch een heleboel aannames? Waarom kan x > 1 niet gewoon een andere richtingscoëfficiënt hebben?
Er staat "differentieerbare functie". Deze samengestelde functie f(x) = 10x^2 + 2x + 5 voor x ≤ 1 EN f(x) = ax+b voor x>1 moet in het punt P(1, 17):quote:Op zondag 14 augustus 2011 20:39 schreef JohnSpek het volgende:
Maar de vraag doet toch een heleboel aannames? Waarom kan x > 1 niet gewoon een andere richtingscoëfficiënt hebben?
- zowel continu ( lim x↑1 f(x) = lim x↓1 f(x) )
- als differentieerbaar (lim x↑1 f '(x) = lim x↓1 f '(x) )
zijn.
[ Bericht 0% gewijzigd door VanishedEntity op 14-08-2011 21:01:29 ]
Nee, zoals VE al aangaf maar dan simpeler verwoord: de functie heeft dan in het punt x=1 een knak en is daar dan niet diff'baar. Verder moet je ervoor zorgen dat de functie na x=1 geen sprongetje maakt, want dan is hij niet meer continu en dus niet meer differentieerbaar (differentieerbaarheid impliceert continuïteit). Met die twee voorwaarden van gelijke afgeleide en gelijke functiewaarde in het punt 1 kan je dus a en b afleiden.quote:
Maar de vraag doet toch een heleboel aannames? Waarom kan x > 1 niet gewoon een andere richtingscoëfficiënt hebben?
Je moet gewoon zorgen dat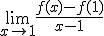 
bestaat.
Je notatie is raar, maar je lijkt hier continu differentieerbaar te schrijven, en dat is een strengere eis.quote:
[..]
- als differentieerbaar (lim x↑1 f '(x) = lim x↓1 f '(x) )
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
En dat doe je door zowel de linkerlimiet als de rechterlimiet te berekenen en te verifiëren dat die 2 uitkomsten aan elkaar gelijk zijn.quote:
Ik weet niet wat jouw probleem is maar lim x↑a voor de linkerlimiet en lim x↓a voor de rechterlimiet zijn echt heel gebruikelijke notaties (pakt zn Wiskunde B examen en samenvattingen boekje er nog eens bij). En dr staan echt wel accenten bij de f-jes op de regel die de differentieerbaarheidseis vermeldt.quote:Je notatie is raar, maar je lijkt hier continu differentieerbaar te schrijven, en dat is een strengere eis.
Oh, het is subscript. De 1 lijkt bij mij veel op een pijltje omhoog. Je eist nu dat de afgeleide continu is, en dat is meer dan differentieerbaarheid alleen; zie voor een voorbeeld http://en.wikipedia.org/w(...)rentiability_classes
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
In het punt waar de functie van het ene voorschift in het andere voorschift overgaat (in dit geval x=1 => P(1,17) ) moet hij volgens de opgave zowel continu als differentieerbaar zijn. Wat de functievoorschriften in punten voor andere waarden van x en daarmee y doen is niet van belang.quote:
Oh, het is subscript. De 1 lijkt bij mij veel op een pijltje omhoog. Je eist nu dat de afgeleide continu is, en dat is meer dan differentieerbaarheid alleen; zie voor een voorbeeld http://en.wikipedia.org/w(...)rentiability_classes
Precies, maar de afgeleide zelf hoeft niet continu te zijn.quote:
[..]
In het punt waar de functie van het ene voorschift in het andere voorschift overgaat (in dit geval x=1 => P(1,17) ) moet hij volgens de opgave zowel continu als differentieerbaar zijn. Wat de functievoorschriften in punten voor andere waarden van x en daarmee y doen is niet van belang.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Vandaar dat ik de eisen ook voor alleen x=1 geformuleerd hebquote:
[..]
Precies, maar de afgeleide zelf hoeft niet continu te zijn.
.
Continuïteit hoeft niet op een domein te slaan, je hebt ook continuïteit in een punt. En een afgeleide hoeft niet continu te zijn in een punt om er te bestaan, zoals het voorbeeld op wikipedia aantoont.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik kom ergens niet uit, ik kan het wel beredeneren maar niet wiskundig oplossen:
a – 3 = 97 en a * 0,03 = 3 (die 3 heb ik zelf verzonnen, 3 kan je ook vervangen door bijvoorbeeld b)
Ik weet dan: 100 – 3 = 97, 100 x 0,03 = 3 en 100 – (100 x 0,03) = 97
Maar hoe kan ik dit wiskundig oplossen?
0,03 = (a – 97)/a --->
0,03a = (a – 97) en dan?
Moet dit via trail-and-error of is er wel een oplossing voor? Het gaat om een opgave uit de levensverzekeringswiskunde waarbij lx-dx=lx+1 en lx*qx = dx
[ Bericht 2% gewijzigd door dikkefriet op 16-08-2011 19:59:50 ]
a – 3 = 97 en a * 0,03 = 3 (die 3 heb ik zelf verzonnen, 3 kan je ook vervangen door bijvoorbeeld b)
Ik weet dan: 100 – 3 = 97, 100 x 0,03 = 3 en 100 – (100 x 0,03) = 97
Maar hoe kan ik dit wiskundig oplossen?
0,03 = (a – 97)/a --->
0,03a = (a – 97) en dan?
Moet dit via trail-and-error of is er wel een oplossing voor? Het gaat om een opgave uit de levensverzekeringswiskunde waarbij lx-dx=lx+1 en lx*qx = dx
[ Bericht 2% gewijzigd door dikkefriet op 16-08-2011 19:59:50 ]
Twee onafhankelijke vergelijkingen met 1 onbekende?
Die kan je gewoon apart oplossen, maar echt veel tussenstappen kan je niet opschrijven.
Ik snap nog niet precies waar je heen wil?
Die kan je gewoon apart oplossen, maar echt veel tussenstappen kan je niet opschrijven.
Ik snap nog niet precies waar je heen wil?
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Zoiets?
1a) a - 3 = 97
1b) a - 3 + 3 = 97 + 3
1c) a + 0 = 100
1d) a = 100
2a) a * 0.03 = 3
2b) (a * 0.03) / 0.03 = 3 / 0.03
2c) a * (0.03 / 0.03) = 3 / (3/100) = (3*100) / 3 = 100
2d) a = 100
1a) a - 3 = 97
1b) a - 3 + 3 = 97 + 3
1c) a + 0 = 100
1d) a = 100
2a) a * 0.03 = 3
2b) (a * 0.03) / 0.03 = 3 / 0.03
2c) a * (0.03 / 0.03) = 3 / (3/100) = (3*100) / 3 = 100
2d) a = 100
Sorry ik was een x vergeten te edditen in een a.
0,03 = (a – 97)/a --->
0,03a = (a – 97) en dan?
Ik kan zien dat a = 100, maar hoe kan je dit berekenen?
Argh, nu snap ik er zelf niets meer van.
Opnieuw: je weet lx-dx=lx+1 en lx*qx = dx.
Je weet l21 = 48979, q20=0.0601565. Vraag: berekend l20.
Ik kwam niet verder dan: l20 - (l20*0.0601565) = 48.979
[ Bericht 45% gewijzigd door dikkefriet op 16-08-2011 20:05:36 ]
0,03 = (a – 97)/a --->
0,03a = (a – 97) en dan?
Ik kan zien dat a = 100, maar hoe kan je dit berekenen?
Argh, nu snap ik er zelf niets meer van.
Opnieuw: je weet lx-dx=lx+1 en lx*qx = dx.
Je weet l21 = 48979, q20=0.0601565. Vraag: berekend l20.
Ik kwam niet verder dan: l20 - (l20*0.0601565) = 48.979
[ Bericht 45% gewijzigd door dikkefriet op 16-08-2011 20:05:36 ]
Wat wil je nou? Heb je mijn post gezien?quote:
Sorry ik was een x vergeten te edditen in een a.
0,03 = (a – 97)/a --->
0,03a = (a – 97) en dan?
Ik kan zien dat a = 100, maar hoe kan je dit berekenen?
0.03 = (a - 97)/a
0.03 = 1 - 97/a
-0.97 = - 97/a
a = -97/-0.97 = 100
Bedoel je dat?
0.03 = 1 - 97/a
-0.97 = - 97/a
a = -97/-0.97 = 100
Bedoel je dat?
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
Bedankt Nelis89, dat bedoel ik.
Hoe kan je van (a - 97) naar 1 - 97 gaan? Je haalt de haakjes weg en vervangt de a door een 1.
Hoe kan je van (a - 97) naar 1 - 97 gaan? Je haalt de haakjes weg en vervangt de a door een 1.
Als je a – 3 = 97 hebt, doen jullie wel moeilijk 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dat krijg je als je vage vragen steltquote:
Als je a – 3 = 97 hebt, doen jullie wel moeilijk
Hoi kan iemand me laten zien hoe je de eigenwaarden van deze matrix efficient kunt vinden?
Ik moet op een karakteristieke vergelijking zien uit te komen en die dan oplossen.
[ Bericht 9% gewijzigd door Hondenbrokken op 19-08-2011 16:54:34 ]
| 1 2 3 | 4 & 1 & -3 // 2 & 3 & -3 // 2 & 1 & -1 |
Ik moet op een karakteristieke vergelijking zien uit te komen en die dan oplossen.
[ Bericht 9% gewijzigd door Hondenbrokken op 19-08-2011 16:54:34 ]
Jesus hates you.
Je zoekt drie getallen waarvan de som 6, en het product 8 is (spoor en determinant).
Noem de matrix A. Er geldt det(A-cI) = (4-c)((3-c)(-1-c)+3) - 1(2(-1-c)+6) - 3(2-2(3-c)) = -c³+6c²-12c+8. Één nulpunt wordt gegeven door c=2, en door (c-2) buiten haakjes te halen krijg je nog twee oplossingen c=2.
Noem de matrix A. Er geldt det(A-cI) = (4-c)((3-c)(-1-c)+3) - 1(2(-1-c)+6) - 3(2-2(3-c)) = -c³+6c²-12c+8. Één nulpunt wordt gegeven door c=2, en door (c-2) buiten haakjes te halen krijg je nog twee oplossingen c=2.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Bij mij gaat het steeds fout als ik die determinant probeer te vereenvoudigen.quote:
Je zoekt drie getallen waarvan de som 6, en het product 8 is (spoor en determinant).
Noem de matrix A. Er geldt det(A-cI) = (4-c)((3-c)(-1-c)+3) - 1(2(-1-c)+6) - 3(2-2(3-c)) = -c³+6c²-12c+8. Één nulpunt wordt gegeven door c=2, en door (c-2) buiten haakjes te halen krijg je nog twee oplossingen c=2.
Jesus hates you.
Waarom moet ik juist daarnaar zoeken? Wat is precies het idee erachter?quote:Je zoekt drie getallen waarvan de som 6, en het product 8 is (spoor en determinant).
Ik heb gegoogeld op spoor, maar ik kon alleen vinden dat de spoor gedefinieerd is als de som van de diagonaal, dus de spoor zou dan 8 - 3c zijn.
Zoals jij het zegt, klinkt het als een gewone kwadratische vergelijking, terwijl er een derdemacht is.
Jesus hates you.
Spoor van A. Bij een 2x2 matrix is dat een hele snelle methode, bij een 3x3 heb je alsnog det A-cI nodig.quote:Op vrijdag 19 augustus 2011 17:40 schreef Hondenbrokken het volgende:
[..]
Waarom moet ik juist daarnaar zoeken? Wat is precies het idee erachter?
Ik heb gegoogeld op spoor, maar ik kon alleen vinden dat de spoor gedefinieerd is als de som van de diagonaal, dus de spoor zou dan 8 - 3c zijn.
Zoals jij het zegt, klinkt het als een gewone kwadratische vergelijking, terwijl er een derdemacht is.
Je ziet zo dat x=-1 een oplossing is.quote:
Hoe los je dan x^3 - (3/4)x + 1/4 = 0 op met spoor en determinant?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Stel ik heb de lineaire afbeelding f: V-->V en Im fk=im fk+1Dan maak ik de beperking op f met afbeelding g: Im fk --> V met v|-->f(v).
Dat g injectief is zie ik, maar g is toch niet surjectief (en dus isomorf)?
Dat g injectief is zie ik, maar g is toch niet surjectief (en dus isomorf)?
Neem f(x) = 0 voor iedere x in V = R. Het is een lineaire afbeelding want f(ax) = 0 = a f(x) en f(x+y) = 0 = f(x) + f(y). Im f = {0} en f(f(x)) = 0 voor alle x en dus ook Im f^2 = 0, dus Im f^k = {0} dus Im f^k = Im f^{k+1} voor alle k. De ristrictie g is nu gewoon g(0)=f(0)=0 dus Im g = {0} =! R = V. Dus g is inderdaad niet surjectief.
Aha, zo had ik er niet naar gekeken.quote:
[..]
Nee, zoals VE al aangaf maar dan simpeler verwoord: de functie heeft dan in het punt x=1 een knak en is daar dan niet diff'baar. Verder moet je ervoor zorgen dat de functie na x=1 geen sprongetje maakt, want dan is hij niet meer continu en dus niet meer differentieerbaar (differentieerbaarheid impliceert continuïteit). Met die twee voorwaarden van gelijke afgeleide en gelijke functiewaarde in het punt 1 kan je dus a en b afleiden.
Ik denk dat ik deze vraag uit examen-paniek stelde (dan kan ik geen onduidelijk gebruik van het woord isomorfisme gebruiken!).quote:
Neem f(x) = 0 voor iedere x in V = R. Het is een lineaire afbeelding want f(ax) = 0 = a f(x) en f(x+y) = 0 = f(x) + f(y). Im f = {0} en f(f(x)) = 0 voor alle x en dus ook Im f^2 = 0, dus Im f^k = {0} dus Im f^k = Im f^{k+1} voor alle k. De ristrictie g is nu gewoon g(0)=f(0)=0 dus Im g = {0} =! R = V. Dus g is inderdaad niet surjectief.
Hoe dan ook bedankt.
Oke, ik heb morgen een tentamen getaltheorie en ik verwacht hier geen antwoord voor die tijd, maar ik probeer het toch maar:
Hoe bepaald je de orde van de klassen in de ideaalklassengroep?
De elementen van de ideaalklassengroep kan ik bepalen met een algoritme en dan vind ik bijvoorbeeld het element: Z + Z(sqrt(-62)) in Z[\sqrt(-62)]
Hoe weet ik wat de orde van dat element is?
Oja, ik deze post vaak editten met meer vragen
Hoe bepaald je de orde van de klassen in de ideaalklassengroep?
De elementen van de ideaalklassengroep kan ik bepalen met een algoritme en dan vind ik bijvoorbeeld het element: Z + Z(sqrt(-62)) in Z[\sqrt(-62)]
Hoe weet ik wat de orde van dat element is?
Oja, ik deze post vaak editten met meer vragen
quote:
Oke, ik heb morgen een tentamen getaltheorie en ik verwacht hier geen antwoord voor die tijd, maar ik probeer het toch maar:
Hoe bepaald je de orde van de klassen in de ideaalklassengroep?
De elementen van de ideaalklassengroep kan ik bepalen met een algoritme en dan vind ik bijvoorbeeld het element: Z + Z(sqrt(-62)) in Z[\sqrt(-62)]
Hoe weet ik wat de orde van dat element is?
Oja, ik deze post vaak editten met meer vragen
Dat is waar, sorry niet zo'n snugger voorbeeld. Hoe doe je het dan bij een element als Z6+Z(-2+\sqrt(-62))?
Ik denk het niet en ik zou ook niet zo goed weten hoe... (nee, ik weet ook niet helemaal waar ik mee bezig ben)
ow wacht, ik heb wel een getal bepaald zodat elke ideaal een element bevat met de norm kleiner dan dat getal keer de norm van het ideaal. Bedoel je dat?
Dat getal is in dit geval 9
Minkowski zei me tot nog toe niks en met zijn wikipedia komt ik nog niet veel verder..
Dat getal is in dit geval 9
Minkowski zei me tot nog toe niks en met zijn wikipedia komt ik nog niet veel verder..
In dat geval is het ook zo dat elke ideaalklasse een ideaal van norm kleiner dan 9 bevat. (Opgave: bewijs dit).
Oke, hett element is a en het ideaal A, dan N(a)<=9N(A). (a) zit in A dus er is een B met (a)=ABquote:Op donderdag 25 augustus 2011 22:23 schreef thabit het volgende:
In dat geval is het ook zo dat elke ideaalklasse een ideaal van norm kleiner dan 9 bevat. (Opgave: bewijs dit).
N(a)=N(A)N(B)<=9N(A), dus N(B)<=9
Nu moet ik alleen nog het verband met het bepalen van de orde zien..
[ Bericht 0% gewijzigd door marleenhoofd- op 25-08-2011 22:45:11 ]
Daarbij bedenk ik me dat ik het nemen van normen van idealen en van elementen misschien door de war haal. De norm van een ideaal is gedefinieerd als het aantal elementen van de ring met het ideaal weggedeeld.
Mag ik dan voor het uitrekenen van de norm van (1+\sqrt(-62)) gewoon (1+\sqrt(-62)) (1-\sqrt(-62)) =63 doen? Vast niet zeker..
Edit: dit lijkt me toch wel te kloppen..
[ Bericht 6% gewijzigd door marleenhoofd- op 25-08-2011 22:52:29 ]
Mag ik dan voor het uitrekenen van de norm van (1+\sqrt(-62)) gewoon (1+\sqrt(-62)) (1-\sqrt(-62)) =63 doen? Vast niet zeker..
Edit: dit lijkt me toch wel te kloppen..
[ Bericht 6% gewijzigd door marleenhoofd- op 25-08-2011 22:52:29 ]
Bedankt in ieder geval. Door je tips heb ik naar een aantal dingen gezocht die mijn inzicht over waarom alles zo werkt wel wat vergroot hebben.
Ik ga nu slapen en morgen vroeg op, hopend dat ik misschien nog wat heldere inzichten krijg.
[ Bericht 89% gewijzigd door marleenhoofd- op 25-08-2011 23:34:05 ]
Ik ga nu slapen en morgen vroeg op, hopend dat ik misschien nog wat heldere inzichten krijg.
[ Bericht 89% gewijzigd door marleenhoofd- op 25-08-2011 23:34:05 ]
Ja dat mag wel. En de norm van I kun je als volgt uitrekenen:quote:
Daarbij bedenk ik me dat ik het nemen van normen van idealen en van elementen misschien door de war haal. De norm van een ideaal is gedefinieerd als het aantal elementen van de ring met het ideaal weggedeeld.
Mag ik dan voor het uitrekenen van de norm van (1+\sqrt(-62)) gewoon (1+\sqrt(-62)) (1-\sqrt(-62)) =63 doen? Vast niet zeker..
Edit: dit lijkt me toch wel te kloppen..
dus de norm is 6.
[ Bericht 2% gewijzigd door thabit op 26-08-2011 10:27:16 ]
newlines kunnen niet in een tex-tag, ik kan eens kijken of het wel zou werken
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
De \\ werkt binnen de tag sowieso wel om dingen op een nieuwe regel te krijgen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Kort vraagje,
Ik heb een opgave in Wiskunde B waarin de notatie d(N, AB) staat. De opgave is bewijs dat de bissectrices van een driehoek elkaar snijden..
Maargoed, N is dan het snijpunt van de bissectrices door 2 hoeken, en het snijpunt is N
"k en l snijden elkaar in N.
N op k dus d(N, AB) = .......
k is de bissectrice door hoek A, l door hoek B.
De vraag is simpel, wat houdt d(N, AB) in?
Ik heb een opgave in Wiskunde B waarin de notatie d(N, AB) staat. De opgave is bewijs dat de bissectrices van een driehoek elkaar snijden..
Maargoed, N is dan het snijpunt van de bissectrices door 2 hoeken, en het snijpunt is N
"k en l snijden elkaar in N.
N op k dus d(N, AB) = .......
k is de bissectrice door hoek A, l door hoek B.
De vraag is simpel, wat houdt d(N, AB) in?
