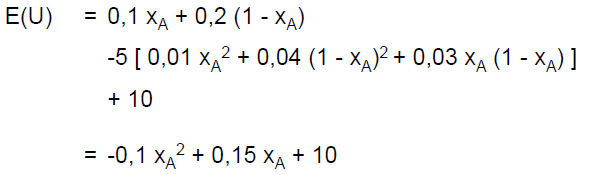SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
[ Bericht 14% gewijzigd door GlowMouse op 29-07-2011 21:46:30 ]
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
[ Bericht 14% gewijzigd door GlowMouse op 29-07-2011 21:46:30 ]
The biggest argument against democracy is a five minute discussion with the average voter.
Is goed.quote:Op maandag 11 juli 2011 13:26 schreef .aeon het volgende:
Zou iemand dit kunnen controleren?
[ afbeelding ]
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Oh ja. Dat is toch een tabel van 1 t/m 8 met de bijbehorende kansen die ik in de verwachtingswaarde heb gebruikt (1/32,3/32,..etc.)?
Precies. iia) kun je daarna makkelijker doen: de noemer is gewoon P(R) en die kun je makkelijker berekenen.quote:
Oh ja. Dat is toch een tabel van 1 t/m 8 met de bijbehorende kansen die ik in de verwachtingswaarde heb gebruikt (1/32,3/32,..etc.)?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ok, maar i) gaat over het maximum van de twee dobbelstenen, en ii) gaat over het aantal ogen van één van de dobbelstenen. Hoe zou je dit dan makkelijker kunnen doen?quote:Op maandag 11 juli 2011 13:56 schreef GlowMouse het volgende:
[..]
Precies. iia) kun je daarna makkelijker doen: de noemer is gewoon P(R) en die kun je makkelijker berekenen.
Zie ook in voor (ii)(b) dat:quote:
[..]
Ok, maar i) gaat over het maximum van de twee dobbelstenen, en ii) gaat over het aantal ogen van één van de dobbelstenen. Hoe zou je dit dan makkelijker kunnen doen?
P = 1 - P(Tc|R)n = 1 - (1 - P(T|R))n = 1 - (1/3)n
Zo is het eenvoudiger voor nog meer worpen en kun je aantonen dat voor n naar oneindig de kans nadert tot 1 dat je met de tetraëder hebt geworpen.
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
Nog een vraag over hetzelfde onderwerp:
Wat is de kans dat een goed antwoord op een multiple choice vraag (4 antwoordmogelijkheden) van een gokkende student afkomstig is, gegeven dat a) 10%, b) 50, c) 90% van de studenten gokt. d) Geef de kans voor een algemeen relatief aantal p van gokkende studenten.
a), b), en c) lukken me gemakkelijk op de manier die ik hierboven ook gebruikt heb. Daar krijg ik uit:
a) 10% = 1/28
b) 50% = 1/4
c) 90% = 3/4
Maar ik vind het moeilijk om daar een verband uit te halen?
Wat is de kans dat een goed antwoord op een multiple choice vraag (4 antwoordmogelijkheden) van een gokkende student afkomstig is, gegeven dat a) 10%, b) 50, c) 90% van de studenten gokt. d) Geef de kans voor een algemeen relatief aantal p van gokkende studenten.
a), b), en c) lukken me gemakkelijk op de manier die ik hierboven ook gebruikt heb. Daar krijg ik uit:
a) 10% = 1/28
b) 50% = 1/4
c) 90% = 3/4
Maar ik vind het moeilijk om daar een verband uit te halen?
ic, n/m.quote:
[..]
Ok, maar i) gaat over het maximum van de twee dobbelstenen, en ii) gaat over het aantal ogen van één van de dobbelstenen. Hoe zou je dit dan makkelijker kunnen doen?
pak gewoon je formule:quote:
Nog een vraag over hetzelfde onderwerp:
Wat is de kans dat een goed antwoord op een multiple choice vraag (4 antwoordmogelijkheden) van een gokkende student afkomstig is, gegeven dat a) 10%, b) 50, c) 90% van de studenten gokt. d) Geef de kans voor een algemeen relatief aantal p van gokkende studenten.
a), b), en c) lukken me gemakkelijk op de manier die ik hierboven ook gebruikt heb. Daar krijg ik uit:
a) 10% = 1/28
b) 50% = 1/4
c) 90% = 3/4
Maar ik vind het moeilijk om daar een verband uit te halen?
A is de gebeurtenis "antwoord is goed"
B is de gebeurtenis "student heeft gegokt"
P(B|A) = P(A|B)P(B) / [ P(A|B)P(B) + P(A|B')P(B') ] = p/4 / (p/4 + (1-p)) = p / (4 - 3p).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
400 - 31 = 150 - (x-4)
x-2 ..............x-4
Ik ben mijn wiskunde weer een beetje aan het opfrissen (en heb daar eerlijk gezegd reuze veel lol in), maar deze (zelfgemaakte) vergelijking is toch nog wat te moeilijk voor me. Ik weet dat x=10 (want: zelfgemaakt), maar kan dit niet laten zien door de vergelijking zo te versimpelen dat x=.... overblijft. Ik ben in staat om wat rond te schuiven met delen van de vergelijking, maar dan staan er steeds nog te veel x-en aan een kant van de vergelijking om er iets zinnigs over te zeggen.
Wie legt mij uit hoe ik deze vergelijking oplos? Voor de duidelijkheid, er staat: (400 / x-2) - 31 = (150 / x-4) - (x-4).
x-2 ..............x-4
Ik ben mijn wiskunde weer een beetje aan het opfrissen (en heb daar eerlijk gezegd reuze veel lol in), maar deze (zelfgemaakte) vergelijking is toch nog wat te moeilijk voor me. Ik weet dat x=10 (want: zelfgemaakt), maar kan dit niet laten zien door de vergelijking zo te versimpelen dat x=.... overblijft. Ik ben in staat om wat rond te schuiven met delen van de vergelijking, maar dan staan er steeds nog te veel x-en aan een kant van de vergelijking om er iets zinnigs over te zeggen.
Wie legt mij uit hoe ik deze vergelijking oplos? Voor de duidelijkheid, er staat: (400 / x-2) - 31 = (150 / x-4) - (x-4).
Begin eens met:quote:
400 - 31 = 150 - (x-4)
x-2 ..............x-4
Ik ben mijn wiskunde weer een beetje aan het opfrissen (en heb daar eerlijk gezegd reuze veel lol in), maar deze (zelfgemaakte) vergelijking is toch nog wat te moeilijk voor me. Ik weet dat x=10 (want: zelfgemaakt), maar kan dit niet laten zien door de vergelijking zo te versimpelen dat x=.... overblijft. Ik ben in staat om wat rond te schuiven met delen van de vergelijking, maar dan staan er steeds nog te veel x-en aan een kant van de vergelijking om er iets zinnigs over te zeggen.
Wie legt mij uit hoe ik deze vergelijking oplos? Voor de duidelijkheid, er staat: (400 / x-2) - 31 = (150 / x-4) - (x-4).
1) Rechts haakjes wegwerken
2) Breuken naar links
3) Getallen naar rechts
4) 1 breuk van maken links
Volgens mij moet je uiteindelijk wel een derdegraadspolynoom oplossen, dus het is niet echt een goed oefensommetje (tenzij je 3e graadspolynomen wil oefenen
).[ Bericht 5% gewijzigd door thenxero op 13-07-2011 15:28:46 ]
x=10 is inderdaad een antwoord, maar het probleem wordt een beetje dat x=(1/2)(31-sqrt(329)) en x=(1/2)(31+sqrt(329)) ook goede antwoorden zijn, dus waarschijnlijk niet helemaal het oefensommetje dat je zoekt zoals thenxero al zegt.
Polywatte?quote:
[..]
Begin eens met:
1) Rechts haakjes wegwerken
2) Breuken naar links
3) Getallen naar rechts
4) 1 breuk van maken links
Volgens mij moet je uiteindelijk wel een derdegraadspolynoom oplossen, dus het is niet echt een goed oefensommetje (tenzij je 3e graadspolynomen wil oefenen
Met je tips kom ik op:
(600/1,5x-3) - (600/4x-16) + (x-4) = 31.
X=10, en de vergelijking klopt dus nog steeds.
Hoe kan ik de breuken nu wegwerken?
Voor de uitwerking:quote:
400 - 31 = 150 - (x-4)
x-2 ..............x-4
Ik ben mijn wiskunde weer een beetje aan het opfrissen (en heb daar eerlijk gezegd reuze veel lol in), maar deze (zelfgemaakte) vergelijking is toch nog wat te moeilijk voor me. Ik weet dat x=10 (want: zelfgemaakt), maar kan dit niet laten zien door de vergelijking zo te versimpelen dat x=.... overblijft. Ik ben in staat om wat rond te schuiven met delen van de vergelijking, maar dan staan er steeds nog te veel x-en aan een kant van de vergelijking om er iets zinnigs over te zeggen.
Wie legt mij uit hoe ik deze vergelijking oplos? Voor de duidelijkheid, er staat: (400 / x-2) - 31 = (150 / x-4) - (x-4).
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
quote:
[..]
Voor de uitwerking:In die uitwerking gebruik je dus dat je weet dat x=10 een oplossing is. Dus daarom is het niet zo'n mooi sommetje.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Dat doet hij helemaal niet.quote:
[..]
In die uitwerking gebruik je dus dat je weet dat x=10 een oplossing is. Dus daarom is het niet zo'n mooi sommetje.
Gelijke noemers maken, zoals in de uitwerking hierbovenquote:
[..]
Polywatte?
Met je tips kom ik op:
(600/1,5x-3) - (600/4x-16) + (x-4) = 31.
X=10, en de vergelijking klopt dus nog steeds.
Hoe kan ik de breuken nu wegwerken?
. Polynoom = veelterm. Een derdegraadspolynoom is een veelterm van de vorm
a x^3 + b x^2 + c x + d = 0 . Derdegraads omdat 3 de grootste macht van x is.
Jawel hij factoriseert 10 eruit. Anders weet je niet dat je het kan schrijven als (x-10) * ietsquote:
quote:
[..]
Voor de uitwerking:Dank. Ik zit inderdaad way above my head.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
In dit geval wel, maar je kan het ook inzien. Maar je kan natuurlijk ook de formule van Cardano toepassenquote:
[..]
Jawel hij factoriseert 10 eruit. Anders weet je niet dat je het kan schrijven als (x-10) * iets
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
Tuurlijk, maar de vraagsteller wou juist op x=10 uitkomen, dat is een beetje het puntquote:
[..]
In dit geval wel, maar je kan het ook inzien. Maar je kan natuurlijk ook de formule van Cardano toepassen
Waarom? De herleiding is niet meer dan wat elementaire algebra. Dat zou je zonder meer moeten kunnen. Het wordt pas lastig ná de herleiding, als je een derdegraads vergelijking overhoudt.quote:
[..]
Dank. Ik zit inderdaad way above my head.
Als je de kleinste topologie op R hebt die alle intervallen van de vorm [a,b) bevat met a,b in R, wat is dan het interieur van (0,1] ?
Dat is dan de grootste open bevat in (0,1]. Opens in (0,1] zijn van de vorm [x,1), en x kan je dan willekeurig dicht naar nul laten gaan. Maar DE grootste verzameling van die vorm met x>0 bestaat niet, dus heeft (0,1] geen interieur? :S
Dat is dan de grootste open bevat in (0,1]. Opens in (0,1] zijn van de vorm [x,1), en x kan je dan willekeurig dicht naar nul laten gaan. Maar DE grootste verzameling van die vorm met x>0 bestaat niet, dus heeft (0,1] geen interieur? :S
Ah, die topologie heeft natuurlijk ook nog intervallen van de vorm (a,b). Want (a,b) = (Vereniging over n in N) [a+1/n, b), dus is (0,1) het interieur.quote:
Als je de kleinste topologie op R hebt die alle intervallen van de vorm [a,b) bevat met a,b in R, wat is dan het interieur van (0,1] ?
Dat is dan de grootste open bevat in (0,1]. Opens in (0,1] zijn van de vorm [x,1), en x kan je dan willekeurig dicht naar nul laten gaan. Maar DE grootste verzameling van die vorm met x>0 bestaat niet, dus heeft (0,1] geen interieur? :S
Die eerste stap is al fout. Hoe kom je daaraan?quote:
Ik doe iets heel fout de gehele tijd, maar ik kom niet op de -0.1xa^2 +0.15xa +10
[ afbeelding ]
Verkeerd gelezen
Het is een kwestie van netjes te werk gaan en alle haakjes wegwerken. Beetje veel om helemaal hier uit te gaan typen
.
Ik zal 't even voor je uitwerken en zo in deze post editen. Zit anders toch maar te wachtenquote:
Ik doe iets heel fout de gehele tijd, maar ik kom niet op de -0.1xa^2 +0.15xa +10
[ afbeelding ]
[ Bericht 53% gewijzigd door Djoezt op 16-07-2011 19:40:50 ]
Vraagje:
Ik zit wat opgaves te maken uit 'Basisboek Wiskunde' van Jan van de Craats:
de derde machtswortel van 375 in standaardvorm genoteerd is toch 3*derdemachtswortel 5?
Omdat 375/3=125=5^3?
In het boek staat 5*derdemachtswortel 3.
Doe ik iets verkeerd om?
Ik zit wat opgaves te maken uit 'Basisboek Wiskunde' van Jan van de Craats:
de derde machtswortel van 375 in standaardvorm genoteerd is toch 3*derdemachtswortel 5?
Omdat 375/3=125=5^3?
In het boek staat 5*derdemachtswortel 3.
Doe ik iets verkeerd om?
Je doet iets verkeerd om, maar dat is door je (gebrek aan) notatie niet meteen duidelijk.quote:
Vraagje:
Ik zit wat opgaves te maken uit 'Basisboek Wiskunde' van Jan van de Craats:
de derde machtswortel van 375 in standaardvorm genoteerd is toch 3*derdemachtswortel 5?
Omdat 375/3=125=5^3?
In het boek staat 5*derdemachtswortel 3.
We hebben:
(1) 375 = 3∙125 = 3∙53
En dus:
(2) ∛375 = ∛(3∙53) = ∛3∙∛(53) = 5∙∛3
Ik heb een vraag over projectieve meetkunde. Om precies te zijn over projecties van projectieve lijnen. Stel we hebben de volgende situatie. Neem O=(0,0) en veronderstel dat de lijn L1 parallel is aan de x-as en lijn L2 is parallel aan de y-as. Het punt O is equidistant aan beide lijnen. nu is het de bedoeling dat ik vanuit O, punten uit de lijn L1 projecteer op punten op de lijn L2. Dit gebeurt met behulp van de functie y=1/x. Het blijkt dat de beeld punten op lijn L2 convergeren. Naar het punt y=0. Dit correspondeert met de horizontale lijn door O. Het zogeheten point of infinity van de lijn L1. Mijn vraag is nu hoe kan vanuit de projectie uit O eerst het punt op lijn L1 bereikt worden en daarna pas het punt op L2? Want als ik naar het plaatje kijk dan ligt het punt op L2 voor het punt op L1. Deze situatie correspondeert met een rechte lijn door O die deze twee punten bevat. Meetkundig kan ik me dit niet voorstellen. Wellicht kan het te maken hebben met het feit dat projectieve lijnen eigenlijk cirkels zijn? Maar dan nog zie ik het niet voor me.
-
Hoe ziet, bij ANOVA (A1-A2 en B1-B2, een tabel en/of grafiek eruit met:
a) een interactie effect van A, maar geen hoofd-effect van B
b) een interactie effect, hoofd-effect van A, maar geen hoofd-effect van B
c) een interactie effect, maar geen hoofd-effect
(of zijn vraag a en b eigenlijk hetzelfde?)
a) een interactie effect van A, maar geen hoofd-effect van B
b) een interactie effect, hoofd-effect van A, maar geen hoofd-effect van B
c) een interactie effect, maar geen hoofd-effect
(of zijn vraag a en b eigenlijk hetzelfde?)
Herb is the healing of a nation, alcohol is the destruction.
Hoi ik zit met een vraag over wat vectoren. Het is volgens mij geen moeilijk probleem alleen zie ik het niet .
Ik heb een punt N(x,y,z) en een punt M(x,y,z). De genormaliseerde vector is een vector met lengte 1 (x,y,z). In dit plaatje dus (0,0,1).
Punt M-N levert een nieuwe vector op. Laten we deze a noemen.
Nu wil ik met deze informatie het punt O(x,y,z) bereken.
Als O-N een vector b is. Hoe reken ik dan dit punt uit? Hij moet dus gespiegeld worden over de genormaliseerde vector.
Hoop dat m'n vraag een beetje duidelijk is .
[ Bericht 3% gewijzigd door Dikbuik op 21-07-2011 13:50:51 ]
. Ik heb een punt N(x,y,z) en een punt M(x,y,z). De genormaliseerde vector is een vector met lengte 1 (x,y,z). In dit plaatje dus (0,0,1).
Punt M-N levert een nieuwe vector op. Laten we deze a noemen.
Nu wil ik met deze informatie het punt O(x,y,z) bereken.
Als O-N een vector b is. Hoe reken ik dan dit punt uit? Hij moet dus gespiegeld worden over de genormaliseerde vector.
Hoop dat m'n vraag een beetje duidelijk is
.
[ Bericht 3% gewijzigd door Dikbuik op 21-07-2011 13:50:51 ]
Omdat ImageShackquote:
Hoi ik zit met een vraag over wat vectoren. Het is volgens mij geen moeilijk probleem alleen zie ik het niet
Ik heb een punt N(x,y,z) en een punt M(x,y,z). De genormaliseerde vector is een vector met lengte 1 (x,y,z). In dit plaatje dus (0,0,1).
Punt M-N levert een nieuwe vector op. Laten we deze a noemen.
Nu wil ik met deze informatie het punt O(x,y,z) bereken.
Als O-N een vector b is. Hoe reken ik dan dit punt uit? Hij moet dus gespiegeld worden over de genormaliseerde vector.
Hoop dat m'n vraag een beetje duidelijk is
[ http://img35.imageshack.us/img35/1369/unledfjr.png (copy/paste deze link) ]
Krijg het plaatje hier niet werkend
Herb is the healing of a nation, alcohol is the destruction.
Ah okequote:
. Werkt nu.Weet nu dat ik een rotatiematrix moet maken alleen snap ik dit niet helemaal. Op de wiki hebben ze het namelijk over een rotatie om een x,y of z as, maar mijn normaalvector staat niet evenwijdig aan 1 van deze assen.
Dit wordt niks zo. Gebruik om te beginnen niet dezelfde variabelen voor de coördinaten van twee verschillende punten. Verder is je vraagstelling niet echt duidelijk. Je vraag helder formuleren is al de helft van de oplossing. Hint 1: het scalaire product van twee vectoren die loodrecht op elkaar staan is gelijk aan nul. Hint 2: het vectoriële product van twee vectoren is een vector die loodrecht staat op het vlak van die twee vectoren.quote:
Hoi ik zit met een vraag over wat vectoren. Het is volgens mij geen moeilijk probleem alleen zie ik het niet
Ik heb een punt N(x,y,z) en een punt M(x,y,z).
[snip]
quote:
Hoe ziet, bij ANOVA (A1-A2 en B1-B2, een tabel en/of grafiek eruit met:
a) een interactie effect van A, maar geen hoofd-effect van B
b) een interactie effect, hoofd-effect van A, maar geen hoofd-effect van B
c) een interactie effect, maar geen hoofd-effect
(of zijn vraag a en b eigenlijk hetzelfde?)
Herb is the healing of a nation, alcohol is the destruction.
Je moet eigenlijk iets duidelijker zijn over het punt O. Aan welke eisen moet het punt voldoen? En mag je er bijvoorbeeld van uit gaan dat de vector en MN loodrecht op elkaar staan (dat zou je uit het plaatje kunnen opmaken)? Maar je zoekt dus een vector die een een rechte hoek (90 graden) maakt met twee vectoren, als ik het goed begrijp.quote:
Hoi ik zit met een vraag over wat vectoren. Het is volgens mij geen moeilijk probleem alleen zie ik het niet
Ik heb een punt N(x,y,z) en een punt M(x,y,z). De genormaliseerde vector is een vector met lengte 1 (x,y,z). In dit plaatje dus (0,0,1).
Punt M-N levert een nieuwe vector op. Laten we deze a noemen.
Nu wil ik met deze informatie het punt O(x,y,z) bereken.
Als O-N een vector b is. Hoe reken ik dan dit punt uit? Hij moet dus gespiegeld worden over de genormaliseerde vector.
Hoop dat m'n vraag een beetje duidelijk is
[ afbeelding ]
Je zou dit als ik het goed heb op twee manieren kunnen doen. Riparius impliceert een bepaalde manier, maar het zou volgens mij ook zoals jij zei met een rotatiematrix (en dan wel eentje die om een bepaalde as roteert) kunnen. Dit is echter veel meer werk, dus echt aan te raden is het niet. Als het goed is komen beide manieren op hetzelfde uit (al zijn er twee mogelijkheden, 90 graden met de klok mee of 90 graden tegen de klok in).
Dus gebruik Riparius' post maar. OK een beetje nutteloze post dit, maargoed ik verveel me.
Finally, someone let me out of my cage
Hallo ik heb denk ik een heel simpel vraagje.
Ik ben bezig met een hoofdstuk over berg en dal parabolen.
Dat met dal parabolen snap ik maar met bergparabolen heb ik 1 probleem. Ik zal de vraag kopiëren om uit te het uit te leggen.
f(x) = -x2+4x
daar moest ik dus de tabel bij invullen.
Dat heb ik gedaan maar nu stuit ik op iets vreemds. Als ik het min kwadraat tussen haakjes zet (wat voor zover ik weet altijd moet) krijg ik een verkeerd antwoord, en als ik gewoon zonder haakjes invul goed.
voorbeeld : -22+4*2=4 en (-2)2+4*2=12
in de antwoorden staat dat bij x=2 f(x)=4 zou moeten zijn.
wie o wie weet wat ik fout doe of waarom er geen haakjes om het - kwadraat moeten?
alvast bedankt
Ik ben bezig met een hoofdstuk over berg en dal parabolen.
Dat met dal parabolen snap ik maar met bergparabolen heb ik 1 probleem. Ik zal de vraag kopiëren om uit te het uit te leggen.
f(x) = -x2+4x
daar moest ik dus de tabel bij invullen.
Dat heb ik gedaan maar nu stuit ik op iets vreemds. Als ik het min kwadraat tussen haakjes zet (wat voor zover ik weet altijd moet) krijg ik een verkeerd antwoord, en als ik gewoon zonder haakjes invul goed.
voorbeeld : -22+4*2=4 en (-2)2+4*2=12
in de antwoorden staat dat bij x=2 f(x)=4 zou moeten zijn.
wie o wie weet wat ik fout doe of waarom er geen haakjes om het - kwadraat moeten?
alvast bedankt
meestal moet dat gewoon hoor... wat is dan volgens het antwoordmodel de uitkomst van x=4?quote:
Hallo ik heb denk ik een heel simpel vraagje.
Ik ben bezig met een hoofdstuk over berg en dal parabolen.
Dat met dal parabolen snap ik maar met bergparabolen heb ik 1 probleem. Ik zal de vraag kopiëren om uit te het uit te leggen.
f(x) = -x2+4x
daar moest ik dus de tabel bij invullen.
Dat heb ik gedaan maar nu stuit ik op iets vreemds. Als ik het min kwadraat tussen haakjes zet (wat voor zover ik weet altijd moet) krijg ik een verkeerd antwoord, en als ik gewoon zonder haakjes invul goed.
voorbeeld : -22+4*2=4 en (-2)2+4*2=12
in de antwoorden staat dat bij x=2 f(x)=4 zou moeten zijn.
wie o wie weet wat ik fout doe of waarom er geen haakjes om het - kwadraat moeten?
alvast bedankt
daar zou 32 uit moeten komen lijkt me..
Herb is the healing of a nation, alcohol is the destruction.
Als er staat f(x) = -x², dan heb je f(2) = - 2² = - 4. Je berekent x² en zet er een minteken voor (want je moet eerst vermenigvuldigen en dan aftrekken... in dit geval dus aftrekken van 0 in feite). De tweede mogelijkheid is f(x) = (-x)² = (-x)(-x) = x * x = x². Dan heb je dus f(2) = 2² = 4.quote:
Hallo ik heb denk ik een heel simpel vraagje.
Ik ben bezig met een hoofdstuk over berg en dal parabolen.
Dat met dal parabolen snap ik maar met bergparabolen heb ik 1 probleem. Ik zal de vraag kopiëren om uit te het uit te leggen.
f(x) = -x2+4x
daar moest ik dus de tabel bij invullen.
Dat heb ik gedaan maar nu stuit ik op iets vreemds. Als ik het min kwadraat tussen haakjes zet (wat voor zover ik weet altijd moet) krijg ik een verkeerd antwoord, en als ik gewoon zonder haakjes invul goed.
voorbeeld : -22+4*2=4 en (-2)2+4*2=12
in de antwoorden staat dat bij x=2 f(x)=4 zou moeten zijn.
wie o wie weet wat ik fout doe of waarom er geen haakjes om het - kwadraat moeten?
alvast bedankt
Voor de duidelijkheid: er hoeven geen haakjes om omdat die er in de originele functie ook niet stonden.
Natuurlijk niet, het antwoordmodel klopt. f(4)= -4² + 4*4 = 0.quote:
[..]
meestal moet dat gewoon hoor... wat is dan volgens het antwoordmodel de uitkomst van x=4?
daar zou 32 uit moeten komen lijkt me..
ja x=-1 word -5quote:
[..]
meestal moet dat gewoon hoor... wat is dan volgens het antwoordmodel de uitkomst van x=4?
daar zou 32 uit moeten komen lijkt me..
x=1 word 3
x=2 word 4
x=3 word 3
x=4 word 0
Foutje van het boek dan?
Kan het ook niet controleren want staat maar 1 vraag in over bergparabolen de rest gaat over dalparabolen.
overigens denk ik dat jij in plaats van plus een keer heb ingetypt bij de 4
oh oke dat is dus de trick eerst vermenigvuldigenquote:
[..]
Als er staat f(x) = -x², dan heb je f(2) = - 2² = - 4. Je berekent x² en zet er een minteken voor (want je moet eerst vermenigvuldigen en dan aftrekken... in dit geval dus aftrekken van 0 in feite). De tweede mogelijkheid is f(x) = (-x)² = (-x)(-x) = x * x = x². Dan heb je dus f(2) = 2² = 4.
bedankt voor de hulp
Inderdaad moet je eerst vermenigvuldigen, maar hier vermenigvuldig je niet - hier verhef je een macht (machtsverhef je?)! Dat heeft een nog hogere prioriteit.quote:
want je moet eerst vermenigvuldigen en dan aftrekken... in dit geval dus aftrekken van 0 in feite.
Wat betreft haakjes om negatieve getallen: alleen doen als je een negatief getal invult voor x. Hier stond de min al gewoon in de formule, dus moet je de hele x2 als een negatief getal zien (en dus niet alleen x).
Je hebt gelijk. Maar machtsverheffen kan je zien als vermenigvuldigen en dan staat er gewoon -x*x. Als je -2x² hebt betekent dit natuurlijk niet (-2x)² maar -2(x²).quote:
[..]
Inderdaad moet je eerst vermenigvuldigen, maar hier vermenigvuldig je niet - hier verhef je een macht (machtsverhef je?)! Dat heeft een nog hogere prioriteit.
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |