SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Kijk hier eens. Dat had je zelf toch ook kunnen vinden?quote:Op woensdag 22 juni 2011 12:35 schreef M.rak het volgende:
Ik kom niet uit de volgende opgave:
[ afbeelding ]
Ik ken de formules voor de normaalvector en het raakvlak in twee dimensies, maar nu is F ook nog een functie van z. Ik zou zeggen dat je nu iets met impliciete functies moet doen, maar ik zou niet weten hoe je dat hier toe moet passen.
Variabelen scheiden en dan beide leden integreren.quote:
[ afbeelding ]
Even klein vraagje, hoe integreer je deze ook alweer naar een exponentiële functie in de vorm van
[ afbeelding ]
Je hebt gelijk, daar heb ik helemaal niet aan gedacht. Bedanktquote:
[..]
Kijk hier eens. Dat had je zelf toch ook kunnen vinden?
.Ik heb direct nog een vraag. In een tentamen stond een opgave waarin oa het volgende werd gevraagd:
Bepaal de snijpunten van het vlak (x-1)2 + (y-2)2 + (z-3)2 = 1 en de lijn x = y = z.
Bij alles wat ik probeer zijn er geen oplossingen, maar in de uitwerkingen staat dat (1,1,1) en (3,3,3) de oplossingen zijn. Ben ik nu heel dom en zie ik iets over het hoofd, of is dit gewoon een fout in de tentamenuitwerkingen en zijn er geen oplossingen?
The biggest argument against democracy is a five minute discussion with the average voter.
Het vlak is een bol met middelpunt (1;2;3) en straal 1. De afstand van de punten (1;1;1) en (3;3;3) tot het middelpunt (1;2;3) bedraagt echter √5 en deze punten liggen dus buiten de bol, zodat je meteen ziet dat de uitwerking niet klopt. De lijn x=y=z ligt geheel buiten de bol.quote:
[..]
Je hebt gelijk, daar heb ik helemaal niet aan gedacht. Bedankt
Ik heb direct nog een vraag. In een tentamen stond een opgave waarin oa het volgende werd gevraagd:
Bepaal de snijpunten van het vlak (x-1)2 + (y-2)2 + (z-3)2 = 1 en de lijn x = y = z.
Bij alles wat ik probeer zijn er geen oplossingen, maar in de uitwerkingen staat dat (1,1,1) en (3,3,3) de oplossingen zijn. Ben ik nu heel dom en zie ik iets over het hoofd, of is dit gewoon een fout in de tentamenuitwerkingen en zijn er geen oplossingen?
Bedankt alweer 
. Nog één vraag, dan hou ik er mee op:
In de uitwerkingen staat dat deze limiet niet bestaat, omdat er verschillende antwoorden uitkomen bij het pad y=x en het pad x=0. Als je y=x invult komt er ½ uit, maar als je x=0 invult komt er volgens de uitwerkingen nul uit. De teller wordt dan inderdaad nul, maar volgens mij wordt de noemer ook nul, waardoor je 0/0 overhoudt. Daar kan je niets over zeggen, dus heb je toch niks aan dat pad? Ik kon ook geen ander pad verzinnen waar direct aan te zien is dat de limiet niet bestaat.
. Nog één vraag, dan hou ik er mee op:
In de uitwerkingen staat dat deze limiet niet bestaat, omdat er verschillende antwoorden uitkomen bij het pad y=x en het pad x=0. Als je y=x invult komt er ½ uit, maar als je x=0 invult komt er volgens de uitwerkingen nul uit. De teller wordt dan inderdaad nul, maar volgens mij wordt de noemer ook nul, waardoor je 0/0 overhoudt. Daar kan je niets over zeggen, dus heb je toch niks aan dat pad? Ik kon ook geen ander pad verzinnen waar direct aan te zien is dat de limiet niet bestaat.
The biggest argument against democracy is a five minute discussion with the average voter.
Werk de tellers en noemers niet apart uit, maar vereenvoudig eerst.
Bij een limiet is de waarde in het punt (0,0) niet van belang, dus 0 invullen doe je alleen bij continue functies. Deze functie is niet continu in (0,0).
Bij een limiet is de waarde in het punt (0,0) niet van belang, dus 0 invullen doe je alleen bij continue functies. Deze functie is niet continu in (0,0).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik zie het, als je zowel de teller als de noemer vermenigvuldigt met sqrt(x) kan je x wegdelen, dan lukt het wel.
The biggest argument against democracy is a five minute discussion with the average voter.
Dat hoeft niet, er staat gewoon a/(a+a) en dat is 1/2.quote:Op woensdag 22 juni 2011 19:18 schreef M.rak het volgende:
Ik zie het, als je zowel de teller als de noemer vermenigvuldigt met sqrt(x) kan je x wegdelen, dan lukt het wel.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Waarom zou je geen ander pad kunnen verzinnen? Elke lijn door de oorsprong voldoet. Kies je (om maar een voorbeeld te geven) y = ¼x dan kom je op 4/3 uit en dat is in combinatie met de waarde 1/2 voor y = x voldoende om te concluderen dat de limiet niet bestaat.quote:
Bedankt alweer
[ afbeelding ]
In de uitwerkingen staat dat deze limiet niet bestaat, omdat er verschillende antwoorden uitkomen bij het pad y=x en het pad x=0. Als je y=x invult komt er ½ uit, maar als je x=0 invult komt er volgens de uitwerkingen nul uit. De teller wordt dan inderdaad nul, maar volgens mij wordt de noemer ook nul, waardoor je 0/0 overhoudt. Daar kan je niets over zeggen, dus heb je toch niks aan dat pad? Ik kon ook geen ander pad verzinnen waar direct aan te zien is dat de limiet niet bestaat.
Iemand een idee? 't lukt mezelf niet om een simpel goed voorbeeld te verzinnen met getallen.
Zelf had ik 't volgende verzonnen;
A = nulverzameling.
B = {True, False}
C = {True, False}
F(x) = x
G1(x) = (x & True)
G2(x) = not (x || True)
dan
x in A = False
G1(F(x)) = False = G2(F(x))
maar
y in B = True of False, voor True geldt dan
G1(True) = True != False = G2(True)
opzich klopt het wel maar niet echt een 'overtuigend' voorbeeld imo
Weet je het zeker?quote:
[..]
Dat hoeft niet, er staat gewoon a/(a+a) en dat is 1/2.
ah ik zit verkeerd te lezen, voor x=y is het duidelijk, maar x=0 werkt natuurlijk niet.quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hoe haal ik uit een cijfer het aantal uren, minuten en secondes?
dus 3600 = 1 uur 0 minuten en 0 secondes
maar hoe moet dat met een getal als 10000000
wat is de berekening ??
dus 3600 = 1 uur 0 minuten en 0 secondes
maar hoe moet dat met een getal als 10000000
wat is de berekening ??
Je kan niet een getal zonder eenheid omrekenen naar een getal met een eenheid.
Ik ga er vanuit dat je bedoelt hoe je van het aantal secondes kan naar aantal "uur, minuten, secondes".
Als je 10000000 seconde hebt, dan zijn dat in totaal 10000000/60 minuten, of 10000000/(60*60) uur. Dat is 166666,666... uur. Dat zijn dus 166666 hele uren, plus nog 0,666... = 2/3 uur. 2/3 uur = 40min. Dus 10000000 sec = 166666 uur en 40 min (en 0sec).
Ik ga er vanuit dat je bedoelt hoe je van het aantal secondes kan naar aantal "uur, minuten, secondes".
Als je 10000000 seconde hebt, dan zijn dat in totaal 10000000/60 minuten, of 10000000/(60*60) uur. Dat is 166666,666... uur. Dat zijn dus 166666 hele uren, plus nog 0,666... = 2/3 uur. 2/3 uur = 40min. Dus 10000000 sec = 166666 uur en 40 min (en 0sec).
Weet iemand hoe je webgrafieken tekent in Mathematica?
Of wat de Engelse term is voor webgrafiek? Met "web diagram" kom ik niet veel verder.
Of wat de Engelse term is voor webgrafiek? Met "web diagram" kom ik niet veel verder.
Je kunt om te beginnen hier: http://reference.wolfram.com/mathematica/ref/RecurrenceTable.html even kijken. Ik weet niet of het type grafiek dat jij zoekt een ingebouwde mogelijkheid is, maar indien niet is het niet al te moeilijk hem zelf eventjes te schrijven lijkt me?quote:
Weet iemand hoe je webgrafieken tekent in Mathematica?
Of wat de Engelse term is voor webgrafiek? Met "web diagram" kom ik niet veel verder.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Je voorbeeld klopt, een ander voorbeeld kun je maken met A={1}, B={1,2}, en F(x)=x.quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Het is een ingebouwde functie, heb het wel eens eerder gebruikt maar ik kan het niet terugvinden. Ook niet met de termen cobweb plot of verhulst diagram...quote:
[..]
Je kunt om te beginnen hier: http://reference.wolfram.com/mathematica/ref/RecurrenceTable.html even kijken. Ik weet niet of het type grafiek dat jij zoekt een ingebouwde mogelijkheid is, maar indien niet is het niet al te moeilijk hem zelf eventjes te schrijven lijkt me?
Ik weet het alweer, had toch een standaard code van een ander gebruikt (en t is dus geen ingebouwde functie).
[ Bericht 11% gewijzigd door thenxero op 25-06-2011 15:23:55 ]
S is het lichaam in R3 gegeven door
S= {(x,y,z) zitten in R3 | x,z >= 0 , x^2+y^2 <= 1, y + z <= 1}
Bereken volume.
Kan iemand me hierbij helpen? Is de bedoeling om het niet in cylindrische coordinaten te doen, maar waarschijnlijk d.m.v. changes of variables (jacobian?) alvast bedankt!
S= {(x,y,z) zitten in R3 | x,z >= 0 , x^2+y^2 <= 1, y + z <= 1}
Bereken volume.
Kan iemand me hierbij helpen? Is de bedoeling om het niet in cylindrische coordinaten te doen, maar waarschijnlijk d.m.v. changes of variables (jacobian?) alvast bedankt!
Kan dit niet met een of twee dubbelintegralen, waarbij je integreert over het vlak x/y?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Kan het niet ook gewoon door middel van inspectie?
The biggest argument against democracy is a five minute discussion with the average voter.
Met (x,y,z) = (1,0,1) in de halve bol?quote:
Volgens mij is dat een halve bol met straal 1.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Toch niet inderdaad, en ook nog x>=0 dus cirkel als basis gaat ook niet op.quote:Op zaterdag 25 juni 2011 16:51 schreef GlowMouse het volgende:
[..]
Met (x,y,z) = (1,0,1) in de halve bol?
edit:
Een halve kegel dan.
Beneath the gold, bitter steel
Volgens mij is het een deel van de cilinder met straal 1, hoogte 2 en als middelpunt de oorsprong. Door alleen het deel te pakken waarvoor geldt x >= 0 (dan hou je de helft van het volume over) en daarvan weer alleen het deel te pakken wat onder het vlak y+z=1 ligt (dan hou je weer de helft over) krijg je het gewenste volume.
Het volume is dan volgens mij dus pi/2.
Het volume is dan volgens mij dus pi/2.
The biggest argument against democracy is a five minute discussion with the average voter.
Antwoord klopt inderdaad maar kan iemand me voordoen hoe het met een mooie integraal uit te rekenen is
Dat is toch niet zo moeilijk? Kijk hier eens.quote:
Antwoord klopt inderdaad maar kan iemand me voordoen hoe het met een mooie integraal uit te rekenen is
P(beide wielen 10)= 1/10*1/10=1/100 op 5 euroquote:In een speelautomaat draaien twee onafhankelijke raden die in tien gelijke segmenten zijn verdeeld. De segmenten zijn van 1 tm 10 genummerd. Er gelden de volgende winst mogelijkheden (bij andere combinaties verliest de speler zijn inzet):
-Beide raden 10 = 5 euro
-Beide raden hetzelfde getal (maar niet 10) = 2 euro
-Precies één van de raden een 10 = 1 euro
Wat is de minimale inzet die je moet vragen om winst te maken?
P(beide wielen zelfde maar niet 10)= 10/100-1/100= 9/100 op 2 euro
P(precies één 10)= 1/10*9/10=9/100 op 1 euro
(5*1/100)+(2*9/100)+(1*9/100)=5/100+18/100+9/100=32/100
Gemiddeld 0.32 euro per spel winst,dus moet je minimaal 0.33 euro inzet vragen
Maar ik heb het idee dat ik het veel te makkelijk aanpak en ergens goed verkeerd zit.
Ik zou zeggen dat de methode klopt, alleen P(precies één 10) is volgens mij 18/100, allebei de raden kunnen namelijk die 10 krijgen.
The biggest argument against democracy is a five minute discussion with the average voter.
Wat M.rak zegt. En eigenlijk is die vraag slecht gesteld: met 1ct inzet kan al winst gemaakt worden, alleen de verwachte opbrengst voor de ondernemer is dan negatief.
Ok bedankt, vreemd ik had echt iets veel moeilijkers verwacht.quote:
Ik zou zeggen dat de methode klopt, alleen P(precies één 10) is volgens mij 18/100, allebei de raden kunnen namelijk die 10 krijgen.
Ja ik heb de vraag niet letterlijk overgetyptquote:
Wat M.rak zegt. En eigenlijk is die vraag slecht gesteld: met 1ct inzet kan al winst gemaakt worden, alleen de verwachte opbrengst voor de ondernemer is dan negatief.
Korte vraag.
Ik was ergens als deelprobleempje aan het uitrekenen hoeveel verschillende blokken van grootte k er zijn die geen van de punten van een bepaalde verzameling J, met |J|=bevatten. Totaal zijn er v punten.
Daarvoor kreeg ik ergens de uitdrukking v-j boven k (namelijk v-j toegestane punten, waar je er k uit kan kiezen. )
Ik had hier echter (blijkt) v-k boven j moeten gebruiken (v-k zijn de punten niet in je blok en daar moeten de j punten in liggen).
In het algemeen zijn deze uitdrukkingen niet gelijk, dus waarom moet ik de tweede uitdrukking gebruiken en niet de eerste? Waar ligt dat verschil?
(Dit is uit Design theorie, maar dit specifieke probleem is gewoon elementaire combinatoriek).
Ik was ergens als deelprobleempje aan het uitrekenen hoeveel verschillende blokken van grootte k er zijn die geen van de punten van een bepaalde verzameling J, met |J|=bevatten. Totaal zijn er v punten.
Daarvoor kreeg ik ergens de uitdrukking v-j boven k (namelijk v-j toegestane punten, waar je er k uit kan kiezen. )
Ik had hier echter (blijkt) v-k boven j moeten gebruiken (v-k zijn de punten niet in je blok en daar moeten de j punten in liggen).
In het algemeen zijn deze uitdrukkingen niet gelijk, dus waarom moet ik de tweede uitdrukking gebruiken en niet de eerste? Waar ligt dat verschil?
(Dit is uit Design theorie, maar dit specifieke probleem is gewoon elementaire combinatoriek).
Pak bv. V={1,2,3,4}, J={1}, k=2.
v-j boven k is 3.
v-k boven j is 2.
Het juiste antwoord is v-j boven k:
{2,3}
{2,4}
{3,4}
v-j boven k is 3.
v-k boven j is 2.
Het juiste antwoord is v-j boven k:
{2,3}
{2,4}
{3,4}
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dat dacht ik dus ook... zal anders even de gehele context erbij doen?quote:
Pak bv. V={1,2,3,4}, J={1}, k=2.
v-j boven k is 3.
v-k boven j is 2.
Het juiste antwoord is v-j boven k:
{2,3}
{2,4}
{3,4}
Het gaat om die schets van het bewijs bij 19.4. De rest zit er bij om de context/notatie te verduidelijken....
Hallo,
heb morgen een wiskunde toets en zou graag antwoord willen op deze vraag:
Heb 2.5Q^-0.5 + 2
Uiteindelijk moet ik dit verder herleiden tot (5:2)x(1:Q^1:2) + 2
Hoe doe ik dit?
heb morgen een wiskunde toets en zou graag antwoord willen op deze vraag:
Heb 2.5Q^-0.5 + 2
Uiteindelijk moet ik dit verder herleiden tot (5:2)x(1:Q^1:2) + 2
Hoe doe ik dit?
2.5 = 5/2quote:
Hallo,
heb morgen een wiskunde toets en zou graag antwoord willen op deze vraag:
Heb 2.5Q^-0.5 + 2
Uiteindelijk moet ik dit verder herleiden tot (5:2)x(1:Q^1:2) + 2
Hoe doe ik dit?
Q-0.5 = 1/Q0.5 = 1/√Q
Met deze info moet dat wel lukken toch
Niet altijd serieus
Ik heb een vraag over exponentiële groei.
De formule is het volgende:
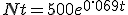
De vraag luidt: Wat is t als N=2400.
oftewel:
2400 =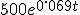
Hoe bereken je dit?
De formule is het volgende:
De vraag luidt: Wat is t als N=2400.
oftewel:
2400 =
Hoe bereken je dit?
Of niet?
beide kanten delen door 500, dan de LN van beide kanten nemen!quote:
Ik heb een vraag over exponentiële groei.
De formule is het volgende:
[ afbeelding ]
De vraag luidt: Wat is t als N=2400.
oftewel:
2400 = [ afbeelding ]
Hoe bereken je dit?
Volg je dat?
~Si vis amari, ama~
Als N = 2400, dan staat er links wel 2400t, behoorlijk verschilquote:
Ik heb een vraag over exponentiële groei.
De formule is het volgende:
[ afbeelding ]
De vraag luidt: Wat is t als N=2400.
oftewel:
2400 = [ afbeelding ]
Hoe bereken je dit?
Edit: neem aan 0.069t, maar lijkt zo op 0*0.069t
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
Ik verwacht dat hij bedoelt N(t) en niet N*t, anders wordt het inderdaad een stukje lastiger.quote:
[..]
Als N = 2400, dan staat er links wel 2400t, behoorlijk verschil
Edit: neem aan 0.069t, maar lijkt zo op 0*0.069t
The biggest argument against democracy is a five minute discussion with the average voter.
Klinkt bekent, maar volgen doe ik je niet..quote:
[..]
beide kanten delen door 500, dan de LN van beide kanten nemen!
Volg je dat?
quote:
[..]
Ik verwacht dat hij bedoelt N(t) en niet N*t,
Of niet?
Het delen lukt denk ik wel? Als je dan aan beide kanten de ln (de natuurlijke logaritme) neemt, komt er links ln(4.8) te staan, en recht ln(exp(0.069t)). Een eigenschap van ln(x) en exp(x) (dat is e^x) is dat ze elkaar opheffen, dus ln(exp(0.069t))=0.069t. Nu staat er ln(4.8)=0.069t, dat levert t = ln(4.8)/0.069.quote:
[..]
Klinkt bekent, maar volgen doe ik je niet..
Zo duidelijker?
The biggest argument against democracy is a five minute discussion with the average voter.
dacht laat het hem zelf proberen, maar dat lukt schijnbaar toch nietquote:
[..]
Het delen lukt denk ik wel? Als je dan aan beide kanten de ln (de natuurlijke logaritme) neemt, komt er links ln(4.8) te staan, en recht ln(exp(0.069t)). Een eigenschap van ln(x) en exp(x) (dat is e^x) is dat ze elkaar opheffen, dus ln(exp(0.069t))=0.069t. Nu staat er ln(4.8)=0.069t, dat levert t = ln(4.8)/0.069.
Zo duidelijker?
Wat voor niveau doe je, Self-Catering?
~Si vis amari, ama~
LBO Zwakstroomquote:
[..]
dacht laat het hem zelf proberen, maar dat lukt schijnbaar toch niet
Wat voor niveau doe je, Self-Catering?
Nee, zit met het (zelfstudie)boek van Jan Craats, daar wordt expo groei echt zwaar onderbelicht.
Of niet?
Wat themole zegt inderdaad (behalve dan a2 ipv 2a2). Je kan het ook zelf uitwerken, (a+b)2 is namelijk gewoon (a+b)(a+b). Dat is weer gelijk aan a(a+b) + b(a+b). Uitwerken levert op a2+2ab+b2, en dat is wat themole al zei.
The biggest argument against democracy is a five minute discussion with the average voter.
Oeps onhandige typo.quote:
Wat themole zegt inderdaad (behalve dan a2 ipv 2a2). Je kan het ook zelf uitwerken, (a+b)2 is namelijk gewoon (a+b)(a+b). Dat is weer gelijk aan a(a+b) + b(a+b). Uitwerken levert op a2+2ab+b2, en dat is wat themole al zei.
Niet altijd serieus
Laatste vraag voor nu:
De afgeleide van
0.5t^4 - a^2 t + a^2
t zit meteen achter de 2 vast
2t^3 - a^2
Hoe kan dat?
En waarom veranderd -3pa in -3p volgens de afgeleide regel?
Bedankt voor de komende uitleg!!!
De afgeleide van
0.5t^4 - a^2 t + a^2
t zit meteen achter de 2 vast
2t^3 - a^2
Hoe kan dat?
En waarom veranderd -3pa in -3p volgens de afgeleide regel?
Bedankt voor de komende uitleg!!!
f(x)=bxn+cx+d
f'(x)=n*bxn-1+c
Die p in -3pa is als het ware getal terwijl dat a het variabele deel is. Dan is de afgeleide van -3pa, -3p. Als je differentieert naar p wordt wordt de afgeleide van -3pa, -3a. Het is maar net of je de a of p als getal laat fungeren. Maar staat er geen betere uitleg in je boek?
f'(x)=n*bxn-1+c
Die p in -3pa is als het ware getal terwijl dat a het variabele deel is. Dan is de afgeleide van -3pa, -3p. Als je differentieert naar p wordt wordt de afgeleide van -3pa, -3a. Het is maar net of je de a of p als getal laat fungeren. Maar staat er geen betere uitleg in je boek?
Niet altijd serieus
Nee helaas worden over die dingen geen uitleg gegeven. Ik zou toch zeggen dat de eerste formule,
0.5t^4 - a^2 t + a^2
t zit meteen achter de 2 vast
2t^3 - a^2 + a^2 als uitkomst zou moeten hebben? Je werkt de t achter a^2 weg en differentieerd de a^2 naar a^2?
0.5t^4 - a^2 t + a^2
t zit meteen achter de 2 vast
2t^3 - a^2 + a^2 als uitkomst zou moeten hebben? Je werkt de t achter a^2 weg en differentieerd de a^2 naar a^2?
Je vergeet het principe dat f(x)=a dan f'(x)=0quote:
Nee helaas worden over die dingen geen uitleg gegeven. Ik zou toch zeggen dat de eerste formule,
0.5t^4 - a^2 t + a^2
t zit meteen achter de 2 vast
2t^3 - a^2 + a^2 als uitkomst zou moeten hebben? Je werkt de t achter a^2 weg en differentieerd de a^2 naar a^2?
Dus die laatste a^2 valt weg.
Niet altijd serieus
Jouw formule is:quote:
Huh, sorry, maar dat snap ik niet? Zou je dat kunnen uitleggen?
f(t)=0.5t4- a2t + a2
f1(t)=0.5t4 -> f'1(t)=2t3
f2(t)=- a2t -> f'2(t)=-a2
f3(t)=- a2 -> f'3(t)=-0
f'(x)= f'1(t)+f'2(t)+f'3(t)=2t3-a2
a^2 is in dit geval gewoon niks meer niks minder dan een parameter, voor die a^2 had ook 10 of 1000 kunnen staan. Dus de afgeleide is 0.
Niet altijd serieus
Ik vind het nog steeds heel moeilijk te begrijpen. Sorry, het ligt aan mij. Maar is dit dus een speciale uitzondering? Want naar mijn gevoel zou a^2 altijd naar 2a herleid moeten worden?
Je differentieert altijd naar een variabele. Als jij zegt dat f(t)=0.5t4- a2t + a2, dan kijk je naar een functie van t. Als je dan gaat differentieren, differentieer je naar de variabele t, en niet naar a. In dit geval is a gewoon een plaatsvervanger voor een getal, zodat je later a=10 of a=20 in kan vullen, zonder dat je alles weer opnieuw moet uitrekenen.quote:
Ik vind het nog steeds heel moeilijk te begrijpen. Sorry, het ligt aan mij. Maar is dit dus een speciale uitzondering? Want naar mijn gevoel zou a^2 altijd naar 2a herleid moeten worden?
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!
Je differentieert naar t, dus t is een variabele. Als p een getal is kan je pt toch herleiden naar p. Dan kan je p2t herleiden naar p2. Je weet dat de afgeleide van 9 gelijk is aan 0. p is een getal dus de afgeleide van p2 als je diffentieert naar t dan is dat 0. Indien je differentieert naar p dan is p ipv een constante een variabele en is de afgeleide van p2 ineens 2p.quote:
Ik vind het nog steeds heel moeilijk te begrijpen. Sorry, het ligt aan mij. Maar is dit dus een speciale uitzondering? Want naar mijn gevoel zou a^2 altijd naar 2a herleid moeten worden?
Maar heb je de stof eerder bestudeert, dan zou je dit namelijk toch zijn tegengekomen en had je het misschien aan een leraar kunnen vragen. (Hetgeen ik absoluut niet ben.)
Niet altijd serieus
Ik zie niet in waarom de lijn l (als functie van de hoek a) die door de oorsprong gaat en een hoek a met de oorsprong maakt, weergegeven kan worden door de vergelijking:
-xsin(a) + ycos(a)=0
-xsin(a) + ycos(a)=0
De richtingscoëfficiënt van een rechte lijn is gelijk aan de tangens van de hoek die de lijn met de (positieve) x-as maakt, begrijp je dat wel?quote:
Ik zie niet in waarom de lijn l (als functie van de hoek a) die door de oorsprong gaat en een hoek a met de oorsprong maakt, weergegeven kan worden door de vergelijking:
-xsin(a) + ycos(a)=0
Ja, maar ik zie even niet wat ik daarmee kan.quote:
[..]
De richtingscoëfficiënt van een rechte lijn is gelijk aan de tangens van de hoek die de lijn met de (positieve) x-as maakt, begrijp je dat wel?
Laten we aannemen dat we een lijn door de oorsprong hebben die een (positieve) hoek α maakt met de (positieve) x-as. Kies nu een willekeurig punt P(x;y) op de lijn in het eerste kwadrant. Zij Q(x;0) het voetpunt van de loodlijn uit P op de x-as en beschouw nu driehoek OPQ met hoek QOP = α. De tangens van een (scherpe) hoek in een rechthoekige driehoek is gelijk aan de lengte van overliggende rechthoekszijde gedeeld door de lengte van de aanliggende rechthoekszijde, en deze lengten zijn hier resp. y en x. Dus krijgen we:quote:
[..]
Ja, maar ik zie even niet wat ik daarmee kan.
(1) y : x = tan α
Maar nu is ook:
(2) tan α = sin α : cos α
En dus hebben we:
(3) y : x = sin α : cos α
Kruislings vermenigvuldigen van de leden van deze evenredigheid geeft dan:
(4) y∙cos α = x∙sin α
Analoog voor lijnen door de oorsprong met een negatieve richtingscoëfficiënt.
Ik snap werkelijk niet waarom ik dit niet zelf zag.quote:
[..]
Laten we aannemen dat we een lijn door de oorsprong hebben die een (positieve) hoek α maakt met de (positieve) x-as. Kies nu een willekeurig punt P(x;y) op de lijn in het eerste kwadrant. Zij Q(x;0) het voetpunt van de loodlijn uit P op de x-as en beschouw nu driehoek OPQ met hoek QOP = α. De tangens van een (scherpe) hoek in een rechthoekige driehoek is gelijk aan de lengte van overliggende rechthoekszijde gedeeld door de lengte van de aanliggende rechthoekszijde, en deze lengten zijn hier resp. y en x. Dus krijgen we:
(1) y : x = tan α
Maar nu is ook:
(2) tan α = sin α : cos α
En dus hebben we:
(3) y : x = sin α : cos α
Kruislings vermenigvuldigen van de leden van deze evenredigheid geeft dan:
(4) y∙cos α = x∙sin α
Analoog voor lijnen door de oorsprong met een negatieve richtingscoëfficiënt.
Bedankt voor de uitleg.
Het zal de hitte wel zijn. Misschien is het aardig om te laten zien dat je hetzelfde resultaat ook op een heel andere manier kunt vinden. Zij l weer de lijn die je krijgt door de x-as over een (positieve of negatieve) hoek α te roteren om de oorsprong. Beschouw nu de vector:quote:
[..]
Ik snap werkelijk niet waarom ik dit niet zelf zag.
Bedankt voor de uitleg.
(1) n = (cos(α+½π) sin(α+½π))
Het is duidelijk dat n loodrecht staat op lijn l en dus een normaalvector is van l. Voor elke vector v = (x y) met eindpunt op lijn l is het inproduct van n en v dus gelijk aan nul:
(2) v∙n = 0
En dus hebben we voor elk punt (x;y) op lijn l:
(3) x∙cos(α+½π) + y∙sin(α+½π) = 0
Maar nu is cos(α+½π) = -sin α en sin(α+½π) = cos α, en dus hebben we als vergelijking voor l:
(4) -x∙sin α + y∙cos α = 0
In tegenstelling tot de vorige afleiding geldt deze afleiding ook voor α = ½π.
En G(x) dan?quote:
[..]
Je voorbeeld klopt, een ander voorbeeld kun je maken met A={1}, B={1,2}, en F(x)=x.
G1 en G2 moeten dezelfde functiewaarde hebben voor 1, en een andere voor 2.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dit is inderdaad een erg mooie en duidelijke afleiding.quote:
[..]
Het zal de hitte wel zijn. Misschien is het aardig om te laten zien dat je hetzelfde resultaat ook op een heel andere manier kunt vinden. Zij l weer de lijn die je krijgt door de x-as over een (positieve of negatieve) hoek α te roteren om de oorsprong. Beschouw nu de vector:
(1) n = (cos(α+½π) sin(α+½π))
Het is duidelijk dat n loodrecht staat op lijn l en dus een normaalvector is van l. Voor elke vector v = (x y) met eindpunt op lijn l is het inproduct van n en v dus gelijk aan nul:
(2) v∙n = 0
En dus hebben we voor elk punt (x;y) op lijn l:
(3) x∙cos(α+½π) + y∙sin(α+½π) = 0
Maar nu is cos(α+½π) = -sin α en sin(α+½π) = cos α, en dus hebben we als vergelijking voor l:
(4) -x∙sin α + y∙cos α = 0
In tegenstelling tot de vorige afleiding geldt deze afleiding ook voor α = ½π.
Wat ik erg jammer vind aan de opzet van mijn studie (wiskunde), is dat er totaal geen 'praktijk' meer is. Zoals bij lineaire algebra is de enige matrix die niet puur algemeen/theoretisch was ( 'laat M een nxn matrix zijn in het complexe vlak, dan...' ), de rotatiematrix geweest en dan nog diende die alleen om een verband tussen draaien/spiegelen en orthogonale transformaties te tonen.
Ik neem aan dat daarvoor de minor natuurkunde dient?
Oei, dat is in het tweede jaar nog vele malen "erger". Als je wat verder komt met natuurkunde is het ook niet heel veel anders... quantummechanica heeft ook niet zoveel met de dagelijkse praktijk te maken.quote:
[..]
Dit is inderdaad een erg mooie en duidelijke afleiding.
Wat ik erg jammer vind aan de opzet van mijn studie (wiskunde), is dat er totaal geen 'praktijk' meer is. Zoals bij lineaire algebra is de enige matrix die niet puur algemeen/theoretisch was ( 'laat M een nxn matrix zijn in het complexe vlak, dan...' ), de rotatiematrix geweest en dan nog diende die alleen om een verband tussen draaien/spiegelen en orthogonale transformaties te tonen.
Ik neem aan dat daarvoor de minor natuurkunde dient?
Maar bij natuurkunde (in ieder geval het eerste jaar) ben je tenminste nog bezig met concrete matrices. En dat bedoel ik met 'praktijk'.quote:Op donderdag 30 juni 2011 00:14 schreef thenxero het volgende:
[..]
Oei, dat is in het tweede jaar nog vele malen "erger". Als je wat verder komt met natuurkunde is het ook niet heel veel anders... quantummechanica heeft ook niet zoveel met de dagelijkse praktijk te maken.
Niet dat ik klaag, ik vind deze manier ook leuk.
Het is alleen frustrerend dat een paar uurtjes in een natuurkunde boek kijken me meer begrip heeft gebracht van vectoren dan een heel semester lineaire algebra 1.
Vraagje... Ik heb de relatie R op |N+. x en y zijn gerelateerd als er een k en l bestaan in |N+ zodat x^k = y^l. Nu moet ik bewijzen dat de relatie transitief is. Dus xRy & yRz implicieert xRz. Nu kom ik niet echt uit in de wiskunde.
x^k = y^l en y^m = z^n. Nu moet ik dus een p en q verzinnen zodat x^p = x^q. Nu is mijn vraag hoe kom ik aan de p en q? Ik zie niet echt in hoe ik vanuit hetgene gegeven de exponenten zodanig kan manipuleren dat ik de nieuwe p en q exponenten verkrijg die x en z met elkaar relateren.
x^k = y^l en y^m = z^n. Nu moet ik dus een p en q verzinnen zodat x^p = x^q. Nu is mijn vraag hoe kom ik aan de p en q? Ik zie niet echt in hoe ik vanuit hetgene gegeven de exponenten zodanig kan manipuleren dat ik de nieuwe p en q exponenten verkrijg die x en z met elkaar relateren.
ik zal een opzetje geven:
Je hebt xk = yi en ym = zn
er geldt dus dat
xk = yi = (ym)i/m
Je hebt xk = yi en ym = zn
er geldt dus dat
xk = yi = (ym)i/m
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
In dat natuurkundeboek staat alles waarschijnlijk een stuk minder exact uitgelegd dan in je wiskundeboek (dat is toch vaak wel het geval). Daardoor krijg je misschien bij natuurkunde een wat intuïtiever begrip, maar als je de theorie wil uitbreiden of op verschillende dingen wil toepassen, dan heb je vaak weer meer aan de "droge" wiskundige manier, die wat algemener en abstracter is.quote:
[..]
Maar bij natuurkunde (in ieder geval het eerste jaar) ben je tenminste nog bezig met concrete matrices. En dat bedoel ik met 'praktijk'.
Niet dat ik klaag, ik vind deze manier ook leuk.
Het is alleen frustrerend dat een paar uurtjes in een natuurkunde boek kijken me meer begrip heeft gebracht van vectoren dan een heel semester lineaire algebra 1.
Ik heb zelf 1 jaar natuurkunde gestudeerd, maar ben ermee gestopt omdat ik het wiskundig correcte verkoos boven het natuurkundige "da's intuïtief toch logisch" gepraat.
Duidelijkquote:
ik zal een opzetje geven:
Je hebt xk = yi en ym = zn
er geldt dus dat
xk = yi = (ym)i/m
xk = yi = (ym)i/m = (zn)i/m
Nu alleen dus nog bewijzen dat n*i/m in |N+ zit
Dat zal niet lukken, maar dat is niet erg.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hoe verder dan? Of dit antwoord gewoon laten staan...? Lijkt me sterkquote:Op donderdag 30 juni 2011 16:45 schreef GlowMouse het volgende:
Dat zal niet lukken, maar dat is niet erg.
Het lijkt mij inzichtelijker om meteen te gebruiken dat als een relatie aangetoond wordt door een paar exponenten a, b dat het paar m*a, m*b dit ook doet (ik vermoed dat GlowMouse dit uiteindelijk ook wel zal doen). Die m_xy en m_yz moet je dan zodanig kiezen dat de exponenten van y hetzelfde zijn.quote:
[..]
Hoe verder dan? Of dit antwoord gewoon laten staan...? Lijkt me sterk
kleine vraag. Ik moet
f(n) + g(n) = Θ(min(f(n), g(n))) bewijzen of ontkrachten
Bedoelen ze hier met min(f(n), g(n)) de functie van g(n) en f(n) die asymptotisch het kleinste is (oftewel het minst hard stijgt)?
Er staat geen verdere uitleg in het boek, althans niet waar ik het kan vinden (boek is meer dan 1800 pagina's). Ik weet btw niet echt of deze vraag hier moet of eerder in bèta overig, dus zeg het maar als dit het verkeerde topic is.
f(n) + g(n) = Θ(min(f(n), g(n))) bewijzen of ontkrachten
Bedoelen ze hier met min(f(n), g(n)) de functie van g(n) en f(n) die asymptotisch het kleinste is (oftewel het minst hard stijgt)?
Er staat geen verdere uitleg in het boek, althans niet waar ik het kan vinden (boek is meer dan 1800 pagina's). Ik weet btw niet echt of deze vraag hier moet of eerder in bèta overig, dus zeg het maar als dit het verkeerde topic is.
Finally, someone let me out of my cage
Wat de precieze definitie is kan ik ook niet zeggen, maar het ontkrachten van de bewering zal daar ook niet zo van afhangen.quote:
kleine vraag. Ik moet
f(n) + g(n) = Θ(min(f(n), g(n))) bewijzen of ontkrachten
Bedoelen ze hier met min(f(n), g(n)) de functie van g(n) en f(n) die asymptotisch het kleinste is (oftewel het minst hard stijgt)?
Er staat geen verdere uitleg in het boek, althans niet waar ik het kan vinden (boek is meer dan 1800 pagina's). Ik weet btw niet echt of deze vraag hier moet of eerder in bèta overig, dus zeg het maar als dit het verkeerde topic is.
Mmm, ik kan even geen andere manier bedenken dan allebei de manieren ontkrachtenquote:Op donderdag 30 juni 2011 19:05 schreef Wolfje het volgende:
[..]
Wat de precieze definitie is kan ik ook niet zeggen, maar het ontkrachten van de bewering zal daar ook niet zo van afhangen.
(en welkom terug, want je bent blijkbaar weggeweest
)
Finally, someone let me out of my cage
Met min(f(n), g(n)) wordt de functie bedoeld die elke n naar het minimum van de twee waarden f(n) en g(n) stuurt. "Asymptotisch het kleinste" hoeven ze geen van beide te zijn; ze zouden elkaar oneindig vaak af kunnen wisselen qua groei.quote:
kleine vraag. Ik moet
f(n) + g(n) = Θ(min(f(n), g(n))) bewijzen of ontkrachten
Bedoelen ze hier met min(f(n), g(n)) de functie van g(n) en f(n) die asymptotisch het kleinste is (oftewel het minst hard stijgt)?
Er staat geen verdere uitleg in het boek, althans niet waar ik het kan vinden (boek is meer dan 1800 pagina's). Ik weet btw niet echt of deze vraag hier moet of eerder in bèta overig, dus zeg het maar als dit het verkeerde topic is.
Dankje! Ik moet even wat moeite doen om het idee te begrijpen, maar ik denk dat het wel lukt vanaf hier.quote:
[..]
Met min(f(n), g(n)) wordt de functie bedoeld die elke n naar het minimum van de twee waarden f(n) en g(n) stuurt. "Asymptotisch het kleinste" hoeven ze geen van beide te zijn; ze zouden elkaar oneindig vaak af kunnen wisselen qua groei.
Finally, someone let me out of my cage
Ik heb morgen een wiskunde toets en ik ben nu sommetjes aan het oefenen. Nu ben ik bezig met de volgende som:
Volgens mij moet ik hier de verdubbelingsformules gebruiken maar ik heb geen idee hoe ik dit kan toepassen. Helaas heb ik hier ook geen uitwerking van dus is er iemand die mij op de goede weg kan helpen?
Volgens mij moet ik hier de verdubbelingsformules gebruiken maar ik heb geen idee hoe ik dit kan toepassen. Helaas heb ik hier ook geen uitwerking van dus is er iemand die mij op de goede weg kan helpen?
Neem het leven niet te serieus, je overleeft het toch niet.
Haakjes wegwerken en sin²+cos²=1 toepassen, meer is 't niet.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
De variabele X is in een bepaalde populatie exact normaal verdeeld met een gemiddelde van 10 en een standaarddeviatie van 5. Het plan is om onafhankelijk van elkaar 25 waarnemingen van X te verkrijgen en het gemiddelde "X" te berekenen. Wat is de steekproevenverdeling van "X"
Het goede antwoord is:
Exact normaal verdeeld met gemiddelde 10 en standaarddeviatie 1
Ik snap dit niet. Iemand?
Het goede antwoord is:
Exact normaal verdeeld met gemiddelde 10 en standaarddeviatie 1
Ik snap dit niet. Iemand?
Same shit different day
Er wordt naar de verdeling van het gemiddelde van 25 waarnemingen gevraagd, geef dit aan met de variable Y (die ''X'' is te verwarrend). Elk van de waarnemingen X_i is verdeeld volgens X en onafhankelijk van elkaar. De verdeling van Y is dan (gebruik formule voor lineaire combinatie van onafhankelijke variabelen)quote:Op maandag 4 juli 2011 11:05 schreef Desdemona het volgende:
De variabele X is in een bepaalde populatie exact normaal verdeeld met een gemiddelde van 10 en een standaarddeviatie van 5. Het plan is om onafhankelijk van elkaar 25 waarnemingen van X te verkrijgen en het gemiddelde "X" te berekenen. Wat is de steekproevenverdeling van "X"
Het goede antwoord is:
Exact normaal verdeeld met gemiddelde 10 en standaarddeviatie 1
Ik snap dit niet. Iemand?
Y = (som X_i )/25 ~ N((som mu_i)/25, som sigma_i^2/(25^2)) ~ N(10, (som 1/25)) ~ N(10,1)
Dank voor je reactie en je uitleg!quote:
[..]
Er wordt naar de verdeling van het gemiddelde van 25 waarnemingen gevraagd, geef dit aan met de variable Y (die ''X'' is te verwarrend). Elk van de waarnemingen X_i is verdeeld volgens X en onafhankelijk van elkaar. De verdeling van Y is dan (gebruik formule voor lineaire combinatie van onafhankelijke variabelen)
Y = (som X_i )/25 ~ N((som mu_i)/25, som sigma_i^2/(25^2)) ~ N(10, (som 1/25)) ~ N(10,1)
Same shit different day
Een groep van 18 personen verdeeld zich over drie tafels van 4, 6 en 8 plaatsen. Hoeveel verschillende arrangements zijn er, als de plaatsing aan een tafel geen rol speelt?
Is dat 18! ?
Of bedoelen ze dat er ook 0 personen kunnen worden geplaatst?
Is dat 18! ?
Of bedoelen ze dat er ook 0 personen kunnen worden geplaatst?
Noem de tafel waar 4 mensen kunnen zitten tafel 1, 6 mensen -> tafel 2, 8 mensen -> tafel 3.
Voor tafel 1 zijn er 18 nCr 4 combinaties. Dan zijn er nog 14 mensen over. Aan tafel twee zijn dan nog 14 nCr 8 combinaties. De mensen die overblijven moeten sowieso naar tafel 3, dus dat is 1 combinatie. Dan krijg je in totaal dat het aantal mogelijkheden gelijk is aan (18 nCr 4) * (14 nCr 8)*1.
Als je 18 éénpersoonstafels had gehad dan was het 18! geweest. En alle mensen moeten geplaatst worden.
Voor tafel 1 zijn er 18 nCr 4 combinaties. Dan zijn er nog 14 mensen over. Aan tafel twee zijn dan nog 14 nCr 8 combinaties. De mensen die overblijven moeten sowieso naar tafel 3, dus dat is 1 combinatie. Dan krijg je in totaal dat het aantal mogelijkheden gelijk is aan (18 nCr 4) * (14 nCr 8)*1.
Als je 18 éénpersoonstafels had gehad dan was het 18! geweest. En alle mensen moeten geplaatst worden.
Ja dat had ik eerst, maar ze kunnen toch ook binnen de tafels nog op verschillende stoelen gaan zitten?
De 8 mensen die overblijven kunnen toch op 8! mogelijkheden gaan zitten?quote:De mensen die overblijven moeten sowieso naar tafel 3, dus dat is 1 combinatie.
Dat bedoelen ze waarschijnlijk met "als de plaatsing aan een tafel geen rol speelt", het maakt dus niet uit wie er precies op welke stoel gaat zitten, het gaat er alleen om welke mensen aan welke tafel gaan zitten.quote:
Ja dat had ik eerst, maar ze kunnen toch ook binnen de tafels nog op verschillende stoelen gaan zitten?
[..]
De 8 mensen die overblijven kunnen toch op 8! mogelijkheden gaan zitten?
The biggest argument against democracy is a five minute discussion with the average voter.
Omg ja tuurlijkquote:
[..]
Dat bedoelen ze waarschijnlijk met "als de plaatsing aan een tafel geen rol speelt", het maakt dus niet uit wie er precies op welke stoel gaat zitten, het gaat er alleen om welke mensen aan welke tafel gaan zitten.
, ok duidelijk 
Even voor de duidelijkheid, als het wel uitmaakt is het 18! toch?
Oftewel ((18nCr4)*4!)*((14nCr6)*6!)*((8nCr8)*8!)
