SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
• http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Een uitleg over LaTeX-code kun je hier vinden, en je kunt deze site gebruiken om een hele post met verschillende stukken Latex-code erin ineens te laten parsen door betahw.mine.nu.
Wiskundig inhoudelijk:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
• http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Een uitleg over LaTeX-code kun je hier vinden, en je kunt deze site gebruiken om een hele post met verschillende stukken Latex-code erin ineens te laten parsen door betahw.mine.nu.
Wiskundig inhoudelijk:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
"Als de matrix A(n x n) inverteerbaar is, dan rk(A)=n. "
Dit komt omdat de matrix als een lineaire afbeelding valt te zien, waarvoor je dus een bijectie moet hebben als die inverteerbaar is?
Dit komt omdat de matrix als een lineaire afbeelding valt te zien, waarvoor je dus een bijectie moet hebben als die inverteerbaar is?
Ja, als de rank kleiner dan n is, heb je een afhankelijkheid in de kolommen van A. De kolommen spannen de beeld ruimte op en dan zou je dus een niet lege kern hebben, maar dat is dan strijdig met de inverteerbaarheid.quote:Op zondag 29 mei 2011 10:34 schreef Siddartha het volgende:
"Als de matrix A(n x n) inverteerbaar is, dan rk(A)=n. "
Dit komt omdat de matrix als een lineaire afbeelding valt te zien, waarvoor je dus een bijectie moet hebben als die inverteerbaar is?
Ik ben bezig met integraalrekenen en heb een vraag over het bereken van de lengte van een grafiek. Via mijn grafische rekenmachine kan ik berekeningen maken met behulp van de zogeheten integraalfunctie. Deze functie gebruik ik alleen om te controleren, aangezien ik de berekeningen tot noch toe met behulp van primitieven deed. Echter ben ik nu bezig met het berekenen van de lengte van een grafiek en er staat niet in mijn boek hoe ik die via de rekenkundige weg kan doen. Ik weet dat de integraal de volgende vorm heeft:
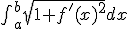
Ik wil deze berekening eigenlijk ook handmatige doen zoals bij het berekenen van een lichaam. Zo gebruik ik bij het berekenen van het volume van een lichaam de volgende integraal:
Deze berekening doe ik dan zo: ( G(b)2 - G(a)2 ) - (H(b)2 - H(a)2) In het geval van de lengte van een grafiek weet ik echter niet welke vorm en welke stappen ik moet volgen. Iemand een idee hoe ik deze berekening kan doen?
Ik wil deze berekening eigenlijk ook handmatige doen zoals bij het berekenen van een lichaam. Zo gebruik ik bij het berekenen van het volume van een lichaam de volgende integraal:
Deze berekening doe ik dan zo: ( G(b)2 - G(a)2 ) - (H(b)2 - H(a)2) In het geval van de lengte van een grafiek weet ik echter niet welke vorm en welke stappen ik moet volgen. Iemand een idee hoe ik deze berekening kan doen?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Je rekenmachine kan f'(x) numeriek bepalen, een TI bijvoorbeeld met de functie nDeriv.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Die functie gebruik ik altijd voor het controleren van mijn afgeleiden. Mijn vraag is of er een berekening bestaat voor het exact bepalen van de lengte van een (stuk van een) grafiek.quote:
Je rekenmachine kan f'(x) numeriek bepalen, een TI bijvoorbeeld met de functie nDeriv.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Dat lijkt me toch niet helemaal correct. Als G(x) een primitieve van g(x) is, dan is G(x)2 in het algemeen geen primitieve van g(x)2.quote:
Ik wil deze berekening eigenlijk ook handmatige doen zoals bij het berekenen van een lichaam. Zo gebruik ik bij het berekenen van het volume van een lichaam de volgende integraal:
[ afbeelding ]
Deze berekening doe ik dan zo: ( G(b)2 - G(a)2 ) - (H(b)2 - H(a)2) In het geval van de lengte van een grafiek weet ik echter niet welke vorm en welke stappen ik moet volgen. Iemand een idee hoe ik deze berekening kan doen?
Dat zal van de functie afhangen. Niet elke functie is primitiveerbaar in termen van `elementaire' functies.quote:
[..]
Die functie gebruik ik altijd voor het controleren van mijn afgeleiden. Mijn vraag is of er een berekening bestaat voor het exact bepalen van de lengte van een (stuk van een) grafiek.
Feitelijk is het de primitieve van een gekwadrateerde functie. Ik weet niet hoe die notatie precies moet zijn.quote:
[..]
Dat lijkt me toch niet helemaal correct. Als G(x) een primitieve van g(x) is, dan is G(x)2 in het algemeen geen primitieve van g(x)2.
Ja dat geloof ik graag. Misschien doe ik te moeilijk voor het niveau (Wiskunde B VWO) maar ik vind het gewoon fijn om het rekenkundig te doen.quote:
[..]
Dat zal van de functie afhangen. Niet elke functie is primitiveerbaar in termen van `elementaire' functies.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Je kunt gewoon sqrt(1+f'(x)²) uitwerken eerst. Om bij jouw voorbeeld aan te haken: als f=g dan pak je het toch ook anders aan dan je nu aangeeft?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Als je op een proefwerk een functie moet primitiveren, dan is het feit dat die opgave in een proefwerk zit al een teken dat het makkelijk is. Als je moeilijk gaat lopen doen, weet je vrij zeker dat je een verkeerde weg inslaat.quote:
[..]
Ja dat geloof ik graag. Misschien doe ik te moeilijk voor het niveau (Wiskunde B VWO) maar ik vind het gewoon fijn om het rekenkundig te doen.
Dat snap ik en erken ik wel. Ik denk ook niet dat het noodzakelijk is, maar ik vind het ook gewoon interessant.quote:Op zondag 29 mei 2011 13:38 schreef thabit het volgende:
[..]
Als je op een proefwerk een functie moet primitiveren, dan is het feit dat die opgave in een proefwerk zit al een teken dat het makkelijk is. Als je moeilijk gaat lopen doen, weet je vrij zeker dat je een verkeerde weg inslaat.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
De uitdrukking die je hierboven geeft voor de booglengte van de grafiek van de functie y = f(x) over het interval [a,b] is exact, maar zoals hier al is opgemerkt is van lang niet elke 'elementaire' functie een primitieve ook in 'elementaire' functies uit te drukken. Zelfs heel 'omschuldig' uitziende functies als ex/x of 1/ln(x) zijn niet in termen van 'elementaire' functies te primitiveren. Als je dus een opgave krijgt waarbij je een booglengte (of: de oppervlakte van een omwentelingslichaam) moet berekenen met een integraal, dan mag je er van uit gaan dat dat ook in termen van elementaire functies is op te lossen. Maar, dat wordt al gauw heel lastig. Probeer maar eens of je bijvoorbeeld de lengte van het paraboolsegment y = ½x2 over het interval [0, 1] exact kunt bepalen (maar dit behoort dacht ik niet tot de stof die je geacht wordt te bestuderen).quote:
[..]
Die functie gebruik ik altijd voor het controleren van mijn afgeleiden. Mijn vraag is of er een berekening bestaat voor het exact bepalen van de lengte van een (stuk van een) grafiek.
[ Bericht 0% gewijzigd door Riparius op 29-05-2011 16:18:07 ]
Je bedoelt dat ik dus met behulp van de integraalfunctie op mijn rekenmachine een antwoord krijg (namelijk ongeveer 1,15), maar dat dit exact erg lastig is te bepalen? Ik zou niet weten hoe in ieder geval.quote:
[..]
De uitdrukking die je hierboven geeft voor de booglengte van de grafiek van de functie y = f(x) over het interval [a,b] is exact, maar zoals hier al is opgemerkt is van lang niet van elke 'elementaire' functie een primitieve ook in 'elementaire' functies uit te drukken. Zelfs heel 'omschuldig' uitziende functies als ex/x of 1/ln(x) zijn niet in termen van 'elementaire' functies te primitiveren. Als je dus een opgave krijgt waarbij je een booglengte (of: de oppervlakte van een omwentelingslichaam) moet berekenen met een integraal, dan mag je er van uit gaan dat dat ook in termen van elementaire functies is op te lossen. Maar, dat wordt al gauw heel lastig. Probeer maar eens of je bijvoorbeeld de lengte van het paraboolsegment y = ½x2 over het interval [0, 1] exact kunt bepalen (maar dit behoort dacht ik niet tot de stof die je geacht wordt te bestuderen).
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Inderdaad. Het exacte antwoord is ∫01 √(1 + x2)dx = ½∙√2 + ½∙ln(1 + √2). Maar om dit te vinden moet je een substitutiemethode gebruiken. Vaak wordt bij dit soort integralen een goniometrische substitutie aangeraden, maar dat levert hier een integraal op die nog steeds erg lastig is. Veel beter is hier een hyperbolische substitutie, maar dan moet je wel weten wat hyperbolische functies zijn (en hun inversen) en wat identiteiten daarvan weten te benutten. Ook kun je een combinatie van partiële integratie en een algebraïsche substitutie gebruiken.quote:
[..]
Je bedoelt dat ik dus met behulp van de integraalfunctie op mijn rekenmachine een antwoord krijg (namelijk ongeveer 1,15), maar dat dit exact erg lastig is te bepalen? Ik zou niet weten hoe in ieder geval.
De lege verzameling.quote:Op zondag 29 mei 2011 17:01 schreef Dale. het volgende:
Als B = {1,4}. Wat is dan het cartesisch product van B×∅? Gewoon B?
The biggest argument against democracy is a five minute discussion with the average voter.
Is dat een 0/empty?quote:
Als B = {1,4}. Wat is dan het cartesisch product van B×∅? Gewoon B?
Zo ja, dan {} lijkt me
Zie hier 
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Eerste stap van mijn oplossing:
Klopt het voorbeeld hieronder en moet ik de opgave hierboven op een identieke manier oplossen?
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Je voorbeeld klopt, maar je eigen notatie niet, immers i is je index, niet n. Je moet de termen van je som dus als e1/i schrijven.quote:
[ afbeelding ]
Eerste stap van mijn oplossing:
[ afbeelding ]
Klopt het voorbeeld hieronder en moet ik de opgave hierboven op een identieke manier oplossen?
[ afbeelding ]
Misschien moet je eventjes je beeldscherm vergroten.quote:
[..]
Je voorbeeld klopt, maar je eigen notatie niet, immers i is je index, niet n. Je moet de termen van je som dus als e1/i schrijven.
Ah, zo. Ik zie het écht niet op de normale resolutie, dan lijkt het hier beslist 1/n. Maar de exponent is dus i/n. Mea culpa (of die van Latex ...).quote:
[..]
Misschien moet je eventjes je beeldscherm vergroten.
Kan gebeuren. 
Het lukt mij bij deze opgave niet om die exponent zodanig te manipuleren dat ik de standaardvorm` krijg waarvoor ik die formule kan gebruiken.
Als die exponent i+5 of iets dergelijks zou zijn dan zou ik het wel weten maar hoe kan je het nu oplossen?
[ Bericht 27% gewijzigd door Bram_van_Loon op 29-05-2011 18:34:50 ]
Het lukt mij bij deze opgave niet om die exponent zodanig te manipuleren dat ik de standaardvorm` krijg waarvoor ik die formule kan gebruiken.
Als die exponent i+5 of iets dergelijks zou zijn dan zou ik het wel weten maar hoe kan je het nu oplossen?
[ Bericht 27% gewijzigd door Bram_van_Loon op 29-05-2011 18:34:50 ]
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Wel, je hebt ei/n = (e1/n)i dus het zijn gewoon termen van een meetkundige rij.quote:
Kan gebeuren.
Het lukt mij bij deze opgave niet om die exponent zodanig te manipuleren dat ik de standaardvorm` krijg waarvoor ik die formule kan gebruiken.
Als die exponent i+5 of iets dergelijks zou zijn dan zou ik het wel weten maar hoe kan je het nu oplossen?
Weer een vraagje van Knuth the art of computer programming. Over het algorithme om getallen te delen.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Wat bedoelen ze bij stap D4 metquote:The digits (u_(j+n), u_(j+n-1), ..., u_j)_b should be kept positive; if the result of this step is actually negative, (u_(n+j), u_(j+n-1), ..., u_j)_b should be left as the true value plus b^(n+1), namely as the b's complement of the true value, and a 'borrow' to the left should be rememberd.
quote:Op zondag 29 mei 2011 18:38 schreef Dale. het volgende:
Weer een vraagje van Knuth the art of computer programming. Over het algorithme om getallen te delen.Dat als er een negatief getal uitkomt (wat mogelijk is, aangezien je het quotient slechts benadert in Stap D3) dat je er dan bn+1 bij op moet tellen, maar dat je dat dan wel moet onthouden.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Wat bedoelen ze bij stap D4 met
[..]
Ok maar waarom moet je dit dan onthouden als het vervolgens bij stap D6 weer uitgecanceld wordt? "(A carry will occur to the left of u_(j+n) ... occured in D4.)"quote:
[..]
Dat als er een negatief getal uitkomt (wat mogelijk is, aangezien je het quotient slechts benadert in Stap D3) dat je er dan bn+1 bij op moet tellen, maar dat je dat dan wel moet onthouden.
"Decrease qj by 1" is waar het om gaat.quote:
[..]
Ok maar waarom moet je dit dan onthouden als het vervolgens bij stap D6 weer uitgecanceld wordt? "(A carry will occur to the left of u_(j+n) ... occured in D4.)"
Ja ok dat is hetzelfde aangezien die hele stap D6 alleen uitgevoerd moet worden wanneer uit D4 negatief kwam.quote:
http://www.wolframalpha.c(...)*%28x%2B2%29%29%2Cx]quote:Op zondag 29 mei 2011 20:40 schreef .aeon het volgende:
klopt het dat de afgeleide van
sin(((x+1)^2)*(x+2))
=
cos((x+1)^2(x+2))*(3x^2+8x+5)
haha faal ²quote:
http://www.wolframalpha.com/input/?i=d%2Fdx+sin%28%28%28x%2B1%29^2%29*%28x%2B2%29%29+
te laat
Ghehehehequote:
[..]
http://www.wolframalpha.c(...)*%28x%2B2%29%29%2Cx]
Op 
Ik denk dat ik het heb uitgewerkt.quote:
[..]
Wel, je hebt ei/n = (e1/n)i dus het zijn gewoon termen van een meetkundige rij.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Ik heb deze vraag bij school/studie gesteld, maar het lijkt me dat het hier hoort, dus bij deze:
Even een zeer specifieke vraag:
Heeft iemand een idee wat het betekend wanneer je met spss een trend analyse doet d.m.v. generalized linear model en daarbij polynominal contrasten laat berekenen, waarbij dan vervolgens bijv. de 1e, 2e, 5e en 6e order significant zijn, maar 8,9,10 bijvoorbeeld niet?
Even een zeer specifieke vraag:
Heeft iemand een idee wat het betekend wanneer je met spss een trend analyse doet d.m.v. generalized linear model en daarbij polynominal contrasten laat berekenen, waarbij dan vervolgens bijv. de 1e, 2e, 5e en 6e order significant zijn, maar 8,9,10 bijvoorbeeld niet?
http://altdating.fluodelic.com (nu nog) gratis datingsite voor mensen met een alternatieve smaak. Help (de webmaster en mij ook) mee om het er leuker te maken en registreer je.
Dat kan niet kloppen wat je daar met die breuk doet. Je zou voor de som uit moeten komen op:quote:
(e(n+1)/n - 1)/(e1/n - 1)
Ja, ik ben vergeten in de noemer die -1 toe te voegen, gewoon een slordigheidje bij het invoeren van de code die ik over het hoofd zag.
Mijn teller is identiek aan die van jou maar het is bij een klein scherm moeilijk te zien wat nog de exponent is en wat niet. De exponent in mijn teller is 1+1/n waar jij (n+1)/n
Mijn teller is identiek aan die van jou maar het is bij een klein scherm moeilijk te zien wat nog de exponent is en wat niet. De exponent in mijn teller is 1+1/n waar jij (n+1)/n
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Zo klopt het wel ja. Maar je doet wat moeilijk bij het sommeren van een meetkundige rij. De som van een aantal opeenvolgende termen van een meetkundige rij is gelijk aan de eerstvolgende term min de eerste term, en dat verschil gedeeld door de reden min één.quote:
Ja, ik ben vergeten in de noemer die -1 toe te voegen, gewoon een slordigheidje bij het invoeren van de code die ik over het hoofd zag.
[ afbeelding ]
Hier is de eerste term (e1/n)0 = 1, de eerstvolgende term (e1/n)n+1, en de reden e1/n, zodat ik meteen uit het blote hoofd zie dat de som (e(n+1)/n - 1)/(e1/n - 1) moet zijn.
Ik dien eerst te bewijzen dat een will. vereniging van C_i's weer gesloten is?quote:
[..]
Sterker nog, hun afsluitingen moeten zelfs disjunct zijn.
Misschien kun je, uitgaande van die Urysohnfuncties die je voor elk tweetal hebt, een functie f: T -> R proberen te maken met f(Ci) = {i} voor elke i.
*EDIT* Dit idee is iets te simpel. Je kunt beginnen met bewijzen dat een willekeurige vereniging van Ci'tjes gesloten is.
Voor eindig veel gaat dit sowieso op. Dus moet het bewijzen voor het aftelbare geval. Moet ik dan kijken naar het complement, dus T minus de aftelbare verzameling van C_i's en bewijzen dat dat een open verzameling is.
Het is in ieder geval de doorsnede van een aantal open verzamelingen,( T\C_1, T\C_2,...). Maar als dat er aftelbaar veel zijn, dan loop ik weeer vast...?
In het algemeen is een aftelbare vereniging van gesloten verzamelingen ook niet gesloten; je moet de eigenschap die in de opgave gegeven is gebruiken.quote:
[ afbeelding ]
[..]
Ik dien eerst te bewijzen dat een will. vereniging van C_i's weer gesloten is?
Voor eindig veel gaat dit sowieso op. Dus moet het bewijzen voor het aftelbare geval. Moet ik dan kijken naar het complement, dus T minus de aftelbare verzameling van C_i's en bewijzen dat dat een open verzameling is.
Het is in ieder geval de doorsnede van een aantal open verzamelingen,( T\C_1, T\C_2,...). Maar als dat er aftelbaar veel zijn, dan loop ik weeer vast...?
Oké, ik heb inmiddels bewezen dat de verenging van aftelbare gesloten verzamelingen gesloten is, wanneer deze onderling disjunct zijn.quote:
[..]
In het algemeen is een aftelbare vereniging van gesloten verzamelingen ook niet gesloten; je moet de eigenschap die in de opgave gegeven is gebruiken.
Wat de C_i'tjes zijn (staat in de opdracht). Nu (als het niet te veel gevraagd is hoor) een hintje naar wat je wilde dat ik hier mee doe...
Oké, ik heb inmiddels bewezen dat de verenging van aftelbare gesloten verzamelingen gesloten is, wanneer deze onderling disjunct zijn. Wat de C_i'tjes zijn (staat in de opdracht). Nu (als het niet te veel gevraagd is hoor) een hintje naar wat je wilde dat ik hier mee doe...
[ Bericht 31% gewijzigd door Hypnagogia op 30-05-2011 19:12:46 (:')) ]
Wat de C_i'tjes zijn (staat in de opdracht). Nu (als het niet te veel gevraagd is hoor) een hintje naar wat je wilde dat ik hier mee doe...[ Bericht 31% gewijzigd door Hypnagogia op 30-05-2011 19:12:46 (:')) ]
Dat geldt in het algemeen niet voor topologische ruimten.quote:Op maandag 30 mei 2011 19:11 schreef TheLoneGunmen het volgende:
[..]
Oké, ik heb inmiddels bewezen dat de verenging van aftelbare gesloten verzamelingen gesloten is, wanneer deze onderling disjunct zijn.
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |