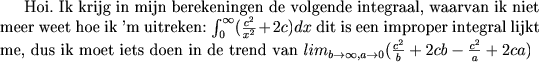SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
De vectoren in V hebben drie componenten, d.w.z. ze zitten in |R³ en niet in |R². Maar de vectoren in V spannen een tweedimensionaal vlak op. Als je een papiertje in de lucht houdt dan heeft iedere papiermolecuul ook drie ruimtelijke componenten (x,y,z), ook al liggen ze allemaal in een tweedimensionaal vlak. 
[ Bericht 13% gewijzigd door BasementDweller op 31-12-2010 17:13:35 ]
[ Bericht 13% gewijzigd door BasementDweller op 31-12-2010 17:13:35 ]
Die vergelijking volg ik als de 3-de component (z in dit geval) een vast getal is. Maar nu hangt z af van x en y, dan ziet de ruimte toch anders uit?quote:Op vrijdag 31 december 2010 16:58 schreef BasementDweller het volgende:
De vectoren in V hebben drie componenten, d.w.z. ze zitten in |R³ en niet in |R². Maar de vectoren in V spannen een tweedimensionaal vlak op. Als je een papiertje in de lucht houdt dan heeft iedere papiermolecuul ook drie ruimtelijke componenten (x,y,z), ook al liggen ze allemaal in een tweedimensionaal vlak.
Je kan de basis zo kiezen dat je blaadje bijvoorbeeld in het x,y-vlak ligt en dus z constant is, maar dat hoeft niet. Als je je blaadje 'schuin' houdt t.o.v. van de basis, dan zijn de x,y en z component variabel. Je hebt dus een twee dimensionaal vlak in een driedimensionale ruimte waarbij alle 3 componenten variabel zijn. Dit is ook het geval bij V.quote:
[..]
Die vergelijking volg ik als de 3-de component (z in dit geval) een vast getal is. Maar nu hangt z af van x en y, dan ziet de ruimte toch anders uit?
Ok, denk dat ik me er nu beter een voorstelling van kan maken. Bedankt!quote:
[..]
Je kan de basis zo kiezen dat je blaadje bijvoorbeeld in het x,y-vlak ligt en dus z constant is, maar dat hoeft niet. Als je je blaadje 'schuin' houdt t.o.v. van de basis, dan zijn de x,y en z component variabel. Je hebt dus een twee dimensionaal vlak in een driedimensionale ruimte waarbij alle 3 componenten variabel zijn. Dit is ook het geval bij V.
Als in het vlak de z-component vast is, is het ook een deelruimte van IR³.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
De beste wensen voor alle mensen!
Ik heb weer een vraag over krommen. Als een kromme X over K (char K > 0, alg afgesloten) geslacht g=1 heeft. Dan heeft X gonaliteit 2. Er is een unieke divisoren klasse met graad 2 en dimensie 1. De overige klassen met graad 2 hebben ieder precies 1 effectieve divisor.
Mijn vraag gaat over krommen met 'willekeurige' gonaliteit y. We weten dat er een unieke divisoren klasse met graad y en dimensie 1 bestaat. Hoeveel effectieve divisoren hebben de overige klassen met graad y? Hebben ze ook weleens ieder precies 1 effectieve divisor? Hoe kan je inzien of je er 1 of eindig veel of oneindig veel klassen hebt?
hartelijk dank.
[ Bericht 5% gewijzigd door simounadi op 02-01-2011 18:31:01 ]
Ik heb weer een vraag over krommen. Als een kromme X over K (char K > 0, alg afgesloten) geslacht g=1 heeft. Dan heeft X gonaliteit 2. Er is een unieke divisoren klasse met graad 2 en dimensie 1. De overige klassen met graad 2 hebben ieder precies 1 effectieve divisor.
Mijn vraag gaat over krommen met 'willekeurige' gonaliteit y. We weten dat er een unieke divisoren klasse met graad y en dimensie 1 bestaat. Hoeveel effectieve divisoren hebben de overige klassen met graad y? Hebben ze ook weleens ieder precies 1 effectieve divisor? Hoe kan je inzien of je er 1 of eindig veel of oneindig veel klassen hebt?
hartelijk dank.
[ Bericht 5% gewijzigd door simounadi op 02-01-2011 18:31:01 ]
Is het dan niet 'triviaal' ?quote:Op zondag 2 januari 2011 13:18 schreef GlowMouse het volgende:
Als in het vlak de z-component vast is, is het ook een deelruimte van IR³.
Omdat R2 altijd een deelruimte is van R3, alleen meestal in punt [0].
Even 'triviaal' als elke andere lineaire deelruimte, het is gewoon een kwestie van de definitie gebruiken. De vz. V={(a 0 0)T | a \in R} is ook een lineaire deelruimte bijv., of V={(a 0 b)T | a,b \in R}.quote:
[..]
Is het dan niet 'triviaal' ?
Omdat R2 altijd een deelruimte is van R3, alleen meestal in punt [0].
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
R² is geen deelruimte van R³ omdat een element uit R² niet in R³ zit (hij mist een component, die kun je niet op 0 denken).quote:
[..]
Is het dan niet 'triviaal' ?
Omdat R2 altijd een deelruimte is van R3, alleen meestal in punt [0].
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Wel isomorf?quote:
[..]
R² is geen deelruimte van R³ omdat een element uit R² niet in R³ zit (hij mist een component, die kun je niet op 0 denken).
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Wikipedia zegt 't al: Twee eindig-dimensionale vectorruimten zijn isomorf als en slechts als hun dimensies gelijk zijn.quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik zit met de volgende vraag:
If X has a normal distribution with mean 60 and standard deviation 6, which value of X
corresponds with the value z = 1.96?
Het antwoord is x = 71.76.
Nou dacht ik dat je de standardized test statistic moest gebruiken:
z = x - μ / (sigma/√n)
Maar dan ontbreekt natuurlijk de n waardoor je het niet kan berekenen. Ik zie in dat ze 1.96*6+60 doen. Dit maakt de formule z = x - μ / sigma, ik snap alleen niet welke formule dit dan is...
If X has a normal distribution with mean 60 and standard deviation 6, which value of X
corresponds with the value z = 1.96?
Het antwoord is x = 71.76.
Nou dacht ik dat je de standardized test statistic moest gebruiken:
z = x - μ / (sigma/√n)
Maar dan ontbreekt natuurlijk de n waardoor je het niet kan berekenen. Ik zie in dat ze 1.96*6+60 doen. Dit maakt de formule z = x - μ / sigma, ik snap alleen niet welke formule dit dan is...
Kort antwoord:
Dit is kansrekening. Test statistics horen bij statistiek.
Iets langer antwoord:
Jouw z hoort bij een gemiddelde uit een normale verdeling. Als je 1000x een gemiddelde berekent, heb je minder spreiding dan wanneer je 1000x een trekking doet uit de normale verdeling. Daarom moet je de standaardafwijking nog delen door n wanneer je een gemiddelde bekijkt.
Dit is kansrekening. Test statistics horen bij statistiek.
Iets langer antwoord:
Jouw z hoort bij een gemiddelde uit een normale verdeling. Als je 1000x een gemiddelde berekent, heb je minder spreiding dan wanneer je 1000x een trekking doet uit de normale verdeling. Daarom moet je de standaardafwijking nog delen door n wanneer je een gemiddelde bekijkt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Misschien als aanvulling op GM: de z-waarde die je gekregen hebt hoor bij een standaard normale verdeling, d.w.z. een normale verdeling met gemiddelde 0 en standaardafwijking 1. Elke normaal verdeelde stochast X met een gemiddelde mu en een standaardafwijking sigma heeft als eigenschap dat de stochast (X-mu)/sigma een standaard normale verdeling volgt. Als je dus een kans oid wilt berekenen voor X kun je het altijd terugbrengen naar een kans voor een standaard normale verdeling en vandaar dat je in de standaard tabellenboeken alleen de kansen voor standaard normale verelingen opgenomen ziet, dat is immers voldoende voor elke normale verdeling.quote:
Ik zit met de volgende vraag:
If X has a normal distribution with mean 60 and standard deviation 6, which value of X
corresponds with the value z = 1.96?
Het antwoord is x = 71.76.
Nou dacht ik dat je de standardized test statistic moest gebruiken:
z = x - μ / (sigma/√n)
Maar dan ontbreekt natuurlijk de n waardoor je het niet kan berekenen. Ik zie in dat ze 1.96*6+60 doen. Dit maakt de formule z = x - μ / sigma, ik snap alleen niet welke formule dit dan is...
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Hallo ik heb enige moeite met deze diff:
Als je die dy/dx oplost gebruik ik dus ln x = 1/x regel. Dan krijg je 15 . 1/x/80 (maar dan zie ik bij de antwoorden dat je nog keer 1/80 moet doen, is dat product regel ofzo?)
Maar daarna d2y/dx2 die vind ik veel moeilijker, die snap ik eigenlijk helemaal niet. Hoe pak je die aan?
Als je die dy/dx oplost gebruik ik dus ln x = 1/x regel. Dan krijg je 15 . 1/x/80 (maar dan zie ik bij de antwoorden dat je nog keer 1/80 moet doen, is dat product regel ofzo?)
Maar daarna d2y/dx2 die vind ik veel moeilijker, die snap ik eigenlijk helemaal niet. Hoe pak je die aan?
Blues ain't nothing but a good man feeling bad...
Voor de eerste krijg je 15*1/x*1/80. Ik begrijp niet helemaal uit je post of dat nu wel of niet in het antwoordenboek staat?quote:
Hallo ik heb enige moeite met deze diff:
[ afbeelding ]
Als je die dy/dx oplost gebruik ik dus ln x = 1/x regel. Dan krijg je 15 . 1/x/80 (maar dan zie ik bij de antwoorden dat je nog keer 1/80 moet doen, is dat product regel ofzo?)
Maar daarna d2y/dx2 die vind ik veel moeilijker, die snap ik eigenlijk helemaal niet. Hoe pak je die aan?
Voor die tweede, is die rho links een constante, en staat in de noemer inderdaad een absolute waarde? Is het de bedoeling om y(x) te vinden?
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Dat heb ik een beetje vaag gezegd, maar je gebruik dus de y functie.
y = 15 ln (x/80)
En daarvan wil ik te weten komen: d2y/dx2 Maar die kwadraten brengen me in de war, ben vergeten hoe dit moet. Dit is namelijk onderdeel van een grotere mechanica som, maar ik kom niet door het wiskundige ervan (ditdus)
y = 15 ln (x/80)
En daarvan wil ik te weten komen: d2y/dx2 Maar die kwadraten brengen me in de war, ben vergeten hoe dit moet. Dit is namelijk onderdeel van een grotere mechanica som, maar ik kom niet door het wiskundige ervan (ditdus)
Blues ain't nothing but a good man feeling bad...
Ok, je krijgt dus dy/dx = 15/(80*x) = (15/80)*x-1. Nog een keer differentieren geeft (15/80)*(-1)*x-2 = -15/80*x-2.quote:
Dat heb ik een beetje vaag gezegd, maar je gebruik dus de y functie.
y = 15 ln (x/80)
En daarvan wil ik te weten komen: d2y/dx2
Edit: die kwadraten staan gewoon voor de tweede afgeleide.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Oooooh, het is zo lang geleden. Jaartje ziek geweest en uit de running dan vergeet je echt alles 
thx men!
thx men!
Blues ain't nothing but a good man feeling bad...
quote:
Oooooh, het is zo lang geleden. Jaartje ziek geweest en uit de running dan vergeet je echt alles
.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Klopt niet. Het moet -15/x2 zijn. Je vergeet de kettingregelquote:Op woensdag 5 januari 2011 16:41 schreef keesjeislief het volgende:
[..]
Ok, je krijgt dus dy/dx = 15/(80*x) = (15/80)*x-1. Nog een keer differentieren geeft (15/80)*(-1)*x-2 = -15/80*x-2.
Edit: die kwadraten staan gewoon voor de tweede afgeleide.
Ik vergat niet de kettingregel maar paste hem verkeerd toe. <font size=463729463>quote:
[..]
Klopt niet. Het moet -15/x2 zijn. Je vergeet de kettingregel
</font>. Je krijgt natuurlijk dy/dx = 15*1/(x/80)*1/80 = 15/x. 
.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Ja! En het tweede wordt dus -15x-2 edit oh wacht dat zegt ie
Blues ain't nothing but a good man feeling bad...
Waar haal je die a en b vandaan?
En volgens mij is dit niet Riemann integreerbaar want 1/x² is onbegrensd op (0,inf).
En volgens mij is dit niet Riemann integreerbaar want 1/x² is onbegrensd op (0,inf).
Hmmm misschien faal ik ook wel ergens eerder: dit is het probleem:
ik wil 2(x+y) differentieren over x en y op het gebied: xy kleiner of gelijk aan c (constante)
Oh nja ik zie al dat ik de integraal beter in 2 stukken kan breken, een van 0 tot 1 en een van 1 tot oneindig. Maar hoe zit het met bijvoorbeeld de integraal van dx op het interval 1 tot oneindig? Daar komt dan oneindig uit... wat ik niet kan gebruiken
[ Bericht 44% gewijzigd door TheLoneGunmen op 07-01-2011 18:02:24 ]
ik wil 2(x+y) differentieren over x en y op het gebied: xy kleiner of gelijk aan c (constante)
Oh nja ik zie al dat ik de integraal beter in 2 stukken kan breken, een van 0 tot 1 en een van 1 tot oneindig. Maar hoe zit het met bijvoorbeeld de integraal van dx op het interval 1 tot oneindig? Daar komt dan oneindig uit... wat ik niet kan gebruiken
[ Bericht 44% gewijzigd door TheLoneGunmen op 07-01-2011 18:02:24 ]
Je wil 2(x+y) differentiëren maar je integreert c²/x² + 2c ?
Ik neem aan dat je integreren bedoelt maar dan snap ik nog niet waarom je dan een andere functie pakt?
Ik neem aan dat je integreren bedoelt maar dan snap ik nog niet waarom je dan een andere functie pakt?
Hoi BD, bedankt voor je reacties; ik bedoel inderdaad integreren. Om het een beetje duidelijk te maken: dit is de hele opgave + mijn poging tot oplossing. Hopelijk kun je me wat op weg helpen:
Je vergeet volgens mij het laatste gedeelte van de eerste zin in je opgave in de rest van je berekening.quote:
Hoi BD, bedankt voor je reacties; ik bedoel inderdaad integreren. Om het een beetje duidelijk te maken: dit is de hele opgave + mijn poging tot oplossing. Hopelijk kun je me wat op weg helpen:
[ afbeelding ]
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!
Held.quote:Op vrijdag 7 januari 2011 21:13 schreef freiss het volgende:
[..]
Je vergeet volgens mij het laatste gedeelte van de eerste zin in je opgave in de rest van je berekening.
Stoned wiskunde opgaven maken, ik dacht dat daardoor alles beter ging.
Nja het lijkt wel in ieder geval
Kijk nu is het al een stuk duidelijker wat je aan het doen bent . Maar is hiermee het probleem opgelost? Want dan heb je toch nog steeds een -t²/0 ?
Gebruik je wel de correcte theorem? Met die theorem bereken je de CDF terwijl je de PDF moet berekenen toch?
[ Bericht 30% gewijzigd door BasementDweller op 07-01-2011 23:06:54 ]
. Maar is hiermee het probleem opgelost? Want dan heb je toch nog steeds een -t²/0 ?Gebruik je wel de correcte theorem? Met die theorem bereken je de CDF terwijl je de PDF moet berekenen toch?
[ Bericht 30% gewijzigd door BasementDweller op 07-01-2011 23:06:54 ]
Ja het móest zelfs met deze theorem werd verteld. Dus via CDF en dan met differentieren naar pdf. Dit is dan gewoon een improper integral type I (wiki) dus dan integreer je van a tot 1 en neem je de limiet van a rechts naar 0.
[ Bericht 39% gewijzigd door TheLoneGunmen op 08-01-2011 00:13:38 ]
[ Bericht 39% gewijzigd door TheLoneGunmen op 08-01-2011 00:13:38 ]
Voor de joint PDF van S en T werkt deze theorem niet. Daarvoor moet je iets doen met de hessiaan van de inversefuncties.
Voor alleen T doe je het bijna goed, alleen heb je f(x,y) verkeerd. Op sommige punten in je gebied is die 0 omdat dan niet geldt dat 0<x<y<1.
Voor alleen T doe je het bijna goed, alleen heb je f(x,y) verkeerd. Op sommige punten in je gebied is die 0 omdat dan niet geldt dat 0<x<y<1.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ah ok. Bedankt. Ik ga er zelf wel even verder mee stoeien vooraleer ik jullie weer lastig val. Heb je toevallig een link naar duidelijke theorie hierover (mag Engels/Nederlands).quote:
Voor de joint PDF van S en T werkt deze theorem niet. Daarvoor moet je iets doen met de hessiaan van de inversefuncties.
Voor alleen T doe je het bijna goed, alleen heb je f(x,y) verkeerd. Op sommige punten in je gebied is die 0 omdat dan niet geldt dat 0<x<y<1.
Het boek van Bain en Engelhardt, maar die theorem lijkt daar ook uit te komen.quote:
[..]
Ah ok. Bedankt. Ik ga er zelf wel even verder mee stoeien vooraleer ik jullie weer lastig val. Heb je toevallig een link naar duidelijke theorie hierover (mag Engels/Nederlands).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Is er een manier om intuïtief in te kunnen zien dat iets uniform convergeert of niet? Ik weet het pas als ik het bewezen heb, anders heb ik geen flauw idee... dus heb er totaal geen intuïtie voor.
Tja, misschien vooral ervaring, maar vaak zie je wel snel of ergens een uniforme schattng op past of niet, ook door te kijken naar de punten waar het evt. mis zou kunnen gaan.quote:
Is er een manier om intuïtief in te kunnen zien dat iets uniform convergeert of niet? Ik weet het pas als ik het bewezen heb, anders heb ik geen flauw idee... dus heb er totaal geen intuïtie voor.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Het moest Jacobiaan zijn. Staat ook wel ergens in B&E.quote:
Hahah klopt, ik vind 'm lelijk. Bedoel je Hessiaan of Jacobiaan?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
