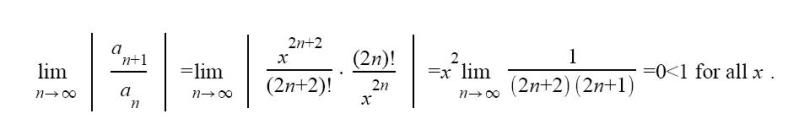SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



- nvm -
[ Bericht 80% gewijzigd door GlowMouse op 22-12-2009 00:28:46 ]
[ Bericht 80% gewijzigd door GlowMouse op 22-12-2009 00:28:46 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik intepreteer |x| altijd als "de lengte van vector x", en wist niet dat het ook "de absolute waarde van" kon betekenen in dit verband. (ik dacht dus eigenlijk dat ik moest laten zien dat als de lengte van een vector niet veranderd na een lineaire transformatie, dat we ofwel te maken hebben met loodrechte spiegeling, of met rotatie)
Maar stel dat bedoeld word dat de absolute waarde van x behouden blijft, dan impliceert dat dat T ofwel de identiteitsmatrix is, of minus de identiteitsmatrix. In het geval dat T de identiteitsmatrix is kan je het opvatten als een rotatie van 2pi, en als het minus de identiteitsmatrix is als spiegeling of rotatie van pi (is dat hetzelfde?).
Kan me haast niet voorstellen dat dit bedoeld wordt
Maar stel dat bedoeld word dat de absolute waarde van x behouden blijft, dan impliceert dat dat T ofwel de identiteitsmatrix is, of minus de identiteitsmatrix. In het geval dat T de identiteitsmatrix is kan je het opvatten als een rotatie van 2pi, en als het minus de identiteitsmatrix is als spiegeling of rotatie van pi (is dat hetzelfde?).
Kan me haast niet voorstellen dat dit bedoeld wordt


Hebben we het over ||Tx|| of over |Tx| (component-wise absolute waarde)?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bij lineaire algebra wordt |x| opgevat als 'de lengte van x' . ||x|| wordt daar nooit gebruikt...quote:Op dinsdag 22 december 2009 00:29 schreef GlowMouse het volgende:
Hebben we het over ||Tx|| of over |Tx| (component-wise absolute waarde)?
Het is me nooit uitgelegd wat het verschil is tussen die twee. Ik dacht dat het een kwestie van verschillende notatie maar zelfde betekenis was.
[ Bericht 8% gewijzigd door BasementDweller op 22-12-2009 00:40:17 ]


heb je algebraïsche eigenschappen geleerd van rotatiematrices/spiegelmatrices?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik vermoed van niet.quote:Op dinsdag 22 december 2009 00:38 schreef GlowMouse het volgende:
heb je algebraïsche eigenschappen geleerd van rotatiematrices/spiegelmatrices?
Er is trouwens een hint:
Laat zien dat Te2 loodrecht staat op Te1
(was misschien handig geweest als ik die er direct had bij gezet, maar ik dacht misschien weet jij een andere manier, want hiermee kwam ik niet verder)


hier heb je al dat T tranpose zijn inverse is, een van de eigenschappen van een rotatiematrix (zie http://en.wikipedia.org/wiki/Rotation_matrix ).
Dat aantonen gaat op dezelfde manier als wat ik juist deed. Hiermee ben je klaarquote:Op dinsdag 22 december 2009 00:41 schreef BasementDweller het volgende:
[..]
Ik vermoed van niet.
Er is trouwens een hint:
Laat zien dat Te2 loodrecht staat op Te1
[ Bericht 50% gewijzigd door motorbloempje op 01-09-2013 21:33:59 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik snap niet wat daar gebeurt en ook niet waarom je het daarmee aantoont... in dit hoofdstuk (waar de vraag bij hoort) worden dit soort dingen niet behandeld. In een volgend hoofdstuk vind ik wel dingen die er een beetje op lijken, maar dat heb ik nog niet bestudeerd. Misschien moet ik dat eerst maar eens gaan doen.... 


misschien dat morgen iemand komt die het sneller/anders ziet 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik zie nu in dat volgende hoofdstuk een stelling staan:
|Ax|=|x| => A(x) dot A(y)= x dot y
Dus omdat e1 dot e2 =0, Te1 dot Te2 = 0. Met behulp van die stelling is het dus erg eenvoudig om te laten zien dat Te2 loodrecht staat op Te1, maar heb ik daarmee dan aangetoond dat T een rotatie of een loodrechte spiegeling is? Zo ja, waarom?
[ Bericht 1% gewijzigd door BasementDweller op 22-12-2009 01:25:12 ]
|Ax|=|x| => A(x) dot A(y)= x dot y
Dus omdat e1 dot e2 =0, Te1 dot Te2 = 0. Met behulp van die stelling is het dus erg eenvoudig om te laten zien dat Te2 loodrecht staat op Te1, maar heb ik daarmee dan aangetoond dat T een rotatie of een loodrechte spiegeling is? Zo ja, waarom?
[ Bericht 1% gewijzigd door BasementDweller op 22-12-2009 01:25:12 ]


intuïtief: alles blijft even lang en er vervormt niks
Je kunt ook zeggen x=x(1)e1 + x(2)e2, dus Tx = x(1) Te1 + x(2) Te2, dus je hebt dezelfde vector maar dan tov een andere orthogonale basis.
Je kunt ook zeggen x=x(1)e1 + x(2)e2, dus Tx = x(1) Te1 + x(2) Te2, dus je hebt dezelfde vector maar dan tov een andere orthogonale basis.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja, intuïtief snap ik het wel. Maar wat het loodrecht staan van de afbeeldingen van e1 en e2 te maken heeft met rotatie/loodrechte spiegeling, is me een raadsel.quote:Op dinsdag 22 december 2009 01:19 schreef GlowMouse het volgende:
intuïtief: alles blijft even lang en er vervormt niks
Je kunt ook zeggen x=x(1)e1 + x(2)e2, dus Tx = x(1) Te1 + x(2) Te2, dus je hebt dezelfde vector maar dan tov een andere orthogonale basis.
Ah, ik snap het al. Als de basis loodrecht blijft na afbeelden, betekent dat dat er geen vervorming is en dan kan je alleen maar roteren of spiegelen. Niet echt een prachtig bewijs, maar ze vragen eigenlijk ook alleen maar 'laat zien' .
Oke bedankt, ik ben eruit
(Wat ik wel slecht vind aan die opgave is dat het met die hint niet hard bewezen is, maar eigenlijk nog steeds vrij intuïtief. En dat terwijl ik het zonder die hint intuïtief ook al prima begrijp. Bovendien had ik er een stelling uit een ander hoofdstuk bij nodig...
[ Bericht 8% gewijzigd door BasementDweller op 22-12-2009 01:36:36 ]


Opnieuw een lineaire algebra vraag:
Zij A: R² -> R² een lineaire afbeelding ongelijk aan O, de nul-afbeelding. Stel M²=O.
(a) Bewijs dat dim(ker(M))=1 (dus de dimensie van de kern van M is gelijk aan 1)
Om dit te bewijzen wou ik gebruik maken van twee matrices. Matrix A heeft één getal in de rechterbovenhoek. Matrix B heeft één getal in de linkerbenedenhoek. Voor die matrices geldt A²=B²=0. Dan is het makkelijk om te te laten zien dat ker(A)= { x¤R² | x =t(1,0), voor alle t¤R} en ker(B)= { x¤R² | x= t (0,1), voor alle t¤R}. Omdat ker(A) en ker(B) één vrijheidsgraad hebben geldt: dim(ker(A))=dim(ker(B))=1.
Echter, bij vraag (c) wordt pas een voorbeeld gevraagd van een dergelijke afbeelding M. Mijn conclusie is dus dat (a) ook in het algemeen bewezen kan worden zonder gebruik te maken van Matrix A en B.
Heeft iemand enig idee hoe?
Zij A: R² -> R² een lineaire afbeelding ongelijk aan O, de nul-afbeelding. Stel M²=O.
(a) Bewijs dat dim(ker(M))=1 (dus de dimensie van de kern van M is gelijk aan 1)
Om dit te bewijzen wou ik gebruik maken van twee matrices. Matrix A heeft één getal in de rechterbovenhoek. Matrix B heeft één getal in de linkerbenedenhoek. Voor die matrices geldt A²=B²=0. Dan is het makkelijk om te te laten zien dat ker(A)= { x¤R² | x =t(1,0), voor alle t¤R} en ker(B)= { x¤R² | x= t (0,1), voor alle t¤R}. Omdat ker(A) en ker(B) één vrijheidsgraad hebben geldt: dim(ker(A))=dim(ker(B))=1.
Echter, bij vraag (c) wordt pas een voorbeeld gevraagd van een dergelijke afbeelding M. Mijn conclusie is dus dat (a) ook in het algemeen bewezen kan worden zonder gebruik te maken van Matrix A en B.
Heeft iemand enig idee hoe?


Je weet dat dim(ker(M)) 0,1 of 2 kan zijn, en 0 en 2 kun je vrij makkelijk wegstrepen (0 omdat de kolommen van m in de nulruimte zitten, 2 omdat het niet de nulmatrix is).
Maar het is ook makkelijk in te zien dat M een lineaire combinatie moet zijn van A en B, en vervolgens dat niet beide gewichten ongelijk aan 0 kunnen zijn.
Maar het is ook makkelijk in te zien dat M een lineaire combinatie moet zijn van A en B, en vervolgens dat niet beide gewichten ongelijk aan 0 kunnen zijn.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Wat bedoel je er precies mee dat de kolommen van M in de nulruimte zitten?quote:Op donderdag 24 december 2009 00:42 schreef GlowMouse het volgende:
Je weet dat dim(ker(M)) 0,1 of 2 kan zijn, en 0 en 2 kun je vrij makkelijk wegstrepen (0 omdat de kolommen van m in de nulruimte zitten, 2 omdat het niet de nulmatrix is).
Maar het is ook makkelijk in te zien dat M een lineaire combinatie moet zijn van A en B, en vervolgens dat niet beide gewichten ongelijk aan 0 kunnen zijn.


M*[eerste kolom van M] = 0. Volgt uit M*M=O.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


En omdat die kolom in de nulruimte zit is de dimensie niet 0? Ik heb erover nagedacht maar zie het verband niet 


We hebben tenminste één niet-nulvector (de linker- of rechterkolom van M) die in de nulruimte(=kern) zit.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Oke, nog een lineaire algebra vraag.
Gegeven: Zij A: Rn -> Rn een lineaire afbeelding met de eigenschap A² = A.
Te bewijzen: Zij V een lineaire deelruimte van Rn. De doorsnede van ker(A) en A(V) is de verzameling bestaande uit slechts de nulvector.
Heb een hint nodig.. ik blijf dit soort opgaves lastig vinden
Gegeven: Zij A: Rn -> Rn een lineaire afbeelding met de eigenschap A² = A.
Te bewijzen: Zij V een lineaire deelruimte van Rn. De doorsnede van ker(A) en A(V) is de verzameling bestaande uit slechts de nulvector.
Heb een hint nodig.. ik blijf dit soort opgaves lastig vinden


-
[ Bericht 100% gewijzigd door GlowMouse op 24-12-2009 16:30:18 ]
[ Bericht 100% gewijzigd door GlowMouse op 24-12-2009 16:30:18 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Neem een element v van Rn dat zowel in ker(A) als A(V) zit. Te bewijzen: v=0. Je weet: Av = 0 en er is een w met v = Aw. Nu jij weer.


Waarom weet ik dat Av=0 ?quote:Op donderdag 24 december 2009 16:27 schreef thabit het volgende:
Neem een element v van Rn dat zowel in ker(A) als A(V) zit. Te bewijzen: v=0. Je weet: Av = 0 en er is een w met v = Aw. Nu jij weer.
Bedoel je dat je Av gelijk kan stellen aan nul omdat A een lineaire afb is?


Ligt het aan mij of heb je ook genoeg aan 'A is vierkant'?
je neemt aan dat hij zit in de doorsnede van ker(A) en A(V).quote:Waarom weet ik dat Av=0 ?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Lineaire afbeeldingen zijn niet vierkant. Maar als je n=2 neemt en A de lineaire afbeelding (x,y) -> (y,0) dan heb je een tegenvoorbeeld want (1,0) zit in zowel kern als beeld.quote:Op donderdag 24 december 2009 16:38 schreef GlowMouse het volgende:
Ligt het aan mij of heb je ook genoeg aan 'A is vierkant'?


ah zie t al, ben in de war met de rijruimte van de matrix die bij de lineaire afbeelding hoort
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik zie niet waarom er een w bestaat z.d.d. v=Aw.
Is het omdat W een deelruimte is van Rn, dat je daardoor Aw gelijk kan stellen aan v omdat v in Rn zit?
Maar als dat zo is. Dan is Av=AAw=Aw=v=0 en ben je klaar
Is het omdat W een deelruimte is van Rn, dat je daardoor Aw gelijk kan stellen aan v omdat v in Rn zit?
Maar als dat zo is. Dan is Av=AAw=Aw=v=0 en ben je klaar


Oke guys. Calculus 11.9. Ik moet nu "use differentation to find a power series representation for:
f(x) = 1/ (1+x)2
Ik heb totaal geen idee hoe het nou wordt omgezet tot een power series. In het boek (blz. 732) staat er wel wat theorie, maar ik kom er niet uit. Zelf aerostudents (handige site), waar de uitwerkingen op staan laten mij in de steek. Wat wordt er precies gebruikt? iets met a/1-r = ar^n-1 iig.
f(x) = 1/ (1+x)2
Ik heb totaal geen idee hoe het nou wordt omgezet tot een power series. In het boek (blz. 732) staat er wel wat theorie, maar ik kom er niet uit. Zelf aerostudents (handige site), waar de uitwerkingen op staan laten mij in de steek. Wat wordt er precies gebruikt? iets met a/1-r = ar^n-1 iig.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Goddeloze mathematici ook altijd. Augustinus zei het al: De goede Christen moet bevreesd zijn voor de mathematici. Op kerstavond! 
Maar, denk ook aan de afgeleide.
Maar, denk ook aan de afgeleide.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Een mooie kerstgedachte.quote:Op donderdag 24 december 2009 23:12 schreef Iblis het volgende:
Maar, denk ook aan de afgeleide.


quote:Op donderdag 24 december 2009 23:09 schreef thabit het volgende:
Ik zou beginnen met 1/(1+x), weet je daar de machtreeksrepresentatie van?
sommatieteken: (-1)^n * x^n lijkt mij ???
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Idd een Christen hahaha. Laat ik dat nou net niet zijnquote:Op donderdag 24 december 2009 23:12 schreef Iblis het volgende:
Goddeloze mathematici ook altijd. Augustinus zei het al: De goede Christen moet bevreesd zijn voor de mathematici. Op kerstavond!
Maar, denk ook aan de afgeleide.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Goed, nu de kerstgedachte toepassen.quote:Op donderdag 24 december 2009 23:14 schreef Burakius het volgende:
[..]
sommatieteken: (-1)^n * x^n lijkt mij ???


Jou helpen.quote:Op donderdag 24 december 2009 23:16 schreef Burakius het volgende:
[..]
Idd een Christen hahaha. Laat ik dat nou net niet zijn. Wat doe jij trouwens hier op dit tijdstip op deze dag
?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Iemand met de naam van de duivel die een Moslim helptquote:
Nederland is té multicultureel hahaha. Je was natuurlijk de hele dag op mij aan het wachten hahaha
hmmm heb jij toevallig een boek van Dostojevski gelezen?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Zeker. Maar dat is denk ik meer voor de alfa-topic.quote:Op donderdag 24 december 2009 23:32 schreef Burakius het volgende:
[..]
Iemand met de naam van de duivel die een Moslim helpt..
Nederland is té multicultureel hahaha. Je was natuurlijk de hele dag op mij aan het wachten hahaha.
hmmm heb jij toevallig een boek van Dostojevski gelezen?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Kijk zonder differntiatie of whatever dat ook moge zijn wat je hier moet doen kom ik tot:quote:Op donderdag 24 december 2009 23:20 schreef thabit het volgende:
[..]
Goed, nu de kerstgedachte toepassen.
f(x) = 1/(1+x)2 --> 1/1+x sommatieteken: 1/1+x ----> 1/1+x sommatieteken: 1/1-(-x)
--> 1/1+x sommatieteken: (-x)n --> 1/1+x sommatieteken: (-1)n * xn
Maar ja..
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Ik snap niet helemaal wat je doet, maar in concreto, merk op:
Voor 1/(1+x) weet je nu al een reeks, en als je die differentieert… dan moet het (bijna) uitkomen.
Voor 1/(1+x) weet je nu al een reeks, en als je die differentieert… dan moet het (bijna) uitkomen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


is dat nou handig, standaardreeksen leren?
f(x) = 1/ (1+x)²
f'(x) = -2/(1+x)³
f''(x) = 6/(1+x)^4
en dan zie je het patroontje:
dus
vul je in in de formule voor de taylorreeks rond x=0 en je bent klaar.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:34:06 ]
f(x) = 1/ (1+x)²
f'(x) = -2/(1+x)³
f''(x) = 6/(1+x)^4
en dan zie je het patroontje:
dus
vul je in in de formule voor de taylorreeks rond x=0 en je bent klaar.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:34:06 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


In mijn lial diktaat staat het volgende:
Stel v=(v1, v2, ... , vn)t. We definiëren v* als de complex geconjugeerde van v. Dan geldt v*tv= (v1² + ... + vn²).
Ik zie niet in waarom dit waar is. Ik krijg: v*tv=(v1*v1 + v2*v2 + ... + vn*vn)
(let op: * betekent de geconjugeerde, niet vermenigvuldiging)
Als tegenvoorbeeld:
Stel dat v1= 1+i, dan is v1*=1-i. Dus v1*v1=(1-i)(1+i)!=(1+i)²=v12
[ Bericht 3% gewijzigd door BasementDweller op 25-12-2009 16:19:46 ]
Stel v=(v1, v2, ... , vn)t. We definiëren v* als de complex geconjugeerde van v. Dan geldt v*tv= (v1² + ... + vn²).
Ik zie niet in waarom dit waar is. Ik krijg: v*tv=(v1*v1 + v2*v2 + ... + vn*vn)
(let op: * betekent de geconjugeerde, niet vermenigvuldiging)
Als tegenvoorbeeld:
Stel dat v1= 1+i, dan is v1*=1-i. Dus v1*v1=(1-i)(1+i)!=(1+i)²=v12
[ Bericht 3% gewijzigd door BasementDweller op 25-12-2009 16:19:46 ]


Zou iemand me kort uit kunnen leggen wat een integraaltransformatie is, ik weet dit niet precies en van wikipedia en google werd ik ook niet veel wijzer. Ik weet wel wat bijvoorbeeld de fourieranalyse is, hoe hij werkt en wat hij doet.
Finally, someone let me out of my cage


Gewoon de afgeleide dus? Sorry als dit geen nut heeft, maar ik heb binnenkort toch een toets over differentieren en integreeren.quote:Op donderdag 24 december 2009 23:05 schreef Burakius het volgende:
Oke guys. Calculus 11.9. Ik moet nu "use differentation to find a power series representation for:
f(x) = 1/ (1+x)2
Ik doe het altijd zo:
f(x) = 1/ (1+x)2 = (1 + x)-2
Deze regel geldt:
f(x) = xa
f'(x) = axa-1
Dus hier:
f(x) = (1 + x)-2
f'(x) = -2 * (1 + x)-3 = -2 * 1 / (1 + x)3 = -2 / (1 + x)3
Finally, someone let me out of my cage


Een fouriertransformatie is een integraaltransformatie, maar er zijn er meerdere. http://nl.wikipedia.org/wiki/Integraaltransformatie is vrij duidelijk wat dat betreft.quote:Op vrijdag 25 december 2009 16:45 schreef minibeer het volgende:
Zou iemand me kort uit kunnen leggen wat een integraaltransformatie is, ik weet dit niet precies en van wikipedia en google werd ik ook niet veel wijzer. Ik weet wel wat bijvoorbeeld de fourieranalyse is, hoe hij werkt en wat hij doet.
Nee, ze bedoelen een taylorreeks met oneindig veel termen.quote:Op vrijdag 25 december 2009 17:03 schreef minibeer het volgende:
[..]
Gewoon de afgeleide dus? Sorry als dit geen nut heeft, maar ik heb binnenkort toch een toets over differentieren en integreeren.
vreemdquote:Op vrijdag 25 december 2009 16:14 schreef BasementDweller het volgende:
In mijn lial diktaat staat het volgende:
Stel v=(v1, v2, ... , vn)t. We definiëren v* als de complex geconjugeerde van v. Dan geldt v*tv= (v1² + ... + vn²).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik begrijp het niet helemaal. Bedoelen ze dat een integraaltransformatie de afgeleide van de integraal van <een functie maal nog iets> is? Dan is het me namelijk wel geheel duidelijk.quote:Op vrijdag 25 december 2009 17:14 schreef GlowMouse het volgende:
Een fouriertransformatie is een integraaltransformatie, maar er zijn er meerdere. http://nl.wikipedia.org/wiki/Integraaltransformatie is vrij duidelijk wat dat betreft.
Sorry :Squote:Op vrijdag 25 december 2009 17:14 schreef GlowMouse het volgende:
Nee, ze bedoelen een taylorreeks met oneindig veel termen.
Finally, someone let me out of my cage


Ik voel me echt dom, maar wat moet er gebeuren wanneer er dit staat (factor):
Ik heb het nog nooit gehad, en kom het nu opeens tegen in mijn wiskundeboek.
[ Bericht 1% gewijzigd door AE86_Trueno op 27-12-2009 13:00:17 ]
Ik heb het nog nooit gehad, en kom het nu opeens tegen in mijn wiskundeboek.
[ Bericht 1% gewijzigd door AE86_Trueno op 27-12-2009 13:00:17 ]


http://nl.wikipedia.org/wiki/Combinatie_%28wiskunde%29quote:Op zondag 27 december 2009 12:54 schreef AE86_Trueno het volgende:
Ik voel me echt dom, maar wat moet er gebeuren wanneer er dit staat:
[ afbeelding ]
Ik heb het nog nooit gehad, en kom het nu opeens tegen in mijn wiskundeboek.


Dankjewel, ik had het al wel ooit gehad. Was het alleen vergetenquote:Op zondag 27 december 2009 13:00 schreef BasementDweller het volgende:
[..]
http://nl.wikipedia.org/wiki/Combinatie_%28wiskunde%29


Geen probleem.
Zelf heb ik ook een vraagje.
De opgave is: bereken de limiet als (x,y,z)->(0,0,0) van sin(xyz)/xyz.
Ik dacht dat je dan gewoon xyz kon substitueren door t. Dan krijg je lim van t->0 sin(t)/t. Met de regel van L'Hôpital blijkt dat 1 te zijn. Het antwoord is echter 0... dus waarom is mijn antwoord fout en hoe kan je het wel doen?
Zelf heb ik ook een vraagje.
De opgave is: bereken de limiet als (x,y,z)->(0,0,0) van sin(xyz)/xyz.
Ik dacht dat je dan gewoon xyz kon substitueren door t. Dan krijg je lim van t->0 sin(t)/t. Met de regel van L'Hôpital blijkt dat 1 te zijn. Het antwoord is echter 0... dus waarom is mijn antwoord fout en hoe kan je het wel doen?


Inderdaad.... is het antwoord in het boek weer eens foutquote:
Is mijn argumentatie correct? Mag je dat xyz=t gebruiken?


de regel van L'Hôpital heb je trouwens niet nodig, je kunt ook de definitie van de afgeleide pakken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Nog een vraagje jonges.
Ik zit weer in de problemen met die faculteiten. Ik irriteer me er mateloos aan. Dus kan iemand me zeggen wat ik fout doe als ik zeg dat:
Ik (2n+2)! ook zou kunnen schrijven als: (2n+2)(2n+1)n!
Ik (2n)! ook zou kunnen shrijven als: (2n)n!
Daar ergens moet mijn fout zitten.
Ik zit weer in de problemen met die faculteiten. Ik irriteer me er mateloos aan. Dus kan iemand me zeggen wat ik fout doe als ik zeg dat:
Ik (2n+2)! ook zou kunnen schrijven als: (2n+2)(2n+1)n!
Ik (2n)! ook zou kunnen shrijven als: (2n)n!
Daar ergens moet mijn fout zitten.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Ik (2n)! ook zou kunnen shrijven als: (2n)n!
pak n=3, links staat 6!, ofwel 6*5*4*3*2*1
rechts staat 6*3!, ofwel 6*3*2*1.
Bij (2n+2)! ook zou kunnen schrijven als: (2n+2)(2n+1)n! kun je zo ook laten zien dat het fout is.
pak n=3, links staat 6!, ofwel 6*5*4*3*2*1
rechts staat 6*3!, ofwel 6*3*2*1.
Bij (2n+2)! ook zou kunnen schrijven als: (2n+2)(2n+1)n! kun je zo ook laten zien dat het fout is.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Nee, (2n + 2)! = (2n + 2)·(2n + 1)·(2n)!.
Neem anders een paar concrete gevallen om het idee te krijgen. n = 3, dan (2n + 2)! = 8! = 8·7·6·5·4·3·2·1 = 8·7·6! bijvoorbeeld, maar natuurlijk niet 8·7·3! wat jij zegt.
Neem anders een paar concrete gevallen om het idee te krijgen. n = 3, dan (2n + 2)! = 8! = 8·7·6·5·4·3·2·1 = 8·7·6! bijvoorbeeld, maar natuurlijk niet 8·7·3! wat jij zegt.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.