SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Lukt dat niet makkelijk met De Moivre?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


is dat niet iets met e^iy = cos x nog wat?quote:Op dinsdag 20 oktober 2009 20:27 schreef GlowMouse het volgende:
Lukt dat niet makkelijk met Euler?
Was voor je edit:
Even kijken naar Moivre
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Nou ik kom er echt niet uit:
Ik blijf steken bij:
Eerst schrijf ik de bovenste term naar polaire vorm:
r = ((-1)^2 + 1^2) = wortel(2)
z = wortel(2) (cos pi/4 + i sin pi/4 )
-1/wortel(2) + i/wortel(2) --> ((wortel(2)/wortel(2) (cos(pi/4) + i sin(pi/4) )^1001
--> 1 * ( cos(1001pi/4) + i sin (1001pi/4) )
---> aangezien 2pi een rondje is. 1000/2 = 500. Hou je 1 pi over?? Dus dan:
---> ( cos(5pi/4) + i sin (5 pi/4) ) en daarna raakt het een beetje in de soep.
Ik blijf steken bij:
Eerst schrijf ik de bovenste term naar polaire vorm:
r = ((-1)^2 + 1^2) = wortel(2)
z = wortel(2) (cos pi/4 + i sin pi/4 )
-1/wortel(2) + i/wortel(2) --> ((wortel(2)/wortel(2) (cos(pi/4) + i sin(pi/4) )^1001
--> 1 * ( cos(1001pi/4) + i sin (1001pi/4) )
---> aangezien 2pi een rondje is. 1000/2 = 500. Hou je 1 pi over?? Dus dan:
---> ( cos(5pi/4) + i sin (5 pi/4) ) en daarna raakt het een beetje in de soep.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Welk getal doe je nou? Want r=1 voor beide getallen.
En de hoek bij -1 + i is niet pi/4.
En de hoek bij -1 + i is niet pi/4.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


r = 1??? ehh... ik pak zeg maar -1 + 1*i voor de bovenste term.....quote:Op dinsdag 20 oktober 2009 21:09 schreef GlowMouse het volgende:
Welk getal doe je nou? Want r=1 voor beide getallen.
En de hoek bij -1 + i is niet pi/4.
Edit: en die hoek is natuurlijk 3/4 pi.
Maar als ik naar polaire vorm schrijf, dan wordt die -1+1i toch z = wortel ( 1 +1 ) ??
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


quote:Op dinsdag 20 oktober 2009 21:30 schreef GlowMouse het volgende:
waar komt -1+i vandaan dan?
van die boventerm : ( -1/wortel2 + i 1/wortel 2 )
In het boek zag ik dat ze hetzelfde doen met : 1/2 + 1/2 i gebruikten ze 1+i .. dus vandaar..
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Het is toch makkelijker om -1/wortel2 + i 1/wortel 2 te schrijven als cos(3pi/4) + i sin(3pi/4)?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


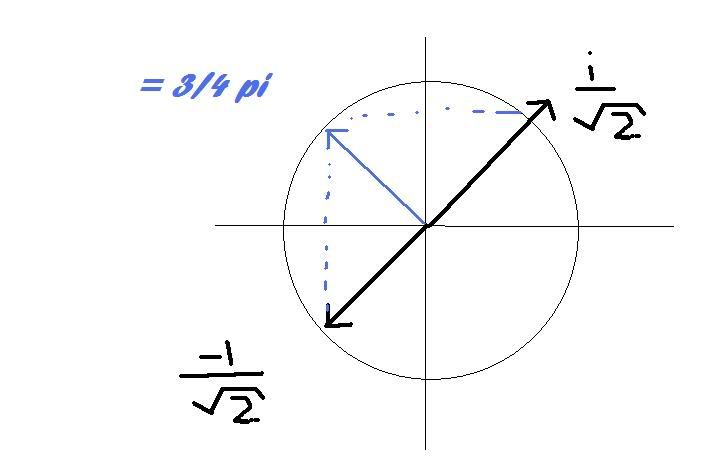
ff denken.... -1 wortel 2 = 5/4 pi + pi 1/4 --> ja idd dat wordt op de éénheidscirkel 3/4 pi. Ik ga even een paint maken om het te verduidelijken. kijken of ik het goed doe.quote:Op dinsdag 20 oktober 2009 21:42 schreef GlowMouse het volgende:
Het is toch makkelijker om -1/wortel2 + i 1/wortel 2 te schrijven als cos(3pi/4) + i sin(3pi/4)?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Schrijf eens de breuk als 1 e-macht, zoiets als et/en = et-n, en kijk wat de rest wordt als je de resulterende exponent modulo 2pi neemt.quote:Op dinsdag 20 oktober 2009 20:22 schreef Burakius het volgende:
Heey genialen,
Vrienden en ik kwamen niet uit deze som. (uitwerking is perongeluk boven i.p.v. beneden). Hoe kom je nou op die onderste term ^3( dus welk truukje wordt er nou uitgehaald bij de eerste bewerking). Help ons uit de brand.
[ afbeelding ]


btw. Even mijn totale noob plaatje:
Het is echt lang geleden, ik moet me maar eens totaal inlezen.
Het is echt lang geleden, ik moet me maar eens totaal inlezen.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


i / wortel2 ligt op de 'y-as' en -1/wortel2 ligt op de x-as
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Goed, het nemen van machten staat gelijk aan het doorcirkelen van dat ding op de eenheidsschijf. De vierde macht van dat ding is daarbij duidelijk 1. De 1000ste macht is dan ook 1, aangezien 1000 een veelvoud van 4 is. De 1001ste macht is dus gelijk aan het getal zelf.quote:Op dinsdag 20 oktober 2009 21:52 schreef Burakius het volgende:
btw. Even mijn totale noob plaatje:
[ afbeelding ]
Het is echt lang geleden, ik moet me maar eens totaal inlezen.


Ik begrijp het niet helemaal. De vierde macht van zowel cos ¾π + i∙sin ¾π als cos(-¼π) + i∙sin(-¼π) is -1, dus je kunt de machten van zowel teller als noemer mod 8 nemen. Niet dat daardoor iets verandert aan de uitwerking natuurlijk.quote:Op dinsdag 20 oktober 2009 22:08 schreef thabit het volgende:
[..]
Goed, het nemen van machten staat gelijk aan het doorcirkelen van dat ding op de eenheidsschijf. De vierde macht van dat ding is daarbij duidelijk 1. De 1000ste macht is dan ook 1, aangezien 1000 een veelvoud van 4 is. De 1001ste macht is dus gelijk aan het getal zelf.


Bij dit soort sommen schrijf ik altijd de zaak even om naar exponenten. In het meest algemene geval heb je iets alsquote:Op dinsdag 20 oktober 2009 20:22 schreef Burakius het volgende:
Heey genialen,
Vrienden en ik kwamen niet uit deze som. (uitwerking is perongeluk boven i.p.v. beneden). Hoe kom je nou op die onderste term ^3( dus welk truukje wordt er nou uitgehaald bij de eerste bewerking). Help ons uit de brand.
[ afbeelding ]
(a+bi)n
Nu ga je (a+bi) omschrijven in de vorm (a+bi)=reix, want dan kun je makkelijk uitrekenen dat
(a+bi)n = (reix)n = rneinx
In het algemeen geldt (teken het plaatje maar) dat
r = [a2+b2]1/2
en
tan(x) = b/a --> b/a=tan-1(x)
Hieruit kun je x en r oplossen in termen van a en b. Vervolgens schrijf je
rneinx
op. Dit doe je met de teller, en hetzelfde doe je met de noemer, en wat je overhoudt is een uitdrukking in de vorm
rneinx/[smeimx] = [rn/sm]ei(n-m)x.
Maar je kunt natuurlijk ook de plaatjes tekenen zoals werd aangegeven
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Okee, ja, vergissinkje.quote:Op woensdag 21 oktober 2009 00:22 schreef Riparius het volgende:
[..]
Ik begrijp het niet helemaal. De vierde macht van zowel cos ¾π + i∙sin ¾π als cos(-¼π) + i∙sin(-¼π) is -1, dus je kunt de machten van zowel teller als noemer mod 8 nemen. Niet dat daardoor iets verandert aan de uitwerking natuurlijk.


quote:
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Is dit toegestaan:
(1) (- 1/wortel(2) + i/wortel(2)) herschrijven tot 1/wortel(2) ( -1 + i ) ?
(2) modulus is wortel(2) en danzou het argument tan 1 zijn en dat is pi/4 , en dan klap ik het natuurlijk om door die -1 en dan wordt het 3/4 pi.
correct?
(1) (- 1/wortel(2) + i/wortel(2)) herschrijven tot 1/wortel(2) ( -1 + i ) ?
(2) modulus is wortel(2) en danzou het argument tan 1 zijn en dat is pi/4 , en dan klap ik het natuurlijk om door die -1 en dan wordt het 3/4 pi.
correct?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


1 ja
2 tan(x) = -1 dus x=3/4 pi (of x=-pi/4 maar die is het niet), niks 'klap ik het natuurlijk om', gewoon in 1x goed doen
2 tan(x) = -1 dus x=3/4 pi (of x=-pi/4 maar die is het niet), niks 'klap ik het natuurlijk om', gewoon in 1x goed doen
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dat is correct, maar ik zou beginnen om wortels in de noemer weg te werken. Je hebt immers:quote:Op woensdag 21 oktober 2009 18:52 schreef Burakius het volgende:
Is dit toegestaan:
(1) (- 1/wortel(2) + i/wortel(2)) herschrijven tot 1/wortel(2) ( -1 + i ) ?
1/√2 = ½√2
Lijkt me op zijn minst onnodig verwarrend om het zo te doen. Je moet het gewoon even visualiseren in het complexe vlak. Het beeldpunt van -1 + i ligt in het tweede kwadrant, dan zie je meteen dat het argument ¾π (mod 2π) is.quote:(2) modulus is wortel(2) en danzou het argument tan 1 zijn en dat is pi/4 , en dan klap ik het natuurlijk om door die -1 en dan wordt het 3/4 pi.
correct?


Ja maar ik schrijf het eerst om naar een driehoek met a= 1 b = 1 en r = wortel(2).
Want ik heb dus een tabel tot mijn beschikking die ik uit mijn hoofd ken. Daarin komt tan-1 niet voor, mar bij tan 1 weet ik wel dat het pi/4 is. En dan "klap ik het om" .
Want ik heb dus een tabel tot mijn beschikking die ik uit mijn hoofd ken. Daarin komt tan-1 niet voor, mar bij tan 1 weet ik wel dat het pi/4 is. En dan "klap ik het om" .
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Ja bij deze wel, maar bij pi/6 en pi/3 etc. vind ik het al moeilijker om te zien. Het liefst doe ik het dan op de langzame officiele wijze. Maar in een geval van pi/4 zou ik het wel zien natuurlijk. pi/2 trouwens ook.quote:Op woensdag 21 oktober 2009 19:15 schreef Riparius het volgende:
[..]
Dat is correct, maar ik zou beginnen om wortels in de noemer weg te werken. Je hebt immers:
1/√2 = ½√2
[..]
Lijkt me op zijn minst onnodig verwarrend om het zo te doen. Je moet het gewoon even visualiseren in het complexe vlak. Het beeldpunt van -1 + i ligt in het tweede kwadrant, dan zie je meteen dat het argument ¾π (mod 2π) is.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Tja, het is natuurlijk ook niet goed dat pi de verhouding tussen de omtrek en de middellijn van een cirkel aanduidt, in plaats van de verhouding tussen omtrek en straal. Het is op de een of andere manier historisch zo gegroeid natuurlijk, maar handig is anders omdat je je heel makkelijk in factoren 2 vergist. Maar goed, zo zijn er wel meer voorbeelden van slechte notatie te vinden die we toch nog dagelijks blijven gebruiken.quote:


Leg ees beter uit thabit  . Ik kom nog wel eens in de war met dat rad gedoe. Ik haat het.
. Ik kom nog wel eens in de war met dat rad gedoe. Ik haat het.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


In de meeste formules en stellingen waar pi in voorkomt, komt eigenlijk 2*pi voor. Zo is de omtrek van de eenheidscirkel gelijk aan 2*pi. En als gevolg daarvan de periode van de sinus en cosinus gelijk aan 2*pi. Als je een hoek van pi hebt gemaakt dan ben je nog maar halverwege het hele rondje, etc.


Oke jongens nog eentje.Deze is wat simpeler.
Nou snap ik de notatie van de domein(en?) niet helemaal. Maar wat ik iig wel kan is: (als hij dus invers is) is natuurlijk:
f(x)=sin x ---> y=sinx ---> arcsiny=x -----> arcsinx= y is de inverse.
MAAarr... daarna komt het antwoord met arcsin(x + pi ) . En dat zal wel te maken hebben met die domein(en). Kan het even niet zien.
p.s.
wij hanteren het domein pi tot -pi ... als dat hiermee te maken heeft
Nou snap ik de notatie van de domein(en?) niet helemaal. Maar wat ik iig wel kan is: (als hij dus invers is) is natuurlijk:
f(x)=sin x ---> y=sinx ---> arcsiny=x -----> arcsinx= y is de inverse.
MAAarr... daarna komt het antwoord met arcsin(x + pi ) . En dat zal wel te maken hebben met die domein(en). Kan het even niet zien.
p.s.
wij hanteren het domein pi tot -pi ... als dat hiermee te maken heeft
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Het oudst bekende gebruik van de letter π in de 'moderne' betekenis komt voor bij William Jones, Synopsis palmariorum matheseos (London, 1706) p. 263, maar de notatie lijkt mede te zijn geïnspireerd door het gebruik van de letters π en δ voor respectievelijk de omtrek (periferie) en diameter van een cirkel bij Oughtred, Clauis mathematicae (1652) p. 66. De notatie π voor de verhouding van de omtrek tot de middellijn van een cirkel is populair geworden doordat Euler deze consequent gebruikte in zijn invloedrijke Introductio in analysin inifinitorum (1748). Opmerkelijk is echter dat Euler in een brief aan d'Alembert gedateerd 15 april 1747 schrijft: soit π la circonférence d'un cercle dont le rayon = 1, en daarmee definieert hij π dan weer op de manier die jij graag zou willen, wat wel opmerkelijk mag heten omdat Euler het manuscript voor de Introductio al medio 1745 had voltooid.quote:Op woensdag 21 oktober 2009 19:54 schreef thabit het volgende:
In de meeste formules en stellingen waar pi in voorkomt, komt eigenlijk 2*pi voor. Zo is de omtrek van de eenheidscirkel gelijk aan 2*pi. En als gevolg daarvan de periode van de sinus en cosinus gelijk aan 2*pi. Als je een hoek van pi hebt gemaakt dan ben je nog maar halverwege het hele rondje, etc.
[ Bericht 0% gewijzigd door Riparius op 21-10-2009 21:04:32 ]


Heb je sin(x) al getekend van π/2 tot 3/2π?quote:Op woensdag 21 oktober 2009 20:46 schreef Burakius het volgende:
Oke jongens nog eentje.Deze is wat simpeler.
[ afbeelding ]
Nou snap ik de notatie van de domein(en?) niet helemaal. Maar wat ik iig wel kan is: (als hij dus invers is) is natuurlijk:
f(x)=sin x ---> y=sinx ---> arcsiny=x -----> arcsinx= y is de inverse.
MAAarr... daarna komt het antwoord met arcsin(x + pi ) . En dat zal wel te maken hebben met die domein(en). Kan het even niet zien.
p.s.
wij hanteren het domein pi tot -pi ... als dat hiermee te maken heeft
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik weet niet wie die vraag heeft gemaakt, maar geen van de vier gegeven antwoorden is juist als je althans de gangbare definitie van arcsin x hanteert.quote:Op woensdag 21 oktober 2009 20:46 schreef Burakius het volgende:
Oke jongens nog eentje.Deze is wat simpeler.
[ afbeelding ]
Nou snap ik de notatie van de domein(en?) niet helemaal. Maar wat ik iig wel kan is: (als hij dus invers is) is natuurlijk:
f(x)=sin x ---> y=sinx ---> arcsiny=x -----> arcsinx= y is de inverse.
MAAarr... daarna komt het antwoord met arcsin(x + pi ) . En dat zal wel te maken hebben met die domein(en). Kan het even niet zien.
p.s.
wij hanteren het domein pi tot -pi ... als dat hiermee te maken heeft