Er is binnen de Natuurkunde een formule opgesteld die de basis is van de beschrijjving van de gravitatie- kracht tussen 2 massas (M1 en M2) met onderlinge afstand r.
F = Constante * (M1 * M2) /(r *r )
Nu heb ik mijn kritiek t.a.v. de juistheid van deze formule; n.l. in die zin dat niet de massa causale veroorzaker is van deze kracht, maar wel de elektromagnetische en andere eigenschappen (die nader te onderzoeken zijn) binnen en om die betreffende massa(s).
Een leuk topic voor degene die vierkant achter de gravitatie-theorie staan en leuk voor critici, dacht ik zo.
Mijn stelling/issue om te openen:
Hoe kan men zich zo zeker voelen om direct de massa van de Aarde uit deze formule te berekenen op zo'n smalle basis ?
quote:is dat niet.in die zin dat niet de massa causale veroorzaker is van deze kracht, maar wel de elektromagnetische en andere eigenschappen (die nader te onderzoeken zijn) binnen en om die betreffende massa(s).
quote:Weet jij hoeveel experimenten uitgevoerd zijn die steeds weer dezelfde formule ondersteunden en geen één experiment dat het tegensprak? (rekening houdend met andere bekende effecten als elektrische aantrekking ed.).Hoe kan men zich zo zeker voelen om direct de massa van de Aarde uit deze formule te berekenen op zo'n smalle basis ?
De theorie stelt ook helemaal niet dat gravitatie causaal veroorzaakt wordt door massa maar stelt dat deze er aan gerelateerd is volgens de formule die jij plaatst.
quote:Weet ik, experiment kan volkomen in lijn zijn met de veronderstelde formule, desalniettemin kan de formule nog steeds ongefundeerd zijn w.b.t. aannames.Op dinsdag 7 juli 2009 20:03 schreef Barbaaf het volgende:
Doorgaans levert men, als men een wetenschappelijke theorie bekritiseert, argumenten en ondersteunend bewijs voor een alternatieve theorie.
[..]
is dat niet.
[..]
Weet jij hoeveel experimenten uitgevoerd zijn die steeds weer dezelfde formule ondersteunden en geen één experiment dat het tegensprak? (rekening houdend met andere bekende effecten als elektrische aantrekking ed.).
quote:de wetenschappelijke veronderstelling is toch dat primair die 2 massas elkaar aantrekken ?De theorie stelt ook helemaal niet dat gravitatie causaal veroorzaakt wordt door massa maar stelt dat deze er aan gerelateerd is volgens de formule die jij plaatst.
quote:(zie topic over wetenschappers die natuurkundewet breken).
Er zit een cirkelredenering in; Eerst komt de vastgestelde formule, daarna komt pas de berekende massa van de Aarde.
Als er een andere methode is/zou zijn om de massa van de Aarde vast te stellen, dan kan de gehele gravitatie-formule op basis van een andere ingang worden getoetst.
quote:maar de aannames bij die formule wel.Op dinsdag 7 juli 2009 20:27 schreef ..-._---_-.- het volgende:
Die formule zegt helemaal niets over causaliteit.
quote:Welke aannames? Noem ze eens?Op dinsdag 7 juli 2009 20:28 schreef Bankfurt het volgende:
[..]
maar de aannames bij die formule wel.
Dat lijkt me verder overigens helemaal niet relevant, aangezien je kritiek de formule betreft en niet de aannames:
quote:Nu heb ik mijn kritiek t.a.v. de juistheid van deze formule
[ Bericht 10% gewijzigd door #ANONIEM op 07-07-2009 20:30:45 ]
quote:Dan voeg ik ze er hierbij in.Op dinsdag 7 juli 2009 20:28 schreef ..-._---_-.- het volgende:
[..]
Welke aannames? Noem ze eens?
Dat lijkt me verder overigens helemaal niet relevant, aangezien je kritiek de formule betreft en niet de aannames:
[..]
quote:Dat lijkt me niet. Je kan G bepalen door naar de aantrekkingskracht te kijken die twee massieve objecten op elkaar uitoefenen. Daar heb je de massa van de aarde niet bij nodig.Op dinsdag 7 juli 2009 20:24 schreef Bankfurt het volgende:
[..]
(zie topic over wetenschappers die natuurkundewet breken).
Er zit een cirkelredenering in; Eerst komt de vastgestelde formule, daarna komt pas de berekende massa van de Aarde.
Als er een andere methode is/zou zijn om de massa van de Aarde vast te stellen, dan kan de gehele gravitatie-formule op basis van een andere ingang worden getoetst.
quote:uit dat topic:Op dinsdag 7 juli 2009 20:24 schreef Bankfurt het volgende:
[..]
(zie topic over wetenschappers die natuurkundewet breken).
Er zit een cirkelredenering in; Eerst komt de vastgestelde formule, daarna komt pas de berekende massa van de Aarde.
Als er een andere methode is/zou zijn om de massa van de Aarde vast te stellen, dan kan de gehele gravitatie-formule op basis van een andere ingang worden getoetst.
quote:Dat is de essentie van wetenschap: als een wet niet meer geldt doordat een experiment dit tegenspreekt, dan moet een nieuwe wet opgesteld worden die:Dr Tony Roberts and PhD student Christophe P. Haynes, from the School of Maths and Physics, showed the fractal-Einstein and Alexander-Orbach laws can fail in some instances, and have derived a new law to replace them.
a. alle voorgaande experimenten ondersteunt die ook door de oude wet ondersteund werden
b. alle nieuwe data ook verklaart en
c. de opening biedt om nieuwe experimenten te doen
En de cirkelredenering bestaat in jouw gedachten, de werkelijke redenering gaat meer als:
Waarneming: de aarde draait om de zon, de maan draait om de aarde en een hoop hemellichamen draaien ook om elkaar.
Vraag: hoe kan dat?
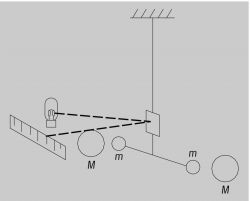
Touwen ertussen zijn nooit aangetroffen en het idee van een grote onzichtbare hand is ook niet erg wetenschappelijk, maar iemand dacht dat ze elkaar misschien gewoon aantrekken door er te zijn. Niemand geloofde dat natuurlijk maar hij bouwde zo'n toestel als hierboven en verdomd, voorwerpen bleken elkaar aan te trekken. Zelfs cynici, die goochelarij vermoeden konden zo'n simpel apparaat nabouwen en die bleken ook te werken. Sterker nog, als men de kracht ging meten bleek deze aan een constante formule te voldoen.
Waar de zwaartekracht vandaan komt weet men volgens mij nog niet (helemaal) maar daar gaat de wet ook niet over, die stelt alleen dat er een verband is tussen massa en aantrekking. Geen experiment dat het tegenspreekt, dus waarom niet die formule te gebruiken om de massa van planeten te berekenen? De berekende massa's komen doorgaans ook aardig overeen met wat men verwacht van die planeten, dus geen enkele reden aan de geldigheid van de formule te twijfelen.
quote:Op dinsdag 7 juli 2009 11:52 schreef Bankfurt het volgende:
[..]
Ja, ik heb een bron, ik ga hem niet geven want dan wordt die bron verboden.
Je kunt direct het internet afstruinen naar Newton, maar of je het dan zult vinden, betwijffel ik.
quote:Ja, dit verhaal is precies wat ik bedoel; ijzersterke samenvatting van mijn probleem.Op dinsdag 7 juli 2009 20:43 schreef Barbaaf het volgende:
[..]
uit dat topic:
[..]
Dat is de essentie van wetenschap: als een wet niet meer geldt doordat een experiment dit tegenspreekt, dan moet een nieuwe wet opgesteld worden die:
a. alle voorgaande experimenten ondersteunt die ook door de oude wet ondersteund werden
b. alle nieuwe data ook verklaart en
c. de opening biedt om nieuwe experimenten te doen
En de cirkelredenering bestaat in jouw gedachten, de werkelijke redenering gaat meer als:
Waarneming: de aarde draait om de zon, de maan draait om de aarde en een hoop hemellichamen draaien ook om elkaar.
Vraag: hoe kan dat?
Touwen ertussen zijn nooit aangetroffen en het idee van een grote onzichtbare hand is ook niet erg wetenschappelijk, maar iemand dacht dat ze elkaar misschien gewoon aantrekken door er te zijn. Niemand geloofde dat natuurlijk maar hij bouwde zo'n toestel als hierboven en verdomd, voorwerpen bleken elkaar aan te trekken. Zelfs cynici, die goochelarij vermoeden konden zo'n simpel apparaat nabouwen en die bleken ook te werken. Sterker nog, als men de kracht ging meten bleek deze aan een constante formule te voldoen.
Waar de zwaartekracht vandaan komt weet men volgens mij nog niet (helemaal) maar daar gaat de wet ook niet over, die stelt alleen dat er een verband is tussen massa en aantrekking. Geen experiment dat het tegenspreekt, dus waarom niet die formule te gebruiken om de massa van planeten te berekenen? De berekende massa's komen doorgaans ook aardig overeen met wat men verwacht van die planeten, dus geen enkele reden aan de geldigheid van de formule te twijfelen.
Juist deze snelle besliissing om dan maar gelijk te veronderstellen dat DAAROM de gravitatiewet/formule juist is, is naar mijn mening veel te kort door de bocht en VERKLAART .... niet noodzakelijkerwijs de gravitatiekracht (of hoe die kracht dan ook genoemd moet worden) die juist weer wel (en vaak zeer consistent) gemeten wordt.
P.s. ik ben geen trol, en ik heb dit topic juist geopend omdat ik anders met dit topic alleen in dat onzinnige TRU of BNW terecht zou komen, volgens de moderators. vandaar. Dit bewijst al weer hoe gevoelig dit onderwerp is. En het sterkt mij des te meer om de bron niet te noemen.
quote:Nee tuurlijk verklaart die formule zwaartekracht niet.... Hij beschrijft/modelleert de effecten. Dat is iets heel anders.Op dinsdag 7 juli 2009 20:51 schreef Bankfurt het volgende:
[..]
Ja, dit verhaal is precies wat ik bedoel; ijzersterke samenvatting van mijn probleem.
Juist deze snelle besliissing om dan maar gelijk te veronderstellen dat DAAROM de gravitatiewet/formule juist is, is naar mijn mening veel te kort door de bocht en VERKLAART .... niet noodzakelijkerwijs de gravitatiekracht (of hoe die kracht dan ook genoemd moet worden) die juist weer wel (en vaak zeer consistent) gemeten wordt.
P.s. ik ben geen trol, en ik heb dit topic juist geopend omdat ik anders met dit topic alleen in dat onzinnige TRU of BNW terecht zou komen, volgens de moderators. vandaar. Dit bewijst al weer hoe gevoelig dit onderwerp is. En het sterkt mij des te meer om de bron niet te noemen.
quote:idd. Niet meer dan dat. We zijn het eens.Op dinsdag 7 juli 2009 20:56 schreef ATuin-hek het volgende:
[..]
Nee tuurlijk verklaart die formule zwaartekracht niet.... Hij beschrijft/modelleert de effecten. Dat is iets heel anders.
quote:Als je een "betere" beschrijving van zwaartekracht wil hebben kun je es naar de algemene relativiteitstheorie kijken.Op dinsdag 7 juli 2009 21:01 schreef Bankfurt het volgende:
[..]
idd. Niet meer dan dat. We zijn het eens.
quote:Doe es niet zo sensationeelOp dinsdag 7 juli 2009 20:51 schreef Bankfurt het volgende:
P.s. ik ben geen trol, en ik heb dit topic juist geopend omdat ik anders met dit topic alleen in dat onzinnige TRU of BNW terecht zou komen, volgens de moderators. vandaar. Dit bewijst al weer hoe gevoelig dit onderwerp is. En het sterkt mij des te meer om de bron niet te noemen.
Zal es even opzoeken hoe men precies G bepaald heeft; ik kan me alleen een Cavendish-experiment herinneren, maar volgens mij was dat origineel bedoeld om de dichtheid van de aarde te bepalen.quote:G of g (op een zekere locatie) is heel makkelijk te bepalen/meten m.b.v. meten van vallende voorwerpen in een wrijvingsloze omgeving, ongeacht de massa van het vallende voorwerp.Op woensdag 8 juli 2009 12:51 schreef Haushofer het volgende:
[..]
Doe es niet zo sensationeel
2 dingen hoef je slechts te meten:
De hoogte van de val: h
De tijdsduur van de val: t
quote:Je hoeft niks op te zoeken, het is zo verschrikkelijk simpel.
quote:Wat een nietszeggend antwoord.Op woensdag 8 juli 2009 13:17 schreef Bankfurt het volgende:
[..]
Je hoeft niks op te zoeken, het is zo verschrikkelijk simpel.
quote:Kun je iets toevoegen dan ?
quote:Zit je nou expres te trollen of lijkt het maar zo? Haus vroeg iets aan jou. Dat was geen vraag waar ik antwoord op kan geven.
quote:Haushofer vroeg zich af hoe de gravitatieconstante G of g kon worden afgeleid en wilde dat opzoeken; en daar gaf ik direct antwoord op, omdat het zo simpel is. Daar wilde ik heen.Op woensdag 8 juli 2009 14:11 schreef ATuin-hek het volgende:
[..]
Zit je nou expres te trollen of lijkt het maar zo? Haus vroeg iets aan jou. Dat was geen vraag waar ik antwoord op kan geven.
quote:Als ik een massa op hoogte h naar beneden laat vallen, dan geldt ideaal dat h = 1/2 g*t2Op woensdag 8 juli 2009 13:06 schreef Bankfurt het volgende:
[..]
G of g (op een zekere locatie) is heel makkelijk te bepalen/meten m.b.v. meten van vallende voorwerpen in een wrijvingsloze omgeving, ongeacht de massa van het vallende voorwerp.
2 dingen hoef je slechts te meten:
De hoogte van de val: h
De tijdsduur van de val: t
(via ax=0, yx = g, vx=0, vy=g*t, x = 0, y=h=1/2*g*t2).
Dus:
g=2*h/t2
De kracht F op die massa m is gelijk aan F=m*g, en die kracht is natuurlijk ook gelijk aan F=G*M*m/r2 waarbij M de massa van de aarde is. Er geldt dus dat
G*M/r2=g
Hierbij is r de afstand tussen de massamiddelpunten van m en M.
En wat is nu je punt?
quote:Dit soort antwoorden zijn niet echt constructief, hé.Op woensdag 8 juli 2009 13:17 schreef Bankfurt het volgende:
[..]
Je hoeft niks op te zoeken, het is zo verschrikkelijk simpel.
quote:Zo bedoelde ik dat niet,Op woensdag 8 juli 2009 18:39 schreef Haushofer het volgende:
[..]
Dit soort antwoorden zijn niet echt constructief, hé.
jouw formules zijn idd waar het om gaat.
Nu is mijn punt dit: de formule kan wel bevredigende uitkomsten (op het 1e gezicht) geven, maar:
1e) zijn M1 en M2 daadwerkelijk de verklarende variabelen ?
Dit is bijna onmogelijk te toetsen binnen de gangbare wetenschappelijke etiquette.
2e) Wat als M een totaal andere waarde heeft, bijv. veel kleiner ? Dan hebben we een echt probleem met de gravitatietheorie.
Wat Newton deed, is eens bedenken hoe de werkelijkheid in elkaar zou zitten en daar een model voor maken. Bijvoorbeeld: Zolang er geen kracht op een bewegend voorwerp wordt uitgeoefend gaat het in een eenparige rechtlijnige beweging voort.
Kon Newton dat óóit testen? Nee. Het is natuurlijk een abstractie, een denkstap verder. Qua aantrekkingskracht tussen objecten kun je magnetisme, elektriciteit of zwaartekracht onderscheiden. Magnetisme is nog vrij gemakkelijk. Je kunt ook meten dat als je de objecten verder van elkaar af brengt dat de aantrekkingskracht ook afneemt. De formule zelf kun je niet uit de experimenten afleiden, maar je kunt die wel proberen te verifiëren.
Voor de zwaartekracht kun je dit ook doen. Maar het probleem is, de zwaartekracht is heel zwak. Maar je kunt twee grote massa's bij elkaar in de buurt leggen (ééntje veel groter dan de ander) en dan oefenen ze inderdaad een kracht op elkaar uit. Die kracht is te meten. Als je de massa's groter en kleiner maakt, of de afstand verandert, verandert de kracht ook.
Newtoniaans gezien blijkt inderdaad dat F = Constante * (M1 * M2) /(r2) een juiste beschrijving is. Verdubbel je de afstand, neemt de kracht met een factor vier af. Vergroot je de massa met een 10-voud, dan neemt de kracht ook met een 10-voud toe.
Dat is dus alleen verhoudingen. Zo kun je afleiden hóé de kracht precies in relatie staat tot M1, M2 en r. Echter, de gravitieconstante is er nog om de verhouding te kwantificeren (deels is die natuurlijk het gevolg van hoe wij onze eenheden hebben gekozen, een constante is op één te brengen door je eenheden te schalen).
Maar om even terug te komen, je kunt dus in principe experimenteel zien dat F = c(M1 x M2)/r2 moet gelden zonder te weten wat c is, maar alleen door te zien hoe F verandert als je M1, M2 of r verandert. Daar zit nog geen cirkelredenatie in.
Dan, als je dus aanneemt dat dit een valide model is, dan kun je natuurlijk G gaan bepalen. Dan, als je G nauwkeurig bepaald hebt, kun je ook de massa van de aarde bepalen.
[ Bericht 0% gewijzigd door Iblis op 08-07-2009 22:18:47 ]
quote:Ik begrijp nog steeds niet wat je punt nou is.Op woensdag 8 juli 2009 18:57 schreef Bankfurt het volgende:
[..]
Zo bedoelde ik dat niet,
jouw formules zijn idd waar het om gaat.
Nu is mijn punt dit: de formule kan wel bevredigende uitkomsten (op het 1e gezicht) geven, maar:
1e) zijn M1 en M2 daadwerkelijk de verklarende variabelen ?
Dit is bijna onmogelijk te toetsen binnen de gangbare wetenschappelijke etiquette.
2e) Wat als M een totaal andere waarde heeft, bijv. veel kleiner ? Dan hebben we een echt probleem met de gravitatietheorie.
Ja, misschien klopt Newton zijn theorie niet goed. Dat de theorie een benadering is, weten we al. Maar waarom kunnen we er dan zoveel zaken zo nauwkeurig mee beschrijven, ook in ons zonnestelsel of als het om grotere schalen gaat? Daar hoor ik je helemaal niet over. Bovendien heeft de algemene relativiteitstheorie Newton als klassieke limiet, en de ART is zeer nauwkeurig getoetst.
Wat bedoel je met "verklarende variabelen"? Massa is de "lading" waar zwaartekracht op inwerkt klassiek gezien; relativistisch gezien is dat energie in het algemeen.
Besef je overigens wel dat Newton's gravitatietheorie als status een benadering heeft in de natuurkunde?
quote:Als ik zijn punt begreep (in de andere topic) is het (mede) dat de formule vicieus opgesteld is. Om G te bepalen moet je de formule hebben, om de formule op te stellen moet je (in zijn ogen) G weten.
Ik begrijp nog steeds niet wat je punt nou is.
quote:Ah, maar dat laatste is niet waar.Op woensdag 8 juli 2009 22:09 schreef Iblis het volgende:
[..]
Als ik zijn punt begreep (in de andere topic) is het (mede) dat de formule vicieus opgesteld is. Om G te bepalen moet je de formule hebben, om de formule op te stellen moet je (in zijn ogen) G weten.
Newton redeneerde dat de zwaartekracht tussen 2 massa's evenredig is aan het product van die massa's, en omgekeerd evenredig met het kwadraat van de afstand tussen de massamiddelpunten. Dimensioneel komt er dan nog een constante voor je formule, en dat is G. De exacte waarde ervan bepaalt dan de sterkte van de zwaartekracht.
Die eenheid van G is trouwens al een intuïtieve indicatie dat zwaartekracht niet renormalizeerbaar is, maar dan ga je al weer in het regime van de kwantumveldentheorie en kwantumgravitatie.
-edit Wat jij zegt dus
[ Bericht 5% gewijzigd door Haushofer op 08-07-2009 22:23:41 ]
quote:G is wel even iets heel anders dan g he, vergeet dat niet.Op woensdag 8 juli 2009 16:01 schreef Bankfurt het volgende:
[..]
Haushofer vroeg zich af hoe de gravitatieconstante G of g kon worden afgeleid en wilde dat opzoeken; en daar gaf ik direct antwoord op, omdat het zo simpel is. Daar wilde ik heen.
quote:Nogmaals, er wordt niets verklaard. Er wordt beschreven. Als jij je kritiek baseert op het niet willen begrijpen wat er precies gesteld wordt schiet het niet op hè?Op woensdag 8 juli 2009 18:57 schreef Bankfurt het volgende:
[..]
Zo bedoelde ik dat niet,
jouw formules zijn idd waar het om gaat.
Nu is mijn punt dit: de formule kan wel bevredigende uitkomsten (op het 1e gezicht) geven, maar:
1e) zijn M1 en M2 daadwerkelijk de verklarende variabelen ?
quote:Oh? Welk probleem? Tenzij je op moleculair niveau gaat kijken misschien. En kom niet aan met "dat heb ik ergens gelezen maar ik vertel niet waar want dan wordt die website gesloten".Dit is bijna onmogelijk te toetsen binnen de gangbare wetenschappelijke etiquette.
2e) Wat als M een totaal andere waarde heeft, bijv. veel kleiner ? Dan hebben we een echt probleem met de gravitatietheorie.
quote:De theorie is niet van Netwon zelf, maar van zijn volgelingen-critici.Op woensdag 8 juli 2009 22:07 schreef Haushofer het volgende:
[..]
Ik begrijp nog steeds niet wat je punt nou is.
Ja, misschien klopt Newton zijn theorie niet goed. Dat de theorie een benadering is, weten we al. Maar waarom kunnen we er dan zoveel zaken zo nauwkeurig mee beschrijven, ook in ons zonnestelsel of als het om grotere schalen gaat? Daar hoor ik je helemaal niet over. Bovendien heeft de algemene relativiteitstheorie Newton als klassieke limiet, en de ART is zeer nauwkeurig getoetst.
g is niet contant, niet zo zeer in de zin van a.g.v. van kromming van de aarde, maar vooral meer wel dat de samenstelling van de aardeinhoud niet homogeen is (kom ik zo op terug), d.w.z. het zwaartepunt van de Aarde is niet zo mooi centraal liggend (althans volgens de formule, en uitgaande dat de formule nog steeds juist is)...
quote:verklarende variabelen hier suggereert dat de massa's (en zo wordt het ook verkocht in de eenvoudige Natuurkunde) een kracht uitstralen of een kracht genereren. D.w.z. verklaring van deze "mooie formule".Wat bedoel je met "verklarende variabelen"? Massa is de "lading" waar zwaartekracht op inwerkt klassiek gezien; relativistisch gezien is dat energie in het algemeen.
quote:Jawel.Besef je overigens wel dat Newton's gravitatietheorie als status een benadering heeft in de natuurkunde?
Het punt:
Het punt is nu dit, doordat men de massa heeft berekend van de Aarde (m.b.v. die formule), en het bekende gegeven van de INHOUD van de Aarde, stelt men dat (het zal dan wel moeten in die zin) de samenstelling van de innerlijke Aarde in de diepte steeds dichtere materie bevat (o.d.d. een kern van metaal, ijzer/nikkel etc).
Nu kom ik met de kwestie:
- Hoe kan dit binnenste nou een metaal (ijzer/nikkel) zijn ? Het lijkt mij dan dat het binnenste van de Aarde zo gloeiend heet is, dat het metaal wel vloeibaar moet zijn en door de draaiing van de Aarde naar buiten moet schieten/exploderen, wat echter niet gebeurt.
- Suggereert men dit (deze metalen kern) OMDAT men anders het Aarde-magnetisme dan NIET verklaren kan ?
Lezen: http://nl.wikipedia.org/wiki/Aardkern , hoe de dichtheid van de Aarde _ook_ bepaald is.
Denken: waarom worden de oceanen niet van de Aarde geslingerd?
quote:Misschien ben ik dom maar; g = de valversnelling en heeft niks te maken met de gravitatieconstante (G)..?Op vrijdag 10 juli 2009 19:40 schreef Bankfurt het volgende:
g is niet contant, niet zo zeer in de zin van a.g.v. van kromming van de aarde, maar vooral meer wel dat de samenstelling van de aardeinhoud niet homogeen is (kom ik zo op terug), d.w.z. het zwaartepunt van de Aarde is niet zo mooi centraal liggend (althans volgens de formule, en uitgaande dat de formule nog steeds juist is)...
quote:Ja, het lijkt me duidelijk dat het komt door massa, men heeft dit nogal uitvoerig getest met als enige variabele de massa (en afstand) om te zien wat de krachten waren die massa's op elkaar uitoefende. Hier hoef je geen complot achter te zoeken.verklarende variabelen hier suggereert dat de massa's (en zo wordt het ook verkocht in de eenvoudige Natuurkunde) een kracht uitstralen of een kracht genereren. D.w.z. verklaring van deze "mooie formule".
quote:Ik snap niet helemaal wat je hier bedoelt (draaiing van de aarde gedeelte), maar eh er schiet wel degelijk wat naar buiten, vulkanen maybe? Verder zitten er meerdere "mantels" om de vloeibare kern van de aarde, binnemantel, buitenmantel en ook nog de aardkorst. En die mantels zijn nogal dikHoe kan dit binnenste nou een metaal (ijzer/nikkel) zijn ? Het lijkt mij dan dat het binnenste van de Aarde zo gloeiend heet is, dat het metaal wel vloeibaar moet zijn en door de draaiing van de Aarde naar buiten moet schieten/exploderen, wat echter niet gebeurt.
En vergeet niet dat de aarde miljoenen jaren lang (of mag ik zelfs van miljarden spreken?) nogal "onrustig" was qua vulkanische activiteit 
quote:Geen idee.- Suggereert men dit (deze metalen kern) OMDAT men anders het Aarde-magnetisme dan NIET verklaren kan ?
quote:Voor zover ik het begrijp is zijn wantrouwen gebaseerd op onvolledige kennis en begrip van de natuurkunde en wetenschap in het algemeen en wordt deze verder gevoed door pseudo-wetenschappelijke bronnen.Op zaterdag 11 juli 2009 04:31 schreef ATuin-hek het volgende:
Oftewel, het wantrouwen van de TS is nergens op gebaseerd?
quote:Volgens mij is de primaire reden dat g niet constant is het feit dat de aarde draait en je dus aan de evenaar de grootste centrifugale kracht ervaart; zo uit m'n hoofd is g op de polen circa 9,83 m/s2 en op de evenaar 9,79 m/s2 oid.Op vrijdag 10 juli 2009 19:40 schreef Bankfurt het volgende:
[..]
De theorie is niet van Netwon zelf, maar van zijn volgelingen-critici.
g is niet contant, niet zo zeer in de zin van a.g.v. van kromming van de aarde, maar vooral meer wel dat de samenstelling van de aardeinhoud niet homogeen is (kom ik zo op terug), d.w.z. het zwaartepunt van de Aarde is niet zo mooi centraal liggend (althans volgens de formule, en uitgaande dat de formule nog steeds juist is)...
[..]
quote:Zwaartekracht werkt in op de ladingen massa, zoals het elektromagnetisme inwerkt op elektrische ladingen. Wat "eenvoudige natuurkunde" is, weet ik niet. Een echte verklaring voor zwaartekracht geeft die formule niet; die beschrijft alleen in een bepaalde limiet de zwaartekracht tussen 2 massa's. Maar we weten dat zwaartekracht niet instantaan werkt zoals de formule suggereert, en we weten ook dat zwaartekracht tussen energie in het algemeen werkt.verklarende variabelen hier suggereert dat de massa's (en zo wordt het ook verkocht in de eenvoudige Natuurkunde) een kracht uitstralen of een kracht genereren. D.w.z. verklaring van deze "mooie formule".
[..]
quote:Dat zou ik zo gauw niet weten, of men dat op die manier doet. Wat je ook kunt doen is natuurlijk op verschillende dieptes kijken wat de dichtheid is. In het simpele geval middel je die dichtheid, maar je zou eigenlijk een dichtheidsfunctie op moeten stellen om zo de totale massa uit te rekenen met een integraal.Jawel.
Het punt:
Het punt is nu dit, doordat men de massa heeft berekend van de Aarde (m.b.v. die formule), en het bekende gegeven van de INHOUD van de Aarde, stelt men dat (het zal dan wel moeten in die zin) de samenstelling van de innerlijke Aarde in de diepte steeds dichtere materie bevat (o.d.d. een kern van metaal, ijzer/nikkel etc).
quote:Waarom door de draaiing van de aarde?Nu kom ik met de kwestie:
- Hoe kan dit binnenste nou een metaal (ijzer/nikkel) zijn ? Het lijkt mij dan dat het binnenste van de Aarde zo gloeiend heet is, dat het metaal wel vloeibaar moet zijn en door de draaiing van de Aarde naar buiten moet schieten/exploderen, wat echter niet gebeurt.
quote:Ik ben hier niet zo thuis in, misschien dat iemand hier antwoord op heeft- Suggereert men dit (deze metalen kern) OMDAT men anders het Aarde-magnetisme dan NIET verklaren kan ?
Ik zal deze es doorlezen met eventuele bronnen 
quote:G is een constante, g is de zwaartekracht-versnelling idd op het Aarde-Oppervlak.Op zaterdag 11 juli 2009 10:55 schreef Diabox het volgende:
[..]
Ik snap niet helemaal wat je hier bedoelt (draaiing van de aarde gedeelte), maar eh er schiet wel degelijk wat naar buiten, vulkanen maybe? Verder zitten er meerdere "mantels" om de vloeibare kern van de aarde, binnemantel, buitenmantel en ook nog de aardkorst. En die mantels zijn nogal dik
[..]
Geen idee.
Dat verhaal van die mantels is mij bekend, maar speculatief in die zin, dat nog niet (voor zover ik weet niet) door de officiele wetenschap een fysieke expeditie naar het binnenste van de Aarde bekend is ondernomen en bekend is gemaakt. Om kort te zijn: Wie daadwerkelijk stelt dat het binnenste van de Aarde een bol is van nikkel/ijzer, moet dan maar eens met concrete bewijzen komen.
Waarom zou het binnenste van de Aarde bijvoorbeeld niet van wolfraam of goud kunnen zijn, of gasvormig , of misschien vacuum ?
N.b. Wikipedia vind ik geen serieuze wetenschappelijke bron an sich, hooguit als hulpniddel om naar serieuze bronnen zoals oudere en verificeerbare boeken en verslagen te verwijzen.
quote:speelt idd ook mee, maar als je kijkt naar positie (constant op breedtegraad), dan nog zijn er grote verschillen gemeten in g.Op zaterdag 11 juli 2009 14:49 schreef Haushofer het volgende:
[..]
Volgens mij is de primaire reden dat g niet constant is het feit dat de aarde draait en je dus aan de evenaar de grootste centrifugale kracht ervaart; zo uit m'n hoofd is g op de polen circa 9,83 m/s2 en op de evenaar 9,79 m/s2 oid.
[..]
quote:Dan weet je al heel veel meer dan de doorsnee natuurkundige.Zwaartekracht werkt in op de ladingen massa, zoals het elektromagnetisme inwerkt op elektrische ladingen. Wat "eenvoudige natuurkunde" is, weet ik niet. Een echte verklaring voor zwaartekracht geeft die formule niet; die beschrijft alleen in een bepaalde limiet de zwaartekracht tussen 2 massa's. Maar we weten dat zwaartekracht niet instantaan werkt zoals de formule suggereert, en we weten ook dat zwaartekracht tussen energie in het algemeen werkt.
[..]
quote:idd, kijk dat schiet al op.Dat zou ik zo gauw niet weten, of men dat op die manier doet. Wat je ook kunt doen is natuurlijk op verschillende dieptes kijken wat de dichtheid is. In het simpele geval middel je die dichtheid, maar je zou eigenlijk een dichtheidsfunctie op moeten stellen om zo de totale massa uit te rekenen met een integraal.
[..]
quote:Net zoals in een draaimolen, draaiende losse delen schieten/willen naar buiten en dit veroorzaakt een druk vanuit het centrum van de aarde naar de buitenste delen van de Aarde. Althans dat zou je toch mogen verwachten van zwaar vloeibaar metalen substantie dat ronddraait om de Aarde-kern.Waarom door de draaiing van de aarde?
[..]
quote:De Aarde heeft ook een magnetisch veld, en niet zo'n klein beetje ook, om dit veld te verklaren EN de veronderstelde relatieve grote zwaartte van de Aarde LIJKT het alsof de officiele wetenschap als laatste strohalm een metalen magnetische substantie "wenst" in het inwendige van de Aarde.(heel amusant)Ik ben hier niet zo thuis in, misschien dat iemand hier antwoord op heeft
quote:Heel simpel. Dat weten ze door naar golfgedrag te kijken. Uit snelheidsverschillen, reflecties, brekingen etc. kan je heel veel achterhalen over de samenstelling van een medium.Op zaterdag 11 juli 2009 21:48 schreef Bankfurt het volgende:
[..]
G is een constante, g is de zwaartekracht-versnelling idd op het Aarde-Oppervlak.
Dat verhaal van die mantels is mij bekend, maar speculatief in die zin, dat nog niet (voor zover ik weet niet) door de officiele wetenschap een fysieke expeditie naar het binnenste van de Aarde bekend is ondernomen en bekend is gemaakt. Om kort te zijn: Wie daadwerkelijk stelt dat het binnenste van de Aarde een bol is van nikkel/ijzer, moet dan maar eens met concrete bewijzen komen.
Waarom zou het binnenste van de Aarde bijvoorbeeld niet van wolfraam of goud kunnen zijn, of gasvormig , of misschien vacuum ?
N.b. Wikipedia vind ik geen serieuze wetenschappelijke bron an sich, hooguit als hulpniddel om naar serieuze bronnen zoals oudere en verificeerbare boeken en verslagen te verwijzen.
quote:Wat is dit voor flauwekul? Hoeveel "natuurkundigen" ken jij persoonlijk?Op zaterdag 11 juli 2009 22:00 schreef Bankfurt het volgende:
Dan weet je al heel veel meer dan de doorsnee natuurkundige.
[..]
quote:You're joking right?.... iedere 1ste jaars natuurkundige weet ditOp zaterdag 11 juli 2009 22:00 schreef Bankfurt het volgende:
[..]
Dan weet je al heel veel meer dan de doorsnee natuurkundige.
quote:Maar gelukkig weet jij het beter? Man, in iedere regel die je neerpent geef je meer en meer blijk echt de ballen verstand ervan te hebben, 't enige wat jij kan zeggen is "'t lijkt maar zo... ze zeggen dat 't zo is... etc." maar geen enkele keer kom je ook maar met een spatje bewijs op de proppen dat het anders zou zijn. Je eist nu ook dat er een expeditie naar de aardkern moet zijn voordat je de huidige theorie geloofwaardig vindt maar je komt zelf echt helemaal nergens mee.Op zaterdag 11 juli 2009 22:00 schreef Bankfurt het volgende:
De Aarde heeft ook een magnetisch veld, en niet zo'n klein beetje ook, om dit veld te verklaren EN de veronderstelde relatieve grote zwaartte van de Aarde LIJKT het alsof de officiele wetenschap als laatste strohalm een metalen magnetische substantie "wenst" in het inwendige van de Aarde.(heel amusant)
Ik stel voor dat er een slotje op dit topic komt totdat TS de eerste paar klassen van de middelbare school heeft doorlopen
quote:Doordat metaal zwaarder is dan steen kost het minder energie om steen naar buiten te slingeren dan metaal dus blijft het meeste metaal in de kern.Op zaterdag 11 juli 2009 22:00 schreef Bankfurt het volgende:
Net zoals in een draaimolen, draaiende losse delen schieten/willen naar buiten en dit veroorzaakt een druk vanuit het centrum van de aarde naar de buitenste delen van de Aarde. Althans dat zou je toch mogen verwachten van zwaar vloeibaar metalen substantie dat ronddraait om de Aarde-kern.
[..]
een deel van de kern is vast omdat de druk op die diepte te groot is om vloeibaar te kunnen zijn
quote:niet alle planeten hebben een magnetisch veld maar hebben wel invloed op de zwaartekracht.De Aarde heeft ook een magnetisch veld, en niet zo'n klein beetje ook, om dit veld te verklaren EN de veronderstelde relatieve grote zwaartte van de Aarde LIJKT het alsof de officiele wetenschap als laatste strohalm een metalen magnetische substantie "wenst" in het inwendige van de Aarde.(heel amusant)
quote:Wel verschillen, geen grote verschillen. Er is een theoretische vorm van de aarde, waar de zwaartekracht potentiaal precies gelijk is. Dat is de geoïde. Idealiter zou, als je b.v. buizen onder het land door zou boren, en het windstil was op oceanen, het water zich precies over die geoïde verdelen.
speelt idd ook mee, maar als je kijkt naar positie (constant op breedtegraad), dan nog zijn er grote verschillen gemeten in g.
Die geoïde is weliswaar glad van vorm, maar wel erg onregelmatig. Het simpelste model van de aarde is een bol, een iets verfijnder model is een ellipsoïde, maar de geoïde wijkt daar vanaf:
Hierboven zie je de vorm van de aarde en de ‘afwijkingen’ van de zwaartekracht zoals die gemeten zijn, dit zijn afwijkingen t.o.v. van de ellipsoïde. Een Gal is een versnelling van 1 cm/s2, dus een milligal 10 micrometer / s2. Dat is vrij weinig t.o.v. de 9.8m/s2 die aangehouden wordt.
quote:Jawel, maar na 10 jaar zijn ze alles toch weer vergeten.Op zondag 12 juli 2009 21:06 schreef Twpk het volgende:
[..]
You're joking right?.... iedere 1ste jaars natuurkundige weet dit
quote:En jij niet, natuurlijkOp maandag 13 juli 2009 11:18 schreef Bankfurt het volgende:
[..]
Jawel, maar na 10 jaar zijn ze alles toch weer vergeten.
Ik denk dat jij wat teveel pretenties hebt
quote:Mooie plaatjes, 1% afwijking vind ik al heel wat. Dat van die buizen vind ik een leuk idee/voorbeeld.Op maandag 13 juli 2009 09:42 schreef Iblis het volgende:
[..]
Wel verschillen, geen grote verschillen. Er is een theoretische vorm van de aarde, waar de zwaartekracht potentiaal precies gelijk is. Dat is de geoïde. Idealiter zou, als je b.v. buizen onder het land door zou boren, en het windstil was op oceanen, het water zich precies over die geoïde verdelen.
Die geoïde is weliswaar glad van vorm, maar wel erg onregelmatig. Het simpelste model van de aarde is een bol, een iets verfijnder model is een ellipsoïde, maar de geoïde wijkt daar vanaf:
[ afbeelding ]
Hierboven zie je de vorm van de aarde en de ‘afwijkingen’ van de zwaartekracht zoals die gemeten zijn, dit zijn afwijkingen t.o.v. van de ellipsoïde. Een Gal is een versnelling van 1 cm/s2, dus een milligal 10 micrometer / s2. Dat is vrij weinig t.o.v. de 9.8m/s2 die aangehouden wordt.
Er is n.l. ook een suggestie geweest om dit met het neerleggen van koperdraad te doen in ringen/roosters om de echte Aarde, zodat je dan continu elektrische stroom hebt agv draaing van de Aarde en het Aarde-magnetische veld. D.w.z. Gratis elektriciteit.
quote:Mag je denken, maar het is mijn topic !Op maandag 13 juli 2009 11:20 schreef Haushofer het volgende:
[..]
En jij niet, natuurlijk
Ik denk dat jij wat teveel pretenties hebt
quote:Die buizen zijn vooral conceptueel.
Mooie plaatjes, 1% afwijking vind ik al heel wat. Dat van die buizen vind ik een leuk idee/voorbeeld.
Maar, ho, het gaat niet om 1%! De valversnelling bedraagt zo'n 9,7-9,8m/s2 (afhankelijk van positie richting polen of evenaar), dat is verklaarbaar vanwege de ellipsvorm van de aarde. Daarbij zie je nog een afwijking van 50 milligal. Dat is dus 500 micrometer / s2. Dat is 0,0005 m/s2. Dat is niet 1%
quote:Dat lijkt me voorlopig nogal lastig.Er is n.l. ook een suggestie geweest om dit met het neerleggen van koperdraad te doen in ringen/roosters om de echte Aarde, zodat je dan continu elektrische stroom hebt agv draaing van de Aarde en het Aarde-magnetische veld. D.w.z. Gratis elektriciteit.
[ Bericht 0% gewijzigd door Iblis op 13-07-2009 13:30:56 ]
quote:Het is maar net hoe geloofwaardig je jezelf wilt opstellenOp maandag 13 juli 2009 11:28 schreef Bankfurt het volgende:
[..]
Mag je denken, maar het is mijn topic !
En zoals Iblis zei, je vergist je in je procenten. Zijn plaatje laat zien dat de verschillen door de aardrotatie veel groter zijn. De ART voorspelt dat het roteren van de aarde behalve een centrifugale kracht ook nog framedragging zal veroorzaken, maar dat effect lijkt me buitensporig klein; misschien zit het al in het plaatje van Iblis ingevangen. quote:Er zijn ook metingen verricht van g bij variabele omstandigheden, tijdstippen;Op maandag 13 juli 2009 13:20 schreef Haushofer het volgende:
[..]
Het is maar net hoe geloofwaardig je jezelf wilt opstellen
wat blijkt:
g is locaal gezien, ook variabel in de tijd (dus niet constant !)
Op (n.b. stille) zee, op een schip krijg je nog hele andere uitschieters van g.
Externe omstandigheden hebben uiteraard ? ook invloed, zoals stand van de maan, jaargetijden.
quote:Uitschieters klinkt vrij dramatisch. Alhoewel ik best geloof dat er te meten valt dat g soms verandert, geloof ik niet dat het ook maar enige praktische invloed heeft. Je zult iemand niet horen zeggen ‘potverdorie, nu is m’n taart weer mislukt doordat g vandaag te klein was, daardoor heb ik veel te veel afgewogen!’.
Er zijn ook metingen verricht van g bij variabele omstandigheden, tijdstippen;
wat blijkt:
g is locaal gezien, ook variabel in de tijd (dus niet constant !)
Op (n.b. stille) zee, op een schip krijg je nog hele andere uitschieters van g.
Externe omstandigheden hebben uiteraard ? ook invloed, zoals stand van de maan, jaargetijden.
Zou je deze claim dus eens kunnen onderbouwen met een artikel/boek/meetverslag?
quote:Nee, in die zin dat ik de bron niet weet, maar ik heb het wel gelezen ergens. Ik hoop het alsnog te vinden. De verklaring is een stap verder, en dit heeft wel met water te maken.Op maandag 13 juli 2009 15:59 schreef Iblis het volgende:
[..]
Uitschieters klinkt vrij dramatisch. Alhoewel ik best geloof dat er te meten valt dat g soms verandert, geloof ik niet dat het ook maar enige praktische invloed heeft. Je zult iemand niet horen zeggen ‘potverdorie, nu is m’n taart weer mislukt doordat g vandaag te klein was, daardoor heb ik veel te veel afgewogen!’.
Zou je deze claim dus eens kunnen onderbouwen met een artikel/boek/meetverslag?
quote:Wat voor "uitschieters"? Zoals Iblis zegt, kom maar es met bronnen over de specifieke waarden hiervanOp maandag 13 juli 2009 15:55 schreef Bankfurt het volgende:
[..]
Er zijn ook metingen verricht van g bij variabele omstandigheden, tijdstippen;
wat blijkt:
g is locaal gezien, ook variabel in de tijd (dus niet constant !)
Op (n.b. stille) zee, op een schip krijg je nog hele andere uitschieters van g.
Externe omstandigheden hebben uiteraard ? ook invloed, zoals stand van de maan, jaargetijden.
quote:Zit je niet in de war met het aardmagneetveld? Dat fluctueerd idd over de tijd, en daar was laatst een artikel over van iemand met de hypothese dat dit door oceaanstromen kwam.Op maandag 13 juli 2009 16:06 schreef Bankfurt het volgende:
[..]
Nee, in die zin dat ik de bron niet weet, maar ik heb het wel gelezen ergens. Ik hoop het alsnog te vinden. De verklaring is een stap verder, en dit heeft wel met water te maken.