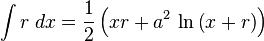SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Nou heb ik net gisteren mijn tentamen analyse achter de rug, echter kon ik 1 som gewoon niet oplossen. Ik kwam er echt niet uit, het betreft:
INT (SQRT(1+cos2x*e2sinx))
Ik had het idee dat deze niet op te lossen valt, maar waarom vragen ze het dan
[ Bericht 18% gewijzigd door McGilles op 17-01-2008 10:45:28 ]
INT (SQRT(1+cos2x*e2sinx))
Ik had het idee dat deze niet op te lossen valt, maar waarom vragen ze het dan
[ Bericht 18% gewijzigd door McGilles op 17-01-2008 10:45:28 ]


Ik zie het ook niet, maar cos2(x)*e2sin(x) = (cos(x)esin(x))2. Misschien dat dat wat verder helpt, maar dat factoriseert verder niet echt makkelijk…quote:Op donderdag 17 januari 2008 10:39 schreef McGilles het volgende:
Nou heb ik net gisteren mijn tentamen analyse achter de rug, echter kon ik 1 som gewoon niet oplossen. Ik kwam er echt niet uit, het betreft:
INT (SQRT(1+cos2x*e2sinx))
Ik had het idee dat deze niet op te lossen valt, maar waarom vragen ze het dan
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


The integrator van Wolfram komt er ook niet echt uit.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Het klopt dat dat het kwadraat is, het komt ook door formule voor de booglengte van de functie:quote:Op donderdag 17 januari 2008 11:13 schreef Iblis het volgende:
[..]
Ik zie het ook niet, maar cos2(x)*e2sin(x) = (cos(x)esin(x))2. Misschien dat dat wat verder helpt, maar dat factoriseert verder niet echt makkelijk…
y = esin(x)
INT (SQRT(1+(dy/dx)2)dx)


Ik neem dus aan dat deze integraal niet te berekenen is?quote:Op donderdag 17 januari 2008 11:29 schreef Iblis het volgende:
The integrator van Wolfram komt er ook niet echt uit.


Het zal sowieso niet makkelijk zijn.quote:Op donderdag 17 januari 2008 12:10 schreef McGilles het volgende:
[..]
Ik neem dus aan dat deze integraal niet te berekenen is?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


sqrt(1+x2) is nog wel te doen met substitutie, eerst u = sqrt(1+x2) en daarna u = cos tquote:Op donderdag 17 januari 2008 12:18 schreef Iblis het volgende:
[..]
Het zal sowieso niet makkelijk zijn.Die computer heeft natuurlijk ook maar een 'gelimiteerd' aantal trucjes en patronen dat hij kent, maar doorgaans kan die site toch wel redelijk complexe integralen aan. Op zich is de vorm sqrt(1 + u^2) wel te integreren, maar met substitutie blijf je nog steeds met een naar gedeelte zitten.
Dan krijg je iets van 1/2 cos-1(sqrt(1+x2)) + 1/4 sin (2cos-1(sqrt(1+x2)))
Maar door die vervelende afgeleide van e2sin(x) krijg ik het niet voor elkaar.


Nee. Als je hebt:quote:Op donderdag 17 januari 2008 14:05 schreef McGilles het volgende:
[..]
sqrt(1+x2) is nog wel te doen met substitutie, eerst u = sqrt(1+x2) en daarna u = cos t
Dan krijg je iets van 1/2 cos-1(sqrt(1+x2)) + 1/4 sin (2cos-1(sqrt(1+x2)))
Dan is:
De primitieve van jouw functie is niet in gesloten vorm uit te drukken. Maar dat betekent niet dat de integraal niet te berekenen is, je kunt de integraal altijd nog numeriek berekenen (c.q. benaderen).quote:Maar door die vervelende afgeleide van e2sin(x) krijg ik het niet voor elkaar.


Maar hier hangt a ook weer van x af op een vervelende manier.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Nee dat is een misverstand. De integraal die ik hierboven geef is een standaardintegraal, waar a een constante is.quote:Op donderdag 17 januari 2008 16:56 schreef Iblis het volgende:
Maar hier hangt a ook weer van x af op een vervelende manier.


Ja, ik zwets. Mijn excuses. Ik dacht dat je voor a^2 die (cos(x)exp(sin(2x)))^2 wilde schrijven, maar dat is natuurlijk nonsens.quote:Op donderdag 17 januari 2008 16:59 schreef Riparius het volgende:
[..]
Nee dat is een misverstand. De integraal die ik hierboven geef is een standaardintegraal, waar a een constante is.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Kan Danny eigenlijk niet eens latex erin zetten ofzo? gaat wat makelijker dan steeds speciale tekens te moeten opnemen selecteren plakken etc...


Je kunt de LaTeX-Previewer van Troy Henderson mis/gebruiken:quote:Op donderdag 17 januari 2008 17:31 schreef Wouser het volgende:
Kan Danny eigenlijk niet eens latex erin zetten ofzo? gaat wat makelijker dan steeds speciale tekens te moeten opnemen selecteren plakken etc...
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Dat zou best maar dat is vast hetzelfde als de functie die ik zei. Met 10 verschillende wiskundige programma's krijg je meestal met primitiveren 8 verschillende soorten antwoorden die eigenlijk allemaal hetzelfde zijn.quote:Op donderdag 17 januari 2008 16:51 schreef Riparius het volgende:
[..]
Nee. Als je hebt:
[ afbeelding ]
Dan is:
[ afbeelding ]
[..]
INT (sqrt(1+x2) dx
INT u2 / (sqrt (u2-1)) du
INT sec3t dt
enz


Nee. De primitieve van √(1 + x2) is niet uit te drukken met de inverse van een goniometrische functie, wel m.b.v. de inverse van een hyperbolische functie. Je bent kennelijk in de war met de primitieve van √(1 - x2).quote:Op donderdag 17 januari 2008 19:07 schreef McGilles het volgende:
[..]
Dat zou best maar dat is vast hetzelfde als de functie die ik zei. Met 10 verschillende wiskundige programma's krijg je meestal met primitiveren 8 verschillende soorten antwoorden die eigenlijk allemaal hetzelfde zijn.
INT (sqrt(1+x2) dx
INT u2 / (sqrt (u2-1)) du
INT sec3t dt
enz


Wat is er mis met:quote:Op donderdag 17 januari 2008 19:57 schreef Riparius het volgende:
[..]
Nee. De primitieve van √(1 + x2) is niet uit te drukken met de inverse van een goniometrische functie, wel m.b.v. de inverse van een hyperbolische functie. Je bent kennelijk in de war met de primitieve van √(1 - x2).
INT sqrt(1+x2)dx
x = tan (t) dx = sec2(t) dt
INT sqrt (1+tan2(t)) sec 2(t) dt =
INT sec 3(t) dt
= 1/2 (secx tanx + ln | secx + tanx| )
= 1/2 (x * sqrt(1+x2) + ln | x + sqrt(1+x2 | )
(terwijl ln | x + sqrt(1+x2 = sinh -1 (x) )
en dit is precies wat wolfram integretor ook geeft!
[ Bericht 18% gewijzigd door McGilles op 17-01-2008 23:42:54 ]


Met de uitkomst is niets mis, maar zoals je ziet heb je hier in de primitieve van √(1 + x2) de inverse van een hyperbolische functie, en niet de inverse van een goniometrische functie. Of is het verschil tussen die twee je niet duidelijk?quote:Op donderdag 17 januari 2008 23:35 schreef McGilles het volgende:
[..]
Wat is er mis met:
INT sqrt(1+x2)dx
x = tan (t) dx = sec2(t) dt
INT sqrt (1+tan2(t)) sec 2(t) dt =
INT sec 3(t) dt
= 1/2 (secx tanx + ln | secx + tanx| )
= 1/2 (x * sqrt(1+x2) + ln | x + sqrt(1+x2 | )
(terwijl ln | x + sqrt(1+x2 = sinh -1 (x) )
en dit is precies wat wolfram integretor ook geeft!


mss valt er iets te regelen met
1 + cos2(x)*e2*sin(x) dx =
1+ cos(x)*e2*sin(x) d(-sin(x)) =
[ Bericht 20% gewijzigd door harrypiel op 18-01-2008 21:48:55 ]
1 + cos2(x)*e2*sin(x) dx =
1+ cos(x)*e2*sin(x) d(-sin(x)) =
[ Bericht 20% gewijzigd door harrypiel op 18-01-2008 21:48:55 ]


Nee, de primitieve van deze functie (of de wortel hieruit) is echt niet in een eindige vorm in elementaire functies uit te drukken, net zo min als de primitieve van bijv. esin x of ex².quote:Op vrijdag 18 januari 2008 21:43 schreef harrypiel het volgende:
mss valt er iets te regelen met
1 + cos2(x)*e2*sin(x) dx =
1+ cos(x)*e2*sin(x) d(-sin(x)) =


weet je dat heel heel zeker? Ik kan namelijk nog verder gaan en tot
SQRT (1 + SQRT(1 - sin2(x)) * e2*sin(x) )d(-sin(x)) =
en dan het minteken in de infinisimaal naar buiten gooien waardoor ik elke sin(x) voor u kan substitueren. Dan krijg ik uiteindelijk -SQRT( 1 + SQRT(1 - u2) * e2*u) d(u) =
[ Bericht 1% gewijzigd door harrypiel op 18-01-2008 22:55:05 ]
SQRT (1 + SQRT(1 - sin2(x)) * e2*sin(x) )d(-sin(x)) =
en dan het minteken in de infinisimaal naar buiten gooien waardoor ik elke sin(x) voor u kan substitueren. Dan krijg ik uiteindelijk -SQRT( 1 + SQRT(1 - u2) * e2*u) d(u) =
[ Bericht 1% gewijzigd door harrypiel op 18-01-2008 22:55:05 ]


Het is leuk en aardig, maar hoe wilde je precies die cos(x) eruit factoriseren? Er staat ook nog een 1 onder het wortelteken.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


door cos(x) als SQRT(1-sin2x) te schijven. we hebben cos2(x)*e2sin(x) dx
Daarvan gooien we een cos(x)-factor voor de d, zodat we cos(x)*e2sin(x) d(-sin(x)) krijgen
De andere cos(x) werken we om naar SQRT(1-sin2(x)) mvb de stelling van pythagoras toegepast op de eenheidscirkel.
[ Bericht 1% gewijzigd door harrypiel op 18-01-2008 23:12:35 ]
Daarvan gooien we een cos(x)-factor voor de d, zodat we cos(x)*e2sin(x) d(-sin(x)) krijgen
De andere cos(x) werken we om naar SQRT(1-sin2(x)) mvb de stelling van pythagoras toegepast op de eenheidscirkel.
[ Bericht 1% gewijzigd door harrypiel op 18-01-2008 23:12:35 ]


Probeer het eens stap voor stap uit te werken, je doet dingen die niet kunnen. Je kunt even willekeurig factors uit een willekeurige term trekken. Je hebt sqrt(1 + iets) staan, dus als je uit ‘iets’ een factor weghaalt, moet je dat ook uit die 1 doen. Zo wil het echt niet.quote:Op vrijdag 18 januari 2008 23:06 schreef harrypiel het volgende:
door cos(x) als SQRT(1-sin2x) te schijven. we hebben cos2(x)*e2sin(x) dx
Daarvan gooien we een cos(x)-factor voor de d, zodat we cos(x)*e2sin(x) d(-sin(x)) krijgen
De andere cos(x) werken we om naar SQRT(1-sin2(x)) mvb de stelling van pythagoras toegepast op de eenheidscirkel.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ja. En dat is niet omdat programma's voor het bepalen van primitieven maar een beperkt aantal trucjes zouden kennen. Lees dit eens even. Je bent trouwens raar aan het goochelen. Ik heb vroeger wel eens een integraal met een e-macht onder het wortelteken voor iemand hier op FOK uitgewerkt (overigens nooit een bedankje voor gehad), waar de primitieve wel in elementaire functies is uit te drukken. Is hier nog na te lezen, misschien steek je er iets van op.quote:Op vrijdag 18 januari 2008 22:49 schreef harrypiel het volgende:
weet je dat heel heel zeker?
[ Bericht 2% gewijzigd door Riparius op 19-01-2008 17:25:34 ]


OK, ik heb ff met een trial functie SQRT(1+e^2x) gestoeid om mn methode te controlen en het werkt idd niet op die manier. Blijkbaar werkt dat alleen om constanten danwel gemeenschappelijke factoren voor je infinisimaal te halen om zo een integratie tot een goed einde te brengen.
En ja, ik heb ook ooit wat gelezen over een algoritme waarmee je kan controleren of een functie te primitieveren valt, als je dat bedoelt met je eerste zin. En wat moet ik in godsnaam met een link naar een friggin idols subforum ?
?
En ja, ik heb ook ooit wat gelezen over een algoritme waarmee je kan controleren of een functie te primitieveren valt, als je dat bedoelt met je eerste zin. En wat moet ik in godsnaam met een link naar een friggin idols subforum


Ik heb een beetje een gevoel dat je een trucje toepast zonder precies te weten wat je doet, maar je past in feite substitutie toe. Dus als je dan u = g(x) substitueert, dan krijg je du/dx = g'(x) => dx = g'(x) du (beetje kwestieuze notatie wellicht, maar gebruikelijk als je Leibniz' notatie gebruikt), dus om de substitutie van dx => du, of, zoals jij meestal laat staan d(g(x)) te volbrengen, moet je 'voor' de dx de geschikte factor g'(x) hebben staan. Die moet je er netjes 'uit kunnen factoriseren'. En in de opgave van deze topic kun je cos(x) niet zo uitfactoriseren, omdat je ook nog de '1' onder wortelteken hebt.quote:Op zaterdag 19 januari 2008 14:52 schreef harrypiel het volgende:
OK, ik heb ff met een trial functie SQRT(1+e^2x) gestoeid om mn methode te controlen en het werkt idd niet op die manier. Blijkbaar werkt dat alleen om constanten danwel gemeenschappelijke factoren voor je infinisimaal te halen om zo een integratie tot een goed einde te brengen.
En ja, ik heb ook ooit wat gelezen over een algoritme waarmee je kan controleren of een functie te primitieveren valt, als je dat bedoelt met je eerste zin. En wat moet ik in godsnaam met een link naar een friggin idols subforum?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Vraagje:
(n-1)/n * (n-2)/n * (n-3)/n * (n-4)/n * enz enz
Kan je dit ook schrijven als 1 mooie formule?
(n-1)/n * (n-2)/n * (n-3)/n * (n-4)/n * enz enz
Kan je dit ook schrijven als 1 mooie formule?


Met die link was even wat misgegaanquote:Op zaterdag 19 januari 2008 14:52 schreef harrypiel het volgende:
En ja, ik heb ook ooit wat gelezen over een algoritme waarmee je kan controleren of een functie te primitieveren valt, als je dat bedoelt met je eerste zin. En wat moet ik in godsnaam met een link naar een friggin idols subforum?


Je zou iets met een faculteit en een n^x in de noemer kunnen klussen. D.w.z. n!/(k!n^(n-k)) (ik vergis me vast ergens...quote:Op zaterdag 19 januari 2008 17:26 schreef McGilles het volgende:
Vraagje:
(n-1)/n * (n-2)/n * (n-3)/n * (n-4)/n * enz enz
Kan je dit ook schrijven als 1 mooie formule?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Oooh damn wat dom dat ik dat over het hoofd zagquote:Op zaterdag 19 januari 2008 17:36 schreef Iblis het volgende:
[..]
Je zou iets met een faculteit en een n^x in de noemer kunnen klussen. D.w.z. n!/(k!n^(n-k)) (ik vergis me vast ergens...)


Kleine vergissing inderdaad als jouw n dezelfde is als die van McGilles; door in de teller al een n! te zetten, heb je in ieder geval een factor n daar die je met een k! niet meer wegkrijgt. Ik kom op (n-1)! / (nk*(n-k-1)!).quote:Op zaterdag 19 januari 2008 17:36 schreef Iblis het volgende:
[..]
Je zou iets met een faculteit en een n^x in de noemer kunnen klussen. D.w.z. n!/(k!n^(n-k)) (ik vergis me vast ergens...)
Ik vraag me wel af waar je deze formule voor nodig hebt, in de kansrekening valt vaak een noemer uit de ene term weg tegen de teller van de volgende term.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja, ik had al het vermoeden dat ik ergens een off-by-one error zou maken, maar hey, ik had er even geen zin om er te hard over na te denken. 
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik vroeg me gewoon af als je een x aantal mensen hebt wat de kans is dat er mensen bij zitten met dezelfde geboortedatum. Dus ik ging vrolijk even excel openen en toen liep ik vast, dom overigensquote:Op zaterdag 19 januari 2008 17:59 schreef GlowMouse het volgende:
[..]
Kleine vergissing inderdaad als jouw n dezelfde is als die van McGilles; door in de teller al een n! te zetten, heb je in ieder geval een factor n daar die je met een k! niet meer wegkrijgt. Ik kom op (n-1)! / (nk*(n-k-1)!).
Ik vraag me wel af waar je deze formule voor nodig hebt, in de kansrekening valt vaak een noemer uit de ene term weg tegen de teller van de volgende term.
Nu heb ik de kloppende formule zelf even bedacht, alleen kan excel maar maximaal 170! uitrekenen, bij 171! zegt ie dat hij het niet kan


Een vraagje over radioactiviteit. Er wordt in mijn boek gezegd dat "het in de scheikunde onmogelijk is om een element om te zetten in een ander element" en dat bij een kernreactie de atoomkern van samenstelling verandert.
Maar als je Th-232 neemt en dat stoot een alfadeeltje af, verliest het twee protonen en twee neutronen. De kern verandert dus. Het atoomnummer verandert dus ook en daarmee eigenlijk ook de stof (alleen dat kan dus niet). Hoe moet ik het me dan voorstellen dat wel de kern verandert, maar niet de stof zelf. Kun je dan bijvoorbeeld een koolstofkern in een zuurstofatoom hebben ofzo ?
Maar als je Th-232 neemt en dat stoot een alfadeeltje af, verliest het twee protonen en twee neutronen. De kern verandert dus. Het atoomnummer verandert dus ook en daarmee eigenlijk ook de stof (alleen dat kan dus niet). Hoe moet ik het me dan voorstellen dat wel de kern verandert, maar niet de stof zelf. Kun je dan bijvoorbeeld een koolstofkern in een zuurstofatoom hebben ofzo ?


De eerste uitspraak heeft waarschijnlijk betrekking op chemische reacties. Kernverval is van natuurkundige aard, daardoor verandert thorium uiteindelijk in lood.quote:Op zaterdag 19 januari 2008 19:22 schreef MeScott het volgende:
Een vraagje over radioactiviteit. Er wordt in mijn boek gezegd dat "het in de scheikunde onmogelijk is om een element om te zetten in een ander element" en dat bij een kernreactie de atoomkern van samenstelling verandert.
Maar als je Th-232 neemt en dat stoot een alfadeeltje af, verliest het twee protonen en twee neutronen. De kern verandert dus. Het atoomnummer verandert dus ook en daarmee eigenlijk ook de stof (alleen dat kan dus niet). Hoe moet ik het me dan voorstellen dat wel de kern verandert, maar niet de stof zelf. Kun je dan bijvoorbeeld een koolstofkern in een zuurstofatoom hebben ofzo ?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


De stof verandert wel. Het is chemisch gezien een andere stof. Maar dit is geen ‘chemische reactie’. Kernfysica is weer het gebied van de natuurkunde. Dus je boek wil eigenlijk zeggen dat in de ‘traditionele’ scheikunde er niet vanuit gegaan wordt dat elementen veranderen, atomen kunnen herschikken tot nieuwe moleculen, maar de protonen en neutronen niet tot nieuwe atomen. Dat is weer het ‘domein’ van de kernfysica.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik doe verder niks in de scheikunde, maar voor zover ik weet kan een element na het uitstoten van bijvoorbeeld een alfadeeltje overgaan naar een andere stof. Bijvoorbeeld Thorium naar Radium.quote:Op zaterdag 19 januari 2008 19:22 schreef MeScott het volgende:
Een vraagje over radioactiviteit. Er wordt in mijn boek gezegd dat "het in de scheikunde onmogelijk is om een element om te zetten in een ander element" en dat bij een kernreactie de atoomkern van samenstelling verandert.
Maar als je Th-232 neemt en dat stoot een alfadeeltje af, verliest het twee protonen en twee neutronen. De kern verandert dus. Het atoomnummer verandert dus ook en daarmee eigenlijk ook de stof (alleen dat kan dus niet). Hoe moet ik het me dan voorstellen dat wel de kern verandert, maar niet de stof zelf. Kun je dan bijvoorbeeld een koolstofkern in een zuurstofatoom hebben ofzo ?


Letterlijk citaat:
Het komt er dus op neer dat in een chemische reactie geen element kan veranderen in een andere, maar in de "kernfysica" wel ?quote:Door het uitstoten van het alfadeeltje neemt het aantal kerndeeltjes met 4 en het aantal protonen met 2 af. De nieuwe atoomkern bevat dan 228 kerndeeltjes, waaronder 88 protonen.
(...)
Deze reactie is geen chemische reactie, want in de scheikunde is het onmogelijk om een element om te zetten in een ander element. Omdat bij bovenstaande reactie een atoomkern verandert, noemen we dit een kernreactie.


Inderdaad. Zie ook de definitie van een chemische reactie.quote:Op zaterdag 19 januari 2008 19:43 schreef MeScott het volgende:
Letterlijk citaat:
[..]
Het komt er dus op neer dat in een chemische reactie geen element kan veranderen in een andere, maar in de "kernfysica" wel ?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


INT sqrt(1+e^x) is zo moeilijk toch niet?quote:Op zaterdag 19 januari 2008 04:33 schreef Riparius het volgende:
[..]
Ik heb vroeger wel eens een integraal met een e-macht onder het wortelteken voor iemand hier op FOK uitgewerkt (overigens nooit een bedankje voor gehad), waar de primitieve wel in elementaire functies is uit te drukken.


Nee, maar voor de persoon die de vraag destijds stelde kennelijk wel. En er ontstaat ook vaak verwarring doordat verschillende programma's de primitieve op verschillende manieren uitdrukken.quote:Op zaterdag 19 januari 2008 19:53 schreef McGilles het volgende:
[..]
INT sqrt(1+e^x) is zo moeilijk toch niet?


Dat is zeker zo. Soms is het lastig te ontdekken of bepaalde primitieven hetzelfde zijn, zeker als ze wat complexer zijnquote:Op zaterdag 19 januari 2008 19:59 schreef Riparius het volgende:
[..]
Nee, maar voor de persoon die de vraag destijds stelde kennelijk wel. En er ontstaat ook vaak verwarring doordat verschillende programma's de primitieve op verschillende manieren uitdrukken.


Ah, dan snap ik hetquote:Op zaterdag 19 januari 2008 19:46 schreef GlowMouse het volgende:
[..]
Inderdaad. Zie ook de definitie van een chemische reactie.
[ Bericht 53% gewijzigd door MeScott op 19-01-2008 21:41:32 ]


Hello!
Stel dat het levensduur van sommige elektronica componenten is exponentieel verdeeld met paramter 1/s, dus:
f(t|s)=(1/s)exp(-t/s) met t >=0.
Vijf nieuwe componenten worden getest, het eerste ging al stuk na 100 dagen, er zijn verder geen observaties genoteerd.
a.Wat is de likelihood functie van s?
b.wat is de mle van s?
c.wat is de sampling distribution van de mle?
(vertalen van die woordjes is hopelijk niet nodig!)
Kan iemand helpen met deze vragen? Ik twijfel aan mijn uitwerking
alvast bedankt
Stel dat het levensduur van sommige elektronica componenten is exponentieel verdeeld met paramter 1/s, dus:
f(t|s)=(1/s)exp(-t/s) met t >=0.
Vijf nieuwe componenten worden getest, het eerste ging al stuk na 100 dagen, er zijn verder geen observaties genoteerd.
a.Wat is de likelihood functie van s?
b.wat is de mle van s?
c.wat is de sampling distribution van de mle?
(vertalen van die woordjes is hopelijk niet nodig!)
Kan iemand helpen met deze vragen? Ik twijfel aan mijn uitwerking
alvast bedankt
verlegen :)


Noem de observaties Xi (i=1,..,n)
a. L(s) = Πi=1n f(Xi; s) = (1/s)n*exp(-1/s * Σi=1nXi)
b. argmaxsL(s) = 1/n * Σi=1nXi (via d/ds L(s) = 0)
c. Gamma-verdeling (aan te tonen via bijvoorbeeld de mgf)
[ Bericht 2% gewijzigd door GlowMouse op 20-01-2008 23:05:32 ]
a. L(s) = Πi=1n f(Xi; s) = (1/s)n*exp(-1/s * Σi=1nXi)
b. argmaxsL(s) = 1/n * Σi=1nXi (via d/ds L(s) = 0)
c. Gamma-verdeling (aan te tonen via bijvoorbeeld de mgf)
[ Bericht 2% gewijzigd door GlowMouse op 20-01-2008 23:05:32 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hoe zou je het volgende vertalen: "the positron scatters in the tissue losing energy" ?
Wat is de correcte Nederlandse vertaling voor 'scatters' in deze context?
Wat is de correcte Nederlandse vertaling voor 'scatters' in deze context?


a) Okey, dit had ik al gelukkig. Nu voor het speciaal geval dat n=5.quote:Op zondag 20 januari 2008 22:47 schreef GlowMouse het volgende:
Noem de observaties Xi (i=1,..,n)
a. L(s) = Πi=1n f(Xi; s) = (1/s)n*exp(-1/s * Σi=1nXi)
b. argmaxsL(s) = 1/n * Σi=1nXi (via d/ds L(s) = 0)
c. Gamma-verdeling (aan te tonen via bijvoorbeeld de mgf)
b) de mle vind je door de logartime te nemen van antwoord in a) naar s te differentieren en dan gelijk stellen aan 0, dan oplossen.
c)hoe moet ik dit alweer doen?
de antwoorden (zonder uitwerking) zoals in het boek.
a) 5/s exp(-5t/s).
b) s'hoedje'=5T
c)s'hoedje' ~ exp(1/s) (de verdeling).
verlegen :)


De vraagstelling vond ik al tricky, maar nu ik de antwoorden zie klopt dat ook. Achteraf bedenk je je dat je een schatter ook kunt baseren op alleen de kleinste waarneming (die een exp(n/s)-verdeling heeft, kun je aantonen via bijvoorbeeld de cdf), terwijl je zulk soort dingen juist moet beslissen voordat je enige data hebt omdat je schatter anders allerlei optimale eigenschappen mist. Het antwoord vind ik daarom dubieus.
A en b zijn duidelijk bij één trekking uit een exp(5/s)-verdeling. Bij c krijg je dat 5*T met T~exp(5/s) weer exp(1/s) verdeeld is.
A en b zijn duidelijk bij één trekking uit een exp(5/s)-verdeling. Bij c krijg je dat 5*T met T~exp(5/s) weer exp(1/s) verdeeld is.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik denk dat je zou kunnen zeggen dat het positron verstrooit, of dat je over de verstrooiing van het positron zou kunnen spreken.quote:Op maandag 21 januari 2008 10:24 schreef Kang-He het volgende:
Hoe zou je het volgende vertalen: "the positron scatters in the tissue losing energy" ?
Wat is de correcte Nederlandse vertaling voor 'scatters' in deze context?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


soms staat iets als: 'under appropriate smoothness condition on f, the mle from an i.i.d sample is consistent.
In het bewijs wordt een integraal met een afgeleide verwisseld. Ik vraag me af..wat de 'appropriate somoothness condition' zou zijn. IK denk zelf: f is uniform continu. Maar zijn er misschien andere condities?
In het bewijs wordt een integraal met een afgeleide verwisseld. Ik vraag me af..wat de 'appropriate somoothness condition' zou zijn. IK denk zelf: f is uniform continu. Maar zijn er misschien andere condities?
verlegen :)