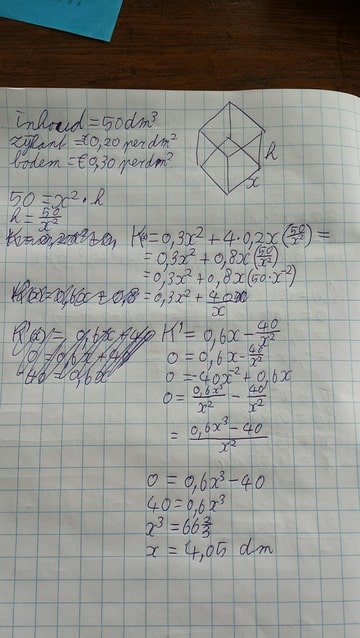[Bèta wiskunde] Huiswerk- en vragentopic.

woensdag 13 januari 2016 @ 22:18:52 #51

netchip

Nu heb ik ook geen college, dus dat helpt ook al niet echt mee.

woensdag 13 januari 2016 @ 22:25:07 #52

Anoonumos

quote:
Op woensdag 13 januari 2016 22:18 schreef netchip het volgende:
Nu heb ik ook geen college, dus dat helpt ook al niet echt mee.

Verzamelingen zijn gelijk als ze dezelfde elementen hebben

Dus laten zien dat elk element in de linkerzijde ook in de rechterzijde zit, en andersom

woensdag 13 januari 2016 @ 22:33:16 #53

netchip

quote:
Op woensdag 13 januari 2016 22:25 schreef Anoonumos het volgende:

[..]

Verzamelingen zijn gelijk als ze dezelfde elementen hebben

Dus laten zien dat elk element in de linkerzijde ook in de rechterzijde zit, en andersom

Te bewijzen: $(A\cap B)^c = A^c \cup B^c$
Dan moet gelden dat $(A\cap B)^c$ een deelverzameling is van $A^c \cup B^c$ , en andersom. Dit had ik al bedacht. Ik nam aan dat er een x is in A en B, zodat x een element is van de doorsnede van A en B. Omdat dit element niet in zowel A^c als B^c zit, zal deze ook niet in de vereniging van deze verzamelingen zitten.

Ergens gaat er hier iets mis en mis ik wat. Welk geval ben ik vergeten?

woensdag 13 januari 2016 @ 22:43:17 #54

Anoonumos

quote:
Op woensdag 13 januari 2016 22:33 schreef netchip het volgende:

[..]

Te bewijzen: $(A\cap B)^c = A^c \cup B^c$
Dan moet gelden dat $(A\cap B)^c$ een deelverzameling is van $A^c \cup B^c$ , en andersom. Dit had ik al bedacht. Ik nam aan dat er een x is in A en B, zodat x een element is van de doorsnede van A en B. Omdat dit element niet in zowel A^c als B^c zit, zal deze ook niet in de vereniging van deze verzamelingen zitten.

Ergens gaat er hier iets mis en mis ik wat. Welk geval ben ik vergeten?

Uh omdat links $(A\cap B)^c$ is en niet $(A\cap B)$ ?

woensdag 13 januari 2016 @ 22:48:34 #55

netchip

quote:
Op woensdag 13 januari 2016 22:43 schreef Anoonumos het volgende:

[..]

Uh omdat links $(A\cap B)^c$ is en niet $(A\cap B)$ ?

Uhu maar als x in $(A\cap B)$ zit, dan zit deze niet in $(A\cap B)^c$ . Dus dan kunnen we toch concluderen dat x geen element is van de linkerzijde, en niet van de rechterzijde?

woensdag 13 januari 2016 @ 23:09:49 #56

Anoonumos

quote:
Op woensdag 13 januari 2016 22:48 schreef netchip het volgende:

[..]

Uhu maar als x in $(A\cap B)$ zit, dan zit deze niet in $(A\cap B)^c$ . Dus dan kunnen we toch concluderen dat x geen element is van de linkerzijde, en niet van de rechterzijde?

Ja het klopt wel, maar je schiet er niet veel mee op.

Je wilde laten dat $(A\cap B)^c$ een deelverzameling is van $A^c \cup B^c$
dus neem x in $(A\cap B)^c$

woensdag 13 januari 2016 @ 23:14:20 #57

Anoonumos

Maar goed iedereen stoeit ermee de eerste week

nu is het triviaal lolz

woensdag 13 januari 2016 @ 23:19:57 #58

Diacetylmorfine

quote:
Op woensdag 13 januari 2016 16:16 schreef thabit het volgende:

[..]

P in X-A en Q in A kun je open delen U en V vinden. Maar die V beeldt daarmee nog niet op een open deel in X/A af. Je moet de compactheid gebruiken om open delen in X te vinden die ook naar open delen in X/A afbeelden.

Ik ga er morgen met pen en papier nog een keer goed voor zitten. Alvast bedankt!

quote:
Op woensdag 13 januari 2016 22:17 schreef netchip het volgende:
Hoe kun je het beste leren bewijzen? Ik doe nu het Wiskundige Structuren dictaat van de Universiteit Leiden, maar bij het bewijzen van de wetten van De Morgan liep ik al vast. Eerste bewijsopgave in het dictaat. Ik heb geen idee waar ik moet beginnen bij zoiets...

Oefenen. Heel veel. En voordat je begint aan een bewijs zorgen dat je een goed begrip hebt van de definities en stellingen die je tot je beschikking hebt, maar bovenal een goed beeld van wát je wil bewijzen. Als je er niet uit komt noteren wat je weet, of je afvragen wat er mis zou gaan als je stelling niet zou kloppen. Verder niet opgeven voor je het gevoel hebt dat je je bronnen uitgeput hebt.

Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caparet

zaterdag 16 januari 2016 @ 16:29:48 #59

XXL-Puntenslijper

$\int e^{\cos x} \cdot \sin 2x$ $dx$
$\sin 2x = 2\sin x \cdot \cos x$
$\int e^{\cos x} \cdot 2\sin x \cdot \cos x$ $dx$
substitueer $u = \cos x$ , $u' = -\sin x$
$-2 \int e^u \cdot \cos x$
En dan zou ik integration by parts gebruiken, maar nou moet je dit doen:
$z = u$ , $z' = 1$
En dan pas integration by parts.
Hoe moet ik nou weten wanneer je dit soort trucjes moet toepassen?
http://www.wolframalpha.com/input/?i=integral+e^cosx+*+sin2x

zaterdag 16 januari 2016 @ 17:29:13 #60

Anoonumos

z = u
dat is gewoon andere notatie?

zaterdag 16 januari 2016 @ 18:11:54 #61

Riparius

quote:
Op zaterdag 16 januari 2016 16:29 schreef XXL-Puntenslijper het volgende:
$\int e^{\cos x} \cdot \sin 2x \mathrm{d}x$

Doe het als volgt. Je hebt

$\frac{\rm{d}(e^{\cos\,x})}{\rm{d}x}\,=\,-e^{\cos\,x}\cdot\sin\,x$

zodat

$\rm{d}(e^{\cos\,x})\,=\,-e^{\cos\,x}\cdot\sin\,x\rm{d}x$

en aangezien

$\sin\,2x\,=\,2\cdot\sin\,x\cdot\cos\,x$

hebben we dus

$\int e^{\cos x} \cdot \sin\,2x \rm{d}x\,=\,-2\cdot\int \cos\,x\rm{d}(e^{\cos\,x})$

Nu kunnen we gebruik maken van

$\int u\rm{d}v\,=\,uv\,-\,\int v\rm{d}u$

met

$u\,=\,\cos\,x$

en

$v\,=\,e^{\cos\,x}$

zodat

$\int e^{\cos x} \cdot \sin 2x \rm{d}x\,=\,-2\cdot\int \cos\,x\rm{d}(e^{\cos\,x})\,=\,-2\cdot\left(\cos\,x\cdot e^{\cos\,x}\,-\,\int e^{\cos\,x}\rm{d}(cos\,x)\right)$

en dus

$\int e^{\cos x} \cdot \sin 2x \rm{d}x\,=\,-2\cdot\left(\cos\,x\cdot e^{\cos\,x}\,-\,e^{\cos\,x}\right)\,+\,C\,=\,-2\cdot e^{\cos\,x}\cdot(\cos\,x\,-\,1)\,+\,C$

Ik heb hier gebruik gemaakt van partiële integratie, maar ook van een impliciete substitutie. Als deze techniek je niet duidelijk is, bestudeer dan eens deze post van mij.

[ Bericht 0% gewijzigd door Riparius op 18-01-2016 14:51:43 ]

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

dinsdag 19 januari 2016 @ 14:47:30 #62

Boarderzip

Ik heb een vraag uit een oefententamen wiskunde waar ik met een klasgenoot samen maar niet uit kom, ik denk nu het goede antwoord gevonden te hebben. We hebben geen uitwerking en ook niet het antwoord van onze leraar gekregen vandaar dat ik het hier kom vragen. Dit is mijn uitwerking:

Het is de bedoeling om de optimale afmetingen van de doos te vinden waarbij de totale materiaalkosten minimaal zijn.

[ Bericht 16% gewijzigd door Boarderzip op 19-01-2016 15:15:28 (Foutje in uitwerking) ]

dinsdag 19 januari 2016 @ 15:31:25 #63

Riparius

quote:
Op dinsdag 19 januari 2016 14:47 schreef Boarderzip het volgende:
Ik heb een vraag uit een oefententamen wiskunde waar ik met een klasgenoot samen maar niet uit kom, ik denk nu het goede antwoord gevonden te hebben. We hebben geen uitwerking en ook niet het antwoord van onze leraar gekregen vandaar dat ik het hier kom vragen. Dit is mijn uitwerking:

[ afbeelding ]

Het is de bedoeling om de optimale afmetingen van de doos te vinden waarbij de totale materiaalkosten minimaal zijn.

Post eens een foto van de originele opgave. Heeft de doos geen deksel?

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

dinsdag 19 januari 2016 @ 15:35:18 #64

Boarderzip

quote:
Op dinsdag 19 januari 2016 15:31 schreef Riparius het volgende:

[..]

Post eens een foto van de originele opgave. Heeft de doos geen deksel?

De doos heeft geen deksel, hierbij de opgave:

De afmetingen van de doos zijn dus volgens mij 4,05 dm lang, 4,05 dm breed en 3,04 dm hoog.

dinsdag 19 januari 2016 @ 15:41:20 #65

Riparius

quote:
Op dinsdag 19 januari 2016 15:35 schreef Boarderzip het volgende:

[..]

De doos heeft geen deksel, hierbij de opgave:

[ afbeelding ]

De afmetingen van de doos zijn dus volgens mij 4,05 dm lang, 4,05 dm breed en 3,04 dm hoog.

Je uitwerking lijkt me correct. Je moet alleen nog laten zien dat je kostenfunctie K(x) voor x ≈ 4,05 inderdaad een minimum aanneemt. Waarom twijfel je?

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

dinsdag 19 januari 2016 @ 15:44:12 #66

Boarderzip

quote:
Op dinsdag 19 januari 2016 15:41 schreef Riparius het volgende:

[..]

Je uitwerking lijkt me correct. Je moet alleen nog laten zien dat je kostenfunctie K(x) voor x ≈ 4,05 inderdaad een minimum aanneemt. Waarom twijfel je?

Ik twijfel omdat ik geen controle mogelijkheid heb, geen van mijn klasgenoten kwam eruit. De afgelopen 2 dagen ben ik ook 5x opnieuw begonnen dus vandaar. Bedankt voor je antwoord, ik ben blij dat het gelukt is, op naar het tentamen morgen

woensdag 27 januari 2016 @ 10:48:44 #67

Zwelgje84

Ik had al een eigen topic gemaakt, maar volgens mij hoort de volgende vraag hier:

Hallo,

Ik heb een vraag over een kansberekening, ik hoop dat jullie me er bij kunnen helpen. Stel je hebt een pot met 100 knikkers. Eén ervan is geel. Elke dag pak je 10 knikkers uit de pot. Hoe groot is dan de kans dat de gele knikker na zes dagen nog in de pot zit? Ik kwam tot hier:

Dag 1 = kans van 0.1 dat de gele knikker gepakt wordt. 90 knikkers over.
Dag 2 = kans van 0.11 dat de gele knikker gepakt wordt. 80 knikkers over
Dag 3 = kans van 0.13 dat de gele knikker gepakt wordt. 70 knikkers over.
Dag 4 = kans van 0.15 dat de gele knikker gepakt wordt. 60 knikkers over.
Dag 5 = kans van 0.17 dat de gele knikker gepakt wordt. 50 knikkers over.
Dag 6 = kans van 0.2 dat de gele knikker gepakt wordt. 40 knikkers over.

Maar hoe tel ik vervolgens de kansen op, of vermenigvuldig ik ze, om er achter te komen wat de totale kans is dat de gele knikker na dag 6 nog in de pot zit?

Alvast bedankt!

woensdag 27 januari 2016 @ 11:09:29 #68

RRuben

Kwaliteitsuser

quote:
Op woensdag 27 januari 2016 10:48 schreef Zwelgje84 het volgende:
Ik had al een eigen topic gemaakt, maar volgens mij hoort de volgende vraag hier:

Hallo,

Ik heb een vraag over een kansberekening, ik hoop dat jullie me er bij kunnen helpen. Stel je hebt een pot met 100 knikkers. Eén ervan is geel. Elke dag pak je 10 knikkers uit de pot. Hoe groot is dan de kans dat de gele knikker na zes dagen nog in de pot zit? Ik kwam tot hier:

Dag 1 = kans van 0.1 dat de gele knikker gepakt wordt. 90 knikkers over.
Dag 2 = kans van 0.11 dat de gele knikker gepakt wordt. 80 knikkers over
Dag 3 = kans van 0.13 dat de gele knikker gepakt wordt. 70 knikkers over.
Dag 4 = kans van 0.15 dat de gele knikker gepakt wordt. 60 knikkers over.
Dag 5 = kans van 0.17 dat de gele knikker gepakt wordt. 50 knikkers over.
Dag 6 = kans van 0.2 dat de gele knikker gepakt wordt. 40 knikkers over.

Maar hoe tel ik vervolgens de kansen op, of vermenigvuldig ik ze, om er achter te komen wat de totale kans is dat de gele knikker na dag 6 nog in de pot zit?

Alvast bedankt!

Volgens mij kan je het probleem beter bekijken als een pot met 99 (bijv.) rode knikkers en 1 gele knikker. Vervolgens pak je 60 knikkers zonder terugleggen. Wat is de kans dat de gele nog niet gepakt is?

Volgens mij (kansrekenen is alweer een beetje weggezakt) is de kans dan 99/100 * 98/99 etc. Dit kan je ook handiger schrijven met faculteiten enzo, maar geen idee hoe dat ook alweer moet.

leef de leven

donderdag 28 januari 2016 @ 18:00:22 #69

thenxero

Het is vast triviaal, maar ik zie het niet...

In dit linkje, onder vergelijking (1), wordt er gezegd "A normal vector to this surface is given by...".

Hoe zie ik dit in?

Met loodrecht op de grafiek wordt denk ik bedoeld loodrecht op (x,y,z(x,y)). Dus het inproduct daarmee zou 0 moeten zijn. Maar dat snap ik niet.

donderdag 28 januari 2016 @ 18:10:19 #70

thabit

quote:
Op donderdag 28 januari 2016 18:00 schreef thenxero het volgende:
Het is vast triviaal, maar ik zie het niet...

In dit linkje, onder vergelijking (1), wordt er gezegd "A normal vector to this surface is given by...".

Hoe zie ik dit in?

Met loodrecht op de grafiek wordt denk ik bedoeld loodrecht op (x,y,z(x,y)). Dus het inproduct daarmee zou 0 moeten zijn. Maar dat snap ik niet.

Een vergelijking voor het raakvlak aan (a, b, f(a,b)) is
$z \,=\, f(a,b) \,+\, \frac{\partial f}{\partial x}(a,b)\cdot(x-a) \,+\, \frac{\partial f}{\partial y}(a,b)\cdot(y-b).$

donderdag 28 januari 2016 @ 18:33:26 #71

thenxero

quote:
Op donderdag 28 januari 2016 18:10 schreef thabit het volgende:

[..]

Een vergelijking voor het raakvlak aan (a, b, f(a,b)) is
$z \,=\, f(a,b) \,+\, \frac{\partial f}{\partial x}(a,b)\cdot(x-a) \,+\, \frac{\partial f}{\partial y}(a,b)\cdot(y-b).$

Haha, ik zie het al. Bedankt.

woensdag 3 februari 2016 @ 13:09:15 #72

obsama

Hoe bepaald je bij een multivariate functie of hij continue is?

voorbeeld:

f(x,y) = abs(xy)

Ik heb vroeger wel geleerd hoe je kan controleren of een functie continue is op een bepaald punt door vanaf beide zijden dat punt te benaderen en dan zou je op hetzelfde antwoord moeten uitkomen.

Alleen hoe bewijs ik dit voor een gehele functie? En vooral hoe bewijs ik dit met meerdere variabelen?

woensdag 3 februari 2016 @ 14:00:35 #73

elena1997

Hii, wij zijn nu op school bij het hoofdstuk verbanden. nu moet ik nog een aantal opdrachten afronden voor morgen.. :blush:
Ik loop bij een vraagje steeds vast en dat is bij onderstaande vraag :

Bij een bloedproef bleek er bij iemand 1,5 promille alcohol in zijn bloed te zitten.
Met de formule kun je uitrekenen hoeveel promille alcohol er na een aantal uren nog in zijn bloed zit.
Hoeveel is dat na 4 uur? Rond je antwoord af op 2 decimalen.

De formule is : R=S X0,5 (0,2Xt)

R = rest
S = starthoeveelheid
T = tijd in uren nu staat die (0,2xt) iets boven de 0,5.. ik heb geen idee hoe ik dit moet uitrekenen
is er iemand die mij kan helpen?

Liefs, xox
Bewerk bericht

woensdag 3 februari 2016 @ 14:34:29 #74

Anoonumos

quote:
Op woensdag 3 februari 2016 14:00 schreef elena1997 het volgende:
nu staat die (0,2xt) iets boven de 0,5.. ik heb geen idee hoe ik dit moet uitrekenen

Dat is een exponent

0.5 ^ (0.2 * t) invullen op je rekenmachine

zondag 14 februari 2016 @ 13:42:38 #75

netchip

Voor de stelling dat er getallen a,b in N zijn met b ≠ 0 en q,r in N zodat a = qb+r en bovendien 0 ≤ r < b, wordt het volgende bewijs gegeven:
De verzameling S = { a, a-b, a-2b, a-3b, ... } heeft een kleinste natuurlijk getal in zich, namelijk r = a-qb voor een zekere q. Dan geldt r-b < 0 dus r = b.

Maar stel nu dat het kleinste natuurlijke getal in S 0 is, dan trek je een natuurlijk getal b > 0 ervan af, en dan krijg je dus een getal kleiner dan 0. Hoe zit dit?

[ Bericht 0% gewijzigd door netchip op 14-02-2016 13:50:41 ]

Forum Opties
Forumhop:
Hop naar:	(afkorting, bv 'KLB')

» school, studie en onderwijs

» school, studie en onderwijs