[Bèta wiskunde] Huiswerk- en vragentopic.

quote:

Op zaterdag 13 september 2014 20:13 schreef Super-B het volgende:

[..]

Vanaf welke stap?

Vanaf het begin, aangezien je niet verder bent gekomen.

quote:

Op zaterdag 13 september 2014 14:43 schreef Super-B het volgende:

[..]

Vermenigvuldigingsteken moest tussen de laatste twee grondgetallen (3).

Schrijf het nog eens op, want ik heb nu geen idee waar je het over hebt.
En zet er ook eens bij welke regel je gebruikt.

quote:

Op zaterdag 13 september 2014 13:20 schreef Super-B het volgende:

[..]

Ik beheers het kwadraat afsplitsing wel, want mij alleen verbaast is dat je het toepast bij x² - 2x = 1, aangezien de kwadraat afsplitsing meestal gebruikt wordt wanneer de c niet een goed getal is om te factoriseren (toch?).

Ik betwijfel of je het wel begrijpt. De vergelijking x² − 2x = 1 is niet (eenvoudig) op te lossen via ontbinden in factoren maar juist prima via kwadraatafsplitsing (die overigens altijd toepasbaar is om een vierkantsvergelijking op te lossen). Ik wil je sterk aanbevelen deze recente post van mij eens goed door te nemen.

quote:

die 1 komt omdat ln 0 is wanneer ln = 1 toch?

Ik begrijp wat je wil zeggen maar zo mag je dit niet opschrijven. Je bedoelt te zeggen dat ln x = 0 equivalent is met x = 1, dus zeg dat dan ook.

Een logaritme van een gegeven getal is niets anders dan een exponent, namelijk de exponent waartoe je een vast getal (het grondtal van de logaritme) moet verheffen om het gegeven getal te verkrijgen. Voor de natuurlijke logaritme, aangegeven met het functiesymbool ln (dat staat voor logarithmus naturalis) is het grondtal het bijzondere getal e. Het getal e is zo bijzonder omdat e het enige (positieve, reële) getal is waarvoor geldt dat de grafiek van f(x) = e^x in elk punt precies even steil loopt als de functiewaarde voor dat punt aangeeft. De functie f(x) = e^x heeft dus zichzelf als afgeleide.

De uitspraak

ln x = y

betekent niets anders dan dat y de exponent is waartoe we e moeten verheffen om x te krijgen, dus

e^y = x

Zo zie je gemakkelijk dat ln 1 = 0, want 0 is immers de exponent waartoe we e moeten verheffen om 1 te krijgen: e⁰ = 1. Ook zie je zo gemakkelijk dat ln e = 1, want we moeten e tot de macht 1 verheffen om e te krijgen: e¹ = e.

Alle rekenregels die gelden voor het werken met logaritmen volgen gemakkelijk uit de rekenregels voor het werken met machten, want een logaritme is immers niets anders dan een exponent.

Heb je bijvoorbeeld

ln a = p, ln b = q

dan betekent dit

e^p = a, e^q = b

Maar dan is dus ook

e^p·e^q = ab

En omdat exponenten optellen bij het vermenigvuldigen van twee machten met hetzelfde grondtal hebben we dus

e^p+q = ab

Maar als het zo is dat je e moet verheffen tot de macht p + q om ab te krijgen, dan betekent dit niets anders dan dat de natuurlijke logaritme van ab gelijk is aan p + q, dus

ln ab = p + q

Maar nu is p = ln a en q = ln b zodat we dus hebben

ln ab = ln a + ln b

Je ziet dus dat de bekende regel die zegt dat de (natuurlijke) logaritme van een product van twee (positieve, reële) getallen gelijk is aan de som van de (natuurlijke) logaritmen van elk van de factoren niets anders is dan een andere gedaante van de regel die zegt dat exponenten optellen bij vermenigvuldiging van twee machten van hetzelfde grondtal. Op een soortgelijke manier zijn ook alle andere rekenregels voor logaritmen af te leiden uit rekenregels voor het werken met machten.

[ Bericht 0% gewijzigd door Riparius op 13-09-2014 21:50:51 ]

quote:

Op zaterdag 13 september 2014 14:36 schreef Super-B het volgende:
Nog één voor het oplossen van x:

4^x - 4^x-1 = 3^x+1 - 3^x

Ik heb dit herschreven tot:

4^x - 4^x * 4^-1 = 3^x * 3¹ - 3^x

Dit is al fout, want je had in het rechterlid een product waar je een minteken moet hebben, maar dit zal wellicht een verschrijving zijn (die niettemin verraadt dat je niet zorgvuldig genoeg werkt).

quote:

Dit resulteert tot:

[cut crap]

Nee jongeman, dit lijkt nergens op. Je begon nochtans goed (afgezien van die verschrijving).

Als je links een factor 4^x buiten haakjes haalt en rechts een factor 3^x buiten haakjes haalt dan krijg je

4^x(1 − 4⁻¹) = 3^x(3 − 1)

Nu mag je eens even gaan nadenken hoe je verder kunt gaan.

Super-B, als ik jou was zou ik eens gaan inversteren in bijles of een cursus. Want je mist gewoon zoveel basiskennis. Ik weet niet welke studie je doet, maar als je zo door gaat vrees ik het ergste voor je.

"Verschuif de lijn m over de vector p = OP→ en noem de verschoven lijn l."

Wat wordt bedoeld met verschuiven? Alleen in x/y richting verschuiven? Of ook z?.

quote:

Op zaterdag 13 september 2014 21:28 schreef Super-B het volgende:

[..]

Bedankt voor de tip, maar ik vind het tot nu toe vrij goed te doen met zelfstudie en dit topic.

Gelukkig behoren de vragen die ik stel tot de stof van het tentamen voor volgende week en behoren ze volgens het boek tot 'harder problems'. De basic-opgaven gaan mij wel makkelijk af. Echter is er nog veel werk te doen om de kennis goed te beheersen, maar ik denk dat het tentamen wel te doen is.

De stof van het (deel)tentamen is het volgende:

[ afbeelding ]

De onderwerpen die ik tot nu toe nog wel pittig vind zijn:

-Logartime (niet de regels, maar de wat moeilijkere opgaven met log, ln en/of het getal e)
-Polynomen en staartdelingen.
-Afgeleiden (nieuwe materie voor mij)
-Regels voor differentiëren (ook nieuwe materie voor mij).

Inverse functies en samengestelde functies zijn ook nieuw voor mij, echter begrijp ik het tot dusverre wel.

Voor velen in dit topic is dit een eitje en zullen mijn vragen dan ook niet de moeilijkste zijn, maar het gaat tot nu toe wel goed met leren (met hier en daar nog wat slordigheidsfoutjes en wat fouten waaraan te zien is dat ik het nog niet goed beheers).

Onzin, je hebt voor de zomervakantie een paar maanden lang allemaal vragen gepost over differentiëren. Weet je nog, met de ketting/product/som/quotiëntregel?

quote:

Op zaterdag 13 september 2014 21:13 schreef Novermars het volgende:
Super-B, als ik jou was zou ik eens gaan inversteren in bijles of een cursus. Want je mist gewoon zoveel basiskennis. Ik weet niet welke studie je doet, maar als je zo door gaat vrees ik het ergste voor je.

Riparius had hem ook al verteld dat hij de Spijkerreeks moet kopen, een tijd terug, of dat was tegen een andere hbo'er die ook economie wilde gaan doen. Anyhow, dat heeft diegene ook niet gedaan.

quote:

Op zaterdag 13 september 2014 23:25 schreef netchip het volgende:
"Verschuif de lijn m over de vector p = OP→ en noem de verschoven lijn l."

Wat wordt bedoeld met verschuiven? Alleen in x/y richting verschuiven? Of ook z?.

Iets meer context?

quote:

Op zaterdag 13 september 2014 23:25 schreef netchip het volgende:
"Verschuif de lijn m over de vector p = OP→ en noem de verschoven lijn l."

Wat wordt bedoeld met verschuiven? Alleen in x/y richting verschuiven? Of ook z?.

Een vector is een gericht lijnstuk (of een equivalentieklasse van gerichte lijnstukken met dezelfde lengte en dezelfde richting) en een vector definieert aldus een translatie. Als je niet vertelt welke vector je vector p = OP is, dan is je vraag ook niet te beantwoorden.

quote:

Op zaterdag 13 september 2014 23:41 schreef Novermars het volgende:

[..]

Iets meer context?

quote:

Op zaterdag 13 september 2014 23:41 schreef Riparius het volgende:

[..]

Een vector is een gericht lijnstuk (of een equivalentieklasse van gerichte lijnstukken met dezelfde lengte en dezelfde richting) en een vector definieert aldus een translatie. Als je niet vertelt welke vector je vector p = OP is, dan is je vraag ook niet te beantwoorden.

Paragraaf 1.2: http://www.staff.science.(...)inalg2013dictaat.pdf

quote:

Op zaterdag 13 september 2014 23:44 schreef netchip het volgende:

[..]

[..]

Paragraaf 1.2: http://www.staff.science.(...)inalg2013dictaat.pdf

Zoals ik het interpreteer in alle dimensies. De verzameling moet je zien als alle evenwijdige lijnen van de vector .

quote:

Op zaterdag 13 september 2014 23:48 schreef Novermars het volgende:

[..]

Zoals ik het interpreteer in alle dimensies. De verzameling moet je zien als alle evenwijdige lijnen van de vector .

OK, dus als je een voorbeeld maakt, zou het er zo uit kunnen zien? https://www.dropbox.com/s(...)oorstelling.png?dl=0

quote:

Op zaterdag 13 september 2014 23:44 schreef netchip het volgende:

[..]

[..]

Paragraaf 1.2: http://www.staff.science.(...)inalg2013dictaat.pdf

Teken gewoon eens een plaatje, in een plat vlak om het simpel te houden. Kies een punt O (als oorsprong) en een punt A ≠ O en teken vector OA = a, dan is elk punt op de rechte door O en A het eindpunt van een vector v = λa voor een zekere λ ∈ R, en als je λ de verzameling R van alle reële getallen laat doorlopen dan krijg je voor het eindpunt van vector v = λa elk punt op de rechte door O en A. We noemen v = λa daarom een vectorvoorstelling van de rechte m door O en A.

Kies vervolgens een willekeurig punt P buiten lijn m en verschuif lijn m dan in één rechte beweging zodanig dat punt O op lijn m in punt P komt te liggen. Dan hebben we als beeld van de rechte lijn m een rechte lijn l door punt P die evenwijdig is aan lijn m. Elk punt op deze lijn l is nu het eindpunt van een vector v = p + λa voor een zekere λ ∈ R, en als je λ weer de verzameling R van alle reële getallen laat doorlopen dan krijg je als eindpunt van vector v = p + λa elk punt op de rechte l door P evenwijdig aan m. Aldus is v = p + λa een vectorvoorstelling van l. Vector a heet een richtingsvector van lijn l en vector p heet een steunvector (ook wel een plaatsvector) van lijn l.

quote:

Op zondag 14 september 2014 15:17 schreef Super-B het volgende:
[ afbeelding ]

Als ik (e^0,001 - 1) / 1 invul in mijn rekenmachine krijg ik geen [ afbeelding ], maar 0,0010005 Doe ik iets fout of..?

Je deelt door 1 ipv x.

quote:

Op zondag 14 september 2014 15:17 schreef Super-B het volgende:
[ afbeelding ]

Als ik (e^0,001 - 1) / 1 invul in mijn rekenmachine krijg ik geen [ afbeelding ], maar 0,0010005 Doe ik iets fout of..?

Ja, je doet iets fout, en in mijn glazen bol zie ik dat je waarschijnlijk alleen e^x − 1 hebt berekend voor x = 0,001. Je bent dus helemaal vergeten dat je het resultaat weer door x moest delen.

quote:

Op zondag 14 september 2014 15:26 schreef Super-B het volgende:

[..]

[..]

Wiskunde is echt een heerlijk vak, met name door de uitdaging die er in zit.

Hopelijk zie je ook waarom die limiet van (e^x − 1)/x voor x → 0 oftewel de limiet van (e^h − 1)/h voor h → 0 nu zo interessant is. Als je de afgeleide gaat bepalen van

f(x) = a^x

voor een a ∈ R⁺ met behulp van de definitie van de afgeleide, dan krijg je

f'(x) = lim_h→0 (a^x+h − a^x)/h

en aangezien a^x+h = a^x·a^h kunnen we een factor a^x buiten haakjes halen in de teller van het differentiequotiënt en omdat a^x niet afhangt van h kunnen we deze factor a^x voor de limiet brengen zodat we kunnen schrijven

f'(x) = a^x · lim_h→0 (a^h − 1)/h

Maar omdat 1 = a⁰ is lim_h→0 (a^h − 1)/h = lim_h→0 (a^h − a⁰)/h niets anders dan de afgeleide van de functie in het punt x = 0 oftewel f'(0). We vinden voor de functie f(x) = a^x dus

f'(x) = f'(0)·a^x

Een exponentiële functie heeft dus een afgeleide die weer een exponentiële functie is met datzelfde grondtal, maar dan wel vermenigvuldigd met een constante factor die de steilheid geeft van de grafiek van de functie bij x = 0. En nu blijkt er precies één positief reëel getal a te zijn waarbij de steilheid van de exponentiële curve bij x = 0 precies gelijk is aan 1, en dat getal noemen we e. Voor a = e heb je zo dus

f'(x) = e^x

als afgeleide van

f(x) = e^x

Natuurlijk wil je nu ook nog weten wat die f'(0) = lim_h→0 (a^h − 1)/h voor een willekeurige (positieve, reële) a nu in het algemeen voorstelt, en dat blijkt niets anders te zijn dan de natuurlijke logaritme van a, dus

lim_h→0 (a^h − 1)/h = ln a

Zo hebben we dus voor

f(x) = a^x

met a ∈ R⁺ in het algemeen als afgeleide

f'(x) = a^x·ln a

Okay volgens mij is dit redelijk simpel maar ik zie het gewoon niet, ik hoop dat iemand mij kan helpen.

Is de som: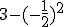 hetzelfde als: ?
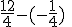Naar mijn inzien namelijk wel maar de antwoorden verschillen. het antwoord van som 1 is namelijk 2,75 en die van som twee 3,25.

quote:

Op zondag 14 september 2014 16:08 schreef nokenindekoken het volgende:
Okay volgens mij is dit redelijk simpel maar ik zie het gewoon niet, ik hoop dat iemand mij kan helpen.

Is de som: hetzelfde als: ?
Naar mijn inzien namelijk wel maar de antwoorden verschillen. het antwoord van som 1 is namelijk 2,75 en die van som twee 3,25.

Nee, dit is niet hetzelfde. Je negeert namelijk de rekenregel min maal min geeft plus. Het kwadraat van −½ is ¼, niet −¼.