SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



bereken de odds ratio dan voor X=0quote:Op maandag 25 juni 2012 18:40 schreef Soldier2000 het volgende:
[..]
Ik ben opzoek naar de algemene betekenis van constant
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je hoeft toch helemaal niets te berekenen om te weten wat de waarde constant wil zeggen in de bovenstaande tabel? Ik heb de data set namelijk niet.quote:
The response to the test mailing = -3.648 when X (M, R, F etc.) =0 ?
Is het niet zo dat de constante waarde wel onderdeel van de formule is, maar geen interpreteerbare betekenis heeft?
[ Bericht 12% gewijzigd door Soldier2000 op 25-06-2012 20:41:07 ]
BlaBlaBla


Nee, bereken de odds ratio symbolisch.quote:Op maandag 25 juni 2012 20:12 schreef Soldier2000 het volgende:
[..]
Is het niet zo dat de constante waarde wel onderdeel van de formule is, maar geen interpreteerbare betekenis heeft?dan weet ik namelijk al voldoende
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Het klinkt zo gemakkelijk, maar mijn statistiek is zo snel zo ver weggezaktquote:Op maandag 25 juni 2012 20:44 schreef GlowMouse het volgende:
[..]
Nee, bereken de odds ratio symbolisch.
BlaBlaBla


Dadelijk even m'n vorige vraag terug zoeken, m'n internet lag er een aantal dagen uit. Voor nu even een nieuwe vraag, maar zie me als een investering - wanneer mijn kennis op niveau is kom ik hier helpen.
Hoe bereken ik arctan (3/4) uit m'n hoofd? Een sinus of cosinus is gesneden koek, maar de tangens ligt me wat minder lekker.
Hoe bereken ik arctan (3/4) uit m'n hoofd? Een sinus of cosinus is gesneden koek, maar de tangens ligt me wat minder lekker.
"Social order at the expense of liberty is hardly a bargain."


Wolfram alpha geeft geen exact antwoord (dus die zal niet bestaan of vrij gecompliceerd zijn), dus je zult het dan moeten benaderen net zoals je rekenmachine dat doet. Je kan hiervoor een Taylorreeks gebruiken... die van de arctan convergeert heel snel dus na een aantal termen ben je wel klaar (vooral als x dichtbij 0 zit).quote:Op maandag 25 juni 2012 22:19 schreef Quir het volgende:
Dadelijk even m'n vorige vraag terug zoeken, m'n internet lag er een aantal dagen uit. Voor nu even een nieuwe vraag, maar zie me als een investering - wanneer mijn kennis op niveau is kom ik hier helpen.
Hoe bereken ik arctan (3/4) uit m'n hoofd? Een sinus of cosinus is gesneden koek, maar de tangens ligt me wat minder lekker.
Die snelle benadering geeft al arctan(3/4) = 0.656 terwijl het eigenlijk 0.643 is.
Sommige waarden kan je wel makkelijk exact berekenen, zoals arctan(1) of arctan(0) (probeer maar).


Ah, zo - nouja, de vraag in het boek was arccos(-arctan(3/4)), maar ik probeerde de bijbehorende hoek te vinden. Als dat niet zo makkelijk gaat, dan laat ik 't mooi zitten. En arctan 1 of 0 had ik al door ((pi/4) en 0). Dank voor je antwoord.
"Social order at the expense of liberty is hardly a bargain."


Misschien kan onze gonio-vriend Riparius je beter helpenquote:Op maandag 25 juni 2012 22:55 schreef Quir het volgende:
Ah, zo - nouja, de vraag in het boek was arccos(-arctan(3/4)), maar ik probeerde de bijbehorende hoek te vinden. Als dat niet zo makkelijk gaat, dan laat ik 't mooi zitten. En arctan 1 of 0 had ik al door ((pi/4) en 0). Dank voor je antwoord.


Weet je zeker dat er niet naar cos(-arctan(3/4)) wordt gevraagd?quote:Op maandag 25 juni 2012 22:55 schreef Quir het volgende:
Ah, zo - nouja, de vraag in het boek was arccos(-arctan(3/4)), maar ik probeerde de bijbehorende hoek te vinden. Als dat niet zo makkelijk gaat, dan laat ik 't mooi zitten. En arctan 1 of 0 had ik al door ((pi/4) en 0). Dank voor je antwoord.


Gevraagd om te berekenen:
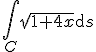 met C een curve in
met C een curve in 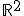 en
en 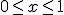 ,
, 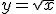
Mijn berekening:
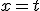 ,
, 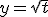 dus
dus 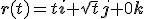 en dus
en dus 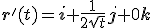
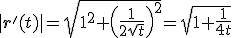
dus de integraal wordt: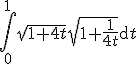
Klopt dit tot hier?
Mijn berekening:
dus de integraal wordt:
Klopt dit tot hier?


Ja, maar je maakt het jezelf onnodig moeilijk. Je heb namelijk:quote:Op dinsdag 26 juni 2012 00:22 schreef Dale. het volgende:
Gevraagd om te berekenen:met C een curve in
en
,
Mijn berekening:,
dus
en dus
dus de integraal wordt:
Klopt dit tot hier?
ds = (dx2 + dy2)1/2 = (1 + (dy/dx)2)1/2∙dx
en aangezien dy/dx = ½∙x-1/2 krijg je dan meteen de integraal die je geeft, maar dan met x als variabele.


Oke de integraal klopt dus. Maar dan hoe reken ik deze uit? Wolfram geeft http://www.wolframalpha.com/input/?i=int+sqrt%281+%2B+4*t%29+*+sqrt%281+%2B+1%2F%284*t%29%29+dt maar daar begrijp ik de stap niet van 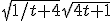 naar
naar 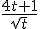 niet. De integraal moet simpeler op te lossen zijn toch ook trouwens?
niet. De integraal moet simpeler op te lossen zijn toch ook trouwens?


Het is beter om gebruik te maken van:quote:Op maandag 25 juni 2012 22:30 schreef thenxero het volgende:
[..]
Wolfram alpha geeft geen exact antwoord (dus die zal niet bestaan of vrij gecompliceerd zijn), dus je zult het dan moeten benaderen net zoals je rekenmachine dat doet. Je kan hiervoor een Taylorreeks gebruiken... die van de arctan convergeert heel snel dus na een aantal termen ben je wel klaar (vooral als x dichtbij 0 zit).
Die snelle benadering geeft al arctan(3/4) = 0.656 terwijl het eigenlijk 0.643 is.
Sommige waarden kan je wel makkelijk exact berekenen, zoals arctan(1) of arctan(0) (probeer maar).
arctan(3/4) = 2∙arctan(1/3)
aangezien de reeks (zoals je zelf opmerkt) sneller convergeert naarmate x dichter bij 0 ligt.
Dan krijg je:
arctan(3/4) ≈ 2∙(1/3 - (1/3)3/3 + (1/3)5/5) = 782/1215 = 0,6436 ...
Nog veel beter wordt het als je gebruik maakt van
arctan(3/4) = π/4 - arctan(1/7)
Aangezien we niet eerst een benadering voor π uit willen rekenen (waarvoor we ook weer een reeksontwikkeling nodig zouden hebben) maken we hiervoor gebruik van de benadering 355/113 (het getal van Metius). Dan krijgen we:
arctan(3/4) ≈ (1/4)∙(355/113) - (1/7 - (1/7)3/3 + (1/7)5/5) = 0,643501...
En zie daar, we hebben arctan(3/4) in zes decimalen nauwkeurig.
[ Bericht 15% gewijzigd door Riparius op 26-06-2012 03:32:50 ]


Je moet niet meteen je probleem in WolframAlpha (of een ander computeralgebra systeem) stoppen en dan proberen dat slaafs na te doen met pen en papier. Een mens is nog altijd creatiever dan een computer (maar jij kennelijk niet ...).quote:Op dinsdag 26 juni 2012 00:45 schreef Dale. het volgende:
Oke de integraal klopt dus. Maar dan hoe reken ik deze uit? Wolfram geeft http://www.wolframalpha.com/input/?i=int+sqrt%281+%2B+4*t%29+*+sqrt%281+%2B+1%2F%284*t%29%29+dt maar daar begrijp ik de stap niet vannaar
niet. De integraal moet simpeler op te lossen zijn toch ook trouwens?
Ik ga eerst je integrand in een wat hanteerbaarder vorm brengen. We hebben:
√(1 + 4t)∙√(1 + 1/(4t)) = √(1 + 1/(4t) + 4t + 1) = √(4t + 2 + 1/(4t))
Nu gaan we de termen onder het wortelteken onder één noemer brengen. Dit geeft:
4t + 2 + 1/(4t) = (16t2 + 8t + 1)/(4t) = (4t + 1)2/(4t)
Dus krijgen we:
√(4t + 2 + 1/(4t)) = (4t + 1)∙(4t)-1/2 = ½∙(4t + 1)∙t-1/2 = 2∙t1/2 + ½∙t-1/2
De integraal wordt nu:
∫01 (2∙t1/2 + ½∙t-1/2)∙dt = [(4/3)∙t3/2 + t1/2]01 = 4/3 + 1 = 7/3.
[ Bericht 0% gewijzigd door Riparius op 26-06-2012 02:33:30 ]


Volgens mij zou het rekenmachine het ook niet eens zijn met arccos(-arctan(3/4)), dus, ja, het moest inderdaad cos zijn. Foutje.quote:Op dinsdag 26 juni 2012 00:05 schreef Riparius het volgende:
[..]
Weet je zeker dat er niet naar cos(-arctan(3/4)) wordt gevraagd?
"Social order at the expense of liberty is hardly a bargain."


Je begrijpt er kennelijk nog niet veel van, want -arctan(3/4) ligt tussen -π/4 en 0 en daarmee binnen het domein [-1,1] van de (reële) arcus cosinus functie, zodat arccos(-arctan(3/4)) gewoon (numeriek) is te bepalen.quote:Op dinsdag 26 juni 2012 11:50 schreef Quir het volgende:
[..]
Volgens mij zou de rekenmachine het ook niet eens zijn met arccos(-arctan(3/4)), dus, ja, het moest inderdaad cos zijn. Foutje.
Maar goed, het ging dus om cos(-arctan(3/4)).
Laten we zeggen dat
arctan(3/4) = α,
dan is
tan α = 3/4, met -½π < α < ½π
Nu maken we gebruik van de identiteit
1 + tan2α = sec2α,
waarvoor we uiteraard ook kunnen schrijven
1 + tan2α = 1/cos2α
We weten dat tan α = 3/4, dus hebben we
1/cos2α = 1 + (3/4)2 = 25/16,
en dus
cos2α = 16/25
Nu hebben we ook -½π < α < ½π en dus is cos α > 0, zodat we vinden
cos α = 4/5
De cosinusfunctie is een even functie, en dus is ook
cos(-α) = 4/5
En aangezien arctan(3/4) = α heb je dus:
cos(-arctan(3/4)) = cos(-α) = 4/5.
Voila.
Je zou ook een plaatje kunnen tekenen, en dan zie je dat je te maken hebt met een rechthoekige driehoek waarvan de zijden zich verhouden als 3 : 4 : 5 aangezien tan α = 3/4 gelijk is aan de overstaande rechthoekszijde gedeeld door de aanliggende rechthoekszijde van hoek α. En aangezien de cosinus van deze hoek gelijk is aan de aanliggende rechthoekszijde gedeeld door de schuine zijde, weet je dan direct dat cos α = 4/5.
[ Bericht 5% gewijzigd door Riparius op 26-06-2012 14:02:15 ]


Pagina 149 zegt [0, pi] en daar ligt -arctan(3/4) voor zover ik weet niet in. Als ik danwel 't boek iets fout heeft hoor ik het graag.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt."Social order at the expense of liberty is hardly a bargain."


En ohja, sec ben ik nog niet tegengekomen in 't boek, maar de rest wel. Ik volg het verder, dank!
"Social order at the expense of liberty is hardly a bargain."


quote:Op dinsdag 26 juni 2012 12:35 schreef Quir het volgende:
Pagina 149 zegt [0, pi] en daar ligt -arctan(3/4) voor zover ik weet niet in. Als ik danwel 't boek iets fout heeft hoor ik het graag.Nee, je begrijpt het niet. Het pleit ook niet voor je dat je kennelijk meer vertrouwen hebt in een - foutief - gebruik van je rekenmachine dan in mijn uitleg. Ik vermoed dat je je rekenmachine op graden hebt laten staan in plaats van op radialen, en dan is het nogal wiedes dat de machine je invoer niet accepteert. Dit is weer typisch zo'n hersenloos gebruik van een calculator.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Je hebt -½π < arctan(x) < ½π voor elke reële x, en arctan(0) = 0 en arctan(1) = ¼π. De arcus tangens functie is strict monotoon stijgend zodat arctan(0) < arctan(¾) < arctan(1) en dus 0 < arctan(¾) < ¼π en dus -¼π < -arctan(¾) < 0. En aangezien 0 < π < 4 is dus -1 < -¼π < 0 en daarmee -1 < -arctan(¾) < 0.
[ Bericht 14% gewijzigd door Riparius op 26-06-2012 14:56:31 ]


Ik had dus een paar uur geleden m'n wiskunde mondeling.
1. casus, wat eenvoudige goniometrie, raaklijnen en integralen. Op her en der een haakje en een k*2π na foutloos.
2. meetkunde: totaal verneukt (zoals iedereen)
3. wentelen, piece of cake.,
3. logaritmen. peanuts
4. optimaliseren, slordig begonnen, na een vermaning foutloos.
5. Mijn klok! Kreeg wat historische vragen(hij gaf toe dat mijn kennis van de wiskundige historie verder was dan de zijne)
6. Mercatorprojectie. Hij was onder de indruk, ondanks de geringe hoeveelheid tijd kreeg ik toch nog een vraag over poolcoördinaten. Mijn werkstuk is daarna ingenomen voor nadere observatie (hij wilde wel even kijken wat ik van deze 'hogere' wiskunde bakte.
Rip, bedankt!
1. casus, wat eenvoudige goniometrie, raaklijnen en integralen. Op her en der een haakje en een k*2π na foutloos.
2. meetkunde: totaal verneukt (zoals iedereen)
3. wentelen, piece of cake.,
3. logaritmen. peanuts
4. optimaliseren, slordig begonnen, na een vermaning foutloos.
5. Mijn klok! Kreeg wat historische vragen(hij gaf toe dat mijn kennis van de wiskundige historie verder was dan de zijne)
6. Mercatorprojectie. Hij was onder de indruk, ondanks de geringe hoeveelheid tijd kreeg ik toch nog een vraag over poolcoördinaten. Mijn werkstuk is daarna ingenomen voor nadere observatie (hij wilde wel even kijken wat ik van deze 'hogere' wiskunde bakte.
Rip, bedankt!
Fervent tegenstander van het korps lasergamers.


Graag gedaan. Maar wat hielden die meetkunde opgaven in?quote:Op dinsdag 26 juni 2012 14:50 schreef Amoeba het volgende:
Ik had dus een paar uur geleden m'n wiskunde mondeling.
1. casus, wat eenvoudige goniometrie, raaklijnen en integralen. Op her en der een haakje en een k*2π na foutloos.
2. meetkunde: totaal verneukt (zoals iedereen)
3. wentelen, piece of cake.,
3. logaritmen. peanuts
4. optimaliseren, slordig begonnen, na een vermaning foutloos.
5. Mijn klok! Kreeg wat historische vragen(hij gaf toe dat mijn kennis van de wiskundige historie verder was dan de zijne)
6. Mercatorprojectie. Hij was onder de indruk, ondanks de geringe hoeveelheid tijd kreeg ik toch nog een vraag over poolcoördinaten. Mijn werkstuk is daarna ingenomen voor nadere observatie (hij wilde wel even kijken wat ik van deze 'hogere' wiskunde bakte.
Rip, bedankt!
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |

