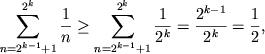WFL Wetenschap, Filosofie, Levensbeschouwing
Discussieer hier over alle aspecten van de wetenschap, filosofische problemen en zaken van levensbeschouwelijke aard.



Ah, jij bent al verder gekomen dan ik met het uitproberen dan ik. Voorlopig ben ik bij deze vraag enkel tot de conclusie gekomen dat het een goede keuze van me is geweest om geen experimenteel wetenschapper te worden.quote:Op donderdag 8 december 2005 17:42 schreef ATuin-hek het volgende:
met een ijsklontje uitgeprobeerd in de magnetron lijkt 4 A te zijn


Maar hoe corrigeren je hersenen dat? Misschien wel door je ogen te draaien!quote:Op woensdag 7 december 2005 23:32 schreef Quarks het volgende:
[..]
Dat ook, maar het gaat hier om het beeld wat schijnbaar door je hersenen wordt gecorrigeerd zodat het lijkt alsof je je hoofd recht houdt.


Je ogen draaien ook wel gedeeltelijk me;, zo'n 10 tot 20 graden.quote:Op donderdag 8 december 2005 19:00 schreef thabit het volgende:
[..]
Maar hoe corrigeren je hersenen dat? Misschien wel door je ogen te draaien!
* 11:15, restate my assumptions: 1. Mathematics is the language of nature. 2. Everything around us can be represented and understood through numbers. 3. If you graph these numbers, patterns emerge. Therefore: There are patterns everywhere in nature.*


Vraag 7: kan water branden?
Water kan geoxideerd worden tot H2O2. Maar voor de twee mogelijkheden die gegeven worden kan ik geen bron vinden:
- zeer hoge druk, zeer hoge T, voldoende O2: kan zich hier een evenwichtstoestand voordoen? Blijkbaar niet want de ontbinding van H2O2 is een exotherme reactie. Vanaf een temp van 70°C kan H2O2 damp detoneren, hoge temperaturen zijn dus niet gewenst, en aangezien een detonatie propageert via een drukgolf zullen hoge drukken ook niet echt helpen (?)
- zeer lage druk en voldoende CO2: Planten produceren H2O2, maar bij hoge concentraties van CO2 stopt de productie. Mogelijk dat in een water - koolzuur mengsel onder invloed van zonlicht vrije radicalen gevormd kunnen worden die reageren tot waterstofperoxide?
Water kan geoxideerd worden tot H2O2. Maar voor de twee mogelijkheden die gegeven worden kan ik geen bron vinden:
- zeer hoge druk, zeer hoge T, voldoende O2: kan zich hier een evenwichtstoestand voordoen? Blijkbaar niet want de ontbinding van H2O2 is een exotherme reactie. Vanaf een temp van 70°C kan H2O2 damp detoneren, hoge temperaturen zijn dus niet gewenst, en aangezien een detonatie propageert via een drukgolf zullen hoge drukken ook niet echt helpen (?)
- zeer lage druk en voldoende CO2: Planten produceren H2O2, maar bij hoge concentraties van CO2 stopt de productie. Mogelijk dat in een water - koolzuur mengsel onder invloed van zonlicht vrije radicalen gevormd kunnen worden die reageren tot waterstofperoxide?


Verrek, effe voor de spiegel getest, het is nog waar ook!quote:Op donderdag 8 december 2005 19:25 schreef Quarks het volgende:
[..]
Je ogen draaien ook wel gedeeltelijk me;, zo'n 10 tot 20 graden.


Experiment uitgevoerd. Vraag 4 is, zoals de theorie al voorspelde, inderdaad A.quote:Op donderdag 8 december 2005 18:33 schreef thabit het volgende:
[..]
Ah, jij bent al verder gekomen dan ik met het uitproberen dan ik. Voorlopig ben ik bij deze vraag enkel tot de conclusie gekomen dat het een goede keuze van me is geweest om geen experimenteel wetenschapper te worden.


Ik weet niet of maïzena dezelfde eigenschappen heeft als custard, maar ook ik heb beelden gezien dat iemand over een zwembad vol water/custard loopt. ik gok dus op A.
Aldus.


Die proef is een keer gedaan bij het programma Hoe?Zo! Wel leuk om te zienquote:Op donderdag 8 december 2005 20:44 schreef Z het volgende:
Ik weet niet of maïzena dezelfde eigenschappen heeft als custard, maar ook ik heb beelden gezien dat iemand over een zwembad vol water/custard loopt. ik gok dus op A.
"Pain is my friend. I can trust pain. I can trust pain to make my life utterly miserable."
"My brain is too smart for me."
"We don't need no education." "Yes you do, you just used a double negative."
"My brain is too smart for me."
"We don't need no education." "Yes you do, you just used a double negative."


Met die bezemsteel heb ik zelf het experiment uitgevoerd, het antwoord is C
ook wel logisch want de steel wordt door het gewicht van de bezem steviger op de vinger die er dicht bij is gedrukt. Welke vinger ik ook bewoog, de steel bleef stil liggen op de vinger die het dichtst bij de bezem was.
ook wel logisch want de steel wordt door het gewicht van de bezem steviger op de vinger die er dicht bij is gedrukt. Welke vinger ik ook bewoog, de steel bleef stil liggen op de vinger die het dichtst bij de bezem was.
Glimlach, morgen is het erger!


Lees de vraag eens goed. Er staat duidelijk "bezemsteel" en niet "bezem".quote:Op vrijdag 9 december 2005 23:04 schreef janfreak het volgende:
Met die bezemsteel heb ik zelf het experiment uitgevoerd, het antwoord is C
ook wel logisch want de steel wordt door het gewicht van de bezem steviger op de vinger die er dicht bij is gedrukt. Welke vinger ik ook bewoog, de steel bleef stil liggen op de vinger die het dichtst bij de bezem was.


Dan B, want gezichtsbedrog is het zeker niet.quote:Op maandag 12 december 2005 16:36 schreef Goldboy het volgende:
Persoonlijk twijfel ik nog over 14. Het is of b, of C.
Iemand nog geprobeerd?
Argh, vergeten!quote:Op maandag 12 december 2005 16:38 schreef thabit het volgende:
Je bent een beetje te laat. De deadline voor het insturen was vandaag om 12 uur. .
* 11:15, restate my assumptions: 1. Mathematics is the language of nature. 2. Everything around us can be represented and understood through numbers. 3. If you graph these numbers, patterns emerge. Therefore: There are patterns everywhere in nature.*


Insturen? Hoezo? Kon je er iets mee winnen dan?quote:Op maandag 12 december 2005 16:38 schreef thabit het volgende:
Je bent een beetje te laat. De deadline voor het insturen was vandaag om 12 uur. .


Dit zijn de antwoorden die ik heb ingestuurd. Ik heb er een paar gegokt, dus ik verwacht niet dat ze allemaal goed zijn. Maar wie weet zit er een kansje in.
1C 2A 3A 4A 5C 6A 7A 8B 9C 10B 11B 12B 13A 14B 15C 16C 17C 18B 19A 20C
1C 2A 3A 4A 5C 6A 7A 8B 9C 10B 11B 12B 13A 14B 15C 16C 17C 18B 19A 20C


Kun je 15 uitleggen?quote:Op maandag 12 december 2005 16:55 schreef thabit het volgende:
Dit zijn de antwoorden die ik heb ingestuurd. Ik heb er een paar gegokt, dus ik verwacht niet dat ze allemaal goed zijn. Maar wie weet zit er een kansje in.
1C 2A 3A 4A 5C 6A 7A 8B 9C 10B 11B 12B 13A 14B 15C 16C 17C 18B 19A 20C
Ik dacht dat het ruikende deel van je neus vrij hoog in je neusholte zit.
* 11:15, restate my assumptions: 1. Mathematics is the language of nature. 2. Everything around us can be represented and understood through numbers. 3. If you graph these numbers, patterns emerge. Therefore: There are patterns everywhere in nature.*


Mij lijkt A of B ook waarschijnlijker.quote:Op maandag 12 december 2005 17:02 schreef Quarks het volgende:
[..]
Kun je 15 uitleggen?
Ik dacht dat het ruikende deel van je neus vrij hoog in je neusholte zit.


Ik had op internet iets gevonden wat vrij vaag was, maar wel het meest op C lijkt. Grofweg kwam het erop neer dat je door te snuffelen bepaalde reukcentra in de hersenen actief maakt. Het was onderzoek gedaan in Berkeley, dus wel vrij serieus te nemen.


Ik had dit gevonden:quote:Op maandag 12 december 2005 17:38 schreef thabit het volgende:
Ik had op internet iets gevonden wat vrij vaag was, maar wel het meest op C lijkt. Grofweg kwam het erop neer dat je door te snuffelen bepaalde reukcentra in de hersenen actief maakt. Het was onderzoek gedaan in Berkeley, dus wel vrij serieus te nemen.
quote:Tijdens de normale ademhaling bereikt de inademingslucht de bovenste neusgang, waar het reukepitheel zich bevindt. De daar aangekomen lucht is door het bloed en vochtrijke neusslijmvlies voorverwarmd, vochtig gemaakt en van veel stofdeeltjes gezuiverd. Als men beter wil ruiken, gaat men snuffelen, waardoor de dan snel in- en uitgeademde lucht de bovenste neusgang beter kan bereiken. Door het snel op elkaar volgen van reukprikkels wordt de geurgewaarwording versterkt. Het reukzintuig kan ook worden gestimuleerd via de tongbewegingen, waarbij de lucht uit de mond via de achterzijde (neuskeelholte) omhoog wordt gestuwd naar het reukepitheel. De `smaak’ van het voedsel berust voor een belangrijk deel op geurgewaarwordingen die op deze wijze tot stand komen; bij verlies van de reuk is de smaak sterk verminderd. Het aantal door de mens waar te nemen geuren wordt geschat op 200.000.
* 11:15, restate my assumptions: 1. Mathematics is the language of nature. 2. Everything around us can be represented and understood through numbers. 3. If you graph these numbers, patterns emerge. Therefore: There are patterns everywhere in nature.*


Ah, maar waarom doen we dan korte ademteugjes bij het snuffelen in plaats van 1 lange stevige?quote:


Er staat: Door het snel op elkaar volgen van reukprikkels wordt de geurgewaarwording versterkt.quote:Op maandag 12 december 2005 18:20 schreef thabit het volgende:
[..]
Ah, maar waarom doen we dan korte ademteugjes bij het snuffelen in plaats van 1 lange stevige?
* 11:15, restate my assumptions: 1. Mathematics is the language of nature. 2. Everything around us can be represented and understood through numbers. 3. If you graph these numbers, patterns emerge. Therefore: There are patterns everywhere in nature.*


Dus toch antwoord C? .quote:Op maandag 12 december 2005 18:40 schreef Quarks het volgende:
[..]
Er staat: Door het snel op elkaar volgen van reukprikkels wordt de geurgewaarwording versterkt.
Nou ja, de deadline is al voorbij dus discussieren heeft weinig zin meer. .


Deze berekening klopt volgens mij niet. Buiten dat alle x1,-2 -3 en niet te volgen zijn zonder tekening,quote:Op dinsdag 29 november 2005 18:31 schreef Quarks het volgende:
[..]
Je kunt het zwaartepunt beïnvloeden met je tegels.
Door meer tegels als contragewicht te gebruiken verleg je je zwaartepunt.
[afbeelding]
Uitleg:
We noemen de bovenste tegel T1, en de tegel daaronder T2, enzovoorts. We laten de toren naar rechts overhellen.
Hoeveel kan T1 uitsteken t.o.v. T2 zodat T1 precies in evenwicht hangt?
We noemen de breedte van de tegel d. Het gedeelte wat T1 links uitsteekt t.o.v. van zijn draaipunt op T2 noemen we X1. Het gedeelte wat T1 rechts uitsteekt t.o.v. zijn draaipunt op T2 noemen we d-X1. De massa van de tegel doet niet terzake en laten we dus weg. Ook de zwaartekrachtversnelling laten we weg omdat die niet van invloed is behalve dat hij in werkelijkheid aanwezig moet zijn.
De Momenten links en rechts van het draaipunt (dat op d-X1 ligt) moeten gelijk zijn. Omdat de tegel een homogene massa is die niet dikker of dunner naarmate je meer naar buiten of binnen komt, kunnen we alle massa veronderstellen aanwezig te zijn in het punt 0,5 d respectievelijk 0,5 (d-X1).
Het Moment links wordt daarmee: 0,5 x X1. Het Moment rechts wordt zo 0,5 (d-X1). De Momenten zijn gelijk omdat de zaak in evenwicht hangt, waaruit volgt X1 = 0,5 d. Tegel T1 steekt X1-d uit, dus T1 steekt 1/2 tegel uit t.o.v. de onderliggende tegel T2.
Hoeveel kan T2 uitsteken t.o.v. T3 zodat T2 precies in evenwicht hangt (met T1 nog aanwezig)?
Ook hier geldt weer dat de Momenten links en rechts van het draaipunt, dat op d-X2 ligt, gelijk moeten zijn.
Het Moment links van het draaipunt: 0,5 x X2. Het Moment rechts van het draaipunt bestaat nu evenwel uit twee componenten, te weten voortvloeiend uit T2 én voortvloeiend uit T1. Beiden moeten bij elkaar worden opgeteld en gelijk zijn aan het Moment links. De eerste component is 0,5 x (d-X2). De tweede component, namelijk de bijdrage van T1, is: 0,5 x (d-X2). Omdat T1 precies in evenwicht ligt mag alle massa worden verondersteld in één punt te liggen, nl. het draaipunt van T1 op T2.
Links en rechts zijn gelijk dus 0,5 x X2 = 0,5 x (d-X2) + (d-X2). Oftewel 4 X2 = 3 d, en X2 = 0,75 d. Tegel T2 steekt dus 1/4 tegel uit t.o.v. de onderliggende tegel T3.
Totaal steekt de toren nu uit 1/2 + 1/4 = 0,75 tegel.
Hoeveel kan T3 uitsteken t.o.v. T4 zodat T3 precies in evenwicht hangt (met T1 en T2 nog aanwezig)?
Er geldt weer hetzelfde als boven, echter nu liggen er twee tegels bovenop waarvan het zwaartepunt mag worden geacht te liggen in d-X3. De zaak ligt immers in evenwicht.
De vergelijking wordt hiermee 0,5 x X3 = 0,5 x (d-X3) + 2 x (d-X3). Oftewel X3 = d � X3 + 4 d � 4 X3, hetgeen oplevert 6 X3 = 5 d, dus X3 = 5/6 d. Tegel T3 steekt dus 1/6 tegel uit t.o.v. de onderliggende tegel T4.
De toren steekt nu uit 1/2 + 1/4 + 1/6 = 0,91 tegel.
Hoeveel kan T4 uitsteken t.o.v. T5 zodat T4 precies in evenwicht hangt (met T1, T2, en T3 nog aanwezig)?
0,5 x X4 = 0,5 x (d-X4) + 3 x (d-X4) hetgeen oplevert 8 X4 = 7 d, dus X4 = 7/8 d. Tegel T4 steekt dus 1/8 tegel uit t.o.v. de onderliggende tegel T5.
De toren steekt nu uit 1/2 + 1/4 + 1/6 + 1/8 = 1,04 tegel.
Hoeveel kan T5 uitsteken t.o.v. T6 zodat T5 precies in evenwicht hangt (met T1, T2, T3, en T4 nog aanwezig)?
0,5 x X5 = 0,5 x (d-X5) + 4 x (d-X5) hetgeen oplevert X5 = 9/10 d. Tegel T5 steekt dus 1/10 tegel uit t.o.v. de onderliggende tegel T6.
De toren steekt nu uit 1/2 + 1/4 + 1/6 + 1/8 + 1/10 = 1,14 tegel.
Deze reeks loopt natuurlijk gewoon door. Tegel 11 overschrijdt de 1,5 en tegel 31 overschrijdt de 2. Bij tegel 1000 zit je al op 3,7427. Bij tegel 5000 zit je op de 5,7432.
kun je niet zomaar de 1/2 laten staan. dat is nl de maximale stabiele uitwijking van de een-na onderste t.o.v. de onderste. Vervolgens doe je je berekening voor de steen erboven. Je gaat er dan aan voorbij dat het moment van de onderste NIET meer stabiel is.
Ik heb het nog niet uitgewerkt maar het lijkt me dat ie niet verder kan dan 1,5
[ Bericht 2% gewijzigd door -Pepe- op 12-12-2005 19:33:41 ]


Er zijn er een aantal die ik 100% zeker weet en een daarvan is dat die toren met tegels toch echt oneindig (of eigenlijk beter geformuleerd: willekeurig) ver kan.


En ik weet 100% zeker dat het niet oneindig ver opzij kan gaan.quote:Op maandag 12 december 2005 19:47 schreef thabit het volgende:
Er zijn er een aantal die ik 100% zeker weet en een daarvan is dat die toren met tegels toch echt oneindig (of eigenlijk beter geformuleerd: willekeurig) ver kan.
De toren (of een deel ervan) zal op den duur niet meer in evenwicht staan en omvallen.
Op zondag 8 maart 2009 21:38 schreef Danny het volgende:
fuck de policy. posten die hap!
fuck de policy. posten die hap!


Het antwoord is heel simpel te beredeneren, als volgt:quote:Op dinsdag 13 december 2005 00:45 schreef Jegorex het volgende:
[..]
En ik weet 100% zeker dat het niet oneindig ver opzij kan gaan.
De toren (of een deel ervan) zal op den duur niet meer in evenwicht staan en omvallen.
Je begin met een tegel.
Precies onder het zwaartepunt van die stapel van 1 leg je de rand van de volgende tegel.
Precies onder het zwaartepunt van die stapel van 2 leg je de rand van de volgende tegel.
Precies onder het zwaartepunt van die stapel van 3 leg je de rand van de volgende tegel.
Etc.
Nu in formules. Op elk moment tijdens het stapelen geldt:
De positie van het zwaartepunt is zw.
De stapel heeft tot dan toe N tegels.
De nieuw te plaatsen tegel ligt met de rand op positie zw.
De afstand tot het middelpunt van de nieuwe tegel is zw + 0.5.
Het zwaartepunt van de zo gelegde stapel is het gewogen gemiddelde van het zwaartepunt van de oude stapel + het zwaartepunt van de nieuwe tegel:
dus:
zw(nieuw) = (zw(oud) x N + zw + 0.5) / (N+1)
Ofwel:
zw(nieuw) = (zw(oud) x (N+1) + 0.5) / (N+1)
Ofwel
zw(nieuw) = zw(oud) + 0.5) / (N+1)
Ofwel
zw(nieuw) = zw(oud) + 1/ 2(N+1)
Begin met zw = 0, en N = 0, dan is de positie van het zwaartepunt na X tegels
(De som van 0 tot en met X van ) 1/2(N+1).
En dat is
1/2 + 1/4 + 1/6 + 1/8, etc.
deze reeks divergeert, dus wordt oneindig.
Het kan dus, een oneindige overhang, al is het totaal tegen je intuitie in!
Van: http://mathworld.wolfram.com/BookStackingProblem.html
* 11:15, restate my assumptions: 1. Mathematics is the language of nature. 2. Everything around us can be represented and understood through numbers. 3. If you graph these numbers, patterns emerge. Therefore: There are patterns everywhere in nature.*


De vraag is nu: gegeven een overhang van x, wat is het minimale aantal N(x) aan tegels dat ik nodig heb om x te bereiken. Komen we daar de harmonische reeks weer tegen, of is er een betere strategie? Gelieve geen onzin te antwoorden op deze vraag. M.a.w.: graag alleen reacties van thabit.
Wittgenstein


Als je enkel reactie wenst van thabit, kun je hem beter e-mailen dan je vraag op een publiek forum neerzetten.quote:Op dinsdag 13 december 2005 00:58 schreef Koekepan het volgende:
De vraag is nu: gegeven een overhang van x, wat is het minimale aantal N(x) aan tegels dat ik nodig heb om x te bereiken. Komen we daar de harmonische reeks weer tegen, of is er een betere strategie? Gelieve geen onzin te antwoorden op deze vraag. M.a.w.: graag alleen reacties van thabit.
* 11:15, restate my assumptions: 1. Mathematics is the language of nature. 2. Everything around us can be represented and understood through numbers. 3. If you graph these numbers, patterns emerge. Therefore: There are patterns everywhere in nature.*


Nou ja, zo bedoelde ik het natuurlijk niet. 't Was enkel een ontmoediging voor mensen die geen benul hebben maar wel graag interessant doen met ingewikkelde formules en zo.
Wittgenstein


De harmonische reeks levert uiteraard het beste resultaat.
Stel dat de tegels lengte 2 hebben, en hanteer als conventie dat de stapel nog altijd stabiel is als de rand van elke tegel recht onder het zwaartepunt van de deelstapel erboven zit. Mocht je deze eis willen laten vallen, dan kun je natuurlijk elke uitwijking krijgen die een epsilon minder is dan die van de harmonische reeks.
Stel dat het zwaartepunt van de bovenste steen op positie 0 zit, en dat we vanaf de bovenste steen in de positieve richting willen werken. Laat sn gedefinieerd zijn als de positie van het zwaartepunt van de n'de tegel.
Te bewijzen:
voor alle n.
We gebruiken nu volledige inductie naar n. Het geval n=1 is triviaal. Stel nu dat het geldt voor de bovenste n stenen. Waar zit het zwaartepunt van deze stenen?
Welnu, dat zit op positie
Omdat we de tegel eronder hooguit een afstand 1 verder kunnen krijgen dan dit zwaartepunt, geldt dat sn+1<= 1/1+...+1/n, hetgeen we moesten bewijzen.
De harmonische reeks geeft gelijkheid in de geLaTeXde afschatting en dit laat zien dat daar de stapel ook stabiel is.
[ Bericht 1% gewijzigd door thabit op 13-12-2005 12:17:09 ]
Stel dat de tegels lengte 2 hebben, en hanteer als conventie dat de stapel nog altijd stabiel is als de rand van elke tegel recht onder het zwaartepunt van de deelstapel erboven zit. Mocht je deze eis willen laten vallen, dan kun je natuurlijk elke uitwijking krijgen die een epsilon minder is dan die van de harmonische reeks.
Stel dat het zwaartepunt van de bovenste steen op positie 0 zit, en dat we vanaf de bovenste steen in de positieve richting willen werken. Laat sn gedefinieerd zijn als de positie van het zwaartepunt van de n'de tegel.
Te bewijzen:
voor alle n.
We gebruiken nu volledige inductie naar n. Het geval n=1 is triviaal. Stel nu dat het geldt voor de bovenste n stenen. Waar zit het zwaartepunt van deze stenen?
Welnu, dat zit op positie
Omdat we de tegel eronder hooguit een afstand 1 verder kunnen krijgen dan dit zwaartepunt, geldt dat sn+1<= 1/1+...+1/n, hetgeen we moesten bewijzen.
De harmonische reeks geeft gelijkheid in de geLaTeXde afschatting en dit laat zien dat daar de stapel ook stabiel is.
[ Bericht 1% gewijzigd door thabit op 13-12-2005 12:17:09 ]


Dat dacht ik ook ja:quote:Op dinsdag 13 december 2005 12:10 schreef thabit het volgende:
De harmonische reeks levert uiteraard het beste resultaat.
Stel dat de tegels lengte 2 hebben, en hanteer als conventie dat de stapel nog altijd stabiel is als de rand van elke tegel recht onder het zwaartepunt van de deelstapel erboven zit. Mocht je deze eis willen laten vallen, dan kun je natuurlijk elke uitwijking krijgen die een epsilon minder is dan die van de harmonische reeks.
Stel dat het zwaartepunt van de bovenste steen op positie 0 zit, en dat we vanaf de bovenste steen in de positieve richting willen werken. Laat sn gedefinieerd zijn als de positie van het zwaartepunt van de n'de tegel.
Te bewijzen: s1+...+sn<=1+1/2+...+1/(n-1).
We gebruiken nu volledige inductie naar n. Het geval n=1 is triviaal. Stel nu dat het geldt voor de bovenste n stenen. Waar zit het zwaartepunt van deze stenen?
Welnu, dat zit op positie
[afbeelding]
Omdat we de tegel eronder hooguit een afstand 1 verder kunnen krijgen dan dit zwaartepunt, geldt dat sn+1<= 1/1+...+1/n, hetgeen we moesten bewijzen.
De harmonische reeks geeft gelijkheid in de geLaTeXde afschatting en dit laat zien dat daar de stapel ook stabiel is.
Harmonische reeks: 1 + 1/2 + 1/3 + 1/4 + 1/5 .... 1/n
Een harmonisch getal Hn is deze reeks tot stap n herhaald.
Dus harmonisch getal 5 = 1 + 1/2 + 1/3 + 1/4 + 1/5.
De maximale overhang voor een stapel van n tegels blijkt te zijn:
Hn / 2.
Voor 5 tegels is de maximale overhang 1,142
Voor 30 tegels is dat 1.997
Voor 100 tegels is dat 2.59
Voor 1000 tegels 3,74.
Deze reeks is dus niet eindig.
Dat wil zeggen, het verschil tussen 1000 en 1001 tegels maakt natuurlijk erg weinig uit voor de overhang van de bovenste tegel, maar toch blijft met de hoogte de maximale overhang toenemen.
* 11:15, restate my assumptions: 1. Mathematics is the language of nature. 2. Everything around us can be represented and understood through numbers. 3. If you graph these numbers, patterns emerge. Therefore: There are patterns everywhere in nature.*


Deze manier van redeneren is natuurlijk onjuist. Er zijn zat reeksen die het beschreven eindige gedrag hebben voor de waarden 5, 30, 100 en 1000 en toch niet divergeren.quote:Op dinsdag 13 december 2005 12:16 schreef Quarks het volgende:
[..]
Voor 5 tegels is de maximale overhang 1,142
Voor 30 tegels is dat 1.997
Voor 100 tegels is dat 2.59
Voor 1000 tegels 3,74.
Deze reeks is dus niet eindig.


Maar het feit dat met de hoogte de maximale overhang blijft toenemen impliceert natuurlijk niet dat de reeks niet eindig isquote:Op dinsdag 13 december 2005 12:16 schreef Quarks het volgende:
[..]
Deze reeks is dus niet eindig.
Dat wil zeggen, het verschil tussen 1000 en 1001 tegels maakt natuurlijk erg weinig uit voor de overhang van de bovenste tegel, maar toch blijft met de hoogte de maximale overhang toenemen.


Had ik nou niet iets gezegd over onzinnige bijdragen? Dit is echt pijnlijk om te lezen voor iedereen met een béétje wiskundig besef.quote:Op dinsdag 13 december 2005 12:16 schreef Quarks het volgende:
[..]
Dat dacht ik ook ja:
Harmonische reeks: 1 + 1/2 + 1/3 + 1/4 + 1/5 .... 1/n
Een harmonisch getal Hn is deze reeks tot stap n herhaald.
Dus harmonisch getal 5 = 1 + 1/2 + 1/3 + 1/4 + 1/5.
De maximale overhang voor een stapel van n tegels blijkt te zijn:
Hn / 2.
Voor 5 tegels is de maximale overhang 1,142
Voor 30 tegels is dat 1.997
Voor 100 tegels is dat 2.59
Voor 1000 tegels 3,74.
Deze reeks is dus niet eindig.
Dat wil zeggen, het verschil tussen 1000 en 1001 tegels maakt natuurlijk erg weinig uit voor de overhang van de bovenste tegel, maar toch blijft met de hoogte de maximale overhang toenemen.
Wittgenstein


Je hebt gelijk, in het uitleggen ben ik zelf niet zo goed.quote:Op dinsdag 13 december 2005 12:20 schreef thabit het volgende:
[..]
Deze manier van redeneren is natuurlijk onjuist. Er zijn zat reeksen die het beschreven eindige gedrag hebben voor de waarden 5, 30, 100 en 1000 en toch niet divergeren.
Maar iedereen is het er nu wel over eens dat het antwoord oneindig moet zijn.
* 11:15, restate my assumptions: 1. Mathematics is the language of nature. 2. Everything around us can be represented and understood through numbers. 3. If you graph these numbers, patterns emerge. Therefore: There are patterns everywhere in nature.*


Mensen, mensen... vertel me liever hoe het met de eenden zitquote:Op dinsdag 13 december 2005 12:23 schreef Koekepan het volgende:
[..]
Had ik nou niet iets gezegd over onzinnige bijdragen? Dit is echt pijnlijk om te lezen voor iedereen met een béétje wiskundig besef.
En als je N(x) wil, dan heb je volgens mij de inverse van de digamma functie nodig...


Volgens mij staat dat hier al ergens. .quote:Op dinsdag 13 december 2005 12:32 schreef Doderok het volgende:
[..]
Mensen, mensen... vertel me liever hoe het met de eenden zit
Wittgenstein


Zij k een gegeven positief geheel getal. Voor elke n met 2k-1<n<=2k geldt trivialerwijs dat n<=2k en dus dat 1/n>=1/2k.
Er geldt dus
waaruit volgt dat
Het is duidelijk dat dit boven elke grens stijgt.
Er geldt dus
waaruit volgt dat
Het is duidelijk dat dit boven elke grens stijgt.


tv not rot brain..
Life is something to do when you can't get to sleep..
The snoozebar.. cause there's nothing like starting the day with a little procrastination
Life is something to do when you can't get to sleep..
The snoozebar.. cause there's nothing like starting the day with a little procrastination


Iedereen zegt 10->B (de trampoline, springveren moet je in je rugzak stoppen).
Wat echter als de trampoline superstrak gespannen is (zodat hij zo goed als niet veert)? Dan ben je toch echt beter af met verende schoenen.
10->B en 10->C is dus in ieder geval een fout antwoord bij een superstrakke trampoline.
Bij een meer verende trampoline ligt het misschien anders maar waar ligt dan het kantelpunt?
De vraag doet verder geen enkele uitspraak over de veerkracht van de trampoline of de schoenen dus blijft alleen antwoord A over.
[ Bericht 0% gewijzigd door yoppybt op 16-12-2005 14:08:51 ]
Wat echter als de trampoline superstrak gespannen is (zodat hij zo goed als niet veert)? Dan ben je toch echt beter af met verende schoenen.
10->B en 10->C is dus in ieder geval een fout antwoord bij een superstrakke trampoline.
Bij een meer verende trampoline ligt het misschien anders maar waar ligt dan het kantelpunt?
De vraag doet verder geen enkele uitspraak over de veerkracht van de trampoline of de schoenen dus blijft alleen antwoord A over.
[ Bericht 0% gewijzigd door yoppybt op 16-12-2005 14:08:51 ]


Nee hoor. In het ideale geval is er geen energieverlies en bereikt hij sowieso terug zijn oorspronkelijke hoogte. Het gaat om "hij zet zich zo hard mogelijk af". Hoe stijver de ondergrond (trampoline + bladveren), hoe meer effect dit afzetten zal hebben. Zonder bladveren dus.quote:Op vrijdag 16 december 2005 13:54 schreef yoppybt het volgende:
Iedereen zegt 10->B (de trampoline, springveren moet je in je rugzak stoppen).
Wat echter als de trampoline superstrak gespannen is (zodat hij zo goed als niet veert)? Dan ben je toch echt beter af met verende schoenen.
10->B en 10->C is dus in ieder geval een fout antwoord bij een superstrakke trampoline.
Bij een meer verende trampoline ligt het misschien anders maar waar ligt dan het kantelpunt?
De vraag doet verder geen enkele uitspraak over de veerkracht van de trampoline of de schoenen dus blijft alleen antwoord A over.
|
|