[Bèta wiskunde] Huiswerk- en vragentopic.

Index

» school, studie en onderwijs

actieve topics nieuwe topics
abonnement Unibet Coolblue
pi_151714150
quote:
0s.gif Op woensdag 15 april 2015 16:43 schreef jatochneetoch het volgende:

[..]

Oke bedankt ik denk dat ik het snap. :)

Nu heb nog nog een andere waar ik net tegen aan liep. Misschien dat je me daar ook mee kan helpen?
\\\ddot{y}+x=0\\\ddot{x}+y=0
Write this system as four coupled first order equations.

Weet jij wat hoe je dit doet?
Definieer u en v als

x' = u
y' = v

dan worden je vergelijkingen first-order

u' = - y
v' = - x

vier in totaal
pi_151714675
quote:
0s.gif Op woensdag 15 april 2015 17:21 schreef Anoonumos het volgende:

[..]

Definieer u en v als

x' = u
y' = v

dan worden je vergelijkingen first-order

u' = - y
v' = - x

vier in totaal
Oke bedankt.

vervolgens vragen ze de eigenwaardes en vectoren te berekenen.
Kan dat met de volgende vergelijking?
\begin{Bmatrix}\ddot{x}\\ \ddot{y}\end{Bmatrix}=\begin{bmatrix}0 &-1 \\ -1 & 0\end{bmatrix}\begin{Bmatrix}x\\y \end{Bmatrix}

Bij alle voorbeelden hebben ze een eerste orde vergelijking, dus weet niet of het zo mag.
Of moet ik dan die u en v er in verwerken?
pi_151716055
quote:
0s.gif Op woensdag 15 april 2015 17:40 schreef jatochneetoch het volgende:

[..]

Oke bedankt.

vervolgens vragen ze de eigenwaardes en vectoren te berekenen.
Kan dat met de volgende vergelijking?
\begin{Bmatrix}\ddot{x}\\ \ddot{y}\end{Bmatrix}=\begin{bmatrix}0 &-1 \\ -1 & 0\end{bmatrix}\begin{Bmatrix}x\\y \end{Bmatrix}

Bij alle voorbeelden hebben ze een eerste orde vergelijking, dus weet niet of het zo mag.
Of moet ik dan die u en v er in verwerken?
Met x,y,u en v (dus 4x4 matrix) ja.
Jouw systeem werkt niet.
pi_151726319
quote:
0s.gif Op woensdag 15 april 2015 11:24 schreef jatochneetoch het volgende:
Hallo,

Ik heb morgen een tentamen over differentiaal vergelijkingen.
Nou ben ik bezig met oefententamens en nou komt er bij 2 oefententamens een som voor waar ik geen idee heb hoe ik hem moet maken. En natuurlijk zijn er geen uitwerkingen beschikbaar en kan ik ook geen zelfde soort opgave in het boek vinden :'(



Kan iemand mij uitleggen wat hier de bedoeling is?

Alvast bedankt :)
Dit is een zogenaamde exacte DV. Beide kanten 'vermenigvuldigen' met dx en je hebt
(x^3 + \dfrac{y}{x})\mathrm{d}x + (y^2 + \ln (x))\mathrm{d}y = g(x,y)\mathrm{d}x + h(x,y)\mathrm{d}y= 0

We gaan nu op zoek naar een Potential function , F:\mathbb{R}^2 \to \mathbb{R} , die voldoet aan F_x = g en F_y = h
F(x,y) = \int g(x,y) \mathrm{d}x + C(y) = \dfrac{1}{4}x^4 + y \ln(x) + C(y)
Differentiëren naar y resulteert in
F_y(x,y) = \ln (x) + C'(y) = h = y^2 + \ln(x)\Longrightarrow C'(y) = y^2 \Longrightarrow C(y) = \dfrac{1}{3}y^3
Dus we hebben nu F(x,y) = \dfrac{1}{4}x^4 + y \ln(x) +\dfrac{1}{3}y^3
En daarmee de impliciete oplossing F(x,y) = K . Waar {K} wordt bepaald door de initiële waarde.
pi_151872574
Hallo all,

Wellicht een simpele vraag maar ik kom er met wat googlen niet helemaal uit.
Stel ik heb een aantal klassen die zijn verdeeld naar leeftijd:

< 15
15 - < 30
30 - < 55
> 55

nu wordt er gevraagd om de gemiddelde leeftijd. Nu weet ik dat je dat alleen maar kan schatten door klassenmidden te vermenigvuldigen met de frequentie en dan delen door totaal.

Echter wat doe ik met die laatste klasse, moet ik die ergens capppen?
Wat is hier gebruikelijk om te doen?
pi_151880073
quote:
1s.gif Op maandag 20 april 2015 21:08 schreef FortunaHome het volgende:
Hallo all,

Wellicht een simpele vraag maar ik kom er met wat googlen niet helemaal uit.
Stel ik heb een aantal klassen die zijn verdeeld naar leeftijd:

< 15
15 - < 30
30 - < 55
> 55

nu wordt er gevraagd om de gemiddelde leeftijd. Nu weet ik dat je dat alleen maar kan schatten door klassenmidden te vermenigvuldigen met de frequentie en dan delen door totaal.

Echter wat doe ik met die laatste klasse, moet ik die ergens capppen?
Wat is hier gebruikelijk om te doen?
Als x>55 de levensverwachting is, dan zou je 55 + (x-55)/2 kunnen nemen als gemiddelde in die laatste categorie. Maar het is natuurlijk natte-vingerwerk.
  zondag 3 mei 2015 @ 23:43:31 #182
302030 Amoeba
Floydiaan.
pi_152251393
Zij f(z) een holomorfe functie op de open set V.

Bewijs dat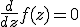 \frac{d}{dz}f(z) = 0

Tevens is f van de vorm f = u + iv met i,v reële functies.
Daarnaast is de hint schrijf x als 1/2(z+z_ ) en y als -i/2(z-z_) met z_ de complex geconjugeerde van z.

Iemand enig idee? Ik kom er niet echt uit
Fervent tegenstander van het korps lasergamers.
pi_152251766
quote:
2s.gif Op zondag 3 mei 2015 23:43 schreef Amoeba het volgende:
Zij f(z) een holomorfe functie op de open set V.

Bewijs dat \frac{d}{dz}f(z) = 0

Tevens is f van de vorm f = u + iv met i,v reële functies.
Daarnaast is de hint schrijf x als 1/2(z+z_ ) en y als -i/2(z-z_) met z_ de complex geconjugeerde van z.

Iemand enig idee? Ik kom er niet echt uit
Ik neem aan dat je \frac{d}{d\overline{z}}f(z)=0 bedoelt.
  maandag 4 mei 2015 @ 00:40:23 #184
302030 Amoeba
Floydiaan.
pi_152252489
quote:
0s.gif Op zondag 3 mei 2015 23:59 schreef thabit het volgende:

[..]

Ik neem aan dat je \frac{d}{d\overline{z}}f(z)=0 bedoelt.
Ah, ja, sorry.
Fervent tegenstander van het korps lasergamers.
pi_152254144
Of beter nog: \frac{\partial}{\partial\overline{z}}f(z)=0.

Hint: wat zijn \frac{\partial}{\partial{z}} en \frac{\partial}{\partial\overline{z}} in termen van \frac{\partial}{\partial x} en \frac{\partial}{\partial y}?
pi_152272918
Ik volg een vak waarin C0-semigroups behandeld worden. Ik moet laten zien dat als Y een T(t)-invariante, 1-dimensionale lineaire deelruimte van X is, dat Y dan wordt opgespannen door een eigenvector van A, de infinitesimal generator van T.

Als iemand een idee heeft waar ik kan beginnen, hoor ik het graag. Ik snap niet waarom de T(t)-invariante ruimte geen 'cirkel' kan zijn, als het ware. Als hint hebt ik gekregen:

If a continuous scalar function f satisfies f(t + s) = f(t)f(s) for t, s in [0, infinity), then f(t) = ect for some c.

Maar je hebt geen functies naar R. J hebt wel die C0-semigroup die voldoet aan T(t + s) = T(t)T(s), maar ik zie niet wat dit te maken heeft met een functie naar R. Ideeen zijn erg welkom :)
pi_152302061
Een vraag die eenvoudig zou moeten zijn maar waar ik een beginnetje mis;

Bewijs voor f,g : Rn → R continu dat de verzameling { x in Rn | f(x) < g(x) } open is.

Ik vermoed dat ik het volledig origineel f-1(R) moet gebruiken, en de stelling dat voor een continue functie h: V → W geldt dat van iedere open deelverzameling O in W het volledig origineel h-1(O) open is in V. Maar waar begin ik?

[ Bericht 3% gewijzigd door Diacetylmorfine op 05-05-2015 17:06:38 ]
Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caparet
  dinsdag 5 mei 2015 @ 17:18:04 #188
302030 Amoeba
Floydiaan.
pi_152302653
quote:
0s.gif Op maandag 4 mei 2015 07:41 schreef thabit het volgende:
Of beter nog: \frac{\partial}{\partial\overline{z}}f(z)=0.

Hint: wat zijn \frac{\partial}{\partial{z}} en \frac{\partial}{\partial\overline{z}} in termen van \frac{\partial}{\partial x} en \frac{\partial}{\partial y}?
d/dz = 1/2(d/dx - i*d/dy) en d/dz_ = 1/2(d/dx + i*d/dy)

f = u+i*v substitueren, gebruik maken van de Cauchy-Riemann vergelijkingen voor partiële afgeleiden en het gevraagde volgt. Dank ^O^
Fervent tegenstander van het korps lasergamers.
pi_152306819
quote:
2s.gif Op zondag 3 mei 2015 23:43 schreef Amoeba het volgende:
Zij f een holomorfe functie op de open set V.

Bewijs dat

\frac{\partial}{\partial \overline{z}}f(z,\,\overline{z}) \,=\,0

Tevens is f van de vorm f(z, z̅) = u(x, y) + i·v(x, y) waarbij u en v reële functies zijn van de reële variabelen x en y met z = x + iy.

Daarnaast is de hint schrijf x als ½(z + z̅) en y als −½i(z − z̅) waarbij z̅ = x − iy de complex geconjugeerde is van z.

Iemand enig idee? Ik kom er niet echt uit.
We vatten f op als een functie van z en z̅ en ook x = ½(z + z̅) en y = −½i(z − z̅) als functies van z en z̅ zodat we kunnen schrijven

(1)\quad f(z,\,\overline{z})\,=\,u(x(z,\,\overline{z}),\,y(z,\,\overline{z}))\,+\,i \cdot v(x(z,\,\overline{z}),\,y(z,\,\overline{z}))

Nu zijn z en z̅ niet onafhankelijk van elkaar, maar we kunnen formeel doen alsof dat wel het geval is en differentiëren van (1) naar z̅ geeft dan met behulp van de kettingregel

(2)\quad \frac{\partial}{\partial\overline{z}}f(z,\,\overline{z})\,=\,\left(\frac{\partial u}{\partial x}\,\frac{\partial x}{\partial\overline{z}}\,+\,\frac{\partial u}{\partial y}\,\frac{\partial y}{\partial\overline{z}}\right)\,+\,i\cdot\left(\frac{\partial v}{\partial x}\,\frac{\partial x}{\partial\overline{z}}\,+\,\frac{\partial v}{\partial y}\,\frac{\partial y}{\partial\overline{z}}\right)

Maar nu is x = ½(z + z̅) en y = −½i(z − z̅) zodat ook

(3)\quad \frac{\partial x}{\partial\overline{z}}\,=\,\frac{1}{2}

en

(4)\quad \frac{\partial y}{\partial\overline{z}}\,=\,\frac{1}{2}i

Substitutie van (3) en (4) in (2) en uitwerken en hergroeperen van de reële en imaginaire termen geeft nu

(5)\quad \frac{\partial}{\partial\overline{z}}f(z,\,\overline{z})\,=\,\frac{1}{2}\left(\frac{\partial u}{\partial x}\,-\,\frac{\partial v}{\partial y}\right)\,+\,i\cdot\frac{1}{2}\left(\frac{\partial u}{\partial y}\,+\,\frac{\partial v}{\partial x}\right)

zodat de voorwaarde

(6)\quad \frac{\partial}{\partial \overline{z}}f(z,\,\overline{z}) \,=\,0

equivalent is met

(7)\quad \frac{\partial u}{\partial x}\,=\,\frac{\partial v}{\partial y}\quad\wedge\quad\frac{\partial u}{\partial y}\,=\,-\,\frac{\partial v}{\partial x}

en dit zijn de vergelijkingen van Cauchy-Riemann voor een holomorfe functie f(x + iy) = u(x, y) + i·v(x, y). Aangezien is gegeven dat f holomorf is voldoet deze functie aan (7) en daarmee ook aan (6), QED.

We zien dus dat (6) een equivalente uitdrukking is voor de vergelijkingen van Cauchy-Riemann. Eenvoudig gezegd komt het erop neer dat een holomorfe functie van een complexe variabele z een functie is die onafhankelijk is van de geconjugeerde z̅.

We kunnen ditzelfde resultaat ook op een iets andere manier vinden, namelijk door omgekeerd z = x + iy en z̅ = x − iy op te vatten als functies van x en y. Differentiëren van f(z(x, y), z̅(x, y)) naar x en naar y geeft met behulp van de kettingregel

(8)\quad \frac{\partial}{\partial x}f(z(x,\,y),\,\overline{z}(x,\,y))\,=\,\frac{\partial z}{\partial x}\cdot\frac{\partial}{\partial z}f(z(x,\,y),\,\overline{z}(x,\,y))\,+\,\frac{\partial\overline{z}}{\partial x}\cdot\frac{\partial}{\partial\overline{z}}f(z(x,\,y),\,\overline{z}(x,\,y))

resp.

(9)\quad \frac{\partial}{\partial y}f(z(x,\,y),\,\overline{z}(x,\,y))\,=\,\frac{\partial z}{\partial y}\cdot\frac{\partial}{\partial z}f(z(x,\,y),\,\overline{z}(x,\,y))\,+\,\frac{\partial\overline{z}}{\partial y}\cdot\frac{\partial}{\partial\overline{z}}f(z(x,\,y),\,\overline{z}(x,\,y))

Formeel kunnen we (8) en (9) eenvoudiger noteren als betrekkingen tussen differentiaaloperatoren, namelijk als

(10)\quad \frac{\partial}{\partial x}\,=\,\frac{\partial z}{\partial x}\,\frac{\partial}{\partial z}\,+\,\frac{\partial\overline{z}}{\partial x}\,\frac{\partial}{\partial\overline{z}}

resp.

(11)\quad \frac{\partial}{\partial y}\,=\,\frac{\partial z}{\partial y}\,\frac{\partial}{\partial z}\,+\,\frac{\partial\overline{z}}{\partial y}\,\frac{\partial}{\partial\overline{z}}

Maar nu volgt uit z = x + iy en z̅ = x − iy dat

(12)\quad \frac{\partial z}{\partial x}\,=\,1,\quad\frac{\partial z}{\partial y}\,=\,i,\quad\frac{\partial\overline{z}}{\partial x}\,=\,1,\quad\frac{\partial\overline{z}}{\partial y}\,=\,-i

zodat we voor (10) en (11) kunnen schrijven

(13)\quad \frac{\partial}{\partial x}\,=\,\frac{\partial}{\partial z}\,+\,\frac{\partial}{\partial\overline{z}}

resp.

(14)\quad \frac{\partial}{\partial y}\,=\,i\cdot\left(\frac{\partial}{\partial z}\,-\,\frac{\partial}{\partial\overline{z}}\right)

Lossen we ∂/∂z en ∂/∂z̅ op uit (13) en (14) dan krijgen we

(15)\quad \frac{\partial}{\partial z}\,=\,\frac{1}{2}\left(\frac{\partial}{\partial x}\,-\,i\frac{\partial}{\partial y} \right)

en

(16)\quad \frac{\partial}{\partial\overline{z}}\,=\,\frac{1}{2}\left(\frac{\partial}{\partial x}\,+\,i\frac{\partial}{\partial y}\right)

De betrekkingen (15) en (16) heten de differentiaaloperatoren van Wirtinger. Met behulp van (16) krijgen we direct

(17)\quad \frac{\partial}{\partial\overline{z}}f(z,\,\overline{z})\,=\,\frac{1}{2}\left(\frac{\partial}{\partial x}\,+\,i\frac{\partial}{\partial y}\right)\left(u\,+\,iv\right)

en uitwerken hiervan levert inderdaad (5).

[ Bericht 2% gewijzigd door Riparius op 05-05-2015 21:45:02 ]
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
pi_152307028
quote:
11s.gif Op dinsdag 5 mei 2015 16:59 schreef Diacetylmorfine het volgende:
Een vraag die eenvoudig zou moeten zijn maar waar ik een beginnetje mis;

Bewijs voor f,g : Rn → R continu dat de verzameling { x in Rn | f(x) < g(x) } open is.

Ik vermoed dat ik het volledig origineel f-1(R) moet gebruiken, en de stelling dat voor een continue functie h: V → W geldt dat van iedere open deelverzameling O in W het volledig origineel h-1(O) open is in V. Maar waar begin ik?
Gebruik dat (f,g) : Rn→R2 : x ↦ (f(x), g(x)) continu is. Je kan ook gebruiken dat f-g continu is. Ienemienemutte.
pi_152307140
quote:
0s.gif Op maandag 4 mei 2015 19:49 schreef defineaz het volgende:
Ik volg een vak waarin C0-semigroups behandeld worden. Ik moet laten zien dat als Y een T(t)-invariante, 1-dimensionale lineaire deelruimte van X is, dat Y dan wordt opgespannen door een eigenvector van A, de infinitesimal generator van T.

Als iemand een idee heeft waar ik kan beginnen, hoor ik het graag. Ik snap niet waarom de T(t)-invariante ruimte geen 'cirkel' kan zijn, als het ware.
Het is gegeven dat Y lineair is.
  dinsdag 5 mei 2015 @ 19:56:00 #192
302030 Amoeba
Floydiaan.
pi_152307446
quote:
0s.gif Op dinsdag 5 mei 2015 19:39 schreef Riparius het volgende:

[..]

We vatten f op als een functie van z en z̅ en ook x = ½(z + z̅) en y = −½i(z − z̅) als functies van z en z̅ zodat we kunnen schrijven

(1)\quad f(z,\,\overline{z})\,=\,u(x(z,\,\overline{z}),\,y(z,\,\overline{z}))\,+\,i \cdot v(x(z,\,\overline{z}),\,y(z,\,\overline{z}))

Nu zijn z en z̅ niet onafhankelijk van elkaar, maar we kunnen formeel doen alsof dat wel het geval is en differentiëren van (1) naar z̅ geeft dan met behulp van de kettingregel

(2)\quad \frac{\partial}{\partial\overline{z}}f(z,\,\overline{z})\,=\,\left(\frac{\partial u}{\partial x}\,\frac{\partial x}{\partial\overline{z}}\,+\,\frac{\partial u}{\partial y}\,\frac{\partial y}{\partial\overline{z}}\right)\,+\,i\cdot\left(\frac{\partial v}{\partial x}\,\frac{\partial x}{\partial\overline{z}}\,+\,\frac{\partial v}{\partial y}\,\frac{\partial y}{\partial\overline{z}}\right)

Maar nu is x = ½(z + z̅) en y = −½i(z − z̅) zodat ook

(3)\quad \frac{\partial x}{\partial\overline{z}}\,=\,\frac{1}{2}

en

(4)\quad \frac{\partial y}{\partial\overline{z}}\,=\,\frac{1}{2}i

Substitutie van (3) en (4) in (2) en uitwerken en hergroeperen van de reële en imaginaire termen geeft nu

(5)\quad \frac{\partial}{\partial\overline{z}}f(z,\,\overline{z})\,=\,\frac{1}{2}\left(\frac{\partial u}{\partial x}\,-\,\frac{\partial v}{\partial y}\right)\,+\,i\cdot\frac{1}{2}\left(\frac{\partial u}{\partial y}\,+\,\frac{\partial v}{\partial x}\right)

zodat de voorwaarde

(6)\quad \frac{\partial}{\partial \overline{z}}f(z,\,\overline{z}) \,=\,0

equivalent is met

(7)\quad \frac{\partial u}{\partial x}\,=\,\frac{\partial v}{\partial y}\quad\wedge\quad\frac{\partial u}{\partial y}\,=\,-\,\frac{\partial v}{\partial x}

en dit zijn de vergelijkingen van Cauchy-Riemann voor een holomorfe functie f(x + iy) = u(x, y) + i·v(x, y). Aangezien is gegeven dat f holomorf is voldoet deze aan (7) en daarmee ook aan (6), QED.

We zien dus dat (6) een equivalente uitdrukking is voor de vergelijkingen van Cauchy-Riemann. Eenvoudig gezegd komt het erop neer dat een holomorfe functie van een complexe variabele z een functie is die onafhankelijk is van de geconjugeerde z̅.

We kunnen ditzelfde resultaat ook op een iets andere manier vinden, namelijk door omgekeerd z = x + iy en z̅ = x − iy op te vatten als functies van x en y. Differentiëren van f(z(x, y), z̅(x, y)) naar x en naar y geeft met behulp van de kettingregel

(8)\quad \frac{\partial}{\partial x}f(z(x,\,y),\,\overline{z}(x,\,y))\,=\,\frac{\partial}{\partial z}f(z(x,\,y),\,\overline{z}(x,\,y))\cdot\frac{\partial z}{\partial x}\,+\,\frac{\partial}{\partial\overline{z}}f(z(x,\,y),\,\overline{z}(x,\,y))\cdot\frac{\partial\overline{z}}{\partial x}

resp.

(9)\quad \frac{\partial}{\partial y}f(z(x,\,y),\,\overline{z}(x,\,y))\,=\,\frac{\partial}{\partial z}f(z(x,\,y),\,\overline{z}(x,\,y))\cdot\frac{\partial z}{\partial y}\,+\,\frac{\partial}{\partial\overline{z}}f(z(x,\,y),\,\overline{z}(x,\,y))\cdot\frac{\partial\overline{z}}{\partial y}

Formeel kunnen we (8) en (9) eenvoudiger noteren als betrekkingen tussen differentiaaloperatoren, namelijk als

(10)\quad \frac{\partial}{\partial x}\,=\,\frac{\partial}{\partial z}\,\frac{\partial z}{\partial x}\,+\,\frac{\partial}{\partial\overline{z}}\,\frac{\partial\overline{z}}{\partial x}

resp.

(11)\quad \frac{\partial}{\partial y}\,=\,\frac{\partial}{\partial z}\,\frac{\partial z}{\partial y}\,+\,\frac{\partial}{\partial\overline{z}}\,\frac{\partial\overline{z}}{\partial y}

Maar nu volgt uit z = x + iy en z̅ = x − iy dat

(12)\quad \frac{\partial z}{\partial x}\,=\,1,\quad\frac{\partial z}{\partial y}\,=\,i,\quad\frac{\partial\overline{z}}{\partial x}\,=\,1,\quad\frac{\partial\overline{z}}{\partial y}\,=\,-i

zodat we voor (10) en (11) kunnen schrijven

(13)\quad \frac{\partial}{\partial x}\,=\,\frac{\partial}{\partial z}\,+\,\frac{\partial}{\partial\overline{z}}

resp.

(14)\quad \frac{\partial}{\partial y}\,=\,i\cdot\left(\frac{\partial}{\partial z}\,-\,\frac{\partial}{\partial\overline{z}}\right)

Lossen we ∂/∂z en ∂/∂z̅ op uit (13) en (14) dan krijgen we

(15)\quad \frac{\partial}{\partial z}\,=\,\frac{1}{2}\left(\frac{\partial}{\partial x}\,-\,i\frac{\partial}{\partial y} \right)

en

(16)\quad \frac{\partial}{\partial\overline{z}}\,=\,\frac{1}{2}\left(\frac{\partial}{\partial x}\,+\,i\frac{\partial}{\partial y}\right)

De betrekkingen (15) en (16) heten de differentiaaloperatoren van Wirtinger. Met behulp van (16) krijgen we direct

(17)\quad \frac{\partial}{\partial\overline{z}}f(z,\,\overline{z})\,=\,\frac{1}{2}\left(\frac{\partial}{\partial x}\,+\,i\frac{\partial}{\partial y}\right)\left(u\,+\,iv\right)

en uitwerken hiervan levert inderdaad (5).
Hulde! ^O^

Ik heb nog een andere vraag, het gaat over complex integreren.

Zij f(z) = \frac{1}{z^2+1}

Toon aan: lim_{R \rightarrow \infty} \int_K f(z) dz = 0

Waarbij K de halve cirkel met straal R is z.d.d. Im(z) ≥ 0.

Ik vond het een wijs idee om z(t) = R(cos(t)+i*sin(t)) als parametrisering voor K te handhaven.

Dan hebben we dat:

lim_{R \rightarrow \infty} \int_K f(z) dz =lim_{R \rightarrow \infty} \int_0^\pi \frac{z'(t)}{(z(t))^2 + 1} dt = lim_{R \rightarrow \infty} [arctan(z(t))]_0^\pi . Merk op dat moet gelden R =/= 1, maar dat is gezien de limiet geen probleem.

Het uitrekenen geeft

= lim_{R \rightarrow \infty} arctan(R(cos(\pi) + i\cdot sin(\pi))) - arctan(R(cos(0) + i\cdot sin(0)))
= lim_{R \rightarrow \infty} arctan(-R) - arctan(R)
= -\pi/2 - \pi/2 = -\pi

Nu heb ik een uitwerking gezien die gebruik maakt van het afschatten van de absolute waarde van de integraal met behulp van het ML-lemma, maar ik zie echt niet waar dit mis gaat. Wellicht kan iemand de vinger op de zere plek leggen?

Dus voor de duidelijkheid, ik ken het bewijs met het afschatten met het ML-lemma. Maar ik vraag me af waarom dit niet werkt. :')

[ Bericht 0% gewijzigd door Amoeba op 05-05-2015 20:08:12 ]
Fervent tegenstander van het korps lasergamers.
pi_152308327
quote:
0s.gif Op dinsdag 5 mei 2015 19:45 schreef thabit het volgende:

[..]

Gebruik dat (f,g) : Rn→R2 : x ↦ (f(x), g(x)) continu is. Je kan ook gebruiken dat f-g continu is. Ienemienemutte.
Ja, mijn eerste idee was om te gebruiken dat omdat f(x) < g(x), || f(x) - g(x) || > 0. Maar waar werk ik dan heen? Ik heb niet echt een idee van hoe ik bewijs dat de afbeelding van f(x), gegeven f(x) < g(x), open is.

Edit: wacht, is het dan niet afdoende te bewijzen dat er een omgeving bestaat rondom het punt f(x) waar het punt g(x) geen deel van uit maakt?

[ Bericht 3% gewijzigd door Diacetylmorfine op 05-05-2015 20:26:38 ]
Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caparet
pi_152308404
quote:
14s.gif Op dinsdag 5 mei 2015 19:56 schreef Amoeba het volgende:

Dus voor de duidelijkheid, ik ken het bewijs met het afschatten met het ML-lemma. Maar ik vraag me af waarom dit niet werkt. :')
Dat werkt zo niet omdat arctan z = ½i(log(1 − iz) − log(1 + iz)) niet eenduidig is voor een complexe z.
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
  dinsdag 5 mei 2015 @ 20:18:57 #195
302030 Amoeba
Floydiaan.
pi_152308436
quote:
0s.gif Op dinsdag 5 mei 2015 20:18 schreef Riparius het volgende:

[..]

Dat werkt zo niet omdat arctan z = ½i(log(1 − iz) − log(1 + iz)) niet eenduidig is voor een complexe z.
Ah dat wist ik dan weer niet. M'n hoofd over zitten breken vanochtend. :')
Fervent tegenstander van het korps lasergamers.
pi_152309247
quote:
5s.gif Op dinsdag 5 mei 2015 20:16 schreef Diacetylmorfine het volgende:

[..]

Ja, mijn eerste idee was om te gebruiken dat omdat f(x) < g(x), || f(x) - g(x) || > 0. Maar waar werk ik dan heen? Ik heb niet echt een idee van hoe ik bewijs dat de afbeelding van f(x), gegeven f(x) < g(x), open is.

Edit: wacht, is het dan niet afdoende te bewijzen dat er een omgeving bestaat rondom het punt f(x) waar het punt g(x) geen deel van uit maakt?
Als h(x) = f(x) - g(x), dan ben je dus op zoek naar het inverse beeld van ]-∞, 0[ onder h.
pi_152310654
quote:
14s.gif Op dinsdag 5 mei 2015 19:56 schreef Amoeba het volgende:

[..]

Hulde! ^O^

Ik heb nog een andere vraag, het gaat over complex integreren.

Zij f(z) = \frac{1}{z^2+1}

Toon aan: lim_{R \rightarrow \infty} \int_K f(z) dz = 0

Waarbij K de halve cirkel met straal R is z.d.d. Im(z) ≥ 0.

Ik vond het een wijs idee om z(t) = R(cos(t)+i*sin(t)) als parametrisering voor K te handhaven.

Dan hebben we dat:

lim_{R \rightarrow \infty} \int_K f(z) dz =lim_{R \rightarrow \infty} \int_0^\pi \frac{z'(t)}{(z(t))^2 + 1} dt = lim_{R \rightarrow \infty} [arctan(z(t))]_0^\pi . Merk op dat moet gelden R =/= 1, maar dat is gezien de limiet geen probleem.

Het uitrekenen geeft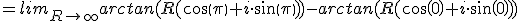

= lim_{R \rightarrow \infty} arctan(R(cos(\pi) + i\cdot sin(\pi))) - arctan(R(cos(0) + i\cdot sin(0)))
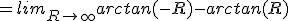
= lim_{R \rightarrow \infty} arctan(-R) - arctan(R)
= -\pi/2 - \pi/2 = -\pi

Nu heb ik een uitwerking gezien die gebruik maakt van het afschatten van de absolute waarde van de integraal met behulp van het ML-lemma, maar ik zie echt niet waar dit mis gaat. Wellicht kan iemand de vinger op de zere plek leggen?

Dus voor de duidelijkheid, ik ken het bewijs met het afschatten met het ML-lemma. Maar ik vraag me af waarom dit niet werkt. :')
Waarom niet eerst breuksplitsen?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
  dinsdag 5 mei 2015 @ 21:08:18 #198
302030 Amoeba
Floydiaan.
pi_152310859
quote:
0s.gif Op dinsdag 5 mei 2015 21:04 schreef Mathemaat het volgende:

[..]

Waarom niet eerst breuksplitsen?
Komt het dan wel uit?
Fervent tegenstander van het korps lasergamers.
pi_152311096
quote:
0s.gif Op dinsdag 5 mei 2015 21:08 schreef Amoeba het volgende:

[..]

Komt het dan wel uit?
O wacht. Ik heb je vraag verkeerd begrepen. Je integreert alleen over de boog, dus dan zou ik het afschatten.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
pi_152311642


[ Bericht 51% gewijzigd door Mathemaat op 05-05-2015 21:24:54 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
actieve topics nieuwe topics
abonnement Unibet Coolblue
[Bèta wiskunde] Huiswerk- en vragentopic.
Index

» school, studie en onderwijs

Forum Opties
Forumhop:
Hop naar:
(afkorting, bv 'KLB')