SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Ben er uiteindelijk achter second + 2 7 en dan aanvinken en del knopje.quote:Op maandag 27 oktober 2014 17:59 schreef t4rt4rus het volgende:
[..]
[2nd][+][7]
Dan ga je naar rechts naar de tab ALL en wat je dan moest doen weet ik niet meer.
Maar waarschijnlijk op enter drukken.
Heb je ook nog een wiskundige vraag?
Ja ik heb nog wel een vraag,
Ik moet bewijzen of deze functie convergent of divergent is
integraal (5x^-1 . E^2-2x)
Echter kan ik nu niet integration by parts gebruiken omdat je oneindig door gaat met deze functie.
Heeft iemand een tip voor dit probleem?


Majorant Theorem. Staat ergens in je lecture notes en anders achteraan in het gele boekje.quote:Op maandag 27 oktober 2014 18:39 schreef ibri het volgende:
[..]
Ben er uiteindelijk achter second + 2 7 en dan aanvinken en del knopje.
Ja ik heb nog wel een vraag,
Ik moet bewijzen of deze functie convergent of divergent is
integraal (5x^-1 . E^2-2x)
Echter kan ik nu niet integration by parts gebruiken omdat je oneindig door gaat met deze functie.
Heeft iemand een tip voor dit probleem?


Danku novermars,quote:Op maandag 27 oktober 2014 18:44 schreef Novermars het volgende:
[..]
Majorant Theorem. Staat ergens in je lecture notes en anders achteraan in het gele boekje.
Normaal bewijs ik het door dat er een oppervlakte bestaat, bijvoorbeeld lim e^-x wordt dan 0 en houd je vaak een bestaande oppervlakte over.
Ik zou er even naar kijken
Bij de sin en cos doen ze het tussen absolut value haken wat ik wel snap omdat het maximaal 1 is bij een sin of cos binnen absolut value haken.
5^-x wordt ook bijna 0 dus zal hij wel convergent zijn?


Wat zijn eigenlijk de integratiegrenzen? Vanaf x=1 neem ik aan...?quote:Op maandag 27 oktober 2014 18:55 schreef ibri het volgende:
[..]
Danku novermars,
Normaal bewijs ik het door dat er een oppervlakte bestaat, bijvoorbeeld lim e^-x wordt dan 0 en houd je vaak een bestaande oppervlakte over.
Ik zou er even naar kijken
Bij de sin en cos doen ze het tussen absolut value haken wat ik wel snap omdat het maximaal 1 is bij een sin of cos binnen absolut value haken.
5^-x wordt ook bijna 0 dus zal hij wel convergent zijn?


de grenzen zijn van 7 tot infinityquote:Op maandag 27 oktober 2014 19:01 schreef Novermars het volgende:
[..]
Wat zijn eigenlijk de integratiegrenzen? Vanaf x=1 neem ik aan...?


Ik was rustig aan het avondeten, als het iets langer duurt hoef je niet meteen een pm te sturen hoor.quote:
Maar wat je stuurde klopt.


Had een vraagje over wiskundige economie, bereken the elasticity of substitution between y and x for F(x, y) = 10x2 + 15y2 .
Nu heb ik eerst de marginal rate of substitution berekend = Ryx = 2x/3y .
Maar zie niet in hoe ik dit kan gebruiken om the elasticity of substitution te berekenen.
Nu heb ik eerst de marginal rate of substitution berekend = Ryx = 2x/3y .
Maar zie niet in hoe ik dit kan gebruiken om the elasticity of substitution te berekenen.


Kom eens met de definities van MRS en EOS.quote:Op maandag 27 oktober 2014 21:44 schreef uvastudentje het volgende:
Had een vraagje over wiskundige economie, bereken the elasticity of substitution between y and x for F(x, y) = 10x2 + 15y2 .
Nu heb ik eerst de marginal rate of substitution berekend = Ryx = 2x/3y .
Maar zie niet in hoe ik dit kan gebruiken om the elasticity of substitution te berekenen.
Ik kan er zo niet een goede wiskundige definitie van vinden.
Oh hier staat iets over dat het de elasticity is van de ratio van a en b naar RMS.
Dus hoe is het lees
Waarin
[ Bericht 10% gewijzigd door t4rt4rus op 28-10-2014 19:59:20 ]


Je mist een min bij de MRS. MRS is een verkapte toepassing van de Implicit Function Theorem.quote:Op dinsdag 28 oktober 2014 19:26 schreef t4rt4rus het volgende:
[..]
Kom eens met de definities van MRS en EOS.
Ik kan er zo niet een goede wiskundige definitie van vinden.
Oh hier staat iets over dat het de elasticity is van de ratio van a en b naar RMS.
Dus hoe is het lees
Waarin RMS van f(x, y) gelijk is aan


Hoe los ik het volgende vraagstuk op?
Mij wordt gevraagd om de volgende integraal te berekenen:
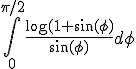
De hint die wordt gegeven is om deze integraal te berekenen via:
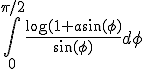
Tevens wordt als hint gegegeven om te differentiëren onder het integraalteken en om enkele substituties van trigonometrische functies te gebruiken.
Welnu, ik laat:
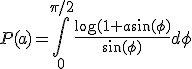
Zodat:
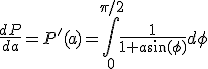
Mijn plan van aanpak is nu om hieruit een integreerbare functie te vinden, deze te integreren zodat ik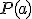 heb gevonden en dan
heb gevonden en dan 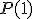 te berekenen.
te berekenen.
Deze laatste integraal kan ik echter niet oplossen, ik zie niet in welke substitutie ik hiervoor moet gebruiken.
Zou iemand me kunnen helpen?
Mij wordt gevraagd om de volgende integraal te berekenen:
De hint die wordt gegeven is om deze integraal te berekenen via:
Tevens wordt als hint gegegeven om te differentiëren onder het integraalteken en om enkele substituties van trigonometrische functies te gebruiken.
Welnu, ik laat:
Zodat:
Mijn plan van aanpak is nu om hieruit een integreerbare functie te vinden, deze te integreren zodat ik
Deze laatste integraal kan ik echter niet oplossen, ik zie niet in welke substitutie ik hiervoor moet gebruiken.
Zou iemand me kunnen helpen?


Je kunt de Weierstraß substitutie gebruiken. Stelquote:Op dinsdag 28 oktober 2014 21:17 schreef Hahatsjoe het volgende:
Hoe los ik het volgende vraagstuk op?
Mij wordt gevraagd om de volgende integraal te berekenen:
De hint die wordt gegeven is om deze integraal te berekenen via:
Tevens wordt als hint gegegeven om te differentiëren onder het integraalteken en om enkele substituties van trigonometrische functies te gebruiken.
Welnu, ik laat:
Zodat:
Mijn plan van aanpak is nu om hieruit een integreerbare functie te vinden, deze te integreren zodat ikheb gevonden en dan
te berekenen.
Deze laatste integraal kan ik echter niet oplossen, ik zie niet in welke substitutie ik hiervoor moet gebruiken.
Zou iemand me kunnen helpen?
dan is
en
zodat
Je integraal wordt dan
en deze integraal kun je in ieder geval voor 0 ≤ a < 1 gemakkelijk bepalen. Voor |a| < 1 hebben we namelijk (1 − a²) = (√(1 − a²))² zodat
een primitieve is met betrekking tot t van
en zo vinden we
Nu kunnen we deze uitdrukking voor P'(a) nog sterk vereenvoudigen door gebruik te maken van wat goniometrische identiteiten. Stellen we namelijk a = sin θ met −½π < θ < ½π, dan is
en aangezien −½π < θ < ½π is dan
Stellen we anderzijds a = cos θ met 0 < θ < π, dan is
omdat immers
en aangezien 0 < ½π − ½θ < ½π voor 0 < θ < π is dan
Nu hebben we dus
en omdat
geeft dit
en daarmee
Primitiveren geeft nu
waarmee P(0) = C terwijl we weten dat P(0) = 0 zodat C = 0 en we dus uiteindelijk krijgen
Overigens, aangezien
kunnen we ook schrijven
zodat ook
Nu is P(a) alleen gedefinieerd voor |a| < 1, maar we kunnen hier voor P(1) de limiet nemen van P(a) voor a ↑ 1 en dan hebben we P(1) = π²/8 en dus
Strict genomen moeten we nog bewijzen dat
maar dit is niet moeilijk. Met behulp van de bekende ongelijkheid 0 ≤ log(1 + x) ≤ x voor x ≥ 0 is gemakkelijk af te leiden dat we voor 0 ≤ a < 1 en 0 < φ ≤ ½π hebben
zodat het verschil tussen de integralen van log(1 + sin φ)/sinφ en log(1 + a·sin φ)/sinφ over het interval [0, ½π] niet meer bedraagt dan ½π(1 − a) en daarmee kleiner is dan een willekeurige ε > 0 voor 1 − δ < a < 1 met δ = min(2ε/π,1), QED.
[ Bericht 25% gewijzigd door Riparius op 30-10-2014 13:40:14 ]


''Elke professionele wiskundige gebruikt LaTeX'', besloot de docent zijn laatste college. Voortaan zou het handiger zijn als we onze inleveropgaves in LaTeX maken. Ik heb TeXStudio geïnstalleerd want dat raadt de studievereniging aan op haar pagina. Hun introductiecursus mis ik misschien, helaas. Waar kan ik het beste beginnen? De link in de OP is overleden.


De dingen die ik ervan weet zijn zeer beperkt. Wat ik je kan aanraden is gewoon een voorbeelddocument opzoeken. De belangrijkste dingen die je moet weten is hoe de structuur van een document in elkaar zit. Het is vooral veel googelen als je weer eens een nieuw symbool wil gebruiken. Riparius had al meer dan eens een handige site om uit te zoeken welk symbool je moet hebben gepost (als je hem zoals ik vaak gebruikt dan hoef je alleen de naam detexify in te typen en komt je browser al met de site).quote:Op donderdag 30 oktober 2014 12:16 schreef Aardappeltaart het volgende:
''Elke professionele wiskundige gebruikt LaTeX'', besloot de docent zijn laatste college. Voortaan zou het handiger zijn als we onze inleveropgaves in LaTeX maken. Ik heb TeXStudio geïnstalleerd want dat raadt de studievereniging aan op haar pagina. Hun introductiecursus mis ik misschien, helaas. Waar kan ik het beste beginnen? De link in de OP is overleden.
Hier een klein voorbeelddocument, ik neem aan dat het meeste wel te begrijpen is. Je kan het document opslaan als .tex-bestand, en kijken of je al een editor hebt (texworks staat geloof ik tegenwoordig vaak al standaaard op windows-computers).
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Toelichting:
Commando's in latex herken je door de backslash. De backslash is een zogenaamd escape-karakter. Dit betekent dat het woord achter de backslash een speciale betekenis krijgt.
In een latex-document begin je niet zomaar met de tekst die je in het document wil te typen. Je moet eerst verschillende dingen aangeven met commando's, bijvoorbeeld in welke stijl je het document wil hebben:
De bovenkant van het document is de plek om je documentclass te declareren (ik gebruik altijd article, ik weet eigenlijk niet echt alternatieven: als ik iets anders nodig heb wordt dat meestal gegeven door de docent of google ik het).
Vlak daaronder geef je door middel van het commando usepackage aan welke packages je wil gebruiken. In het voorbeeld heb ik amsfonts gebruikt. Hierin staan de N met dubbele strepen, die vaak gebruikt wordt om de verzameling natuurlijke getallen aan te geven.
Dan geef je de schrijven(author) en titel op. (Dit is geloof ik niet verplicht, maar wel zo makkelijk, omdat je dan het commando maketitle in je document kan gebruiken om zo automatisch een titel met je naam eronder te genereren).
Pas na al die dingen (Het zijn er nog veel meer als je wat beter met latex bent en wat mooiere dingen probeert te maken) kan je je daadwerkelijke document beginnen, tussen de commando's:
\begin{document} en \end{document}
Dit is overigens een vorm voor commando's die vaker voorkomt: de 'curly brackets' hebben ook een speciale betekenis: een beetje wat haakjes doen in de wiskunde: ze geven de grenzen aan waar het commando daarvoor op werkt:
a^-1 wordt a-1, a^{-1} wordt a-1 (in een formule).
Eenmaal in het document kan je section, subsection en subsubsection-commando's gebruiken om titels van de (sub)(sub)secties aan te geven. Als je geen nummer ervoor wil, kan je een aterisk gebruiken om de nummering te verbergen.
Formules zet je tussen $'s (voor inline formules) of tussen \[ en \] (voor mooie, grote, gecentreerde formules). Als je een karakter met een speciale betekenis wil gebruiken, kan je dat vaak doen door hem te escapen door er een backslash voor te zetten. (een backslash krijg je bijvoorbeeld door \\, curly brackets door \{ te gebruiken).
Voor matrix- en vectornotatie, afbeeldingen, grafen en weet ik veel wat moet je maar googelen: er is een enorm aantal mogelijkheden met latex.
[ Bericht 17% gewijzigd door defineaz op 30-10-2014 12:55:14 ]


http://ftp.snt.utwente.nl(...)/latexcourse-rug.pdfquote:Op donderdag 30 oktober 2014 12:16 schreef Aardappeltaart het volgende:
''Elke professionele wiskundige gebruikt LaTeX'', besloot de docent zijn laatste college. Voortaan zou het handiger zijn als we onze inleveropgaves in LaTeX maken. Ik heb TeXStudio geïnstalleerd want dat raadt de studievereniging aan op haar pagina. Hun introductiecursus mis ik misschien, helaas. Waar kan ik het beste beginnen? De link in de OP is overleden.
Veel plezier! Ik gebruik zelf Texmaker (en Miktex) als IDE en vind dat erg prettig werken, maar wat voor jou het beste werkt moet je zelf achter komen.


Wauw! Ik ben helemaal overdonderd door je fantastische uitwerking! Ik heb zojuist het vraagstuk zelf nogmaals opgelost en gebruikmakend van de Weierstrass-substitutie kom je inderdaad goed uit.quote:
Nu heb ik nog een lastig vraagstuk waar ik me de afgelopen dagen ook al op heb stukgebeten, en ik zou het waanzinnig appreciëren als iemand hier een sluitend bewijs voor kan vinden:
Wat kun je zeggen over de convergentie voor
Welnu mijn eerste observatie is dat p sowieso niet negatief is, anders explodeert de integrand.
Ten tweede weet ik dat ik
En dus
Welnu wat ik deed is het volgende
Intuïtief zou ik zeggen dat deze convergeert slechts dan als


Je integraal convergeert inderdaad voor 0 < p < 2, maar je argumentatie is niet deugdelijk. De clou is hier om het interval waarover je integreert op te splitsen in de intervallen [0, 1] en [1, ∞) en de convergentie over deze deelintervallen apart te bekijken. Deze vraag is al vaker voorbij gekomen op stackexchange, dus neem daar eens een kijkje.quote:Op vrijdag 31 oktober 2014 14:02 schreef Hahatsjoe het volgende:
[..]
Wauw! Ik ben helemaal overdonderd door je fantastische uitwerking! Ik heb zojuist het vraagstuk zelf nogmaals opgelost en gebruikmakend van de Weierstrass-substitutie kom je inderdaad goed uit.
Nu heb ik nog een lastig vraagstuk waar ik me de afgelopen dagen ook al op heb stukgebeten, en ik zou het waanzinnig appreciëren als iemand hier een sluitend bewijs voor kan vinden:
Wat kun je zeggen over de convergentie voorvan


We zoeken een c zodatquote:Op vrijdag 31 oktober 2014 11:23 schreef ForzaMilan het volgende:
Beste iederen: Vraagje over de normale verdeling..
[ afbeelding ]
[ afbeelding ]
Hoe komen ze op het eind nu in één keer aan die Z waarde en die 21 kranten. Tot het eind snap ik alles maar dan gaat het te snel voor me.
waar X normaal verdeeld is met mu = 25 en sigma = 5
Dit omschrijven geeft
Z = (X - mu) / sigma is standaard normaal verdeeld.
In een tabel voor de cumulative verdeling van een standaard normaalverdeling vinden we dat
Dus


Thanks!quote:Op vrijdag 31 oktober 2014 19:12 schreef Anoonumos het volgende:
[..]
We zoeken een c zodat
waar X normaal verdeeld is met mu = 25 en sigma = 5
Dit omschrijven geeft
Z = (X - mu) / sigma is standaard normaal verdeeld.
In een tabel voor de cumulative verdeling van een standaard normaalverdeling vinden we dat
Dus
Rossoneri siamo noi.


Bedankt voor je antwoord, ik zal die website onthouden!quote:Op vrijdag 31 oktober 2014 18:47 schreef Riparius het volgende:
[..]
Je integraal convergeert inderdaad voor 0 < p < 2, maar je argumentatie is niet deugdelijk. De clou is hier om het interval waarover je integreert op te splitsen in de intervallen [0, 1] en [1, ∞) en de convergentie over deze deelintervallen apart te bekijken. Deze vraag is al vaker voorbij gekomen op stackexchange, dus neem daar eens een kijkje.
Ik snap het echter nog niet helemaal, zou je je uitleg iets kunnen uitbreiden?
We zeggen dus:
En
Welke afschattingen kan ik het beste gebruiken voor deze integralen? Ik neem aan dat ik aantoon dat één van deze integralen divergeert als


Voor je laatste ongelijkheid, bedoel je niet hij divergeert alsquote:
En die integraal divergeert omdat de integrand explodeert wanneer ik
Hoe toon ik dan aan dat voor


quote:Op zondag 2 november 2014 08:38 schreef Hahatsjoe het volgende:
Hoe toon ik dan aan dat voorbeide integralen eindig zijn?
De linker helft heeft een singulariteit op x = 0.
Zoals hier boven ook al staat, convergeert deze integraal voor p < 2.
De rechter helft kan je schrijven als een alternerende serie van integralen
Met de alternerende serie test kan je dan aantonen dat deze serie convergeert voor p > 0.
http://math.stackexchange(...)nfty-frac-sinaxbxp-m
En dan krijg je als antwoord dat het integraal convergeert voor
[ Bericht 4% gewijzigd door t4rt4rus op 02-11-2014 13:13:49 ]


Het is makkelijker om dat met partieel integreren te doen in plaats van met een alternerende reeks te pielen.quote:Op zondag 2 november 2014 13:01 schreef t4rt4rus het volgende:
[..]
De rechter helft kan je schrijven als een alternerende serie van integralen
Met de alternerende serie test kan je dan aantonen dat deze serie convergeert voor p > 0.


Hier is het pielen met een alternerende serie toch heel makkelijk?quote:Op zondag 2 november 2014 13:13 schreef thabit het volgende:
[..]
Het is makkelijker om dat met partieel integreren te doen in plaats van met een alternerende reeks te pielen.
Oké
-edit-
[ Bericht 42% gewijzigd door t4rt4rus op 02-11-2014 13:59:44 ]


Het is hier inderdaad niet supermoelijk, maar het vereist meer stappen en is minder algemeen dan partieel integreren.quote:Op zondag 2 november 2014 13:54 schreef t4rt4rus het volgende:
[..]
Hier is het pielen met een alternerende serie toch heel makkelijk?
Okéhier werkt niet mee.
-edit-
[ afbeelding ]
Ter illustratie zal ik die manier hier tonen. Het punt van deze opgave is dat de integraal voor p≤1 niet absoluut convergeert. Voor p>1 doet-ie dat wel, en dat gaan we ook gebruiken.
In de limiet voor a naar oneindig convergeren beide termen aan de rechterkant: omdat p+1 > 1 en |cos x| ≤ 1, zal de rechterintegraal absoluut convergeren.


quote:Op zondag 2 november 2014 13:54 schreef t4rt4rus het volgende:
[..]
Hier is het pielen met een alternerende serie toch heel makkelijk?
Okéhier werkt niet mee.
-edit-
[ afbeelding ]
Bedankt voor jullie reacties, dat waardeer ik erg!quote:Op zondag 2 november 2014 14:12 schreef thabit het volgende:
[..]
Het is hier inderdaad niet supermoelijk, maar het vereist meer stappen en is minder algemeen dan partieel integreren.
Ter illustratie zal ik die manier hier tonen. Het punt van deze opgave is dat de integraal voor p≤1 niet absoluut convergeert. Voor p>1 doet-ie dat wel, en dat gaan we ook gebruiken.
In de limiet voor a naar oneindig convergeren beide termen aan de rechterkant: omdat p+1 > 1 en |cos x| ≤ 1, zal de rechterintegraal absoluut convergeren.
Om de integraal als alternerende serie te schrijven vind ik een verrassende truuk, en ik zal dat straks in detail bestuderen.
Wat betreft thabits uitwerking, hoe weet je nu zeker dat
Je kunt inderdaad naar de absolute convergentie kijken en dan de cosinus met 1 afschatten, maar ben je er dan? In dit geval heb je dat 0<p<2, ik zie niet in hoe dit convergentie impliceert...


Wel,quote:Op zondag 2 november 2014 18:48 schreef Hahatsjoe het volgende:
[..]
[..]
Bedankt voor jullie reacties, dat waardeer ik erg!
Om de integraal als alternerende serie te schrijven vind ik een verrassende truuk, en ik zal dat straks in detail bestuderen.
Wat betreft thabits uitwerking, hoe weet je nu zeker dat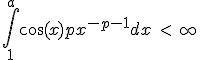
Je kunt inderdaad naar de absolute convergentie kijken en dan de cosinus met 1 afschatten, maar ben je er dan? In dit geval heb je dat 0<p<2, ik zie niet in hoe dit convergentie impliceert...
Die integraal rechts convergeert, juist omdat de integrand (minus) de afgeleide is van x-p, en x-p gaat naar 0 als x naar oneindig gaat.
Deze methode is algemeen toepasbaar op integralen van de vorm ∫f(x)g(x)dx, waarbij f(x)dx een begrensde primitieve heeft, en g(x) positief en dalend is en naar 0 convergeert. In dit voorbeeld heb je f(x)=sin(x) en g(x)=x-p.
[ Bericht 0% gewijzigd door thabit op 02-11-2014 21:13:42 ]


Goedenavond,
Ik moet het minimum en maximum van een functie bepalen gerestricteerd aan een andere functie.
E: x^2 + xy + y^2, gestricteerd aan functie G: x+y = 9. Ik denk dat ik hierbij de Extreme Value Theorem niet kan gebruiken omdat het een closed, unbounded interval is. Ik weet niet welke stap ik dan wel zou kunnen nemen om het minimum en maximum te bepalen?
Door even nadenken denk ik te kunnen zien dat het minimum 0 is, maar dat is natuurlijk niet zoals je dit probleem moet oplossen. De eerste afgeleiden helpen mij ook niet heel veel verder in deze kwestie?
Bij voorbaat dank.
Edit:
Of is het zo dat ik dan de tweede-afgeleide test voor lokale extremen moet gebruiken? Alhoewel ik dan nog met het punt zit of de waarden voor x en y in de 'interior' van het domein liggen, ik weet dus niet of de functie convex is in het gerestricteerde domein?
[ Bericht 2% gewijzigd door GivanildoVieiraDeSouza op 02-11-2014 21:12:29 ]
Ik moet het minimum en maximum van een functie bepalen gerestricteerd aan een andere functie.
E: x^2 + xy + y^2, gestricteerd aan functie G: x+y = 9. Ik denk dat ik hierbij de Extreme Value Theorem niet kan gebruiken omdat het een closed, unbounded interval is. Ik weet niet welke stap ik dan wel zou kunnen nemen om het minimum en maximum te bepalen?
Door even nadenken denk ik te kunnen zien dat het minimum 0 is, maar dat is natuurlijk niet zoals je dit probleem moet oplossen. De eerste afgeleiden helpen mij ook niet heel veel verder in deze kwestie?
Bij voorbaat dank.
Edit:
Of is het zo dat ik dan de tweede-afgeleide test voor lokale extremen moet gebruiken? Alhoewel ik dan nog met het punt zit of de waarden voor x en y in de 'interior' van het domein liggen, ik weet dus niet of de functie convex is in het gerestricteerde domein?
[ Bericht 2% gewijzigd door GivanildoVieiraDeSouza op 02-11-2014 21:12:29 ]


In dit specifieke voorbeeld kun je gewoon y=9-x invullen.quote:Op zondag 2 november 2014 20:58 schreef GivanildoVieiraDeSouza het volgende:
Goedenavond,
Ik moet het minimum en maximum van een functie bepalen gerestricteerd aan een andere functie.
E: x^2 + xy + y^2, gestricteerd aan functie G: x+y = 9. Ik denk dat ik hierbij de Extreme Value Theorem niet kan gebruiken omdat het een closed, unbounded interval is. Ik weet niet welke stap ik dan wel zou kunnen nemen om het minimum en maximum te bepalen?
Door even nadenken denk ik te kunnen zien dat het minimum 0 is, maar dat is natuurlijk niet zoals je dit probleem moet oplossen. De eerste afgeleiden helpen mij ook niet heel veel verder in deze kwestie?
Bij voorbaat dank.
Edit:
Of is het zo dat ik dan de tweede-afgeleide test voor lokale extremen moet gebruiken? Alhoewel ik dan nog met het punt zit of de waarden voor x en y in de 'interior' van het domein liggen, ik weet dus niet of de functie convex is in het gerestricteerde domein?


Als ik dit uitwerk kom ik uit op -x^2 + 9x + 81.quote:Op zondag 2 november 2014 21:14 schreef thabit het volgende:
[..]
In dit specifieke voorbeeld kun je gewoon y=9-x invullen.
De eerste afgeleide (-2x+9=0) geeft als uitkomst x=4,5 (en y is dus ook 4,5)
het punt (4,5. 4,5) is dus een globaal maximum?
En ik ben even vergeten hoe ik dan het minimum bepaal (en deze classificeer)
Bij voorbaat dank!


Als dat eruit komt en er geen verdere voorwaarden op x en y zijn (zoals x,y ≥ 0), dan zal er in dit geval geen minimum zijn.quote:Op zondag 2 november 2014 21:32 schreef GivanildoVieiraDeSouza het volgende:
[..]
Als ik dit uitwerk kom ik uit op -x^2 + 9x + 81.
De eerste afgeleide (-2x+9=0) geeft als uitkomst x=4,5 (en y is dus ook 4,5)
het punt (4,5. 4,5) is dus een globaal maximum?
En ik ben even vergeten hoe ik dan het minimum bepaal (en deze classificeer)
Bij voorbaat dank!


Je gaat hier een beetje de mist in met plusjes en minnetjes (of ik, dat kan ook). Hoe dan ook, het punt 4.5, 4.5 klopt wel weer met mijn berekeningen. Het slimste om te doen is even na te denken over hoe de grafiek eruit ziet, en dan is het wel degelijk van belang dat je de goede functie hebt.quote:Op zondag 2 november 2014 21:32 schreef GivanildoVieiraDeSouza het volgende:
[..]
Als ik dit uitwerk kom ik uit op -x^2 + 9x + 81.
De eerste afgeleide (-2x+9=0) geeft als uitkomst x=4,5 (en y is dus ook 4,5)
het punt (4,5. 4,5) is dus een globaal maximum?
En ik ben even vergeten hoe ik dan het minimum bepaal (en deze classificeer)
Bij voorbaat dank!
Een simpele test om fouten te ontdekken is om de waarden te vergelijken (het kan zijn dat hier toevallig hetzelfde uitkomt, maar de meeste fouten zal je hier wel mee ontdekken). Als je bijvoorbeeld x=1 (dus y=8) neemt, geeft jouw functie 89, terwijl de oorspronkelijke functie 73 geeft. Je bent dus ergens de fout ingegaan.


Je hebt gelijk, het is x^2 - 9x + 81. Slordige fout.quote:Op zondag 2 november 2014 21:43 schreef defineaz het volgende:
[..]
Je gaat hier een beetje de mist in met plusjes en minnetjes (of ik, dat kan ook). Hoe dan ook, het punt 4.5, 4.5 klopt wel weer met mijn berekeningen. Het slimste om te doen is even na te denken over hoe de grafiek eruit ziet, en dan is het wel degelijk van belang dat je de goede functie hebt.
Een simpele test om fouten te ontdekken is om de waarden te vergelijken (het kan zijn dat hier toevallig hetzelfde uitkomt, maar de meeste fouten zal je hier wel mee ontdekken). Als je bijvoorbeeld x=1 (dus y=8) neemt, geeft jouw functie 89, terwijl de oorspronkelijke functie 73 geeft. Je bent dus ergens de fout ingegaan.
Verder heb ik nog één vraag met betrekking tot dit onderwerp:
Ik moet het minimum en maximum van de functie f(x,y) = x^3 - xy^2 + 2y^2 -3x bepalen gerestricteerd aan de voorwaarden, H = {(x,y): x^2 + y^2 ≤ 13, x ≥ 0 en y ≥ 0. Doordat dit wel een closed, bounded interval in een continuous function is weet ik door de Extreme Value Theorem dat er een maximum en een minimum bestaat, de kandidaten hiervoor zijn stationaire punten, grenspunten en punten waarin de afgeleide niet bestaat (zijn er in deze functie niet).
De eerste afgeleide naar f'x(x,y) = 3x^2 + y^2 -3
De eerste afgeleide naar f'y(x,y) = 2yx + 4y
Ik zit vervolgens vast omdat ik niet weet hoe ik de stationaire punt(en)? moet bepalen. (Ik weet wel dat f'x(x,y) en f'y(x,y) de waarde 0 zal moeten aannemen.
Voor het bepalen van de grenspunten moet ik y^2 = 13 - x^2 in de functie invullen. Waarbij x door het interval [-√13, 13] loopt. Of maak ik hierbij ook een fout? Na dit vraagstuk zal ik jullie niet meer lastigvallen maar, alvast mijn hartelijke dank!


Wel, die twee afgeleiden gelijkstellen aan 0, en vervolgens dat stelsel proberen op te lossen.quote:Op zondag 2 november 2014 22:07 schreef GivanildoVieiraDeSouza het volgende:
[..]
Je hebt gelijk, het is x^2 - 9x + 81. Slordige fout.
Verder heb ik nog één vraag met betrekking tot dit onderwerp:
Ik moet het minimum en maximum van de functie f(x,y) = x^3 - xy^2 + 2y^2 -3x bepalen gerestricteerd aan de voorwaarden, H = {(x,y): x^2 + y^2 ≤ 13, x ≥ 0 en y ≥ 0. Doordat dit wel een closed, bounded interval in een continuous function is weet ik door de Extreme Value Theorem dat er een maximum en een minimum bestaat, de kandidaten hiervoor zijn stationaire punten, grenspunten en punten waarin de afgeleide niet bestaat (zijn er in deze functie niet).
De eerste afgeleide naar f'x(x,y) = 3x^2 + y^2 -3
De eerste afgeleide naar f'y(x,y) = 2yx + 4y
Ik zit vervolgens vast omdat ik niet weet hoe ik de stationaire punt(en)? moet bepalen. (Ik weet wel dat f'x(x,y) en f'y(x,y) de waarde 0 zal moeten aannemen.
x zal hier in het interval [-√13, √13] moeten zitten.quote:Voor het bepalen van de grenspunten moet ik y^2 = 13 - x^2 in de functie invullen. Waarbij x door het interval [-√13, 13] loopt. Of maak ik hierbij ook een fout? Na dit vraagstuk zal ik jullie niet meer lastigvallen maar, alvast mijn hartelijke dank!


Maar natuurlijk, hartstikke bedankt voor je heldere uitleg!quote:Op zondag 2 november 2014 19:22 schreef thabit het volgende:
[..]
Wel,
Die integraal rechts convergeert, juist omdat de integrand (minus) de afgeleide is van x-p, en x-p gaat naar 0 als x naar oneindig gaat.
Deze methode is algemeen toepasbaar op integralen van de vorm ∫f(x)g(x)dx, waarbij f(x)dx een begrensde primitieve heeft, en g(x) positief en dalend is en naar 0 convergeert. In dit voorbeeld heb je f(x)=sin(x) en g(x)=x-p.
Ik heb nog een laatste vraag met betrekking tot maten en Borel sigma-algebras, en dat is het volgende:
Ik heb
Nu beschouw ik de functie
Als hint staat gegeven om het gedrag te bestuderen wanneer we x vergroten.


Ik neem aan dat μ eindig moet zijn en niet σ-eindig? Anders zou μ([x,∞)) in het algemeen oneindig kunnen zijn.
Anyway, de enige eigenschap van f die je nodig hebt is dat-ie monotoon is.
[ Bericht 25% gewijzigd door thabit op 02-11-2014 23:01:57 ]
Anyway, de enige eigenschap van f die je nodig hebt is dat-ie monotoon is.
[ Bericht 25% gewijzigd door thabit op 02-11-2014 23:01:57 ]


Door dit stelsel op te lossen krijg ik x=2 en y=3 -> (2,3) is dus het enige stationaire punt. Vervolgens substitueer ik y^2 door 13 - x^2. De functie wordt dan volgensmij 2x^3 - 2x^2 - 16x + 26. De afgeleide hiervan is 6x^2 - 4x - 16. Door deze functie gelijk te stellen aan 0 kan in het stationaire punt van deze functie berekenen. Normaal zou ik het herschrijven als (x+?)(x-?) maar dat lukt me nu niet, een suggestie misschien?. De andere grenspunten zijn x = √-13 y =0 (√-13,0) en , x = √13 en y = 0 (√13,0) door alle stationaire en grenspunten vervolgens in de originele functie in te vullen vind ik het minimum en maximum.quote:Op zondag 2 november 2014 22:17 schreef thabit het volgende:
[..]
Wel, die twee afgeleiden gelijkstellen aan 0, en vervolgens dat stelsel proberen op te lossen.
[..]
x zal hier in het interval [-√13, √13] moeten zitten.


Zo staat de vraag wel in het boek, maar dat kan een drukfout zijn natuurlijk, ik heb de errata er nog niet op nageslagen.quote:Op zondag 2 november 2014 22:48 schreef thabit het volgende:
Ik neem aan dat μ eindig moet zijn en niet σ-eindig? Anders zou μ([x,∞)) in het algemeen oneindig kunnen zijn.
Als
Ik probeerde de volgende stelling te gebruiken om dit vraagstuk op te lossen; propositie 3.5 uit https://www.math.ucdavis.(...)easure_notes_ch3.pdf
Maar ik krijg het bewijs niet rond.


Goedenavond allen,
Iemand die mij met de volgende vraag m.b.t. de nutsoptimalisatie kan helpen?
Ik snap namelijk niet wat ik zou moeten doen, aangezien ik gewend ben om functies te maximaliseren a.d.h.v. de Lagrange functie waar gebruik werd gemaakt van een functie met een functievoorwaarden/functiebeperking.
Iemand die mij met de volgende vraag m.b.t. de nutsoptimalisatie kan helpen?
Ik snap namelijk niet wat ik zou moeten doen, aangezien ik gewend ben om functies te maximaliseren a.d.h.v. de Lagrange functie waar gebruik werd gemaakt van een functie met een functievoorwaarden/functiebeperking.


Jullie dictaten mogen wel eens beter op formuleringen, spelfouten en typo's worden gecontroleerd. Hint: Tom kan zijn geld maar één keer uitgeven, dus wat weet je over de betrekking tussen X, Y, Px, Py en M?quote:Op maandag 3 november 2014 19:50 schreef Super-B het volgende:
Goedenavond allen,
Iemand die mij met de volgende vraag m.b.t. de nutsoptimalisatie kan helpen?
[ afbeelding ]
Ik snap namelijk niet wat ik zou moeten doen, aangezien ik gewend ben om functies te maximaliseren a.d.h.v. de Lagrange functie waar gebruik werd gemaakt van een functie met een functievoorwaarden/functiebeperking.


Px * X = totale prijs voor goed Xquote:Op maandag 3 november 2014 20:08 schreef Riparius het volgende:
[..]
Jullie dictaten mogen wel eens beter op formuleringen, spelfouten en typo's worden gecontroleerd. Hint: Tom kan zijn geld maar één keer uitgeven, dus wat weet je over de betrekking tussen X, Y, Px, Py en M?
Py * Y = totale prijs voor goed X
Px * X + Py * Y = M
Alpha en Beta zijn constanten


Nee, voor Y. Maar dit zal een typo zijn. Zorgvuldiger je tekst controleren voordat je postquote:Op maandag 3 november 2014 21:20 schreef Super-B het volgende:
[..]
Px * X = totale prijs voor goed X
Py * Y = totale prijs voor goed X
Inderdaad. Maar er zijn verschillende problemen met de redactie van je opgave. Om te beginnen worden hier de letters X en Y gebruikt voor de namen van de twee goederen die Tom aanschaft, maar tevens voor de aantallen van elk van die goederen, en dat klopt natuurlijk al niet. Verder is de opgave strict genomen niet te beantwoorden, want het staat Tom vrij om bijvoorbeeld zijn volledige vermogen te spenderen aan uitsluitend goed X of aan uitsluitend goed Y. Maar de bedoeling is kennelijk dat Tom de nutsfunctie U(X,Y) van zijn aanschaf wil optimaliseren. Alleen had dat wel expliciet in de opgave moeten staan.quote:Px * X + Py * Y = M
Alpha en Beta zijn constanten


Hoi kan iemand hiermee helpen?
Vraag: Bereken de Relative Risk Aversion (RRA), en zeg of hij decreasing/inreasing/constant is. Met U= Y^0.5
De formule van RRA weet ik: U''/U' .
U' = 0.5Y^-0.5
U'' = -0.25Y^-1.5
Tot zo ver goed?
nouja dan kom ik dus op: (-0.25Y^-1.5) / (0.5Y^-0.5), hier stopt het voor mij kan iemand uitleggen hoe je dit kan brengen naar iets simpels, waaruit ik kan concluderen of het groeit, krimpt of constant is?
kan iemand uitleggen hoe je dit kan brengen naar iets simpels, waaruit ik kan concluderen of het groeit, krimpt of constant is?
Vraag: Bereken de Relative Risk Aversion (RRA), en zeg of hij decreasing/inreasing/constant is. Met U= Y^0.5
De formule van RRA weet ik: U''/U' .
U' = 0.5Y^-0.5
U'' = -0.25Y^-1.5
Tot zo ver goed?
nouja dan kom ik dus op: (-0.25Y^-1.5) / (0.5Y^-0.5), hier stopt het voor mij
"I never sleep, cause sleep is the cousin of death"


Mis je geen minteken in je formule?quote:Op dinsdag 4 november 2014 12:21 schreef droommoord het volgende:
Hoi kan iemand hiermee helpen?
Vraag: Bereken de Relative Risk Aversion (RRA), en zeg of hij decreasing/inreasing/constant is. Met U= Y^0.5
De formule van RRA weet ik: U''/U' .
U' = 0.5Y^-0.5
U'' = -0.25Y^-1.5
Tot zo ver goed?
nouja dan kom ik dus op: (-0.25Y^-1.5) / (0.5Y^-0.5), hier stopt het voor mijkan iemand uitleggen hoe je dit kan brengen naar iets simpels, waaruit ik kan concluderen of het groeit, krimpt of constant is?
Gebruik de rekenregel
ap / aq = ap-q


nope, in het boek staat letterlijk U''/U'quote:Op dinsdag 4 november 2014 13:02 schreef Anoonumos het volgende:
[..]
Mis je geen minteken in je formule?
Gebruik de rekenregel
ap / aq = ap-q
Ik was het al aan het proberen met die rekenregel, maar die heb ik volgens mij niet helemaal onder de knie. Ik kom uit op
(-0.25Y^-1.5) / (0.5Y^-0.5) = (-0.25/0.5)Y^-1 = -0.5Y^-1 oftewel decreasing, en dit klopt volgens het antwoorden boekje
"I never sleep, cause sleep is the cousin of death"


Maar -0.5Y^-1 is increasing.
Je uitwerking lijkt goed, maar daarom vroeg ik me af of er niet ergens een minteken hoort.
Je uitwerking lijkt goed, maar daarom vroeg ik me af of er niet ergens een minteken hoort.


Is de formule voor RRA nietquote:Op dinsdag 4 november 2014 12:21 schreef droommoord het volgende:
Hoi kan iemand hiermee helpen?
Vraag: Bereken de Relative Risk Aversion (RRA), en zeg of hij decreasing/inreasing/constant is. Met U= Y^0.5
De formule van RRA weet ik: U''/U' .
U' = 0.5Y^-0.5
U'' = -0.25Y^-1.5
Tot zo ver goed?
nouja dan kom ik dus op: (-0.25Y^-1.5) / (0.5Y^-0.5), hier stopt het voor mijkan iemand uitleggen hoe je dit kan brengen naar iets simpels, waaruit ik kan concluderen of het groeit, krimpt of constant is?
Dan kom je uit op
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |




