SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Schrijf het nog eens op, want ik heb nu geen idee waar je het over hebt.quote:Op zaterdag 13 september 2014 14:43 schreef Super-B het volgende:
[..]
Vermenigvuldigingsteken moest tussen de laatste twee grondgetallen (3).
En zet er ook eens bij welke regel je gebruikt.
Ik betwijfel of je het wel begrijpt. De vergelijking x² − 2x = 1 is niet (eenvoudig) op te lossen via ontbinden in factoren maar juist prima via kwadraatafsplitsing (die overigens altijd toepasbaar is om een vierkantsvergelijking op te lossen). Ik wil je sterk aanbevelen deze recente post van mij eens goed door te nemen.quote:
[..]
Ik beheers het kwadraat afsplitsing wel, want mij alleen verbaast is dat je het toepast bij x² - 2x = 1, aangezien de kwadraat afsplitsing meestal gebruikt wordt wanneer de c niet een goed getal is om te factoriseren (toch?).
Ik begrijp wat je wil zeggen maar zo mag je dit niet opschrijven. Je bedoelt te zeggen dat ln x = 0 equivalent is met x = 1, dus zeg dat dan ook.quote:die 1 komt omdat ln 0 is wanneer ln = 1 toch?
Een logaritme van een gegeven getal is niets anders dan een exponent, namelijk de exponent waartoe je een vast getal (het grondtal van de logaritme) moet verheffen om het gegeven getal te verkrijgen. Voor de natuurlijke logaritme, aangegeven met het functiesymbool ln (dat staat voor logarithmus naturalis) is het grondtal het bijzondere getal e. Het getal e is zo bijzonder omdat e het enige (positieve, reële) getal is waarvoor geldt dat de grafiek van f(x) = ex in elk punt precies even steil loopt als de functiewaarde voor dat punt aangeeft. De functie f(x) = ex heeft dus zichzelf als afgeleide.
De uitspraak
ln x = y
betekent niets anders dan dat y de exponent is waartoe we e moeten verheffen om x te krijgen, dus
ey = x
Zo zie je gemakkelijk dat ln 1 = 0, want 0 is immers de exponent waartoe we e moeten verheffen om 1 te krijgen: e0 = 1. Ook zie je zo gemakkelijk dat ln e = 1, want we moeten e tot de macht 1 verheffen om e te krijgen: e1 = e.
Alle rekenregels die gelden voor het werken met logaritmen volgen gemakkelijk uit de rekenregels voor het werken met machten, want een logaritme is immers niets anders dan een exponent.
Heb je bijvoorbeeld
ln a = p, ln b = q
dan betekent dit
ep = a, eq = b
Maar dan is dus ook
ep·eq = ab
En omdat exponenten optellen bij het vermenigvuldigen van twee machten met hetzelfde grondtal hebben we dus
ep+q = ab
Maar als het zo is dat je e moet verheffen tot de macht p + q om ab te krijgen, dan betekent dit niets anders dan dat de natuurlijke logaritme van ab gelijk is aan p + q, dus
ln ab = p + q
Maar nu is p = ln a en q = ln b zodat we dus hebben
ln ab = ln a + ln b
Je ziet dus dat de bekende regel die zegt dat de (natuurlijke) logaritme van een product van twee (positieve, reële) getallen gelijk is aan de som van de (natuurlijke) logaritmen van elk van de factoren niets anders is dan een andere gedaante van de regel die zegt dat exponenten optellen bij vermenigvuldiging van twee machten van hetzelfde grondtal. Op een soortgelijke manier zijn ook alle andere rekenregels voor logaritmen af te leiden uit rekenregels voor het werken met machten.
[ Bericht 0% gewijzigd door Riparius op 13-09-2014 21:50:51 ]
Dit is al fout, want je had in het rechterlid een product waar je een minteken moet hebben, maar dit zal wellicht een verschrijving zijn (die niettemin verraadt dat je niet zorgvuldig genoeg werkt).quote:
Nog één voor het oplossen van x:
4x - 4x-1 = 3x+1 - 3x
Ik heb dit herschreven tot:
4x - 4x * 4-1 = 3x * 31 - 3x
Nee jongeman, dit lijkt nergens op. Je begon nochtans goed (afgezien van die verschrijving).quote:Dit resulteert tot:
[cut crap]
Als je links een factor 4x buiten haakjes haalt en rechts een factor 3x buiten haakjes haalt dan krijg je
4x(1 − 4−1) = 3x(3 − 1)
Nu mag je eens even gaan nadenken hoe je verder kunt gaan.
Super-B, als ik jou was zou ik eens gaan inversteren in bijles of een cursus. Want je mist gewoon zoveel basiskennis. Ik weet niet welke studie je doet, maar als je zo door gaat vrees ik het ergste voor je.
Bedankt voor de tip, maar ik vind het tot nu toe vrij goed te doen met zelfstudie en dit topic.quote:
Super-B, als ik jou was zou ik eens gaan inversteren in bijles of een cursus. Want je mist gewoon zoveel basiskennis. Ik weet niet welke studie je doet, maar als je zo door gaat vrees ik het ergste voor je.
Gelukkig behoren de vragen die ik stel tot de stof van het tentamen voor volgende week en behoren ze volgens het boek tot 'harder problems'. De basic-opgaven gaan mij wel makkelijk af.
Echter is er nog veel werk te doen om de kennis goed te beheersen, maar ik denk dat het tentamen wel te doen is.De stof van het (deel)tentamen is het volgende:
De onderwerpen die ik tot nu toe nog wel pittig vind zijn:
-Logartime (niet de regels, maar de wat moeilijkere opgaven met log, ln en/of het getal e)
-Polynomen en staartdelingen.
-Afgeleiden (nieuwe materie voor mij)
-Regels voor differentiëren (ook nieuwe materie voor mij).
Inverse functies en samengestelde functies zijn ook nieuw voor mij, echter begrijp ik het tot dusverre wel.
Voor velen in dit topic is dit een eitje en zullen mijn vragen dan ook niet de moeilijkste zijn, maar het gaat tot nu toe wel goed met leren (met hier en daar nog wat slordigheidsfoutjes en wat fouten waaraan te zien is dat ik het nog niet goed beheers).
Dank voor de zéér, maar dan ook zéér duidelijke uitleg.quote:
[..]
Ik betwijfel of je het wel begrijpt. De vergelijking x² − 2x = 1 is niet (eenvoudig) op te lossen via ontbinden in factoren maar juist prima via kwadraatafsplitsing (die overigens altijd toepasbaar is om een vierkantsvergelijking op te lossen). Ik wil je sterk aanbevelen deze recente post van mij eens goed door te nemen.
[..]
Ik begrijp wat je wil zeggen maar zo mag je dit niet opschrijven. Je bedoelt te zeggen dat ln x = 0 equivalent is met x = 1, dus zeg dat dan ook.
Een logaritme van een gegeven getal is niets anders dan een exponent, namelijk de exponent waartoe je een vast getal (het grondtal van de logaritme) moet verheffen om het gegeven getal te verkrijgen. Voor de natuurlijke logaritme, aangegeven met het functiesymbool ln (dat staat voor logarithmus naturalis) is het grondtal het bijzondere getal e. Het getal e is zo bijzonder omdat e het enige (positieve, reële) getal is waarvoor geldt dat de grafiek van f(x) = ex in elk punt precies even stijl loopt als de functiewaarde voor dat punt aangeeft. De functie f(x) = ex heeft dus zichzelf als afgeleide.
De uitspraak
ln x = y
betekent niets anders dan dat y de exponent is waartoe we e moeten verheffen om x te krijgen, dus
ey = x
Zo zie je gemakkelijk dat ln 1 = 0, want 0 is immers de exponent waartoe we e moeten verheffen om 1 te krijgen: e0 = 1. Ook zie je zo gemakkelijk dat ln e = 1, want we moeten e tot de macht 1 verheffen om e te krijgen: e1 = e.
Alle rekenregels die gelden voor het werken met logaritmen volgen gemakkelijk uit de rekenregels voor het werken met machten, want een logaritme is immers niets anders dan een exponent.
Heb je bijvoorbeeld
ln a = p, ln b = q
dan betekent dit
ep = a, eq = b
Maar dan is dus ook
ep·eq = ab
En omdat exponenten optellen bij het vermenigvuldigen van twee machten met hetzelfde grondtal hebben we dus
ep+q = ab
Maar als het zo is dat je e moet verheffen tot de macht p + q om ab te krijgen, dan betekent dit niets anders dan dat de natuurlijke logaritme van ab gelijk is aan p + q, dus
ln ab = p + q
Maar nu is p = ln a en q = ln b zodat we dus hebben
ln ab = ln a + ln b
Je ziet dus dat de bekende regel die zegt dat de (natuurlijke) logaritme van een product van twee (positieve, reële) getallen gelijk is aan de som van de (natuurlijke) logaritmen van elk van de factoren niets anders is dan een andere gedaante van de regel die zegt dat exponenten optellen bij vermenigvuldiging van twee machten van hetzelfde grondtal. Op een soortgelijke manier zijn ook alle andere rekenregels voor logaritmen af te leiden uit rekenregels voor het werken met machten.
"Verschuif de lijn m over de vector p = OP→ en noem de verschoven lijn l."
Wat wordt bedoeld met verschuiven? Alleen in x/y richting verschuiven? Of ook z?.
Wat wordt bedoeld met verschuiven? Alleen in x/y richting verschuiven? Of ook z?.
Onzin, je hebt voor de zomervakantie een paar maanden lang allemaal vragen gepost over differentiëren. Weet je nog, met de ketting/product/som/quotiëntregel?quote:
[..]
Bedankt voor de tip, maar ik vind het tot nu toe vrij goed te doen met zelfstudie en dit topic.
Gelukkig behoren de vragen die ik stel tot de stof van het tentamen voor volgende week en behoren ze volgens het boek tot 'harder problems'. De basic-opgaven gaan mij wel makkelijk af.
De stof van het (deel)tentamen is het volgende:
[ afbeelding ]
De onderwerpen die ik tot nu toe nog wel pittig vind zijn:
-Logartime (niet de regels, maar de wat moeilijkere opgaven met log, ln en/of het getal e)
-Polynomen en staartdelingen.
-Afgeleiden (nieuwe materie voor mij)
-Regels voor differentiëren (ook nieuwe materie voor mij).
Inverse functies en samengestelde functies zijn ook nieuw voor mij, echter begrijp ik het tot dusverre wel.
Voor velen in dit topic is dit een eitje en zullen mijn vragen dan ook niet de moeilijkste zijn, maar het gaat tot nu toe wel goed met leren (met hier en daar nog wat slordigheidsfoutjes en wat fouten waaraan te zien is dat ik het nog niet goed beheers).
Riparius had hem ook al verteld dat hij de Spijkerreeks moet kopen, een tijd terug, of dat was tegen een andere hbo'er die ook economie wilde gaan doen. Anyhow, dat heeft diegene ook niet gedaan.quote:
Super-B, als ik jou was zou ik eens gaan inversteren in bijles of een cursus. Want je mist gewoon zoveel basiskennis. Ik weet niet welke studie je doet, maar als je zo door gaat vrees ik het ergste voor je.
Iets meer context?quote:
"Verschuif de lijn m over de vector p = OP→ en noem de verschoven lijn l."
Wat wordt bedoeld met verschuiven? Alleen in x/y richting verschuiven? Of ook z?.
Een vector is een gericht lijnstuk (of een equivalentieklasse van gerichte lijnstukken met dezelfde lengte en dezelfde richting) en een vector definieert aldus een translatie. Als je niet vertelt welke vector je vector p = OP is, dan is je vraag ook niet te beantwoorden.quote:
"Verschuif de lijn m over de vector p = OP→ en noem de verschoven lijn l."
Wat wordt bedoeld met verschuiven? Alleen in x/y richting verschuiven? Of ook z?.
quote:
Paragraaf 1.2: http://www.staff.science.(...)inalg2013dictaat.pdfquote:
[..]
Een vector is een gericht lijnstuk (of een equivalentieklasse van gerichte lijnstukken met dezelfde lengte en dezelfde richting) en een vector definieert aldus een translatie. Als je niet vertelt welke vector je vector p = OP is, dan is je vraag ook niet te beantwoorden.
Zoals ik het interpreteer in alle dimensies. De verzamelingquote:
[..]
[..]
Paragraaf 1.2: http://www.staff.science.(...)inalg2013dictaat.pdf
OK, dus als je een voorbeeld maakt, zou het er zo uit kunnen zien? https://www.dropbox.com/s(...)oorstelling.png?dl=0quote:
[..]
Zoals ik het interpreteer in alle dimensies. De verzamelingmoet je zien als alle evenwijdige lijnen van de vector
.
Teken gewoon eens een plaatje, in een plat vlak om het simpel te houden. Kies een punt O (als oorsprong) en een punt A ≠ O en teken vector OA = a, dan is elk punt op de rechte door O en A het eindpunt van een vector v = λa voor een zekere λ ∈ R, en als je λ de verzameling R van alle reële getallen laat doorlopen dan krijg je voor het eindpunt van vector v = λa elk punt op de rechte door O en A. We noemen v = λa daarom een vectorvoorstelling van de rechte m door O en A.quote:
[..]
[..]
Paragraaf 1.2: http://www.staff.science.(...)inalg2013dictaat.pdf
Kies vervolgens een willekeurig punt P buiten lijn m en verschuif lijn m dan in één rechte beweging zodanig dat punt O op lijn m in punt P komt te liggen. Dan hebben we als beeld van de rechte lijn m een rechte lijn l door punt P die evenwijdig is aan lijn m. Elk punt op deze lijn l is nu het eindpunt van een vector v = p + λa voor een zekere λ ∈ R, en als je λ weer de verzameling R van alle reële getallen laat doorlopen dan krijg je als eindpunt van vector v = p + λa elk punt op de rechte l door P evenwijdig aan m. Aldus is v = p + λa een vectorvoorstelling van l. Vector a heet een richtingsvector van lijn l en vector p heet een steunvector (ook wel een plaatsvector) van lijn l.
Vóór de zomervakantie. Dat was voor de toelatingstoets wiskunde voor de universiteit. Heb het afgerond met een 7.0. Desondanks blijt de materie nog nieuw voor mij. Het is alweer weggezakt en havo/hbo wiskunde stelt niet zoveel voor.quote:
[..]
Onzin, je hebt voor de zomervakantie een paar maanden lang allemaal vragen gepost over differentiëren. Weet je nog, met de ketting/product/som/quotiëntregel?
Als ik (e0,001 - 1) / 1 invul in mijn rekenmachine krijg ik geen , maar 0,0010005 Doe ik iets fout of..?
Je deelt door 1 ipv x.quote:
[ afbeelding ]
Als ik (e0,001 - 1) / 1 invul in mijn rekenmachine krijg ik geen [ afbeelding ], maar 0,0010005 Doe ik iets fout of..?
Ja, je doet iets fout, en in mijn glazen bol zie ik dat je waarschijnlijk alleen ex − 1 hebt berekend voor x = 0,001. Je bent dus helemaal vergeten dat je het resultaat weer door x moest delen.quote:
[ afbeelding ]
Als ik (e0,001 - 1) / 1 invul in mijn rekenmachine krijg ik geen [ afbeelding ], maar 0,0010005 Doe ik iets fout of..?
quote:
Slordig!quote:
[..]
Ja, je doet iets fout, en in mijn glazen bol zie ik dat je waarschijnlijk alleen ex hebt berekend voor x = 0,001. Je bent dus helemaal vergeten dat je van die ex nog 1 af moest trekken en het resultaat weer door x moest delen.
Thanks!
Wiskunde is echt een heerlijk vak, met name door de uitdaging die er in zit.
Hopelijk zie je ook waarom die limiet van (ex − 1)/x voor x → 0 oftewel de limiet van (eh − 1)/h voor h → 0 nu zo interessant is. Als je de afgeleide gaat bepalen vanquote:
[..]
[..]
Wiskunde is echt een heerlijk vak, met name door de uitdaging die er in zit.
f(x) = ax
voor een a ∈ R+ met behulp van de definitie van de afgeleide, dan krijg je
f'(x) = limh→0 (ax+h − ax)/h
en aangezien ax+h = ax·ah kunnen we een factor ax buiten haakjes halen in de teller van het differentiequotiënt en omdat ax niet afhangt van h kunnen we deze factor ax voor de limiet brengen zodat we kunnen schrijven
f'(x) = ax · limh→0 (ah − 1)/h
Maar omdat 1 = a0 is limh→0 (ah − 1)/h = limh→0 (ah − a0)/h niets anders dan de afgeleide van de functie in het punt x = 0 oftewel f'(0). We vinden voor de functie f(x) = ax dus
f'(x) = f'(0)·ax
Een exponentiële functie heeft dus een afgeleide die weer een exponentiële functie is met datzelfde grondtal, maar dan wel vermenigvuldigd met een constante factor die de steilheid geeft van de grafiek van de functie bij x = 0. En nu blijkt er precies één positief reëel getal a te zijn waarbij de steilheid van de exponentiële curve bij x = 0 precies gelijk is aan 1, en dat getal noemen we e. Voor a = e heb je zo dus
f'(x) = ex
als afgeleide van
f(x) = ex
Natuurlijk wil je nu ook nog weten wat die f'(0) = limh→0 (ah − 1)/h voor een willekeurige (positieve, reële) a nu in het algemeen voorstelt, en dat blijkt niets anders te zijn dan de natuurlijke logaritme van a, dus
limh→0 (ah − 1)/h = ln a
Zo hebben we dus voor
f(x) = ax
met a ∈ R+ in het algemeen als afgeleide
f'(x) = ax·ln a
Okay volgens mij is dit redelijk simpel maar ik zie het gewoon niet, ik hoop dat iemand mij kan helpen.
Is de som: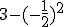
hetzelfde als: 
?
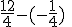Naar mijn inzien namelijk wel maar de antwoorden verschillen. het antwoord van som 1 is namelijk 2,75 en die van som twee 3,25.
Is de som:
Naar mijn inzien namelijk wel maar de antwoorden verschillen. het antwoord van som 1 is namelijk 2,75 en die van som twee 3,25.
Nee, dit is niet hetzelfde. Je negeert namelijk de rekenregel min maal min geeft plus. Het kwadraat van −½ is ¼, niet −¼.quote:
Okay volgens mij is dit redelijk simpel maar ik zie het gewoon niet, ik hoop dat iemand mij kan helpen.
Is de som:
Naar mijn inzien namelijk wel maar de antwoorden verschillen. het antwoord van som 1 is namelijk 2,75 en die van som twee 3,25.
Aaah, danku! Al te lang achter elkaar bezig denk ikquote:
[..]
Nee, dit is niet hetzelfde. Je negeert namelijk de rekenregel min maal min geeft plus. Het kwadraat van −½ is ¼, niet −¼.
Vermenigvuldig je die - die rechts van de drie staat niet eerst met een deel v/h kwadraat?quote:
[..]
Nee, dit is niet hetzelfde. Je negeert namelijk de rekenregel min maal min geeft plus. Het kwadraat van −½ is ¼, niet −¼.
Dus 3 - (-1/2)^2 is 3 - (-1/2) * (-1/2) en dus
3 + (1/2) * (-1/2) ?
Zo niet, waarom niet
Zo zou je het ook kunnen zien ja. Het punt was voornamelijk dat je uiteindelijk een minteken overhoudt. In welke volgorde je de twee andere mintekens vermenigvuldigt maakt niets uit.quote:Op zondag 14 september 2014 17:25 schreef Super-B het volgende:
[..]
Vermenigvuldig je die - die rechts van de drie staat niet eerst met een deel v/h kwadraat?
Dus 3 - (-1/2)^2 is 3 - (-1/2) * (-1/2) en dus
3 + (1/2) * (-1/2) ?
Zo niet, waarom niet
Jij neemt een van de mintekens in het kwadraat en haalt die naar buiten, terwijl Riparius (-1/2)2 = +1/4 doet.
Ik heb nog een vraag, ditmaal over de afgeleide/het differentiëren.
Stel je hebt de raaklijn berekent ofwel de afgeleide van een functie. Wat houdt dat dan in? Stel je afgeleide is
y = x², wat kun je daar dan mee? Ik heb verschillende video's bekeken en dan wordt er gesproken over het richtingscoëfficiënt berekenen van 'dat' punt oid, maar kan dat ook van elk punt, ook waar de raaklijn niet de gewone functie snijdt (zoals het standaard is dat de raaklijn door twee punten snijdt met de gewone functie)?
Wat de richtingscoëfficiënt is, is mij wel duidelijk; dat bepaalt de richting van de lijn bij elke x-stap. Echter is de afgeleide mij nog wat wazig, ondanks het bekijken van verschillende video's.
Het is niet zozeer dat ik de methodiek lastig vind, maar de achtergrond van de afgeleide niet begrijp.
Stel je hebt de raaklijn berekent ofwel de afgeleide van een functie. Wat houdt dat dan in? Stel je afgeleide is
y = x², wat kun je daar dan mee? Ik heb verschillende video's bekeken en dan wordt er gesproken over het richtingscoëfficiënt berekenen van 'dat' punt oid, maar kan dat ook van elk punt, ook waar de raaklijn niet de gewone functie snijdt (zoals het standaard is dat de raaklijn door twee punten snijdt met de gewone functie)?
Wat de richtingscoëfficiënt is, is mij wel duidelijk; dat bepaalt de richting van de lijn bij elke x-stap. Echter is de afgeleide mij nog wat wazig, ondanks het bekijken van verschillende video's.
Het is niet zozeer dat ik de methodiek lastig vind, maar de achtergrond van de afgeleide niet begrijp.
De afgeleide functie geeft de steilheid van de grafiek van de oorspronkelijke functie in elk punt op de grafiek van die oorspronkelijke functie. De afgeleide functie geeft zo dus informatie over het verloop van de grafiek van de oorspronkelijke functie. Je kunt deze informatie (dus: de afgeleide functie) zo gebruiken om bijvoorbeeld (locale en globale) maxima en minima van de oorspronkelijke functie op te sporen. Dit is vaak belangrijk bij allerlei praktische vraagstukken. In de economie wil je bijvoorbeeld kunnen bestuderen hoe de winst afhangt van allerlei variabelen en hoe je die winst kunt maximaliseren.quote:
Ik heb nog een vraag, ditmaal over de afgeleide/het differentiëren.
Stel je hebt de raaklijn berekend ofwel de afgeleide van een functie. Wat houdt dat dan in? Stel je afgeleide is
y = x², wat kun je daar dan mee?
Aha.. stel hé ik vul een x-punt van de gewone functie (2) in de afgeleide 2x in.. (de betreffende punt is 2,4). Dan heb jequote:
[..]
De afgeleide functie geeft de steilheid van de grafiek van de oorspronkelijke functie in elk punt op de grafiek van die oorspronkelijke functie. De afgeleide functie geeft zo dus informatie over het verloop van de grafiek van de oorspronkelijke functie. Je kunt deze informatie (dus: de afgeleide functie) zo gebruiken om bijvoorbeeld (locale en globale) maxima en minima van de oorspronkelijke functie op te sporen. Dit is vaak belangrijk bij allerlei praktische vraagstukken. In de economie wil je bijvoorbeeld kunnen bestuderen hoe de winst afhangt van allerlei variabelen en hoe je die winst kunt maximaliseren.
2*2 = 4, wat zegt die 4 dan? Dat het richtingscoëfficiënt is op dat x-punt en je zodoende een functie kan maken van het x-punt 2. Dus in dat geval
y = ax + b
y = 4x + b
4 = 4*2 + b
4 = 8 + b
-4 = b
Dus de functie op punt (2,4) is dan y = 4x - 4 toch?
P.s; kan de afgeleide ook op lineaire functies toegepast worden of alleen functies welke een grafiek hebben waarvan de richtingscoëfficiënt op elk punt anders is (bijv. doordat de grafiek een gebogen grafiek is)?
Nee, nu bepaal je de y-waarde die bij een bepaalde x-waarde hoort. De afgeleide van f(x) = x2 is f'(x) = 2x.quote:
[..]
Aha.. stel hé ik vul een x-punt van de gewone functie (2) in de afgeleide x² in.. (de betreffende punt is 2,4). Dan heb je
2² = 4, wat zegt die 4 dan? Dat het richtingscoëfficiënt is op dat x-punt en je zodoende een functie kan maken van het x-punt 2. Dus in dat geval
y = ax + b
y = 4x + b
4 = 4*2 + b
4 = 8 + b
-4 = b
Dus de functie op punt (2,4) is dan y = 4x - 4 toch?
P.s; kan de afgeleide ook op lineaire functies toegepast worden of alleen functies welke een grafiek hebben waarvan de richtingscoëfficiënt op elk punt anders is (bijv. doordat de grafiek een gebogen grafiek is)?
Zie edit. Gelukkig maakt het voor de berekening even niets uit, aangezien 2*2 hetzelfde is als 2². Dus ik heb niet veel hoeven te editen.quote:
[..]
Nee, nu bepaal je de y-waarde die bij een bepaalde x-waarde hoort. De afgeleide van f(x) = x2 is f'(x) = 2x.
Deze kromme formulering geeft mooi je verwarring weer. Je moet wel onderscheid maken tussen een snijlijn door twee punten op de grafiek (die meestal dicht bij elkaar worden gekozen) en een raaklijn in één punt van de grafiek.quote:
Ik heb nog een vraag, ditmaal over de afgeleide/het differentiëren.
Stel je hebt de raaklijn berekent ofwel de afgeleide van een functie. Wat houdt dat dan in? Stel je afgeleide is
y = x², wat kun je daar dan mee? Ik heb verschillende video's bekeken en dan wordt er gesproken over het de richtingscoëfficiënt berekenen van 'dat' punt o.i.d., maar kan dat ook van elk punt, ook waar de raaklijn niet de gewone functie snijdt (zoals het standaard is dat de raaklijn door twee punten snijdt met de gewone functie)?
Je kunt het je zo voorstellen dat je één punt op je grafiek kiest en daarnaast nog een tweede punt op de grafiek daar dicht bij. Omdat een rechte lijn volledig vastligt door twee punten, kun je nu door die twee punten precies één rechte lijn trekken. Laat je nu het tweede punt op de grafiek naar het eerste punt toe kruipen, en wel langs de grafiek, dan zal de snijlijn door de twee punten steeds meer de richting krijgen van de raaklijn aan dat eerste punt op de grafiek.
De steilheid ofwel de richtingscoëfficiënt van de snijlijn door twee punten (x, f(x)) en (x+h, f(x+h)) op de grafiek van een functie f bereken je door het verschil in verticale positiequote:Wat de richtingscoëfficiënt is, is mij wel duidelijk; dat bepaalt de richting van de lijn bij elke x-stap. Echter is de afgeleide mij nog wat wazig, ondanks het bekijken van verschillende video's.
Het is niet zozeer dat ik de methodiek lastig vind, maar de achtergrond van de afgeleide niet begrijp.
Δy = f(x+h) − f(x)
tussen de twee punten (x, f(x)) en (x+h, f(x+h)) te delen door het verschil in horizontale positie
Δx = (x+h) − x = h
van de twee punten. Zo krijgen we voor de steilheid van onze snijlijn door de twee punten (x, f(x)) en (x+h, f(x+h)) op de grafiek van onze functie f dus
Δy/Δx = (f(x+h) − f(x))/h
Maar nu zijn we niet geïnteresseerd in de steilheid van de snijlijn door de punten (x, f(x)) en (x+h, f(x+h)) op de grafiek van f, maar in de steilheid van de grafiek van f zelf in dat ene punt (x, f(x)) op de grafiek. En die steilheid is niets anders dan de steilheid van de raaklijn aan de grafiek van f in dit punt (x, f(x)). Wat we dus moeten doen is die waarde van h naar nul laten gaan zodat het tweede punt (x+h, f(x+h)) langs de grafiek naar het eerste punt (x, f(x)) gaat, want dan gaat de steilheid van de snijlijn steeds meer in de buurt komen van de steilheid van de raaklijn aan de grafiek in het punt (x, f(x)) waar we eigenlijk in zijn geïnteresseerd.
Maar nu hebben we een probleem, want we kunnen in
Δy/Δx = (f(x+h) − f(x))/h
niet zomaar h = 0 invullen want dan wordt Δy = 0 en ook Δx = 0 zodat de breuk 0/0 wordt, en dat heeft geen betekenis. Daarom moeten we gaan kijken wat er gebeurt als we dat verschil h in horizontale positie tussen de twee punten op de grafiek niet nul maken maar wel heel dicht (willekeurig dicht) tegen 0 aan laten kruipen. Hierbij moet je nog bedenken dat h niet positief hoeft te zijn, want we kunnen h ook vanaf de negatieve kant tegen 0 aan laten kruipen.
Wat we hier eigenlijk nodig hebben is het begrip limiet. Een limiet is niets anders dan een grenswaarde waarbij we zo dicht in de buurt kunnen komen als we maar willen, als we een bepaalde variabele (hier: h) maar dicht genoeg bij een bepaalde waarde (hier: 0) kiezen. En die limiet van bovenstaande uitdrukking (f(x+h) − f(x))/h voor h → 0 is zo niets anders dan de steilheid van de raaklijn aan de grafiek in het punt (x, f(x)) oftewel de afgeleide f'(x), dus
f'(x) = limh→0 (f(x+h) − f(x))/h
Nu zou het heel omslachtig zijn als we altijd maar weer zo'n limiet moesten gaan bepalen om een afgeleide functie te vinden, maar dat hoeft niet. Want voor allerlei 'standaardfuncties' is het mogelijk om eens en voor altijd aan de hand van deze limiet te bepalen wat de afgeleide is, en als we dat eenmaal weten dan kunnen we daar verder gewoon mee werken. Zo kan men bijvoorbeeld aan de hand van deze limiet bewijzen dat voor
f(x) = xn
geldt
f'(x) = nxn−1
Behalve een aantal afgeleiden voor 'standaardfuncties' zijn er ook nog regels voor het bepalen van de afgeleide functie van bijvoorbeeld de som, het verschil, het product, of het quotiënt van twee gegeven functies, en ook die regels zijn allemaal te bewijzen aan de hand van bovenstaande definitie van de afgeleide. Tenslotte is het ook belangrijk om de afgeleide te kunnen bepalen van een samenstelling van twee (of meer) functies waarbij de 'output' van de eerste functie dient als 'input' voor de tweede functie. Dat is de kettingregel, en ook die is uiteraard te bewijzen aan de hand van bovenstaande definitie van de afgeleide.
[ Bericht 0% gewijzigd door Riparius op 14-09-2014 23:49:15 ]
Wat heb je geprobeerd? Welke rekenregels ken je?quote:
Waarom is 5 / 2sqrt5 = (1/2)sqrt5 ?
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Vermenigvuldig teller en noemer van je breuk met √5, dan heb jequote:
Waarom is 5 / 2sqrt5 = (1/2)sqrt5 ?
Hartstikke duidelijk. Enorm bedankt.quote:
[..]
Deze kromme formulering geeft mooi je verwarring weer. Je moet wel onderscheid maken tussen een snijlijn door twee punten op de grafiek (die meestal dicht bij elkaar worden gekozen) en een raaklijn in één punt van de grafiek.
Je kunt het je zo voorstellen dat je één punt op je grafiek kiest en daarnaast nog een tweede punt op de grafiek daar dicht bij. Omdat een rechte lijn volledig vastligt door twee punten, kun je nu door die twee punten precies één rechte lijn trekken. Laat je nu het tweede punt op de grafiek naar het eerste punt toe kruipen, en wel langs de grafiek, dan zal de snijlijn door de twee punten steeds meer de richting krijgen van de raaklijn aan dat eerste punt op de grafiek.
[..]
De steilheid ofwel de richtingscoëfficiënt van de snijlijn door twee punten (x, f(x)) en (x+h, f(x+h)) op de grafiek van een functie f bereken je door het verschil in verticale afstand
Δy = f(x+h) − f(x)
tussen de twee punten (x, f(x)) en (x+h, f(x+h)) te delen door het verschil in horizontale afstand
Δx = (x+h) − x = h
van de twee punten. Zo krijgen we voor de steilheid van onze snijlijn door de twee punten (x, f(x)) en (x+h, f(x+h)) op de grafiek van onze functie f dus
Δy/Δx = (f(x+h) − f(x))/h
Maar nu zijn we niet geïnteresseerd in de steilheid van de snijlijn door de punten (x, f(x)) en (x+h, f(x+h)) op de grafiek van f, maar in de steilheid van de grafiek van f zelf in dat ene punt (x, f(x)) op de grafiek. En die steilheid is niets anders dan de steilheid van de raaklijn aan de grafiek van f in dit punt (x, f(x)). Wat we dus moeten doen is die waarde van h naar nul laten gaan zodat het tweede punt (x+h, f(x+h)) langs de grafiek naar het eerste punt (x, f(x)) gaat, want dan gaat de steilheid van de snijlijn steeds meer in de buurt komen van de steilheid van de raaklijn aan de grafiek in het punt (x, f(x)) waar we eigenlijk in zijn geïnteresseerd.
Maar nu hebben we een probleem, want we kunnen in
Δy/Δx = (f(x+h) − f(x))/h
niet zomaar h = 0 invullen want dan wordt Δy = 0 en ook Δx = 0 zodat de breuk 0/0 wordt, en dat heeft geen betekenis. Daarom moeten we gaan kijken wat er gebeurt als we dat verschil h in horizontale afstand tussen de twee punten op de grafiek niet nul maken maar wel heel dicht (willekeurig dicht) tegen 0 aan laten kruipen. Hierbij moet je nog bedenken dat h niet positief hoeft te zijn, want we kunnen h ook vanaf de negatieve kant tegen 0 aan laten kruipen.
Wat we hier eigenlijk nodig hebben is het begrip limiet. Een limiet is niets anders dan een grenswaarde waarbij we zo dicht in de buurt kunnen komen als we maar willen, als we een bepaalde variabele(hier: h) maar dicht genoeg bij een bepaalde waarde (hier: 0) kiezen. En die limiet van bovenstaande uitdrukking (f(x+h) − f(x))/h voor h → 0 is zo niets anders dan de steilheid van de raaklijn aan de grafiek in het punt (x, f(x)) oftewel de afgeleide f'(x), dus
f'(x) = limh→0(f(x+h) − f(x))/h
Nu zou het heel omslachtig zijn als we altijd maar weer zo'n limiet moesten gaan bepalen om een afgeleide functie te vinden, maar dat hoeft niet. Want voor allerlei 'standaardfuncties' is het mogelijk om eens en voor altijd aan de hand van deze limiet te bepalen wat de afgeleide is, en als we dat eenmaal weten dan kunnen we daar verder gewoon mee werken. Zo kan men bijvoorbeeld aan de hand van deze limiet bewijzen dat voor
f(x) = xn
geldt
f'(x) = nxn−1
Behalve een aantal afgeleiden voor 'standaardfuncties' zijn er ook nog regels voor het bepalen van de afgeleide functie van bijvoorbeeld de som, het verschil, het product, of het quotiënt van twee gegeven functies, en ook die regels zijn allemaal te bewijzen aan de hand van bovenstaande definitie van de afgeleide. Tenslotte is het ook belangrijk om de afgeleide te kunnen bepalen van een samenstelling van twee (of meer) functies waarbij de 'output' van de eerste functie dient als 'input' voor de tweede functie. Dat is de kettingregel, en ook die is uiteraard te bewijzen aan de hand van bovenstaande definitie van de afgeleide.
Echter is mij dus dan nog steeds niet duidelijk wat ik dan precies met de afgeleide kan doen..
Stel de functie y = 2x² heeft de afgeleide y = 4x. Wat kan ik dan allemaal met die afgeleiden? Welke x moet ik dan invullen en wat kun je dan met de y die eruit rolt? Kun je zomaar alle punten invullen van de gewone functie in de afgeleide?
Kun je dan zomaar de coördinaten van de gewone functie pakken van (8,3) en wat levert het op etc etc.. Ik weet dat het betreft om de steilheid, maar praktiserend begrijp ik het dus niet..
Stel je hebt s = 5t2 (s is de verplaatsing in de natuurkunde). Dan is s' = 10t. De snelheid op het punt t = 5 is dan 50 m/s.quote:
[..]
Hartstikke duidelijk. Enorm bedankt.
Echter is mij dus dan nog steeds niet duidelijk wat ik dan precies met de afgeleide kan doen..
Stel de functie y = 2x² heeft de afgeleide y = 4x. Wat kan ik dan allemaal met die afgeleiden? Welke x moet ik dan invullen en wat kun je dan met de y die eruit rolt? Kun je zomaar alle punten invullen van de gewone functie in de afgeleide?
Kun je dan zomaar de coördinaten van de gewone functie pakken van (8,3) en wat levert het op etc etc.. Ik weet dat het betreft om de steilheid, maar praktiserend begrijp ik het dus niet..
[ afbeelding ]
Dit is een voorbeeld, maar dit kan je op alles toepassen dat te maken heeft met een verandering. Die verandering kan je dan oneindig klein maken (het limiet -> 0), waardoor je de verandering op dat punt krijgt.
Differentiëren is ook heel nuttig bij optimalisatie. Als je wil kijken waar de functie een maximum heeft, dan moet daar gelden dat de afgeleide nul is (best "logisch" als je daar even over nadenkt!).
Door de afgeleide gelijk aan nul te stellen kun je dus (lokale) maxima en minima van de functie vinden. In de praktijk kan het van alles zijn wat je probeert te maximaliseren. Denk bijvoorbeeld aan winstmaximalisatie.
Door de afgeleide gelijk aan nul te stellen kun je dus (lokale) maxima en minima van de functie vinden. In de praktijk kan het van alles zijn wat je probeert te maximaliseren. Denk bijvoorbeeld aan winstmaximalisatie.
Dit is wel een erg eenvoudig voorbeeld. Als je hebt f(x) = 2x2 dan is inderdaad f'(x) = 4x. Je ziet dan bijvoorbeeld dat f'(x) = 0 uitsluitend als x = 0. Zo weet je dus dat de raaklijn aan de grafiek van f(x) = 2x² alleen horizontaal loopt in het punt (0, 0) op de grafiek, en dat betekent dat f(x) = 2x² een extreme waarde bereikt voor x = 0, en wel een minimum van f(0) = 0. Maar dat wist je al omdat het kwadraat van een reëel getal niet negatief kan zijn, dus dit is niet zo spannend.quote:
[..]
Hartstikke duidelijk. Enorm bedankt.
Echter is mij dus dan nog steeds niet duidelijk wat ik dan precies met de afgeleide kan doen..
Stel de functie y = 2x² heeft de afgeleide y = 4x. Wat kan ik dan allemaal met die afgeleiden?
Maar laten we eens naar de algemene kwadratische functie
f(x) = ax² + bx + c
kijken, waarbij a,b,c concrete getallen voorstellen en a niet nul mag zijn omdat je anders geen kwadratische term meer zou hebben. Als we hier de afgeleide functie bepalen, dan krijgen we
f'(x) = 2ax + b
en als nu f'(x) = 0 moet zijn, dan moet dus gelden
2ax + b = 0
en dus
2ax = −b
en dus
x = −b/2a
Zo zie je dus dat de kwadratische functie f(x) = ax² + bx + c een extreme waarde bereikt voor x = −b/2a. Het is ook mogelijk dit resultaat te vinden door elementaire herleiding (kwadraatafsplitsing, zie bijvoorbeeld hier) maar met differentiaalrekening gaat het veel eenvoudiger. Bovendien kunnen we de differentiaalrekening ook gebruiken bij allerlei andere functies waarbij maxima en minima niet meer met elementaire algebraïsche foefjes zijn te vinden. Zo zie je dus dat de differentiaalrekening een heel krachtig hulpmiddel is bij het onderzoeken van het gedrag van allerlei functies.
Bij het soort functies waarmee je nu te maken hebt is dit vaak wel het geval, maar niet altijd. Het hoeft namelijk niet zo te zijn dat je oorspronkelijke functie ook voor alle waarden van x uit het domein differentieerbaar is.quote:Welke x moet ik dan invullen en wat kun je dan met de y die eruit rolt? Kun je zomaar alle punten invullen van de gewone functie in de afgeleide?
Het plaatje dat je geeft is een mooi voorbeeld van een functie die niet differentieerbaar is in het punt x = 0. Kun je ook tenminste één of mogelijk twee redenen geven waarom dat zo is?quote:Kun je dan zomaar de coördinaten van de gewone functie pakken van (8,3) en wat levert het op etc etc.. Ik weet dat het betreft om de steilheid, maar praktiserend begrijp ik het dus niet..
[ afbeelding ]
[ Bericht 1% gewijzigd door Riparius op 14-09-2014 19:39:55 ]
Dank voor alweer een zeer duidelijke uitleg!quote:
[..]
Dit is wel een erg eenvoudig voorbeeld. Als je hebt f(x) = 2x2 dan is inderdaad f'(x) = 4x. Je ziet dan bijvoorbeeld dat f'(x) = 0 uitsluitend als x = 0. Zo weet je dus dat de raaklijn aan de grafiek van f(x) = 2x² alleen horizontaal loopt in het punt (0, 0) op de grafiek, en dat betekent dat f(x) = 2x² een extreme waarde bereikt voor x = 0, en wel een minimum van f(0) = 0. Maar dat wist je al omdat het kwadraat van een reëel getal niet negatief kan zijn, dus dit is niet zo spannend.
Maar laten we eens naar de algemene kwadratische functie
f(x) = ax² + bx + c
kijken, waarbij a,b,c concrete getallen voorstellen en a niet nul mag zijn omdat je anders geen kwadratische term meer zou hebben. Als we hier de afgeleide functie bepalen, dan krijgen we
f'(x) = 2ax + b
en als nu f'(x) = 0 moet zijn, dan moet dus gelden
2ax + b = 0
en dus
2ax = −b
en dus
x = −b/2a
Zo zie je dus dat de kwadratische functie f(x) = ax² + bx + c een extreme waarde bereikt voor x = −b/2a. Het is ook mogelijk dit resultaat te vinden door elementaire herleiding (kwadraatafsplitsing, zie bijvoorbeeld hier) maar met differentiaalrekening gaat het veel eenvoudiger. Bovendien kunnen we de differentiaalrekening ook gebruiken bij allerlei andere functies waarbij maxima en minima niet meer met elementaire algebraïsche foefjes zijn te vinden. Zo zie je dus dat de differentiaalrekening een heel krachtig hulpmiddel is bij het onderzoeken van het gedrag van allerlei functies.
[..]
Bij het soort functies waarmee je nu te maken hebt is dit vaak wel het geval, maar niet altijd. Het hoeft namelijk niet zo te zijn dat je oorspronkelijke functie ook voor alle waarden van x uit het domein differentieerbaar is.
[..]
Het plaatje dat je geeft is een mooi voorbeeld van een functie die niet differentieerbaar is in het punt x = 0. Kun je ook tenminste één of mogelijk twee redenen geven waarom dat zo is?
Nee ik kan me niet bedenken waarom.
Hebben deze functies een standaard naam?
Bedankt alvast.
| 1 2 3 | phi1(z) = ( exp(z) - 1 ) / z phi2(z) = ( phi1(z) - 1 ) / z |
Bedankt alvast.
gr gr
Ik moet zeggen dat het boek 'Essential Mathematics for Economic Analysis' een veel duidelijkere boek is dan het 'Basisboek Wiskunde' van Jan van Craats. 
Na het lezen van ieder hoofdstuk uit het basisboek had ik toch veel vraagtekens overgehouden i.t.t. wanneer ik een hoofdstuk uit het boek Mathematics for Economic Analysis gelezen heb (in ieder geval minder vraagtekens).
Na het lezen van ieder hoofdstuk uit het basisboek had ik toch veel vraagtekens overgehouden i.t.t. wanneer ik een hoofdstuk uit het boek Mathematics for Economic Analysis gelezen heb (in ieder geval minder vraagtekens).
'Show that f(x) = x^3 is strictly increasing. "
Nou allereerst moet ik de afgeleide bepalen en dat is 3x^2, maar vervolgens loop ik vast.. want er staat een hint waar ik een bepaalde sign moet gebruiken welke ik eerder niet heb gezien:
Hint: consider the sign of x(3/2) - (3/2) = (x2 - x1)(x2/1 + x1x2 + x 2/2)
Die deelstrepen behoren er niet want het is volgens mij geen breuk.
Nou allereerst moet ik de afgeleide bepalen en dat is 3x^2, maar vervolgens loop ik vast.. want er staat een hint waar ik een bepaalde sign moet gebruiken welke ik eerder niet heb gezien:
Hint: consider the sign of x(3/2) - (3/2) = (x2 - x1)(x2/1 + x1x2 + x 2/2)
Die deelstrepen behoren er niet want het is volgens mij geen breuk.
Kijk nog eens naar de grafiek die je gaf bij je vorige post. Dit is de grafiek van de functiequote:
[..]
Dank voor alweer een zeer duidelijke uitleg!
Nee ik kan me niet bedenken waarom.
f(x) = √x
Deze functie is alleen gedefinieerd voor x ≥ 0 oftewel op het interval [0, ∞), want √x is binnen R (de verzameling van alle reële getallen) niet gedefinieerd als x negatief is.
Bij x = 0 zitten we dus op de rand van het domein van deze functie, en je ziet ook dat de grafiek hier 'begint' (of 'stopt', zo je wil). Maar dit betekent dat deze functie niet differentieerbaar is voor x = 0. Waarom niet? Wel dat volgt om te beginnen uit de definitie van de afgeleide:
We moeten hier h naar nul kunnen laten gaan niet alleen vanaf de positieve kant, maar ook vanaf de negatieve kant, en het differentiequotiënt moet dan naderen tot dezelfde grenswaarde, en dat is dan de limiet van dit differentiequotiënt voor h → 0 oftewel de afgeleide. Als we de afgeleide voor x = 0 oftewel f'(0) willen bepalen dan hebben we volgens deze definitie
Maar nu zie je het probleem: f(h) is niet gedefinieerd voor enige h < 0, en dus bestaat deze limiet niet. Het is niet noodzakelijk dat f(h) is gedefinieerd voor elke h als we f'(0) willen bepalen, maar f(h) moet in ieder geval wel zijn gedefinieerd voor elke h in een omgeving van 0 en dat is hier niet het geval.
Nu zou je nog kunnen denken, goed, dan beperken we ons hier tot positieve waarden van h omdat we immers aan de rand van het domein van de functie zitten, en dan kunnen we in ieder geval nog de limiet bepalen van het differentiequotiënt als we h vanaf de positieve kant tot nul laten naderen. Dan bepaal je een zogeheten rechter limiet en daarmee ook een rechter afgeleide, maar dat gaat hier ook niet. Waarom niet?
Wel, als je nog even naar de grafiek kijkt, dan zie je dat deze steeds steiler gaat lopen naarmate we x dichter bij 0 kiezen. Dat is ook begrijpelijk, want voor f(x) = √x kunnen we ook schrijven f(x) = x1/2 en voor x > 0 is de afgeleide dan f'(x) = ½x−1/2 oftewel, we hebben
Nu zie je dat f'(x) inderdaad steeds groter wordt naarmate we x dichter bij 0 kiezen. Voor x = 0 krijgen we 1/0 maar dat heeft geen betekenis. De raaklijn aan de grafiek bij x = 0 loopt eigenlijk verticaal, maar een verticale lijn heeft geen richtingscoëfficiënt. Zo zie je dus dat het feit dat deze functie niet differentieerbaar is in het punt x = 0 nog een tweede reden heeft: een afgeleide in een punt is niets anders dan de richtingscoëfficiënt van de raaklijn aan de grafiek in dat punt, en als die raaklijn geen richtingscoëfficiënt heeft omdat die raaklijn verticaal loopt, dan is er voor dat punt dus ook geen afgeleide.
''Maar nu zie je het probleem: f(h) is niet gedefinieerd voor enige h < 0, en dus bestaat deze limiet niet. Het is niet noodzakelijk dat f(h) is gedefinieerd voor elke h als we f'(0) willen bepalen, maar f(h) moet in ieder geval wel zijn gedefinieerd voor elke h in een omgeving van 0 en dat is hier niet het geval.''quote:
[..]
Kijk nog eens naar de grafiek die je gaf bij je vorige post. Dit is de grafiek van de functie
f(x) = √x
Deze functie is alleen gedefinieerd voor x ≥ 0 oftewel op het interval [0, ∞), want √x is binnen R (de verzameling van alle reële getallen) niet gedefinieerd als x negatief is.
Bij x = 0 zitten we dus op de rand van het domein van deze functie, en je ziet ook dat de grafiek hier 'begint' (of 'stopt', zo je wil). Maar dit betekent dat deze functie niet differentieerbaar is voor x = 0. Waarom niet? Wel dat volgt om te beginnen uit de definitie van de afgeleide:
We moeten hier h naar nul kunnen laten gaan niet alleen vanaf de positieve kant, maar ook vanaf de negatieve kant, en het differentiequotiënt moet dan naderen tot dezelfde grenswaarde, en dat is dan de limiet van dit differentiequotiënt voor h → 0 oftewel de afgeleide. Als we de afgeleide voor x = 0 oftewel f'(0) willen bepalen dan hebben we volgens deze definitie
Maar nu zie je het probleem: f(h) is niet gedefinieerd voor enige h < 0, en dus bestaat deze limiet niet. Het is niet noodzakelijk dat f(h) is gedefinieerd voor elke h als we f'(0) willen bepalen, maar f(h) moet in ieder geval wel zijn gedefinieerd voor elke h in een omgeving van 0 en dat is hier niet het geval.
Nu zou je nog kunnen denken, goed, dan beperken we ons hier tot positieve waarden van h omdat we immers aan de rand van het domein van de functie zitten, en dan kunnen we in ieder geval nog de limiet bepalen van het differentiequotiënt als we h vanaf de positieve kant tot nul laten naderen. Dan bepaal je een zogeheten rechter limiet en daarmee ook een rechter afgeleide, maar dat gaat hier ook niet. Waarom niet?
Wel, als je nog even naar de grafiek kijkt, dan zie je dat deze steeds steiler gaat lopen naarmate we x dichter bij 0 kiezen. Dat is ook begrijpelijk, want voor f(x) = √x kunnen we ook schrijven f(x) = x1/2 en voor x > 0 is de afgeleide dan f'(x) = ½x−1/2 oftewel, we hebben
Nu zie je dat f'(x) inderdaad steeds groter wordt naarmate we x dichter bij 0 kiezen. Voor x = 0 krijgen we 1/0 maar dat heeft geen betekenis. De raaklijn aan de grafiek bij x = 0 loopt eigenlijk verticaal, maar een verticale lijn heeft geen richtingscoëfficiënt. Zo zie je dus dat het feit dat deze functie niet differentieerbaar is in het punt x = 0 nog een tweede reden heeft: een afgeleide in een punt is niets anders dan de richtingscoëfficiënt van de raaklijn aan de grafiek in dat punt, en als die raaklijn geen richtingscoëfficiënt heeft omdat die raaklijn verticaal loopt, dan is er voor dat punt dus ook geen afgeleide.
Dit begrijp ik niet. Die h is toch alleen maar het verschil tussen de afstand van punt 1 en punt 2 in het perspectief van de x-as? Dus als f'(0) is wat maakt het dan uit? Ik heb die h niet echt begrepen?
Ik weet wel dat de afgeleide van x1/2 = 1/2x-1/2 is. Maar dat komt doordat ik de regels uit mijn hoofd weet (constante, somregel, productregel en quotiëntregel).
P.S; als er in een x-punt de raaklijn f'(x) = 0 weergeeft, dan is het niet differentieerbaar in dat punt?
[ Bericht 1% gewijzigd door Super-B op 15-09-2014 16:31:15 ]
Als je de beschikking hebt over een scanner of een digitale camera, dan kun je in het vervolg beter een plaatje posten van de originele opgave uit je boek, want dit lijkt nergens op. Gebruik verder ook subscript voor indices en superscript voor exponenten, en controleer je formules op typo's voordat je iets post.quote:
'Show that f(x) = x^3 is strictly increasing. "
Nou allereerst moet ik de afgeleide bepalen en dat is 3x^2, maar vervolgens loop ik vast.. want er staat een hint waar ik een bepaalde sign moet gebruiken welke ik eerder niet heb gezien:
Hint: consider the sign of x(3/2) - (3/2) = (x2 - x1)(x2/1 + x1x2 + x 2/2)
Die deelstrepen behoren er niet want het is volgens mij geen breuk.
Het is kennelijk de bedoeling van de opgave om op elementaire wijze (dat is: zonder gebruik van differentiaalrekening) aan te tonen dat de functie f(x) = x3strict monotoon stijgend is op R. Dit betekent dat wanneer we twee willekeurige waarden x1 en x2 kiezen voor x met x2 > x1, dat dan gegarandeerd f(x2) > f(x1) is. Maar nu moeten we dit bewijzen. Hoe doen we dit?
Wel, x2 > x1 is equivalent met x2 − x1 > 0 en f(x2) > f(x1) is equivalent met f(x2) − f(x1) > 0. We moeten dus laten zien dat uit x2 − x1 > 0 volgt dat f(x2) − f(x1) > 0. We hebben
en met behulp van het merkwaardig product
kunnen we hiervoor schrijven
Nu is gegeven dat x2 > x1 en dus (x2 − x1) > 0 zodat we nu alleen nog hoeven te laten zien dat de tweede factor (x22 + x2x1 + x12) eveneens positief is, want dan is immers het product met (x2 − x1) en daarmee f(x2) − f(x1) ook positief.
Kijken we nu naar het merkwaardig product
dan zien we dat we kunnen schrijven
en dus hebben we evenzo
Aangezien de uitdrukking x22 + x2x1 + x12 gelijk is aan de halve som van de drie kwadraten x22, x12 en (x2 + x1)2, is deze uitdrukking dus steeds positief, behalve als x2 = x1 = 0 zou zijn, maar dat is niet het geval aangezien x2 > x1. En dus is inderdaad f(x2) - f(x1) = x23 − x13 = (x2 − x1)(x22 + x2x1 + x12) > 0 voor x2 > x1, QED.
Nee, die h kan ook negatief zijn, namelijk als het tweede punt (x+h, f(x+h)) links van het eerste punt (x, f(x)) ligt waarvoor we eigenlijk de richtingscoëfficiënt van de raaklijn willen bepalen door het tweede punt langs de grafiek naar het eerste punt te laten bewegen. Anders gezegd, we moeten h zowel vanaf de negatieve kant als vanaf de positieve kant naar nul kunnen laten gaan en het differentiequotiënt (f(x+h) − f(x))/h moet dan tot één en dezelfde grenswaarde naderen, ongeacht of we nu van links of van rechts komen. En aan deze voorwaarde is bij de functie f(x) = √x niet voldaan in het punt x = 0 omdat f(h) niet bestaat voor h < 0. De functie f(x) = √x is dus niet differentieerbaar in het punt x = 0, oftwel f'(0) bestaat hier niet.quote:
[..]
Maar nu zie je het probleem: f(h) is niet gedefinieerd voor enige h < 0, en dus bestaat deze limiet niet. Het is niet noodzakelijk dat f(h) is gedefinieerd voor elke h als we f'(0) willen bepalen, maar f(h) moet in ieder geval wel zijn gedefinieerd voor elke h in een omgeving van 0 en dat is hier niet het geval.
Dit begrijp ik niet. Die h is toch alleen maar het verschil tussen de afstand van punt 1 en punt 2 in het perspectief van de x-as? Dus als f'(0) is wat maakt het dan uit? Ik heb die h niet echt begrepen?
Nee, dat is onzin, f'(x) = 0 betekent dat de afgeleide f'(x) de waarde nul heeft of moet hebben voor een zekere waarde van x, en dat kan prima. Wat hier aan de hand is, is dat f'(x) gewoon geen waarde heeft en dus niet bestaat voor x = 0, oftewel f'(0) is niet gedefinieerd.quote:Ik weet wel dat de afgeleide van x1/2 = 1/2x-1/2 is. Maar dat komt doordat ik de regels uit mijn hoofd weet (constante, somregel, productregel en quotiëntregel).
P.S; als er in een x-punt de raaklijn f'(x) = 0 weergeeft, dan is het niet differentieerbaar in dat punt?
Omdat de wortel uit 0 niet gedefinieerd is?quote:
[..]
Nee, die h kan ook negatief zijn, namelijk als het tweede punt (x+h, f(x+h)) links van het eerste punt (x, f(x)) ligt waarvoor we eigenlijk de richtingscoëfficiënt van de raaklijn willen bepalen door het tweede punt langs de grafiek naar het eerste punt te laten bewegen. Anders gezegd, we moeten h zowel vanaf de negatieve kant als vanaf de positieve kant naar nul kunnen laten gaan en het differentiequotiënt (f(x+h) − f(x))/h moet dan tot één en dezelfde grenswaarde naderen, ongeacht of we nu van links of van rechts komen. En aan deze voorwaarde is bij de functie f(x) = √x niet voldaan in het punt x = 0 omdat f(h) niet bestaat voor h < 0. De functie f(x) = √x is dus niet differentieerbaar in het punt x = 0, oftwel f'(0) bestaat hier niet.
[..]
Nee, dat is onzin, f'(x) = 0 betekent dat de afgeleide f'(x) de waarde nul heeft of moet hebben voor een zekere waarde van x, en dat kan prima. Wat hier aan de hand is, is dat f'(x) gewoon geen waarde heeft en dus niet bestaat voor x = 0, oftewel f'(0) is niet gedefinieerd.
