[Bèta wiskunde] Huiswerk- en vragentopic.

quote:

Op donderdag 10 juli 2014 21:23 schreef netchip het volgende:

[..]

Riparius had die al gegeven.

Oh, nvm dan.

quote:

Op donderdag 10 juli 2014 14:28 schreef Novermars het volgende:

[..]

Was maar een grapje om mijn falen te maskeren!

Complexe machten van complexe getallen zijn lastiger dan je zo op het eerste gezicht zou denken. Voor a ∈ R⁺ en p ∈ R heb je a^p = exp(log(a^p)) = exp(p·log(a)) en je kunt je hierop baseren om voor a,p ∈ C, a ≠ 0 te definiëren

a^p := exp(p·log(a))

Nu is w = exp(z) in C periodiek met een periode 2πi, zodat omgekeerd log(w) = z niet eenduidig is, de (natuurlijke) logaritme van een complex getal w ≠ 0 is slechts bepaald tot op een geheel veelvoud van 2πi. De consequentie hiervan is dat conform bovenstaande definitie a^p in C eenduidig is dan en slechts dan als p ∈ Z. Als p ∈ Q\Z, zeg p = m/n met m en n geheel en onderling ondeelbaar en m ≠ 0, n > 1, dan heeft a^p precies n verschillende waarden in C. In alle overige gevallen heeft a^p oneindig veel waarden in C.

Dit betekent dat de notatie e^z in wezen ook niet eenduidig is binnen C, tenzij z ∈ Z. Maar in de praktijk beschouwt men e^z meestal als een alternatieve notatie voor exp(z) waardoor e^z dus wel eenduidig wordt voor elke z ∈ C terwijl a^z voor elke andere a ∈ C\{0} meerduidig blijft tenzij z ∈ Z.

De bekende rekenregels a^p·a^q = a^p+q en (a^p)^q = a^pq die gelden voor a ∈ R⁺ en p,q ∈ R gelden in het algemeen niet in C, ook niet als we ons beperken tot één (hoofd)waarde (principal branch) van de complexe logaritme. Als je hier geen rekening mee houdt en er evenmin rekening mee houdt dat de notatie e^z in het algemeen staat voor exp(z) dan kan dit aanleiding geven tot opmerkelijke paradoxen. Heel bekend in dit verband is de paradox van Clausen, gepubliceerd in 1827 (link naar originele publicatie). In een enigszins gemoderniseerde vorm luidt deze paradox als volgt.

Je weet dat voor elke k ∈ Z geldt e^2kπi = 1 en dus ook

e^1+2kπi = e

En dus zouden we moeten hebben:

(e^1+2kπi)^1+2kπi = e^1+2kπi

oftewel

e^-4k²π²∙e^1+4kπi = e

Nu is e^1+4kπi = e, en dus zou moeten gelden

e^-4k²π² = 1

maar dit is pertinent onjuist voor k ≠ 0.

[ Bericht 0% gewijzigd door Riparius op 11-07-2014 20:42:45 ]

quote:

Op donderdag 10 juli 2014 21:23 schreef netchip het volgende:

[..]

Riparius had die al gegeven.

Je maakt het veel te moeilijk voor jezelf. Denk eens aan een lineaire substitutie. Als je in de parametervoorstelling x = t, y = t² + 1 de t vervangt door, zeg, (t+1) of door pakweg (2t−3), dan heb je al een andere parametervoorstelling van precies dezelfde parabool.

quote:

Op donderdag 10 juli 2014 22:04 schreef Riparius het volgende:

[..]

Je maakt het veel te moeilijk voor jezelf. Denk eens aan een lineaire substitutie. Als je in de parametervoorstelling x = t, y = t² + 1 de t vervangt door, zeg, (t+1) of door pakweg (2t−3), dan heb je al een andere parametervoorstelling van precies dezelfde parabool.

Mag ik de kroon van te moeilijk denken?

quote:

Op donderdag 10 juli 2014 22:04 schreef Riparius het volgende:

[..]

Je maakt het veel te moeilijk voor jezelf. Denk eens aan een lineaire substitutie. Als je in de parametervoorstelling x = t, y = t² + 1 de t vervangt door, zeg, (t+1) of door pakweg (2t−3), dan heb je al een andere parametervoorstelling van precies dezelfde parabool.

Huh? (x+5)^2 is toch ook niet hetzelfde als x^2? Ik volg het niet helemaal meer...

quote:

Op donderdag 10 juli 2014 22:29 schreef Novermars het volgende:

[..]

Mag ik de kroon van te moeilijk denken?

Dat is een mooie inderdaad.

quote:

Op donderdag 10 juli 2014 22:31 schreef netchip het volgende:

[..]

Huh? (x+5)^2 is toch ook niet hetzelfde als x^2? Ik volg het niet helemaal meer...

Probeer het gewoon uit. Laten we t vervangen door (t+1), dan krijgen we

x = t+1
y = (t+1)² + 1

Nu geldt nog steeds y = x² + 1, dus dit is echt dezelfde parabool.

Vergelijk het maar met een soort meetlint dat je precies langs een curve drapeert. Het maakt niet uit of het meetlint nu een onderverdeling heeft in centimeters of in inches, de curve waar je het lint langs drapeert blijft precies hetzelfde, ook al hoort er bij elk punt op de curve nu een ander getalletje op het lint. En: als je het lint verschuift langs de curve dan veranderen de getalletjes van het lint bij elk punt op de curve ook, maar aan de curve zelf verandert niets.

quote:

Op donderdag 10 juli 2014 22:33 schreef Riparius het volgende:

[..]

Dat is een mooie inderdaad.

Duurde alleen veel te lang voordat ik er op kwam. Waren nooit mijn favoriete dingen, PV's

quote:

Op donderdag 10 juli 2014 22:43 schreef Novermars het volgende:

[..]

Duurde alleen veel te lang voordat ik er op kwam. Waren nooit mijn favoriete dingen, PV's

Waarom niet? Kun je leuke dingen mee doen. Oefeningetje (vooral voor Netchip):

Gegeven is een kromme met als parametervoorstelling

x = 2·sin t
y = sin 2t

Bepaal een cartesische vergelijking van deze kromme.

quote:

Op donderdag 10 juli 2014 22:40 schreef Riparius het volgende:

[..]

Probeer het gewoon uit. Laten we t vervangen door (t+1), dan krijgen we

x = t+1
y = (t+1)² + 1

Nu geldt nog steeds y = x² + 1, dus dit is echt dezelfde parabool.

Vergelijk het maar met een soort meetlint dat je precies langs een curve drapeert. Het maakt niet uit of het meetlint nu een onderverdeling heeft in centimeters of in inches, de curve waar je het lint langs drapeert blijft precies hetzelfde, ook al hoort er bij elk punt op de curve nu een ander getalletje op het lint. En: als je het lint verschuift langs de curve dan veranderen de getalletjes van het lint bij elk punt op de curve ook, maar aan de curve zelf verandert niets.

Oh, ik dacht dat alle punten ook 1:1 overeen moesten komen. De vorm blijft wel hetzelfde, inderdaad.

Ben nu bezig met je oefening. Ik heb nu x + y = sin(t) (2 + 2cos(t)). Hoe kan ik t 'elimineren'?

[ Bericht 2% gewijzigd door netchip op 10-07-2014 23:13:41 ]

Als f(x)-g(x)=s(x), klopt het dan om te zeggen dat S(x)= F(x)-G(x); waarbij S'(x) = s(x), F'(x)= f(x) en G'(x) = g(x)

[ Bericht 24% gewijzigd door GeorgeArArMartin op 12-07-2014 10:11:30 ]

quote:

Op zaterdag 12 juli 2014 10:05 schreef GeorgeArArMartin het volgende:
Als f(x)-g(x)=s(x), klopt het dan om te zeggen dat S(x)= F(x)-G(x); waarbij S'(x) = s(x), F'(x)= f(x) en G'(x) = g(x)

Niet honderd procent. Je mist een constant van integratie.

quote:

Op zaterdag 12 juli 2014 14:59 schreef Novermars het volgende:

[..]

Niet honderd procent. Je mist een constant van integratie.

Ik heb je een PM gestuurd. (Geen DM!)

quote:

Op zaterdag 12 juli 2014 14:59 schreef Novermars het volgende:

[..]

Niet honderd procent. Je mist een constant van integratie.

Ik ben ook verder gegaan met het probleem dat je me had gegeven.




[ Bericht 1% gewijzigd door netchip op 12-07-2014 15:29:07 ]

quote:

Op zaterdag 12 juli 2014 14:59 schreef Novermars het volgende:

[..]

Niet honderd procent. Je mist een constant van integratie.

Dus S(x) = F(x) - G(x) + C? Kun je me misschien verwijzen naar de naam van dit bewijs of de opzet ervan?

quote:

Op zaterdag 12 juli 2014 15:34 schreef GeorgeArArMartin het volgende:

[..]

Dus S(x) = F(x) - G(x) + C? Kun je me misschien verwijzen naar de naam van dit bewijs of de opzet ervan?

Een primitieve van een gegeven functie is altijd slechts bepaald tot op een constante. Dit is een eenvoudig gevolg van het feit dat de afgeleide van een constante functie identiek gelijk is aan nul.

Immers, zij F(x) een primitieve van f(x), dus F'(x) = f(x), dan is G(x) = F(x) + C met een willekeurige constante C eveneens een primitieve van f, want de afgeleide van G(x) is dan G'(x) = F'(x) + 0 = F'(x) = f(x). Je kunt dus in het algemeen ook niet spreken van de primitieve van een gegeven functie f(x) maar wel van een primitieve van die functie.

quote:

Op zaterdag 12 juli 2014 15:34 schreef GeorgeArArMartin het volgende:

[..]

Dus S(x) = F(x) - G(x) + C? Kun je me misschien verwijzen naar de naam van dit bewijs of de opzet ervan?

Fundamentele stelling van calculus met C_f + C_g = C
En wat Riparius zegt natuurlijk.

quote:

Op zaterdag 12 juli 2014 15:45 schreef Riparius het volgende:

[..]

Een primitieve van een gegeven functie is altijd slechts bepaald tot op een constante. Dit is een eenvoudig gevolg van het feit dat de afgeleide van een constante functie identiek gelijk is aan nul.

Immers, zij F(x) een primitieve van f(x), dus F'(x) = f(x), dan is G(x) = F(x) + C met een willekeurige constante C eveneens een primitieve van f, want de afgeleide van G(x) is dan G'(x) = F'(x) + 0 = F'(x) = f(x). Je kunt dus in het algemeen ook niet spreken van de primitieve van een gegeven functie f(x) maar wel van een primitieve van die functie.

Oké! Bedankt, zo had ik het nog niet bekeken.

quote:

Op zaterdag 12 juli 2014 15:50 schreef Novermars het volgende:

[..]

Fundamentele stelling van calculus met C_f + C_g = C
En wat Riparius zegt natuurlijk.

Ik snap even niet wat je met de lage streep bedoelt, hoort dat een minteken of subscript te zijn?

quote:

Op zaterdag 12 juli 2014 15:56 schreef GeorgeArArMartin het volgende:

[..]

Oké! Bedankt, zo had ik het nog niet bekeken.

[..]

Ik snap even niet wat je met de lage streep bedoelt, hoort dat een minteken of subscript te zijn?

Subscript.

Twee vraagjes:
Rudin 2.2: A complex number z is said to be algebraic if there integers a_0,...,a_n, not all zero, such that

Prove that the set of all algebraic numbers is countable.

Dan wordt er een hint gegeven die de vraag erg makkelijk maakt: Hint: For every positive integer N there are only finitely many equations with

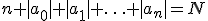
De vraag beantwoorden met de hint was zoals ik al zei vrij makkelijk, aangezien de vereniging van eindige verzameling hoogstens aftelbaar is en je concludeert omdat elk rationeel getal algebraïsch dat de verzameling van algebraïsche getallen aftelbaar is.
Maar wat is de gedachtegang achter deze hint? Met andere woorden, hoe was ik zelf bij deze hint uitgekomen?

En dan de tweede vraag: Construct a bounded set of real numbers with exactly three limit points.
Definitie van een limit point: A point p is a limit point of the set E (of a metric space X) if every neighbourhood of p contans a point q not equal to p such that q is in E.

Constructie vragen ben ik altijd erg slecht in :/

[ Bericht 0% gewijzigd door Novermars op 13-07-2014 13:52:17 ]

quote:

Op zaterdag 12 juli 2014 15:08 schreef netchip het volgende:

[..]

Ik ben ook verder gegaan met het probleem dat je me had gegeven.

Waarom dit zo is, ben ik nog niet helemaal over uit...

OHHHH, er staat nu 5⁵ⁱ = cos(5log(5)) + i*sin(5log(5))

Ik ben erover uit, geloof ik.

quote:

Op zondag 13 juli 2014 13:41 schreef netchip het volgende:

[..]

Waarom dit zo is, ben ik nog niet helemaal over uit...

OHHHH, er staat nu 5⁵ⁱ = cos(5log(5)) + i*sin(5log(5))

Ik ben erover uit, geloof ik.

Je hebt 5⁵ⁱ = exp(5i·log(5)), maar bedenk dat log(5) in C slechts bepaald is tot op een geheel veelvoud van 2πi, zodat exp(5i·log(5)) oneindig veel waarden heeft. Als je de reële natuurlijke logaritme van 5 noteert als ln(5), dan is

log(5) = ln(5) + 2kπi, k ∈ Z

en dus

5⁵ⁱ = exp(5i·log(5)) = exp(5i·(ln(5) + 2kπi)) = exp(−10kπ)·exp(5i·ln(5)) = exp(−10kπ)·(cos(5·ln(5)) + i·sin(5·ln(5))), k ∈ Z.

quote:

Op zondag 13 juli 2014 17:00 schreef Riparius het volgende:

[..]

Je hebt 5⁵ⁱ = exp(5i·log(5)), maar bedenk dat log(5) in C slechts bepaald is tot op een geheel veelvoud van 2πi, zodat exp(5i·log(5)) oneindig veel waarden heeft. Als je de reële natuurlijke logaritme van 5 noteert als ln(5), dan is

log(5) = ln(5) + 2kπi, k ∈ Z

en dus

5⁵ⁱ = exp(5i·log(5)) = exp(5i·(ln(5) + 2kπi)) = exp(−10kπ)·exp(5i·ln(5)) = exp(−10kπ)·(cos(5·ln(5)) + i·sin(5·ln(5))), k ∈ Z.

Dit zegt mij niet erg veel. Ik zal er een nachtje overslapen.

Leuk dat je er tijd insteekt om mij iets te leren over complexe getallen, Riparius. Ik merk dat ik nu nieuwe inzichten heb, jij vertelde dat een vermenigvuldiging met i een rotatie van 90 graden tegen de klok in betekent. Erg leuk (voor mij) om die kennis dan ook te gebruiken, omdat ik nu weet wat een vermigvuldiging met i inhoudt.

Het kwartje met de parametervoorstellingen is nu ook gevallen. Het principe is mij duidelijk. Het is eigenlijk een redelijk abstract principe als je gewend bent dat y een functie van x is.

quote:

Op maandag 14 juli 2014 23:16 schreef netchip het volgende:

[..]

Dit zegt mij niet erg veel. Ik zal er een nachtje overslapen.

Leuk dat je er tijd insteekt om mij iets te leren over complexe getallen, Riparius. Ik merk dat ik nu nieuwe inzichten heb, jij vertelde dat een vermenigvuldiging met i een rotatie van 90 graden tegen de klok in betekent. Erg leuk (voor mij) om die kennis dan ook te gebruiken, omdat ik nu weet wat een vermigvuldiging met i inhoudt.

Het kwartje met de parametervoorstellingen is nu ook gevallen. Het principe is mij duidelijk. Het is eigenlijk een redelijk abstract principe als je gewend bent dat y een functie van x is.

zodat exp(5i·log(5)) oneindig veel waarden heeft [in C]. Dat is het belangrijkste om te onthouden. De details zijn (nu) nog niet belangrijk voor je.

quote:

Op maandag 14 juli 2014 23:29 schreef Novermars het volgende:

[..]

zodat exp(5i·log(5)) oneindig veel waarden heeft [in C]. Dat is het belangrijkste om te onthouden. De details zijn (nu) nog niet belangrijk voor je.

Ik denk dat ik 'm snap. Die 2k*pi is mogelijk omdat de sinus en cosinus periodiek zijn met 2k*pi... En k zit in de collectie Z, die reikt van -oneindig naar +oneindig, right? Dan zijn er inderdaad oneindig veel waardes...

Of heb ik dit verkeerd beredeneerd?