SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Dat is de laatste vraag. Daar ben ik nog niet. Ik ga hem zo maken. Ik wist wel dat ik a en b moest berekenen, maar twijfelde. Ik laat het zo weten.quote:Op zondag 18 mei 2014 19:11 schreef Riparius het volgende:
[..]
Ja, dat is goed, als het de bedoeling is de nulpunten van de afgeleide te bepalen.
Ben je al verder gekomen met die vraag over buigpunten?
Een kleine vraag wat betreft maxima's en minima's. Welke is de meest veilige methode om te weten of het een maximum betreft of een minimum:
Kijkend naar het verloop van de afgeleide functie, dus stel x = 4 en dan kijken wat er gebeurt bij x =5 en x = 3 ?
Of tweede afgeleide bepalen en dan als die >0 is dan is het een (lokaal) minimum, is die 0< dan is het een (lokaal) maximum?
Kan je de vetgedrukte methode ook toepassen op de eerste afgeleide? Of moet je hiervoor echt de tweede afgeleide hebben?
Dude.quote:
[..]
Dat is de laatste vraag. Daar ben ik nog niet. Ik ga hem zo maken. Ik wist wel dat ik a en b moest berekenen, maar twijfelde. Ik laat het zo weten.
Een kleine vraag wat betreft maxima's en minima's. Welke is de meest veilige methode om te weten of het een maximum betreft of een minimum:
Kijkend naar het verloop van de afgeleide functie, dus stel x = 4 en dan kijken wat er gebeurt bij x =5 en x = 3 ?
Of tweede afgeleide bepalen en dan als die >0 is dan is het een (lokaal) minimum, is die 0< dan is het een (lokaal) maximum?
Kan je de vetgedrukte methode ook toepassen op de eerste afgeleide? Of moet je hiervoor echt de tweede afgeleide hebben?
Differentiëren in de monovariabele calculus is echt het simpelste wat er is.
?quote:Op zondag 18 mei 2014 19:18 schreef Amoeba het volgende:
[..]
Dude.
Differentiëren in de monovariabele calculus is echt het simpelste wat er is.
Bepaal gewoon de tweede afgeleide. Het is namelijk niet altijd veilig om maar een eenheid naar links of rechts op te schuiven en zodoende te kijken naar het functieverloop.quote:
Ik kan heus wel functies verzinnen waarbij jouw verhaaltje gewoon misgaat.
Nou ik heb er wel één waar het misgaat:quote:
[..]
Bepaal gewoon de tweede afgeleide. Het is namelijk niet altijd veilig om maar een eenheid naar links of rechts op te schuiven en zodoende te kijken naar het functieverloop.
Ik kan heus wel functies verzinnen waarbij jouw verhaaltje gewoon misgaat.
http://www.eur.nl/fileadm(...)au_2_versie_2014.pdf
opgave 3b.
Eerste afgeleide lukt, tweede afgeleide gaat compleet mis.. Evenals het oplossen.
Als je alle nulpunten hebt van de afgeleide dan kun je een tekenschema maken.quote:
[..]
Dat is de laatste vraag. Daar ben ik nog niet. Ik ga hem zo maken. Ik wist wel dat ik a en b moest berekenen, maar twijfelde. Ik laat het zo weten.
Een kleine vraag wat betreft maxima en minima. Welke is de meest veilige methode om te weten of het een maximum betreft of een minimum:
Kijkend naar het verloop van de afgeleide functie, dus stel x = 4 en dan kijken wat er gebeurt bij x =5 en x = 3 ?
Dat kan uiteraard ook. Houd er rekening mee dat dit een voldoende voorwaarde is voor een (lokaal) minimum resp. een (lokaal) maximum, maar geen noodzakelijke voorwaarde. De functie f(x) = x4 bijvoorbeeld heeft een (globaal, en dus ook lokaal) minimum bij x = 0, maar hier is f''(0) = 0 zodat je het criterium hier niet kunt gebruiken. Als de eerste afgeleide in een punt nul is, maar de tweede ook, dan kun je nog geen uitspraak doen. Een lokaal minimum, een lokaal maximum, of een buigpunt met een horizontale buigraaklijn zijn dan nog alle drie mogelijk.quote:Of tweede afgeleide bepalen en dan als die >0 is dan is het een (lokaal) minimum, is die 0< dan is het een (lokaal) maximum?
Je moet beide afgeleiden hebben. En dan heb jequote:Kan je de vetgedrukte methode ook toepassen op de eerste afgeleide? Of moet je hiervoor echt de tweede afgeleide hebben?
f'(x0) = 0 ∧ f''(x0) > 0 ⇒ f heeft een lokaal minimum bij x = x0
f'(x0) = 0 ∧ f''(x0) < 0 ⇒ f heeft een lokaal maximum bij x = x0
Laat eens zien wat je gedaan hebt om de tweede afgeleide te bepalen.quote:
[..]
Nou ik heb er wel één waar het misgaat:
http://www.eur.nl/fileadm(...)au_2_versie_2014.pdf
opgave 3b.
Eerste afgeleide lukt, tweede afgeleide gaat compleet mis.. Evenals het oplossen.
De eerste is:quote:
[..]
Laat eens zien wat je gedaan hebt om de tweede afgeleide te bepalen.
(-2x + 2)e-x² + 2x
Vervolgens pas ik de productregel toe:
-2(-2x + 2) e-x² + 2x -2x + 2(-2x+2)e-x² + 2x
Werk het nu eens verder uit.quote:
[..]
De eerste is:
(-2x + 2)e-x² + 2x
Vervolgens pas ik de productregel toe:
-2 e-x² + 2x + (-2x + 2)(-2x + 2)e-x² + 2x
[ Bericht 0% gewijzigd door Riparius op 18-05-2014 19:47:20 ]
-2(-2x + 2) e-x² + 2x -2x + 2(-2x+2)e-x² + 2xquote:
-2(-2x + 2) e-x² + 2x + (-2x + 2) (-2x+2)e-x² + 2x
-2(-2x + 2) e-x² + 2x + (4x² - 8x +4)e-x² + 2x
Kijk nu eens goed wat je hebt. De eerste factor van je product is (−2x + 2) en de tweede is e−x²+2x.quote:
Productregel:
(uv)' = u'v + uv'
Dan kom ik nu uit op:quote:
[..]
Kijk nu eens goed wat je hebt. De eerste factor van je product is (−2x + 2) en de tweede is e−x²+2x.
Productregel:
(uv)' = u'v + uv'
-2xe-x² + 2x + (4x² - 8x +4)e-x² + 2x
De afgeleide van (−2x + 2) is −2. Nu verder uitwerken.quote:
[..]
Dan kom ik nu uit op:
-2e-x² + 2x + (4x² - 8x + 4)e-x² + 2x
Ik zit vast..quote:
[..]
De afgeleide van (−2x + 2) is −2. Nu verder uitwerken.
Nee hoor. Je bent er bijna. Er zat alleen een factor x teveel in je eerste term. Ik vermoed dat je daar een x hebt gebruikt om vermenigvuldiging aan te geven, maar dat moet je beslist niet doen.quote:
-2e-x² + 2x + 2(2x² - 4x +2)e-x² + 2xquote:
[..]
Nee hoor. Je bent er bijna. Er zat alleen een factor x teveel in je eerste term. Ik vermoed dat je daar een x hebt gebruikt om vermenigvuldiging aan te geven, maar dat moet je beslist niet doen.
Nu zit ik echt vast.
Ik zeg het niet voor niets héquote:
[..]
Ja klopt, maar die -2 staat in de weg..
Kijk eens of je dat kan toepassen.
Je had nog even niet die factor 2 buiten haakjes moeten halen in de tweede term, maar eerst de termen samennemen.quote:
[..]
-2e-x² + 2x + 2(2x² - 4x +2)e-x² + 2x
Nu zit ik echt vast.
We hadden
-2e-x² + 2x + (4x² - 8x + 4)e-x² + 2x
Nu zie je dat beide termen een facor e-x² + 2x gemeen hebben en die kunnen we dus buiten haakjes halen. Dan krijgen we
(-2 + 4x² - 8x + 4)e-x² + 2x
en dus
(4x² - 8x + 2)e-x² + 2x
En nu pas die factor 2 van de kwadratische veelterm buiten haakjes halen en je hebt
2(2x² - 4x + 1)e-x² + 2x
Zie je?
Nu de nulpunten bepalen van deze tweede afgeleide en dan een tekenschema maken van deze tweede afgeleide.
Tering.. Goed zeg.. Ik sloeg die tussenstap inderdaad over qua gedachte...quote:
[..]
Je had nog even niet die factor 2 buiten haakjes moeten halen in de tweede term, maar eerst de termen samennemen.
We hadden
-2e-x² + 2x + (4x² - 8x + 4)e-x² + 2x
Nu zie je dat beide termen een facor e-x² + 2x gemeen hebben en die kunnen we dus buiten haakjes halen. Dan krijgen we
(-2 + 4x² - 8x + 4)e-x² + 2x
en dus
(4x² - 8x + 2)e-x² + 2x
En nu pas die factor 2 van de kwadratische veelterm buiten haakjes halen en je hebt
2(2x² - 4x + 1)e-x² + 2x
Zie je?
Nu de nulpunten bepalen van deze tweede afgeleide en dan een tekenschema maken van deze tweede afgeleide.
Ik weet niet zo goed hoe ik de nulpunten uit zo'n ingewikkelde functie moet bepalen.. Ben niet zo goed met het getal e.
Ik zou zeggen om de nulpunten binnen de haakjes te vinden.
Als de toets morgen in de buurt zit van het niveau van de oefentoets heb ik er nog wel vertrouwen in.
Zeker.. Minimaal een 6 moet lukken. Eerste keer was bij jou een 6,2 toch? Hoeveel heb je bij de tweede keer gescoord?quote:Op zondag 18 mei 2014 20:14 schreef nodig het volgende:
Als de toets morgen in de buurt zit van het niveau van de oefentoets heb ik er nog wel vertrouwen in.
Heb maar een paar opgaven gemaakt. Die had ik dit keer wel goed. Maarja, wat wil je als je een toets voor een 2e keer gaat makenquote:
[..]
Zeker.. Minimaal een 6 moet lukken. Eerste keer was bij jou een 6,2 toch? Hoeveel heb je bij de tweede keer gescoord?
Zie antwoordmodel. Daar staat hoe je hem kan herschrijven.quote:
Hoe moet ik opgave 4c maken?
http://www.eur.nl/fileadm(...)au_2_versie_2014.pdf
De herschrijving begrijp ik dus niet.quote:
[..]
Zie antwoordmodel. Daar staat hoe je hem kan herschrijven.
Al iets geprobeerd?quote:
Hoe moet ik opgave 4c maken?
http://www.eur.nl/fileadm(...)au_2_versie_2014.pdf
Hmm... Nu 4 keer opnieuw uitgewerkt - of iets in die richting.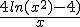 
daar de afgeleide van. Ik kom dus de hele tijd uit op: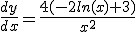 
Wat doe ik fout? Ik gebruik de productregel.
Wat doe ik fout? Ik gebruik de productregel.
Hij ziet er wat ingewikkeld uit, maar die e-macht heeft de prettige eigenschap dat ie altijd positief is. De factor met de e-macht kan dus nooit nul zijn, en we hoeven dus inderdaad alleen te kijken naar de kwadratische veelterm tussen de haakjes. Dan krijgen we dus als voorwaarde voor de nulpuntenquote:
[..]
Tering.. Goed zeg.. Ik sloeg die tussenstap inderdaad over qua gedachte...
Ik weet niet zo goed hoe ik de nulpunten uit zo'n ingewikkelde functie moet bepalen.. Ben niet zo goed met het getal e.
Ik zou zeggen om de nulpunten binnen de haakjes te vinden.
2x² − 4x + 1 = 0
ik ga deze even voor je doen via kwaadraatafsplitsing, dat geeft minder kans op fouten dan de abc-formule en dan zie je dat ook eens. Eerst delen we even beide leden door 2, dat geeft
x² − 2x + ½ = 0
Nu weten we dat (x − 1)2 = x² − 2x + 1 en dat is bijna wat er links staat. We komen nog een ½ te kort, maar dat kunnen we oplossen door links en rechts ½ op te tellen. Dan hebben we
x² − 2x + 1 = ½
en dus
(x − 1)2 = ½
en dus
x − 1 = √½ ∨ x − 1 = −√½
Nu is √½ = ½√2, dus
x − 1 = ½√2 ∨ x − 1 = −½√2
en dus
x = 1 + ½√2 ∨ x = 1 − ½√2
Hoe ziet nu het tekenschema van de tweede afgeleide eruit?
[ Bericht 0% gewijzigd door Riparius op 18-05-2014 20:58:16 ]
Hoe bedoel je tekenschema? De x-waarden van de tweede afgeleiden zijn in ieder geval de buigpunten.quote:
[..]
Hij ziet er wat ingewikkeld uit, maar die e-macht heeft de prettige eigenschap dat ie altijd positief is. De factor met de e-macht kan dus nooit nul zijn, en we hoeven dus inderdaad alleen te kijken naar de kwadratische veelterm tussen de haakjes. Dan krijgen we dus als voorwaarde voor de nulpunten
2x² − 4x + 1 = 0
ik ga deze even voor je doen via kwaadratafsplitsing, dat geeft minder kans op fouten dan de abc-formule en dan zie je dat ook eens. Eerst delen we even beide leden door 2, dat geeft
x² − 2x + ½ = 0
Nu weten we dat (x − 1)2 = x² − 2x + 1 en dat is bijna wat er links staat. We komen nog een ½ te kort, maar dat kunnen we oplossen door links en rechts ½ op te tellen. Dan hebben we
x² − 2x + 1 = ½
en dus
(x − 1)2 = ½
en dus
x − 1 = √½ ∨ x − 1 = −√½
Nu is √½ = ½√2, dus
x − 1 = ½√2 ∨ x − 1 = −½√2
en dus
x = 1 + ½√2 ∨ x = 1 − ½√2
Hoe ziet nu het tekenschema van de tweede afgeleide eruit?
Gewoon de rekenregels voor machten gebruiken. Je hebt (3x)2 = 3x·2 = 32·x = (32)x = 9xquote:
en ook
1/93x+4 = 9−(3x+4) = 9−3x−4
En dus wordt de vergelijking
9x = 9−3x−4
en dat geeft
x = −3x−4
4x = −4
x = −1
Nee, dat is niet zo. Je hebt een buigpunt bij x = x0 als f''(x0) = 0 en als de tweede afgeleide hier ook van teken wisselt. Daarom moet je een tekenschema maken. En het zijn geen x-waarden maar de nulpunten van de tweede afgeleide die we nu hebben gevonden.quote:
[..]
Hoe bedoel je tekenschema? De x-waarden van de tweede afgeleiden zijn in ieder geval de buigpunten.
Waarom wordt er een min genomen die wordt vermenigvuldigd? Ik dacht dat er een -1 kwam en dus werd [b]9&minus[/b];3x−5quote:
[..]
Gewoon de rekenregels voor machten gebruiken. Je hebt (3x)2 = 3x·2 = 32·x = (32)x = 9x
en ook
1/93x+4 = 9−(3x+4) = 9−3x−4
En dus wordt de vergelijking
9x = 9−3x−4
en dat geeft
x = −3x−4
4x = −4
x = −1
En waardoor verandert 9x = [b]9&minus[/b];3x−4 in x = −3x−4 ?
Nee.. Ik snap de bedoeling maar heb het toch onderschat dat a en b berekenen. Makkelijker gezegd dan gedaan..quote:
[..]
Ja, dat is goed, als het de bedoeling is de nulpunten van de afgeleide te bepalen.
Ben je al verder gekomen met die vraag over buigpunten?
Eerste en tweede afgeleiden bepalen is geen probleem. Maar bij het bepalen van de afgeleiden valt a en b weg.. Waardoor ik mij dus afvraag hoe ik deze dan moet berekenen..
Je kent toch wel de regelquote:
[..]
Waarom wordt er een min genomen die wordt vermenigvuldigd?
1/ap = a−p
?
Ja moet wel.. Anders heb ik een groot probleem morgen. Ohja ik verkeek me op die 1 in de teller.quote:
Maar hoezo valt de exponent weg en wordt het gewoon getallen die -3x - 4 ?
Kennelijk toch wel een probleem voor jou. Als je zowel a als b bent kwijtgeraakt, dan heb je het fout gedaan bij het differentiëren. Laat eens zien wat je hebt gedaan om de eerste en de tweede afgeleide te bepalen.quote:
[..]
Nee.. Ik snap de bedoeling maar heb het toch onderschat dat a en b berekenen. Makkelijker gezegd dan gedaan..
Eerste en tweede afgeleiden bepalen is geen probleem. Maar bij het bepalen van de afgeleiden valt a en b weg.. Waardoor ik mij dus afvraag hoe ik deze dan moet berekenen..
Er valt niets weg, maar het is toch heel eenvoudig: als twee machten van hetzelfde grondtal aan elkaar gelijk zijn, dan moeten de exponenten wel aan elkaar gelijk zijn. Dat is wat ik hier gebruik.quote:
[..]
Ja moet wel.. Anders heb ik een groot probleem morgen. Ohja ik verkeek me op die 1 in de teller.
Maar hoezo valt de exponent weg en wordt het gewoon getallen die -3x - 4 ?
ax^4 - 8x³ + bquote:
[..]
Kennelijk toch wel een probleem voor jou. Als je zowel a als b bent kwijtgeraakt, dan heb je het fout gedaan bij het differentiëren. Laat eens zien wat je hebt gedaan om de eerste en de tweede afgeleide te bepalen.
f(x)' = 4x - 24x
Want a en b zijn een constante.. en die vallen weg. Dus dan alleen de afgeleide van x^4 - 8x³ en dat is dan 4x - 24x
Bedankt voor je informatie...quote:
[..]
ax^4 - 8x³ + b
f(x)' 4x - 24x
Want a en b zijn een constante..
