SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Veronderstel je nu dat iets delen door 0 gelijkstaat aan 0?quote:Op maandag 5 mei 2014 13:34 schreef Super-B het volgende:
Snappen jullie dit? Ik snap het niet echt.. wat maakt het uit als het antwoord op 0 komt bij asymptoten? Dan is het coördinaat van y gewoon 0 toch?
Ohhh ik zie het al.. kan niet.quote:
[..]
Veronderstel je nu dat iets delen door 0 gelijkstaat aan 0?
Ik raakte even in de war met het berekenen van desnijpunten met beide coördinaatassen.
Hoe kun je de snijpunten met de coördinaatassen bepalen van 3 / (2x-4) ? Wat ik weet is dat x = 0 of y = 0. 
Bij de y-as is het mij gelukt door x = 0 in te vullen:quote:
Vul beiden eens in om mee te beginnen.
3 / (2*0 - 4) = -1
Dus de y-coördinaat is -3/4, maar om de x-coördinaat te weten, moet ik f(0) hebben...
Dus... 3 / (2x-4) = 0 , maar ik weet niet hoe ik verder moet...
Hmm wat je voor je bewerkte post zei, klopt niet. Dan zou ik 2x - 4 = 0 moeten pakken, maar dan krijg ik x = 2 eruit en dat is niet de bedoeling.quote:
Er zijn geen snijpunten met de x-as omdat de teller van de breuk 3 / (2x-4) nooit 0 is.quote:
[..]
Bij de y-as is het mij gelukt door x = 0 in te vullen:
3 / (2*0 - 4) = -1
Dus de y-coördinaat is -3/4, maar om de x-coördinaat te weten, moet ik f(0) hebben...
Dus... 3 / (2x-4) = 0 , maar ik weet niet hoe ik verder moet...
Kap eens met f(x) = 0 oplossen door elkaar gebruiken met f(0) zeggen.
Dus de teller zegt iets over de x-as en de noemer over de y-as?quote:
[..]
Er zijn geen snijpunten met de x-as omdat de teller van de breuk 3 / (2x-4) nooit 0 is.
Kap eens met f(x) = 0 oplossen door elkaar gebruiken met f(0) zeggen.
Oh ja hahaha excuus... f(0) staat voor dat de x-waarden vervangen wordt door 0... foutje..
Ik heb er vrij weinig van begrepen hoe ik alle snijpunten met de coördinaatassen moet berekenen, met een normale functie weet ik het wel (y=0 en x=0), maar bij een gebroken functie heb ik geen flauw idee..
Je wilt weten voor welke x geldt f(x) = 0 en je kreeg dat moet gelden 3 / (2x-4) = 0.
Vermenigvuldig beide kanten met (2x-4) en je ziet dat er geen oplossing is.
In het algemeen
a/b = 0 dan en slechts dan als a = 0
Want vermenigvuldigen met b aan beide kanten geeft dat moet gelden a = 0.
Vermenigvuldig beide kanten met (2x-4) en je ziet dat er geen oplossing is.
In het algemeen
a/b = 0 dan en slechts dan als a = 0
Want vermenigvuldigen met b aan beide kanten geeft dat moet gelden a = 0.
Ik heb al een trucje uitgeprobeerd en het lijkt te werken:quote:
Je wilt weten voor welke x geldt f(x) = 0 en je kreeg dat moet gelden 3 / (2x-4) = 0.
Vermenigvuldig beide kanten met (2x-4) en je ziet dat er geen oplossing is.
In het algemeen
a/b = 0 dan en slechts dan als a = 0
Want vermenigvuldigen met b aan beide kanten geeft dat moet gelden a = 0.
3 / (2x - 4)
y-coördinaat is te vinden bij x = 0, dus de uitkomst is dat y-coördinaat = -3/4
-3/4 invullen in de formule:
-3/4 = 3 / (2x-4)
3 = -3/4 (2x - 4 )
3 = -1,5x + 3
0 = -1,5x
0 / -1,5 = 0 dus x = 0
(0, -3/4)
Wat probeer je hier te doen?
Dat y = -3/4 het snijpunt met de y-as is wist je al door x = 0 in te vullen.
Dan hoef je niet weer y = - 3/4 in te vullen in de formule/
Dat y = -3/4 het snijpunt met de y-as is wist je al door x = 0 in te vullen.
Dan hoef je niet weer y = - 3/4 in te vullen in de formule/
Oh voor de zekerheid,quote:
Wat probeer je hier te doen?
Dat y = -3/4 het snijpunt met de y-as is wist je al door x = 0 in te vullen.
Dan hoef je niet weer y = - 3/4 in te vullen in de formule/
bij bijvoorbeeld het volgende formule doe ik het als volgt:
(x + 2) / (x - 2 )
y-coördinaat bij x = 0 is 2 / -2 = -1 (0 , -1)
x-coördinaat bij y = 0 is 0 = (x + 2) / (x - 2 )
(x+2) = 0(x-2)
x+2 = 0
x = - 2
dus de snijpunten zijn: (0 , -1) en ( -2, 0 )
Hoe weet ik of er überhaupt al een tweede snijpunt is?:
3 / (2x - 4)
zoals de net met x = 0 resulteert het tot (0, -3/4) als eerste snijpunt.
Eventueel tweede snijpunt:
0 = 3 / (2x - 4)
3 = 0(2x - 4)
3 = 0 --> dus geen tweede snijpunt.
Dit is de methode die ik gebruik i.i.g.
3 / (2x - 4)
zoals de net met x = 0 resulteert het tot (0, -3/4) als eerste snijpunt.
Eventueel tweede snijpunt:
0 = 3 / (2x - 4)
3 = 0(2x - 4)
3 = 0 --> dus geen tweede snijpunt.
Dit is de methode die ik gebruik i.i.g.
Als f(x) = 0 geen oplossing heeft dan is er geen snijpunt met de x-as.
En bijvoorbeeld f(x) = 1/x heeft geen snijpunt met de y-as.
En bijvoorbeeld f(x) = 1/x heeft geen snijpunt met de y-as.
''Voor welke reële getallen x geldt dat -1 < f(x) < 1 ''
''Bij de formule 1 / (x+3)''
Ik weet wat ik moet doen en ik krijg dan ook -4 en -2, maar ik weet niet naar welke kanten de groter/kleiner dan tekens op moeten. Weet iemand hoe ik dat kan zien ?
''Bij de formule 1 / (x+3)''
Ik weet wat ik moet doen en ik krijg dan ook -4 en -2, maar ik weet niet naar welke kanten de groter/kleiner dan tekens op moeten.
Weet iemand hoe ik dat kan zien ?
Jep klopt.quote:Op maandag 5 mei 2014 15:07 schreef Anoonumos het volgende:
Als f(x) = 0 geen oplossing heeft dan is er geen snijpunt met de x-as.
En bijvoorbeeld f(x) = 1/x heeft geen snijpunt met de y-as.
Misschien helpt deze post van Ripariusquote:
''Voor welke reële getallen x geldt dat -1 < f(x) < 1 ''
''Bij de formule 1 / (x+3)''
Ik weet wat ik moet doen en ik krijg dan ook -4 en -2, maar ik weet niet naar welke kanten de groter/kleiner dan tekens op moeten.
SES / [Bèta wiskunde] Huiswerk- en vragentopic
En/of de posts ervoor en erna
Je moet in ieder geval -1 < f(x) en f(x) < 1 apart bekijken.
Ik ben even weg, succes.
Oké bedankt!quote:
[..]
Misschien helpt deze post van Riparius
SES / [Bèta wiskunde] Huiswerk- en vragentopic
En/of de posts ervoor en erna
Je moet iig -1 < f(x) en f(x) < 1 apart bekijken.
Ik ben even weg, succes.
Weet iemand hoe ik 6x² - 8x - 8 gemakkelijk kan oplossen? Ik kan namelijk alles delen door 6, maar dan kom ik niet lekker uit... allemaal breuken..
Oplossen? Je geeft enkel een formule.. iets duidelijker graag.quote:
Weet iemand hoe ik 6x² - 8x - 8 gemakkelijk kan oplossen? Ik kan namelijk alles delen door 6, maar dan kom ik niet lekker uit... allemaal breuken..
Jep.. oplossen om zo te weten wat x kan zijn. Het kan d.m.v. abc formule en het antwoord een breuk laten maken via mijn Casio rekenmachine, maar ik ben benieuwd naar een makkelijke methode zonder de abc formule.quote:Op maandag 5 mei 2014 15:43 schreef jordyqwerty het volgende:
[..]
Oplossen? Je geeft enkel een formule..
Dus volgens jou is het domein van de functie f(x) = 6x² - 8x - 8 beperkt?quote:
[..]
Jep.. oplossen om zo te weten wat x kan zijn.
Hoe bedoel je beperkt?quote:
[..]
Dus volgens jou is het domein van de functie f(x) = 6x² - 8x - 8 beperkt?
Dat zijn de wortels van de formule. De x-coördinaten van de snijpunten met de y-as. Niet 'wat x kan zijn', want het domein van x is R. Er geldt dus f(x) = 0, 'f(x) oplossen' is ietwat te algemeen, je kan namelijk ook toppen bepalen e.d.quote:
[..]
Jep.. oplossen om zo te weten wat x kan zijn. Het kan d.m.v. abc formule en het antwoord een breuk laten maken via mijn Casio rekenmachine, maar ik ben benieuwd naar een makkelijke methode zonder de abc formule.
x-coördinaten van de snijpunten met y-as bepalen bedoel ik dan.quote:
[..]
Dat zijn de wortels van de formule. De x-coördinaten van de snijpunten met de y-as. Niet 'wat x kan zijn', want het domein van x is R. Er geldt dus f(x) = 0, 'f(x) oplossen' is ietwat te algemeen, je kan namelijk ook toppen bepalen e.d.
Maar volgens mij is dat meestal zo, althans dat doe je meestal met de abc-formule en het oplossen van zowel eerstegraads als tweedegraadsfuncties.
quote:
[..]
Ik heb al een trucje uitgeprobeerd en het lijkt te werken:
3 / (2x - 4)
y-coördinaat is te vinden bij x = 0, dus de uitkomst is dat y-coördinaat = -3/4
-3/4 invullen in de formule:
-3/4 = 3 / (2x-4)
3 = -3/4 (2x - 4 )
3 = -1,5x + 3
0 = -1,5x
0 / -1,5 = 0 dus x = 0
(0, -3/4)
!
Op
Juist!quote:Op maandag 5 mei 2014 16:18 schreef nodig het volgende:
[..]
Hij controleert gewoon of hij het goed heeft gedaan.
Je stelt eerstquote:
x = y
En gaat y voor x = 0 uitrekenen.
Vervolgens ga je die y waarde opnieuw substitueren, logischerwijs gaat hieruit x = 0 volgen.
Inderdaad.. Maar ik kwam er dus later achter.quote:
[..]
Je stelt eerst
x = y
En gaat y voor x = 0 uitrekenen.
Vervolgens ga je die y waarde opnieuw substitueren, logischerwijs gaat hieruit x = 0 volgen.
Ben jij al voorbij de absolute-waardefunctie geweest qua stof?
Hoe zou ik beginnen met het uitrekenen van deze reeks?
Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caparet
Jep. Ik ben nu bij differentiëren.quote:
[..]
Inderdaad.. Maar ik kwam er dus later achter.
Ben jij al voorbij de absolute-waardefunctie geweest qua stof?
Heb jij nog andere leerplekken geraadpleegd? Want het lijkt mij dat die van het boek te weinig uitleg erover geeft...quote:
Ik heb namelijk geen flauw idee hoe ik de vergelijking x^4 < x³ kan oplossen, naast het feit dat ik het vereenvoudigd op kan schrijven als x² < x.
Vereenvoudig nog eens een stapje verder.quote:
[..]
Heb jij nog andere leerplekken geraadpleegd? Want het lijkt mij dat die van het boek te weinig uitleg erover geeft...
Ik heb namelijk geen flauw idee hoe ik de vergelijking x^4 < x³ kan oplossen, naast het feit dat ik het vereenvoudigd op kan schrijven als x² < x.
Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caparet
Ja. khanacademy.org en wiskundeacademie op youtube.quote:
[..]
Heb jij nog andere leerplekken geraadpleegd? Want het lijkt mij dat die van het boek te weinig uitleg erover geeft...
Ik heb namelijk geen flauw idee hoe ik de vergelijking x^4 < x³ kan oplossen, naast het feit dat ik het vereenvoudigd op kan schrijven als x² < x.
Voor absolute waarde-functie heb ik trouwens khanacademy gebruikt.
x ( x - 1 ) < 0quote:
[..]
Vereenvoudig nog eens een stapje verder.
x = 0 of x = 1
En dan even waarden onder/boven 0 en onder/boven 1 invullen om te kijken wanneer x^3 groter is dan x^3 en dan resulteert dat toch 0 < x < 1
Wacht, niets zeggen, ik zie ineens iets.quote:Op maandag 5 mei 2014 16:20 schreef Diacetylmorfine het volgende:
Hoe zou ik beginnen met het uitrekenen van deze reeks?
[ afbeelding ]
Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caparet
De baan van P is gegeven door de parameter voorstelling
x = -1 + 2 cos(t)
y = 3 + 2sin(t)
met t op [0,3/2π]
De baan van P snijdt de lijn l: y = x + 4 in de punten B en C. Bereken exact de coördinaten van B en C.
Nu kan ik er zelf an sich wel uitkomen
x = -1 + 2 cos(t)
y = 3 + 2sin(t)
met t op [0,3/2π]
De baan van P snijdt de lijn l: y = x + 4 in de punten B en C. Bereken exact de coördinaten van B en C.
Nu kan ik er zelf an sich wel uitkomen
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt., maar in de uitwerkingen wordt de richtingscoëfficient van l genomen en vanuit daar direct gesteld dat bij B 1/4π hoort en bij C 5/4π. Hoe?
[ Bericht 13% gewijzigd door jordyqwerty op 05-05-2014 16:40:31 ]
Nee, met integreren en vergelijken met de meetkundige reeks kom ik ook niet verder.quote:
[..]
Wacht, niets zeggen, ik zie ineens iets.
Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caparet
Ik zou eerstquote:Op maandag 5 mei 2014 16:46 schreef Diacetylmorfine het volgende:
[..]
Nee, met integreren en vergelijken met de meetkundige reeks kom ik ook niet verder.
Dan haakjes uitwerken en je som schrijven als 4 afzonderlijke sommen
Met a en b ... de coefficienten van het polynoom in k na de substitutie.
De eerste som moet je weten.
En de formules voor
x^4 > | x |³
Ik kom uit op x = 0 , x (< of > ) 1 en x (< of > ) -1
Ergens een aantal pagina's terug staat er een post van Riparius m.b.t. de getallenrijen, maar ik vul gewoon getallen in om zodoende erachter te komen welke > is en welke <.
Echter kom ik er niet uit, dus keek ik naar het antwoordenmodel en er stond x = 0 en x < -1 en x > 1..
Maar als ik waarden invul klopt er niks van.. bij bijvoorbeeld -0,5 blijft x^4 groter dan x³...
Ik kom uit op x = 0 , x (< of > ) 1 en x (< of > ) -1
Ergens een aantal pagina's terug staat er een post van Riparius m.b.t. de getallenrijen, maar ik vul gewoon getallen in om zodoende erachter te komen welke > is en welke <.
Echter kom ik er niet uit, dus keek ik naar het antwoordenmodel en er stond x = 0 en x < -1 en x > 1..
Maar als ik waarden invul klopt er niks van.. bij bijvoorbeeld -0,5 blijft x^4 groter dan x³...
Het is dan ook |x|³ en niet x³.quote:
x^4 > | x |³
Maar als ik waarden invul klopt er niks van.. bij bijvoorbeeld -0,5 blijft x^4 groter dan x³...
Ja, daar was ik al in een andere volgorde aan begonnen, maar daar kwam niet veel uit. Althans, dat meende ik; vandaar ook mijn vorige post. Maar ik lees net nog eens mijn berekening door, omdat het toch zou moeten werken, en ik merk een fout op. Juiste berekening volgt zodadelijk.quote:
[..]
Ik zou eerstsubstitueren zodat je som bij 0 begint.
Dan haakjes uitwerken en je som schrijven als 4 afzonderlijke sommen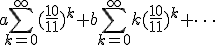
Met a en b ... de coefficienten van het polynoom in k na de substitutie.
De eerste som moet je weten.
En de formules voorkan je afleiden door de vorige uitdrukking af te leiden, geloof ik.
Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caparet
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |