SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Kan iemand hier de juiste berekening van geven? Ik kom wel op de juiste antwoorden maar volgens mij niet op de juiste manier..
Hoe kun je aan de oplossing zelf zien dat de oplossing is ''alle p'' ?quote:Op zondag 4 mei 2014 22:15 schreef Anoonumos het volgende:
f (x) = ax²+ bx + c
D = b²- 4ac
Nu
f (x) = x²+ 2px - 1
Dus a = 1 , b = 2p , c = -1
D = (2p)² - 4 * 1 * (-1) = 4p² + 4 = 4(p²+1)
Er zijn twee verschillende snijpunten met de x-as als D > 0.
Voor elke p geldt dat p² ≥ 0.
En dus geldt voor elke p dat p² + 1 > 0
Dus D > 0 voor alle p.
Dus voor elke p zijn er twee verschillende snijpunten met de x-as.
Aan 4(p² + 1) kan ik dat niet zo direct zien.
Waarom? Er staat geen x bij. p kun je in dit geval zien als niets meer dan een willekeurig getal.quote:
Voor elke p geldt toch dat het resulterende getal groter is dan 0?quote:
[..]
Hoe kun je aan de oplossing zelf zien dat de oplossing is ''alle p'' ?
Aan 4(p² + 1) kan ik dat niet zo direct zien.
Een kwadraat kan niet negatief zijn. Dus is p2 altijd groter dan of gelijk aan nul. Maar dan is p2 + 1 dus altijd tenminste 1 en 4(p2 + 1) dus altijd tenminste 4. De discriminant is dus altijd positief, en de corresponderende kwadratische vergelijking heeft dus altijd twee (verschillende) oplossingen.quote:
[..]
Hoe kun je aan de oplossing zelf zien dat de oplossing is ''alle p'' ?
Aan 4(p² + 1) kan ik dat niet zo direct zien.
Ja de merkwaardige producten ben ik eerder tegengekomen:quote:
[..]
Nee. Zorg dat je je merkwaardige producten kent. Zie ook hier.
4p^2 + 4
Als het p² - 4 was had ik geweten dat het een merkwaardig product was: (p-2)(p+2)
Maar ik weet niet hoe ik het merkwaardig kan oplossen bij zowel p² + 4 als 4p² + 4.
Wat is jouw manier?quote:
Kan iemand hier de juiste berekening van geven? Ik kom wel op de juiste antwoorden maar volgens mij niet op de juiste manier..
Dat is het punt niet. Je dacht hierboven dat jequote:
[..]
Ja de merkwaardige producten ben ik eerder tegengekomen:
4p^2 + 4
Als het p² - 4 was had ik geweten dat het een merkwaardig product was: (p-2)(p+2)
Maar ik weet niet hoe ik het merkwaardig kan oplossen bij zowel p² + 4 als 4p² + 4.
p2 + 1
kon herschrijven als
(p−1)(p+1)
maar dat klopt niet. Je had direct moeten zien dat als (p−1)(p+1) gelijk is aan p2 − 1 dat (p−1)(p+1) dan niet gelijk kan zijn aan p2 + 1.
Oh zo..quote:
[..]
Dat is het punt niet. Je dacht hierboven dat je
p2 + 1
kon herschrijven als
(p−1)(p+1)
maar dat klopt niet. Je had direct moeten zien dat als (p−1)(p+1) gelijk is aan p2 − 1 dat (p−1)(p+1) dan niet gelijk kan zijn aan p2 + 1.
Hoe los je dit op de ''merkwaardigheids'' manier op dan? 4p^2 + 4
Of kan dat niet opgelost worden en is de enige mogelijkheid om in te zien dat alle p's kunnen?
Je kunt p2 + 1 niet schrijven als een product van twee lineaire factoren, althans niet binnen de reële getallen. Maar het is hier voldoende om je te realiseren dat p2 + 1 niet kleiner kan zijn dan 1 en dus dat 4(p2 + 1) niet kleiner kan zijn dan 4. De uitdrukking 4(p2 + 1) is dus positief voor elke (reële) waarde van p.quote:
[..]
Oh zo..
Hoe los je dit op de ''merkwaardigheids'' manier op dan? 4p^2 + 4
Of kan dat niet opgelost worden en is de enige mogelijkheid om in te zien dat alle p's kunnen?
Wiskunde wordt als hulpmiddel gebruikt, net als bij alle andere bèta-opleidingen buiten wiskunde. Dat is niet te vergelijken met wiskunde zelf studeren, je krijgt wat gemeenschappelijke basisvakken en that's it.quote:
[..]
Ik geloof dat jij er de ballen verstand van hebt. Informatica is wel zeker een opleiding waar zeer veel wiskunde behandeld wordt.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Ah kijk, duidelijkquote:
[..]
Wiskunde wordt als hulpmiddel gebruikt, net als bij alle andere bèta-opleidingen buiten wiskunde. Dat is niet te vergelijken met wiskunde zelf studeren, je krijgt wat gemeenschappelijke basisvakken en that's it.
Dan kunnen we er dus wel van uit gaan dat de wiskundekennis van een informatica-student gemiddeld gezien hoger is dan een niet-beta opleiding.
Blijft het natuurlijk een feit dat dit 'middelbareschoolwiskunde' is, een vwo-leerling, die uitblinkt in wiskunde bezit voor dit soort vragen ook genoeg kennis.
Dat is fout. Je weet namelijk helemaal niet of je onbekende p positief of negatief is. Als je bij een ongelijkheid beide leden deelt door een negatief getal, dan klapt het teken van de ongelijkheid om. Maar aangezien je in principe niet weet of je hier door een positief of negatief getal deelt kun je dus ook niet weten of je het ongelijkheidsteken wel of niet om moet klappen. Daarom is je aanpak fout.quote:
[..]
Oeps ik zie het al!
Nee het vetgedrukte niet. Wiskunde blijft een interessant vak.
Ik zou zelf denken p² - 4p < 0 en dus p² < 4p en vervolgens beide kanten delen door p waardoor je krijgt p < 4
Wat je moet doen is eerst de gelijkheid (vergelijking) p2 − 4p = 0 oplossen. Dan vind je p = 0 ∨ p = 4. Vervolgens maak je een tekenschema.
| 1 2 3 | ++++++++++++++++++++0--------------------0++++++++++++++++++++ ____________________|____________________|____________________ 0 4 |
Een tekenschema bestaat uit een getallenlijn waarop je de getallen aangeeft waarvoor je uitdrukking p2 − 4p gelijk is aan nul, hier dus de getallen 0 en 4. Boven deze getallen op de getallenlijn plaats je een 0 om aan te geven dat de waarde van p2 − 4p hier nul is. Verder zet je plustekens boven de getallenlijn daar waar p2 − 4p positief is en mintekens boven de getallenlijn daar waar p2 − 4p negatief is. Nu zie je in één oogopslag in het tekenschema dat p2 − 4p < 0 voor 0 < p < 4.
Uiteraard is het in een eenvoudig geval als dit ook zonder tekenschema direct in te zien dat p2 − 4p alleen negatief kan zijn als p tussen 0 en 4 in ligt: de grafiek van q = p2 − 4p (met p langs de horizontale as en q langs de verticale as) is immers een dalparabool die de p-as snijdt in de punten (0;0) en (4;0). Het deel van de grafiek tussen deze snijpunten ligt onder de p-as, zodat de waarde van q = p2 − 4p negatief is voor waarden van p tussen 0 en 4, en elders niet.
Bij het oplossen van ingewikkelder ongelijkheden kan een tekenschema goede diensten bewijzen. Als je bijvoorbeeld een ongelijkheid hebt met in het linkerlid een breuk waarbij de onbekende zowel in de teller als in de noemer voorkomt terwijl je het rechterlid al hebt herleid op nul, dan kun je twee afzonderlijke tekenschema's maken, namelijk één voor de teller en één voor de noemer, en deze tekenschema's uitgelijnd onder elkaar plaatsen. Als de waarde van de breuk als geheel dan bijvoorbeeld kleiner dan nul moet zijn, dan kan dat alleen hetzij als de teller negatief is en tevens de noemer positief hetzij als de teller positief is en tevens de noemer negatief. Uit het gecombineerde tekenschema van de teller en de noemer kun je dan aflezen voor welke waarden van de onbekende dit het geval is.
[ Bericht 0% gewijzigd door Riparius op 05-05-2014 08:19:12 ]
Laat eerst maar eens zien wat je hebt gedaan.quote:
Kan iemand hier de juiste berekening van geven? Ik kom wel op de juiste antwoorden maar volgens mij niet op de juiste manier..
Hint: voor elke x ∈ R heb je x4 = |x|4 en ook |³√x| = |x|1/3.
Geloof mij nu maar dat je met een informatica studie nog steeds de ballen verstand hebt van wiskunde.quote:
[..]
Ah kijk, duidelijk
Dan kunnen we er dus wel van uit gaan dat de wiskundekennis van een informatica-student gemiddeld gezien hoger is dan een niet-beta opleiding.
Blijft het natuurlijk een feit dat dit 'middelbareschoolwiskunde' is, een vwo-leerling, die uitblinkt in wiskunde bezit voor dit soort vragen ook genoeg kennis.
Fervent tegenstander van het korps lasergamers.
Weten jullie wat er met het volgende bedoelt wordt?:
f (x) = (2x + 4) / (x - 3)
Voor x = 3 wordt de noemer nul, en dan kan f(x) niet berekend worden. Nadert x boven tot 3, dan nadert f(x) tot +∞ , nadert x van onder tot 3, dan nadert f(x) tot -∞ .
Snappen jullie dit? Ik snap het niet echt.. wat maakt het uit als het antwoord op 0 komt bij asymptoten? Dan is het coördinaat van y gewoon 0 toch? Dat kan in principe toch gewoon?
Neem me niet kwalijk voor de vele vragen, maar het is voor mij een voorbereiding voor een intaketoets en dit zijn vrijwel vervaagde onderwerpen voor mij.
f (x) = (2x + 4) / (x - 3)
Voor x = 3 wordt de noemer nul, en dan kan f(x) niet berekend worden. Nadert x boven tot 3, dan nadert f(x) tot +∞ , nadert x van onder tot 3, dan nadert f(x) tot -∞ .
Snappen jullie dit? Ik snap het niet echt.. wat maakt het uit als het antwoord op 0 komt bij asymptoten? Dan is het coördinaat van y gewoon 0 toch? Dat kan in principe toch gewoon?
Neem me niet kwalijk voor de vele vragen, maar het is voor mij een voorbereiding voor een intaketoets en dit zijn vrijwel vervaagde onderwerpen voor mij.
Dat beide lijnen langzamerhand recht naar boven toe gaan wijzen en nooit de x = 3 raken, maar er wel dichtbij tegenaan hangen.quote:
Gaan ze echt beiden recht naar boven? Kijk eens beter.
Verder, wat is het verschil als je van onder ('links') en van boven ('rechts') naar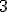
gaat?
Verder, wat is het verschil als je van onder ('links') en van boven ('rechts') naar
Oeps typfout, de één gaat naar boven (rechter) en de linker gaat naar beneden, maar ze raken beide nooit de x =3 (onzichtbare lijn)quote:
Gaan ze echt beiden recht naar boven? Kijk eens beter.
Verder, wat is het verschil als je van onder ('links') en van boven ('rechts') naar
Goeie vraag, heb geen flauw idee.quote:
En waarom zit er een gat (discontinuïteit) bij?
