SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Ik vind die voortbrengende functies helemaal niet handig om een eenvoudige lineaire recursie op te lossen. Met de methode van de zogeheten karakteristieke vergelijking gaat het veel eenvoudiger.quote:Op donderdag 23 januari 2014 23:12 schreef randomo het volgende:
[..]
Het zou kunnen dat je dat geleerd hebt bij wiskunde A (maar het zal waarschijnlijk alleen om lineaire recurrentievergelijkingen gaan, of nog simpelere gevallen). Voor wat ingewikkeldere recurrenties worden vaak voortbrengende functies (bekender onder de Engelse term generating functions) gebruikt, een techniek waarbij je een polynoom met u0, u1, u2, ... als coŽfficiŽnten gebruikt. Best een aparte techniek, maar vaak wel handig.
Voor de geinteresseerden: generatingfunctionology is een gratis pdf'je met een hele zooi informatie over voortbrengende functies (ik moet bekennen dat ik hem zelf nooit uitgelezen heb, maar zelfs alleen het eerste hoofdstuk bevat al erg veel informatie).
Als je de formule x0+x1+x2+...+xn=xn-1/(x+1) kent, kan je gewoon u1, u2, u3, u4, ... etc. uitschrijven (uitdrukken in u0) en kijken of je een patroon ziet. Een beproefde techniek, toegepast door vele beroemde wiskundigen


Ik weet niet in hoeveel detail het bewezen dient te worden, maar je hebt op dit punt enkel bewezen dat de functie niet continu differentieerbaar is. Okee, als je wat stellingen gebruikt heb je ook bewezen dat f niet differentieerbaar is, maar het is wel belangrijk om te beseffen dat de afgeleide van een differentieerbare functie niet continu hoeft te zijn. Ik zou in elk geval direct de definitie van afgeleide toepassen hier.quote:Op donderdag 23 januari 2014 23:31 schreef Miraculously het volgende:
Ik heb de volgende opdracht:
Onderzoek bij de volgende functies voor welke x ze wel gedefinieerd, maar niet differentieerbaar zijn.
f(x) = |x-1|.
Ik weet dat geldt voor f(x) = |x-1| { -(x-1) voor x<1 en x-1 voor x>1 (iemand die weet hoe ik deze stuksgewijs krijg, lukte me niet met LaTex).
Verder weet ik dat het minimum, en dus de knik, zit op het punt (1,0) waar de functie niet differentieerbaar is.
Is het nu voldoende (en klopt het ook) als ik zeg dat:
f'(x) = |x-1|' { -1 voor x<1 en 1 voor x>1
Waardoor we krijgen dat
Waardoor dus f(x)=|x-1| niet differentieerbaar is in het punt x=1.


Voor lineare recursievergelijkingen is inderdaad wat eenvoudiger (er is niet voor niets een heel boek over geschreven), maar volgens mij zijn voortbrengende functies ook nuttig voor ingewikkeldere functies, en hebben ze meer functies dan alleen het oplossen van de recursievergelijking.quote:Op donderdag 23 januari 2014 23:31 schreef Riparius het volgende:
[..]
Ik vind die voortbrengende functies helemaal niet handig om een eenvoudige lineaire recursie op te lossen. Met de methode van de zogeheten karakteristieke vergelijking gaat het veel eenvoudiger.


Die karakteristieke vergelijking staat me nog iets van bij. Misschien komt dat dus wel bij wiskunde D aan de orde.


Als dat alles is wat er van mijn uitleg destijds is blijven hangen, dan is dat niet veel ...quote:Op vrijdag 24 januari 2014 07:13 schreef Amoeba het volgende:
Die karakteristieke vergelijking staat me nog iets van bij. Misschien komt dat dus wel bij wiskunde D aan de orde.
Wil je weten hoe je de gesloten uitdrukking voor de termen van de rij van Fibonacci afleidt met behulp van de voortbrengende functie F(x) = x/(1 − x − x≤) dan moet je Stillwell, Mathematics and Its History, ≥2010, p. 192-194 maar eens raadplegen. Die schrijft het helemaal uit (wat ik hier niet ga doen) en dan zie je dat het niet handig is. Neemt natuurlijk niet weg dat je met voortbrengende functies nog heel wat andere interessante dingen kunt doen.
[ Bericht 0% gewijzigd door Riparius op 24-01-2014 07:51:28 ]


Oh…quote:Op vrijdag 24 januari 2014 07:43 schreef Riparius het volgende:
[..]
Als dat alles is wat er van mijn uitleg destijds is blijven hangen, dan is dat niet veel ...
Wil je weten hoe je de gesloten uitdrukking voor de termen van de rij van Fibonacci afleidt met behulp van de voortbrengende functie F(x) = x/(1 − x − x≤) dan moet je Stillwell, Mathematics and Its History, ≥2010, p. 192-194 maar eens raadplegen. Die schrijft het helemaal uit (wat ik hier niet ga doen) en dan zie je dat het niet handig is. Neemt natuurlijk niet weg dat je met voortbrengende functies nog heel wat andere interessante dingen kunt doen.
Mooie post wel. Nog eens oprakelen dan maar.


Bedankt voor je antwoord.quote:Op vrijdag 24 januari 2014 00:11 schreef thabit het volgende:
[..]
Ik weet niet in hoeveel detail het bewezen dient te worden, maar je hebt op dit punt enkel bewezen dat de functie niet continu differentieerbaar is. Okee, als je wat stellingen gebruikt heb je ook bewezen dat f niet differentieerbaar is, maar het is wel belangrijk om te beseffen dat de afgeleide van een differentieerbare functie niet continu hoeft te zijn. Ik zou in elk geval direct de definitie van afgeleide toepassen hier.
Met de definitie van de afgeleide bedoel je f'(a) = limx→a (f(x) - f(a)) / (x - a) neem ik aan?


Gebruik de ε,δ definitie van de limiet om te laten zien dat limh→0 (f(1+h) − f(1))/h niet bestaat, dan heb je bewezen dat f niet differentieerbaar is in het punt x = 1. Verder wijst Thabit er terecht op dat je niet zomaar (impliciet of expliciet) aan mag nemen dat de afgeleide continu is in die punten waar je functie wel differentieerbaar is.quote:Op vrijdag 24 januari 2014 19:46 schreef Miraculously het volgende:
[..]
Bedankt voor je antwoord.
Met de definitie van de afgeleide bedoel je f'(a) = limx→a (f(x) - f(a)) / (x - a) neem ik aan?
[ Bericht 0% gewijzigd door Riparius op 25-01-2014 02:35:13 ]


Dat voorbeeld (een gesloten uitdrukking voor de termen van de rij van Fibonacci) staat overigens ook in de link die ik gaf. Ze gaan er daar wel redelijk snel doorheen (in ongeveer een bladzijde). Waarmee ik overigens niet bedoel dat het een handige manier is.quote:Op vrijdag 24 januari 2014 07:43 schreef Riparius het volgende:
[..]
Als dat alles is wat er van mijn uitleg destijds is blijven hangen, dan is dat niet veel ...
Wil je weten hoe je de gesloten uitdrukking voor de termen van de rij van Fibonacci afleidt met behulp van de voortbrengende functie F(x) = x/(1 − x − x≤) dan moet je Stillwell, Mathematics and Its History, ≥2010, p. 192-194 maar eens raadplegen. Die schrijft het helemaal uit (wat ik hier niet ga doen) en dan zie je dat het niet handig is. Neemt natuurlijk niet weg dat je met voortbrengende functies nog heel wat andere interessante dingen kunt doen.
Ik moet bekennen dat ik zelf ook weer even moest nadenken hoe die methode van de karakteristieke vergelijking ook al weer werkte. Maar eigenlijk is het heel simpel: je neemt aan dat xn een oplossing is, daaruit vindt je een kwadratische vergelijking met (hopelijk) twee oplossingen. Door een lineaire combinatie van deze twee oplossingen te maken kan je een nieuwe oplossing maken, die voldoet aan een randvoorwaarde. Als je alleen de eerste stap onthoudt (het aannemen dat er een oplossing van de vorm xn is), volgt de rest vrij natuurlijk.


De vierkantsvergelijking die je krijgt bij een homogene tweede orde lineaire recursie met constante coŽfficiŽnten heeft altijd twee oplossingen. Het wordt alleen iets lastiger als de twee oplossingen samenvallen. Wat je dan moet doen is niet helemaal triviaal, en dat heb ik destijds met opzet ook niet uitgelegd. Ik had gehoopt dat Amoeba daar wel een kritische vraag over zou stellen, maar dat gebeurde niet ...quote:Op vrijdag 24 januari 2014 20:31 schreef randomo het volgende:
[..]
Dat voorbeeld (een gesloten uitdrukking voor de termen van de rij van Fibonacci) staat overigens ook in de link die ik gaf. Ze gaan er daar wel redelijk snel doorheen (in ongeveer een bladzijde). Waarmee ik overigens niet bedoel dat het een handige manier is.
Ik moet bekennen dat ik zelf ook weer even moest nadenken hoe die methode van de karakteristieke vergelijking ook al weer werkte. Maar eigenlijk is het heel simpel: je neemt aan dat xn een oplossing is, daaruit vindt je een kwadratische vergelijking met (hopelijk) twee oplossingen. Door een lineaire combinatie van deze twee oplossingen te maken kan je een nieuwe oplossing maken, die voldoet aan een randvoorwaarde. Als je alleen de eerste stap onthoudt (het aannemen dat er een oplossing van de vorm xn is), volgt de rest vrij natuurlijk.


Met voortbrengende functies kan je laten zien dat als de karakteristieke vergelijking kwadratisch is en een dubbel nulpunt heeft (dus van de vorm (x - c)2 = 0 is), een gesloten uitdrukking voor de recursie ak = kck-1a1 - (k - 1)cka0 is. Maar ik verwacht stiekem wel dat Riparius nog met een andere manier op de proppen komtquote:Op vrijdag 24 januari 2014 20:42 schreef Riparius het volgende:
[..]
De vierkantsvergelijking die je krijgt bij een homogene tweede orde lineaire recursie met constante coŽfficiŽnten heeft altijd twee oplossingen. Het wordt alleen iets lastiger als de twee oplossingen samenvallen. Wat je dan moet doen is niet helemaal triviaal, en dat heb ik destijds met opzet ook niet uitgelegd. Ik had gehoopt dat Amoeba daar wel een kritische vraag over zou stellen, maar dat gebeurde niet ...
Ik bedenk me nu pas dat je natuurlijk ook een kwadratische vergelijking kan hebben met alleen complexe nulpunten, dat is denk ik ook een moeilijkheid als je de methode van de karakteristieke vergelijking gebruikt (of niet? Ik denk er morgen misschien nog maar eens over na, het is inmiddels al half twee hier...)
Ik meen me ook een dergelijke uitdrukking te herinneren voor het oplossen van lineaire homogene differentiaalvergelijkingen met constante coŽfficiŽnten. Als je een differentiaalvergelijking hebt van de vorm:
x'' = ax' + bx
kan je oplossingen van de vorm eλx veronderstellen, zodat je een karakteristiek polynoom krijgt:
λ2eλx = ac eλx + beλx
delen door eλx en alles naar de linkerkant brengen geeft:
λ2 - aλ - b = 0
Het idee is nu hetzelfde: vindt de twee oplossingen, door ze te combineren kan je een oplossing met de gewenste randvoorwaarde vinden. Ik meen me te herinneren (verbeter me als ik ernaast zit) dat als je een oplossing λ vindt met multipliciteit 2, je ipv van eλx, je xeλx en eλx als oplossingen vindt.
Ik blijf het allemaal een beetje mysterieus vinden...
[ Bericht 1% gewijzigd door randomo op 25-01-2014 10:31:31 ]


Zeer veel dank!!quote:Op woensdag 22 januari 2014 22:33 schreef Riparius het volgende:
[..]
Een klassiek meetkundig bewijs verloopt volgens een vast stramien: Gegeven: ..., Te bewijzen: ..., Bewijs: ..., en eindigt natuurlijk met QED (Quod Erat Demonstrandum 'hetgeen te bewijzen was').
Je moet dus eerst bedenken wat je precies als gegeven wil veronderstellen (ja, een ruit natuurlijk) en wat je dan precies wil aantonen. Begin met te bedenken wat de definitie is van een ruit. Dat is niet evident, want er worden verschillende definities gehanteerd voor een ruit. In oudere meetkundeboeken (en bijvoorbeeld ook nog in de Franse Wikipedia) definieert men een ruit als een parallellogram waarvan twee aanliggende zijden gelijk zijn, maar een ruit wordt tegenwoordig meestal gedefinieerd als een vierhoek met vier gelijke zijden (zo bijvoorbeeld in de Nederlandse en de Engelse Wikipedia). De gekozen definitie heeft uiteraard consequenties, want als je de oude definitie hanteert, dan is de eigenschap dat een ruit vier gelijke zijden heeft een stelling, evenals het omgekeerde, namelijk dat een vierhoek met vier gelijke zijden een ruit is. En, vice versa, met de nieuwe definitie van een ruit is de bewering dat een ruit een parallellogram is weer een stelling.
Maar goed, teken een plaatje van een ruit en duid daarbij de hoekpunten aan met de letters A t/m D:
[ afbeelding ]
Teken ook de beide diagonalen AC en BD van de ruit.
Het is niet voldoende om alleen een plaatje te tekenen, je moet hier ook in woorden bij aangeven wat je precies als zijnde gegeven veronderstelt:
Gegeven: een ruit ABCD met diagonalen AC en BD.
Vervolgens moet je precies formuleren wŠt je nu eigenlijk wil bewijzen, waarbij je uiteraard kunt (en moet) refereren aan hetgeen je als gegeven hebt verondersteld. In dit geval zou je dus kunnen zeggen:
Te bewijzen: ∠BAC = ∠CAD.
Nu komt het echte werk. Bedenk dat je bij een bewijs een beroep mag doen op eerder bewezen stellingen.
Bewijs: Op grond van de definitie van een ruit is AB = BC, zodat driehoek ABC gelijkbenig is. In een gelijkbenige driehoek zijn de basishoeken gelijk, zodat
∠BAC = ∠BCA.
Aangezien een ruit een parallellogram is en in een parallellogram overstaande zijden evenwijdig zijn, is zijde BC evenwijdig aan zijde AD. Dus zijn ∠BCA en ∠CAD verwisselende binnenhoeken (Z-hoeken) en deze zijn ook gelijk, dus
∠BCA = ∠CAD.
Ergo
∠BAC = ∠CAD,
QED
Het bewijs voor elk van de drie andere hoekpunten verloopt uiteraard geheel analoog.
Het is me een stuk duidelijker geworden door deze uitleg.


Laten we eens uitgaan van een rij {un}, n∈ N0 met louter reŽle termen die aan een homogene lineaire tweede orde recursie met constante en reŽle coŽfficiŽnten voldoet, en welquote:Op zaterdag 25 januari 2014 10:17 schreef randomo het volgende:
Ik blijf het allemaal een beetje mysterieus vinden...Kan iemand me iets meer inzicht bijbrengen?
(1) a·un + b·un−1 + c·un−2 = 0
Hierbij moeten we a ≠ 0 en tevens c ≠ 0 veronderstellen, aangezien we anders geen tweede orde recursie hebben.
Zoals bekend kunnen we in beginsel gesloten uitdrukkingen vinden voor de algemene term un van rijen die aan het recursievoorschrift (1) voldoen door op zoek te gaan naar meetkundige rijen die aan dit voorschrift voldoen. Hebben we een meetkundige rij {un} met als eerste term u0 en reden λ, dan is
(2) un = u0·λn
Substitutie van (2) in geeft voor n > 1
(3) u0·λn−2(aλ2 + bλ + c) = 0
Nu is het duidelijk dat un = 0, i.e. een rij die uit louter nullen bestaat, een triviale oplossing is van het recursievoorschrift (1) en dat we daarom op grond van (2) zowel u0 ≠ 0 als λ ≠ 0 moeten veronderstellen om andere oplossingen naast deze triviale oplossing te vinden. Maar dan kan uitsluitend aan (3) worden voldaan als de uitdrukking tussen haakjes gelijk is aan nul, dus
(4) aλ2 + bλ + c = 0
Dit is de zogeheten karakteristieke vergelijking van het recursievoorschrift (1). We noemen het polynoom
(5) P(λ) = aλ2 + bλ + c
ook het karakteristieke polynoom van het recursievoorschrift (1). Nu is (4) een vierkantsvergelijking in λ, en zoals bekend wordt de aard van de nulpunten van P(λ) en daarmee van de oplossingen van (4) bepaald door de discriminant
(6) D = b2 − 4ac
van dit polynoom. We onderscheiden nu drie mogelijkheden.
1. D > 0. Nu heeft P(λ) twee verschillende reŽle nulpunten λ1 en λ2 en zijn de meetkundige rijen gedefinieerd door un = u0·λ1n en un = u0·λ2n twee (lineair onafhankelijke) oplossingen van (1). En omdat elke lineaire combinatie {cn} met cn = α·an + β·bn van twee rijen {an} en {bn} die voldoen aan (1) ook weer voldoet aan (1) krijgen we als algemene oplossing van het recursievoorschrift
(7) un = α·λ1n+ β·λ2n
waarin α en β willekeurige (reŽle) constanten zijn. Het is eenvoudig na te gaan dat (7) ook inderdaad de volledige oplossing geeft van het recursievoorschrift (1). Een rij die voldoet aan een tweede orde recursie ligt volledig vast als twee opeenvolgende termen van de rij zijn gegeven. Welnu, substitutie in (7) van twee opeenvolgende termen van een specifieke rij die aan (1) voldoet levert een stelsel van twee lineaire vergelijkingen in α en β en dit stelsel bezit een unieke oplossing aangezien uit c ≠ 0 in (1) volgt dat λ1 ≠ 0 en tevens λ2 ≠ 0, terwijl uit D ≠ 0 volgt dat λ1 ≠ λ2, zodat de determinant van het stelsel ongelijk is aan nul.
2. D < 0. Nu heeft P(λ) twee toegevoegd complexe nulpunten λ1 en λ2 maar de situatie verschilt niet wezenlijk van die voor D > 0. Ook nu geldt dat (7) de algemene oplossing geeft van het recursievoorschrift (1), en ook nu levert substitutie in (7) van twee opeenvolgende termen van een specifieke rij een stelsel van twee lineaire vergelijkingen in α en β met een unieke oplossing. Echter, niet alleen λ1 en λ2 maar ook α en β zijn nu in het algemeen (toegevoegd) complex, zodat het niet mogelijk is een gesloten algebraÔsche uitdrukking voor de algemene term van de recursieve rij te geven zonder gebruik van complexe getallen, en dat terwijl alle termen van de rij zelf wel degelijk reŽel zijn. Maar, zoals ik wel eens heb laten zien, is het in dit geval altijd mogelijk een goniometrische uitdrukking te geven voor algemene term van de rij zonder gebruik van complexe getallen.
3. D = 0. Nu heeft P(λ) ťťn reŽel nulpunt met multipliciteit 2, dat ik aan zal geven met λ0. Aangezien λ0 voldoet aan (4) is het duidelijk dat
(8) un = α·λ0n
met een willekeurige α in ieder geval een oplossing is van het recursievoorschrift (1). Maar het is evenzeer duidelijk dat (8) nu niet de volledige oplossing kan zijn van (1) omdat we bij het recursievoorschrift (1) de waarden van u0 en u1 steeds vrij kunnen kiezen, terwijl (8) alleen een oplossing biedt als u1 = λ0u0.
Een elegante methode om toch de volledige oplossing van (1) te verkrijgen als D = 0 berust op het gebruik van differentiaalrekening. Daarvoor hebben we de volgende stelling nodig:
Als een niet-constant polynoom P(x) een nulpunt x = x0 heeft met een multipliciteit m > 1, dan is P(i)(x0) = 0 voor i = 1 .. (m − 1) terwijl P(m)(x0) ≠ 0.
Het bewijs van deze stelling gaat het eenvoudigst als we eerst even twee lemmata bewijzen.
Lemma 1. Als een niet-constant polynoom P(x) een enkelvoudig nulpunt x = x0 heeft, dan is P'(x0) ≠ 0.
Bewijs: volgens de factorstelling volgt uit P(x0) = 0 dat P(x) een factor (x − x0) bevat zodat P(x) = (x −x0)·Q(x). Aangezien x = x0 een enkelvoudig nulpunt is van P(x) kan het polynoom Q(x) geen verdere factoren (x − x0) bevatten zodat, wederom volgens de factorstelling, Q(x0) ≠ 0. De afgeleide van P(x) = (x −x0)·Q(x) is P'(x) = Q(x) + (x − x0)·Q'(x) zodat P'(x0) = Q(x0) + 0·Q'(x0) = Q(x0) ≠ 0, QED.
Lemma 2. Als een niet-constant polynoom P(x) een nulpunt x = x0 heeft met een multipliciteit m > 1 dan heeft de afgeleide P'(x) een nulpunt x = x0 met een multipliciteit (m − 1).
Bewijs: aangezien P(x) een nulpunt x = x0 heeft met multipliciteit m > 1 is P(x) = (x − x0)m·Q(x) waarbij het polynoom Q(x) geen verdere factoren (x − x0) bevat zodat volgens de factorstelling Q(x0) ≠ 0. De afgeleide van P(x) = (x − x0)m·Q(x) is P'(x) = m·(x − x0)m−1·Q(x) + (x − x0)m·Q'(x) waarvoor we kunnen schrijven P'(x) = (x − x0)m−1·(m·Q(x) + (x − x0)·Q'(x)). Voor x = x0 is de factor (m·Q(x) + (x − x0)·Q'(x)) gelijk aan m·Q(x0) ≠ 0 zodat (m·Q(x) + (x − x0)·Q'(x)) volgens de factorstelling geen factor (x − x0) bevat en de multipliciteit van het nulpunt x = x0 van P'(x) dus gelijk is aan (m − 1), QED.
Het bewijs van bovenstaande stelling is nu uiteraard eenvoudig: heeft een niet-constant polynoom P(x) een nulpunt x = x0 met multipliciteit m > 1, dan geeft (herhaalde) toepassing van lemma 2 dat P(i)(x) voor i = 1 .. (m − 1) een nulpunt x = x0 heeft met een multipliciteit (m − i), zodat P(m−1)(x) een enkelvoudig nulpunt x = x0 heeft. En volgens lemma 1 is dan P(m)(x0) ≠ 0, QED.
Goed, nu de volledige oplossing van (1) als D = 0. Vermenigvuldigen we beide leden van (5) met λn−2, dan hebben we voor n > 1
(9) a·λn + b·λn−1 + c·λn−2 = λn−2·P(λ)
DifferentiŽren naar λ geeft nu
(10) a·n·λn−1 + b·(n−1)·λn−2 + c·(n−2)·λn−3 = (n−2)·λn−3·P(λ) + λn−2·P'(λ)
En beide leden vermenigvuldigen met λ geeft dan
(11) a·n·λn + b·(n−1)·λn−1 + c·(n−2)·λn−2 = (n−2)·λn−2·P(λ) + λn−1·P'(λ)
Nu is λ = λ0 een nulpunt van P(λ) met multipliciteit 2, zodat niet alleen P(λ0) = 0 maar tevens P'(λ0) = 0. Substutie van λ = λ0 in (11) geeft dus
(12) a·n·λ0n + b·(n−1)·λ0n−1 + c·(n−2)·λ0n−2 = 0
zodat we kunnen concluderen dat un = n·λ0n aan het recursievoorschrift (1) voldoet. Eerder vonden we al dat un = λ0n voldoet, zodat ook elke lineaire combinatie van deze oplossingen aan het recursievoorschrift voldoet en we dus krijgen
(13) un = (α + β·n)·λ0n
Het is weer gemakkelijk na te gaan dat deze oplossing inderdaad volledig is. Substitutie in (13) van twee opeenvolgende termen van een specifieke rij die aan (1) voldoet levert een stelsel van twee lineaire vergelijkingen in α en β en dit stelsel bezit een unieke oplossing aangezien uit c ≠ 0 in (1) volgt dat λ0 ≠ 0 zodat de determinant van het stelsel ongelijk is aan nul.
Het aardige van deze methode is dat deze eenvoudig is te generaliseren naar homogene lineaire recursies met constante coŽfficiŽnten van hogere ordes. Heeft het karakteristieke polynoom P(λ) van zo'n hogere orde recursie van orde N namelijk een meervoudig nulpunt λ = λ0 met multipliciteit m, dan kun je door P(λ) te vermenigvuldigen met λn−N en daarna telkens om beurten te differentiŽren en weer te vermenigvuldigen met λ gemakkelijk laten zien dat naast un = λ0n ook un = ni·λ0n voor i = 1 .. (m − 1) een oplossing geeft van de recursie. Zo geeft elk meervoudig nulpunt met een multipliciteit m dus precies m lineair onafhankelijke oplossingen.
Wil je niet gebruik maken van differentiaalrekening, dan is er in ieder geval voor tweede orde recursies waarbij de discriminant van de karakteristieke vergelijking gelijk is aan nul ook een goed bruikbare elementaire methode die bekend staat als de variatie van de constante. Het idee hierbij is dat je uitgaat van (8) maar dat je veronderstelt dat α niet constant is maar een functie van n. Dat wil dus zeggen dat je een rij {αn} zoekt zodanig dat
(14) un = αn·λ0n
een oplossing is van de recursie (1). Welnu, invullen van (14) in (1) geeft voor n > 1
(15) λ0n−2(a·αn·λ02 + b·αn−1·λ0 + c·αn−2) = 0
en aangezien λ0 ≠ 0 geeft dit
(16) a·αn·λ02 + b·αn−1·λ0 + c·αn−2 = 0
Nu weten we echter ook dat λ0 = −b/2a (en dus b ≠ 0 aangezien λ0 ≠ 0). Substitutie hiervan in (16) en gebruik maken van D = b2 − 4ac = 0 (en dus 4ac = b2) levert dan na wat herleiding
(17) αn − αn−1 = αn−1 − αn−2
In woorden: het verschil tussen elk tweetal opeenvolgende termen van de rij {αn} is constant. De rij {αn} is dus een willekeurige rekenkundige rij, en de algemene gedaante van αn is dus
(18) αn = α + n·β
waarbij α en β willekeurige constanten zijn. Substitutie van (18) in (14) geeft nu
(19) un = (α + n·β)·λ0n
en dit stemt geheel overeen met de eerder gevonden algemene oplossing (13).
That's all.


Wat snap je er niet aan? Wat snap je al wel?quote:Op zondag 26 januari 2014 12:17 schreef Beverwijker het volgende:
http://tinypic.com/r/11snpc2/5
Iemand die mij vraag 12 kan uitleggen.
Het gaat hier om een driehoek met een rechte hoek. Gegeven is de lengte van ťťn van de zijdes die aan deze rechte hoek grenst (10). De andere zijde die aan de rechte hoek grenst wordt lengte a gesteld. Het gevraagde is de lengte van de langste zijde, dat is (op grond van de driehoeksongelijkheid) de schuine zijde van deze driehoek. Kun je hier iets mee? Hint: Pythagoras.
Als je dat doorhebt weet je waar de formule vandaan komt. De opdracht is simpeler: je moet drie keer een waarde voor a invullen in de formule.


Stel je hebt twee open sets, zeg maar 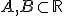 . Is het Cartesian Product
. Is het Cartesian Product 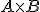 dan ook open? En zoja, hoe kan ik het beste hiervan een bewijs leveren?
dan ook open? En zoja, hoe kan ik het beste hiervan een bewijs leveren?
Edit: Zie hier het antwoord + bewijs: http://math.stackexchange.com/q/653106/96700
[ Bericht 17% gewijzigd door Novermars op 27-01-2014 16:06:44 ]
Edit: Zie hier het antwoord + bewijs: http://math.stackexchange.com/q/653106/96700
[ Bericht 17% gewijzigd door Novermars op 27-01-2014 16:06:44 ]


Top! Zoals gewoonlijk weer een uitstekende uitlegquote:
Die stelling was inderdaad uiteindelijk de missing link
Veel dank en hulde!quote:Als een niet-constant polynoom P(x) een nulpunt x = x0 heeft met een multipliciteit m > 1, dan is P(i)(x0) = 0 voor i = 1 .. (m − 1) terwijl P(m)(x0) ≠ 0.


Dit is metawiskundig gezien wel een interessante vraag, want hoe definieer je de topologie op RxR? Enerzijds kun je de Euclidische metriek nemen en van daar uit werken. Anderzijds bestaat er ook een categorie-theoretische definitie van producten en kun je bewijzen dat producten bestaan in de categorie van topologische ruimten. De twee topologieŽn die je zo krijgt blijken hetzelfde te zijn, iets wat niet vanzelfsprekend is!quote:Op zondag 26 januari 2014 22:03 schreef Novermars het volgende:
Stel je hebt twee open sets, zeg maar. Is het Cartesian Product
dan ook open? En zoja, hoe kan ik het beste hiervan een bewijs leveren?
Edit: Zie hier het antwoord + bewijs: http://math.stackexchange.com/q/653106/96700


Ik krijg koppijn van dit vraagstuk
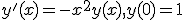
Nu moet ik dit oplossen mbv machtreeksen, vervolgens de convergentiestraal van de gevonden machtreeks bepalen en daarna een gesloten uitdrukking voor die machtreeks geven.
Tot nu toe was ik zo ver:
Waarbij ik zeker weet dat die onderste vergelijking niet klopt, immers gaat delen door k+3 na de eerste stap al fout..
Wat doe ik fout / wat mis ik?
[ Bericht 0% gewijzigd door #ANONIEM op 28-01-2014 21:48:45 ]
Nu moet ik dit oplossen mbv machtreeksen, vervolgens de convergentiestraal van de gevonden machtreeks bepalen en daarna een gesloten uitdrukking voor die machtreeks geven.
Tot nu toe was ik zo ver:
Waarbij ik zeker weet dat die onderste vergelijking niet klopt, immers gaat delen door k+3 na de eerste stap al fout..
Wat doe ik fout / wat mis ik?
[ Bericht 0% gewijzigd door #ANONIEM op 28-01-2014 21:48:45 ]


Je mist een accentje.quote:Op dinsdag 28 januari 2014 21:40 schreef Amoeba het volgende:
Ik krijg koppijn van dit vraagstuk
Nu moet ik dit oplossen mbv machtreeksen, vervolgens de convergentiestraal van de gevonden machtreeks bepalen en daarna een gesloten uitdrukking voor die machtreeks geven.
Tot nu toe was ik zo ver:
[ afbeelding ]
Waarbij ik zeker weet dat die onderste vergelijking niet klopt, immers gaat delen door k+3 na de eerste stap al fout..
Wat doe ik fout / wat mis ik?


Excuus, ik heb er eentje te veel gezet.quote:
http://www.win.tue.nl/~gprokert/opcoll14.pdf
Opgave 3
[ Bericht 6% gewijzigd door #ANONIEM op 28-01-2014 21:49:42 ]


Ja die is gegarandeerd fout. Ik weet niet hoe ik de coŽfficiŽnten van mijn expansie terugkrijg.quote:Op dinsdag 28 januari 2014 21:50 schreef thabit het volgende:
Ik snap niet hoe je bij die laatste formule komt.


Ja, dat wil zeggen:quote:Op dinsdag 28 januari 2014 21:55 schreef thabit het volgende:
Er staat ck = -ck-3/k, dus er zal iets met faculteiten in de noemers moeten komen.
met
quote:


Maar niet in de eerste, die is namelijk 1.quote:Op dinsdag 28 januari 2014 22:00 schreef thabit het volgende:
Nou, in elk van die factoren zit telkens een factor 3. Haal die er eerst maar eens uit.


1 is het lege product, dus die heeft geen factoren.quote:Op dinsdag 28 januari 2014 22:02 schreef Amoeba het volgende:
[..]
Maar niet in de eerste, die is namelijk 1.


Okay.quote:Op dinsdag 28 januari 2014 22:02 schreef thabit het volgende:
[..]
1 is het lege product, dus die heeft geen factoren.
Maar mijn berekening tot dusverre,
met
is juist?
Mijn vraag komt er echt op neer wat (ak) in gesloten vorm is..
[ Bericht 0% gewijzigd door #ANONIEM op 28-01-2014 22:08:36 ]


Eerste correctie bleek goed denk ik.
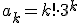
=>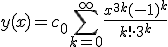
Volgens Cauchy's Ratio Test convergeert y(x) op heel R, en dan nu die gesloten uitdrukking nog. Left for tomorrow I suppose.
Thabit, mijn dank.
Ik ben natuurlijk vergeten dat c0 ongelijk 0 is, anders is alles flauw.
[ Bericht 33% gewijzigd door #ANONIEM op 28-01-2014 22:37:57 ]
=>
Volgens Cauchy's Ratio Test convergeert y(x) op heel R, en dan nu die gesloten uitdrukking nog. Left for tomorrow I suppose.
Thabit, mijn dank.
Ik ben natuurlijk vergeten dat c0 ongelijk 0 is, anders is alles flauw.
[ Bericht 33% gewijzigd door #ANONIEM op 28-01-2014 22:37:57 ]


Jij bedoelt met ak iets anders dan in de oorspronkelijke opgave, en dat moet je natuurlijk niet doen. De oplossing van je DV is uiteraard y(x) = e−x≥/3, dus het is gemakkelijk na te gaan wat de coŽfficiŽnten van je machtreeks zouden moeten zijn.quote:


http://imgur.com/CS9i9Y4
Hoe bewijs ik dat de functierij niet uniform convergeert bij b)? De puntsgewijze functie is 0 voor alle x in R, dus ik kan niet het argument gebruiken dat de limiet functie niet continu is... Ik zat zelf verder nog te denken aan de supremum norm, maar dan lukt de maximale waarde bepalen niet...
Hoe bewijs ik dat de functierij niet uniform convergeert bij b)? De puntsgewijze functie is 0 voor alle x in R, dus ik kan niet het argument gebruiken dat de limiet functie niet continu is... Ik zat zelf verder nog te denken aan de supremum norm, maar dan lukt de maximale waarde bepalen niet...


Het gaat mis rond het punt 0. Kijk eens wat er gebeurt als je bijvoorbeeld x=1/n neemt.quote:Op woensdag 29 januari 2014 15:43 schreef spacer730 het volgende:
http://imgur.com/CS9i9Y4
Hoe bewijs ik dat de functierij niet uniform convergeert bij b)? De puntsgewijze functie is 0 voor alle x in R, dus ik kan niet het argument gebruiken dat de limiet functie niet continu is... Ik zat zelf verder nog te denken aan de supremum norm, maar dan lukt de maximale waarde bepalen niet...


Als x=1/n, dan gaat de functierij voor n->oneindig dus naar sin(1)/e, dus niet continu dus geen uniforme convergentie? Dan zou de puntsgewijze limietfunctie dus ook niet 0 zijn voor alle xquote:Op woensdag 29 januari 2014 18:28 schreef thenxero het volgende:
[..]
Het gaat mis rond het punt 0. Kijk eens wat er gebeurt als je bijvoorbeeld x=1/n neemt.


Je moet gewoon netjes de definities toepassen van puntsgewijze convergentie en uniforme convergentie. Puntsgewijze convergentie van je functierij {fn} naar een functie f* op R betekent dat je voor elke x ∈ R hebtquote:Op woensdag 29 januari 2014 19:05 schreef spacer730 het volgende:
[..]
Als x=1/n, dan gaat de functierij voor n->oneindig dus naar sin(1)/e, dus niet continu dus geen uniforme convergentie? Dan zou de puntsgewijze limietfunctie dus ook niet 0 zijn voor alle x
limn→∞ fn(x) = f*(x)
Bij a) word je gevraagd na te gaan dat dit inderdaad het geval is en f* te bepalen.
Uniforme convergentie van je functierij {fn} naar de bij a) bepaalde functie f* op R zou inhouden dat er voor elke ε > 0 een N ∈ N bestaat zodanig dat voor elke n > N en elke x ∈ R geldt
| fn(x) − f*(x) | < ε
Bij b) word je gevraagd aan te tonen dat dit niet het geval is voor jouw functierij {fn} en de bij a) bepaalde functie f*.


Voor de liefhebbers, op Coursera is een course 'Functional Analysis' begonnen. https://class.coursera.org/functionalanalysis-001
Het begint nog redelijk simpel, zeker de filmpjes. Maar de supplementaire PDF is toch wel redelijk pittig.
Het begint nog redelijk simpel, zeker de filmpjes. Maar de supplementaire PDF is toch wel redelijk pittig.


Fijne site, maar niet heus. Ik zie niet in waarom zoiets weggestopt moet worden achter een login, en mijn browser loopt ook nog eens vast op een script op de site wanneer ik een lijst probeer op te vragen van het cursusaanbod.quote:Op woensdag 29 januari 2014 20:04 schreef Novermars het volgende:
Voor de liefhebbers, op Coursera is een course 'Functional Analysis' begonnen. https://class.coursera.org/functionalanalysis-001
Het begint nog redelijk simpel, zeker de filmpjes. Maar de supplementaire PDF is toch wel redelijk pittig.


https://www.dropbox.com/s(...)alysis-week01-V2.pdfquote:Op woensdag 29 januari 2014 20:54 schreef Riparius het volgende:
[..]
Fijne site, maar niet heus. Ik zie niet in waarom zoiets weggestopt moet worden achter een login, en mijn browser loopt ook nog eens vast op een script op de site wanneer ik een lijst probeer op te vragen van het cursusaanbod.
Syllabus:
Week 1: Topology; continuity and convergence of a sequence in a topological space.
Week 2: Metric and normed spaces; completeness
Week 3: Banach spaces; linear continuous functions; weak topology
Week 4: Hilbert spaces; The Riesz representation theorem
Week 5: The Lax-Milgram Lemma
Week 6: Lp spaces; Fischer-Riesz
Week 7: Sobolev spaces
Week 8: Use of functional analysis for Partial Differential Equations


Haha, ik droomde vannacht dat Riparius weer een uitlegpost had gemaakt (of twee eigenlijk, want het paste niet in een post). Ik heb zo tentamen, zal daar wel door komen denk ik 


Zoiets, maar dit is nog wat te vaag (en ook twijfelachtig, de puntsgewijze limiet is overal 0 dus je hebt wel continuÔteit). Mijn punt was eigenlijk: voordat je een bewijs gaat opstellen wil je eerst kijken naar wat er (in dit geval) misgaat. Als je eenmaal geÔdentificeerd hebt dat het rond x=0 misgaat (wat je dus kan inzien door x=1/n in te vullen), kan je een rigoureus bewijs geven.quote:Op woensdag 29 januari 2014 19:05 schreef spacer730 het volgende:
[..]
Als x=1/n, dan gaat de functierij voor n->oneindig dus naar sin(1)/e, dus niet continu dus geen uniforme convergentie? Dan zou de puntsgewijze limietfunctie dus ook niet 0 zijn voor alle x
Neem epsilon = sin(1)/e. Laat N in N willekeurig zijn. Neem n=N en x=1/n, dan |f_n(x)-0|>= epsilon. Klaar.


quote:Op woensdag 29 januari 2014 19:51 schreef Riparius het volgende:
[..]
Je moet gewoon netjes de definities toepassen van puntsgewijze convergentie en uniforme convergentie. Puntsgewijze convergentie van je functierij {fn} naar een functie f* op R betekent dat je voor elke x ∈ R hebt
limn→∞ fn(x) = f*(x)
Bij a) word je gevraagd na te gaan dat dit inderdaad het geval is en f* te bepalen.
Uniforme convergentie van je functierij {fn} naar de bij a) bepaalde functie f* op R zou inhouden dat er voor elke ε > 0 een N ∈ N bestaat zodanig dat voor elke n > N en elke x ∈ R geldt
| fn(x) − f*(x) | < ε
Bij b) word je gevraagd aan te tonen dat dit niet het geval is voor jouw functierij {fn} en de bij a) bepaalde functie f*.
Ah natuurlijk je moet gewoon de logische ontkenning van de definitie bewijzen, bedankt beiden!quote:Op donderdag 30 januari 2014 17:45 schreef thenxero het volgende:
[..]
Zoiets, maar dit is nog wat te vaag (en ook twijfelachtig, de puntsgewijze limiet is overal 0 dus je hebt wel continuÔteit). Mijn punt was eigenlijk: voordat je een bewijs gaat opstellen wil je eerst kijken naar wat er (in dit geval) misgaat. Als je eenmaal geÔdentificeerd hebt dat het rond x=0 misgaat (wat je dus kan inzien door x=1/n in te vullen), kan je een rigoureus bewijs geven.
Neem epsilon = sin(1)/e. Laat N in N willekeurig zijn. Neem n=N en x=1/n, dan |f_n(x)-0|>= epsilon. Klaar.


Ik heb 2 matrices van 2x2, E1 and E2. Nu heb ik de regio's E1*x >= 0 en E2*x >= 0 is het mogelijk, zo ja hoe, om de intersectie te bepalen hiervan? Dus een nieuwe matrix F die de intersectie beschrijft F*x >= 0?


In een deel van de uitwerking van een som staat dit:
10^(2*logD)
(10^logD)2
Ik snap niet hoe het kan dat het eerst keer 2 is en vervolgens tot de macht 2. Is er misschien een tussenstap gedaan?
10^(2*logD)
(10^logD)2
Ik snap niet hoe het kan dat het eerst keer 2 is en vervolgens tot de macht 2. Is er misschien een tussenstap gedaan?


Weet je zeker dat de tweede regel niet 10log(D^2) moet zijn? xlog(y) is immers log(y^x)quote:Op maandag 3 februari 2014 14:18 schreef GoodnightNeverland het volgende:
In een deel van de uitwerking van een som staat dit:
10^(2*logD)
(10^logD)2
Ik snap niet hoe het kan dat het eerst keer 2 is en vervolgens tot de macht 2. Is er misschien een tussenstap gedaan?


Ik ga in mei een staatsexamen wiskunde B VWO doen waarin ik mij voorbereid d.m.v. de Getal en Ruimte reeks. Dit is mijn eerste post hier, en ik heb zo'n 10 minuten geprobeerd mijn functie op te stellen met behulp van de Equation Editor maar krijg het helaas niet voor elkaar. Nu loop ik vast op het volgende vraagstuk:
Gegeven zijn de functies
[formule]Fp(x) = px^2 + (p+2)x + 3[/formule]
Bereken exact de waarden van p waarvoor
a)Fp een negatief minimum heeft
b)Fp een positief maximum heeft
Ik hoop dat de vraagstelling duidelijk is. Zover kom ik:
a) Negatief minimum voor p>0 (want dan dalparabool) en D>0
Tot hier volg ik het helemaal. Maar nu gebeurt er het volgende in de uitwerkingen: Op deze discriminant wordt de ABC-formule weer toegepast om de nulpunten van p te vinden. Oke, kan ik me nog in vinden. Echter, deze wordt weer als volgt genoteerd.
Vraag 1: Zou het toegestaan zijn om het zo te noteren? Ik zou namelijk wel inzien dat dit verwarrend is omdat we twee keer een discriminant benaderen.
Invullen van bovenstaande toegepaste ABC formule geeft:
Nu heb ik de twee snijpunten van de x-as.
Maarfijn, nu loop ik vast. Ik zou zeggen dat het antwoord onderstaand zou zijn:
Maar het antwoordenboek geeft:
Deze laatste begrijp ik alleen ťcht niet.
Ik hoop dat het enigszins duidelijk en overzichtelijk was, en dat iemand mij zou kunnen helpen. Tips over hoe de volgende keer beter een vraag te stellen natuurlijk ook altijd welkom!
Gegeven zijn de functies
[formule]Fp(x) = px^2 + (p+2)x + 3[/formule]
Bereken exact de waarden van p waarvoor
a)Fp een negatief minimum heeft
b)Fp een positief maximum heeft
Ik hoop dat de vraagstelling duidelijk is. Zover kom ik:
a) Negatief minimum voor p>0 (want dan dalparabool) en D>0
| 1 2 3 4 5 6 7 8 | D=b^2-4ac a = p b = p+2 c = 3 D = (p+2)(p+2)-4*p*3 D = p^2+4p+4- 12p D = p^2-8p+4 |
| 1 2 | D = b^2 - 4ac D = 64-16 = 48 |
Invullen van bovenstaande toegepaste ABC formule geeft:
| 1 | p = (64+sqrt{48})/2 v p = (64-sqrt{48})/2 |
Maarfijn, nu loop ik vast. Ik zou zeggen dat het antwoord onderstaand zou zijn:
| 1 | (64+sqrt{48})/2 < p < (64-sqrt{48})/2 |
| 1 | 0 < p < (64-sqrt{48})/2 v p > (64+sqrt{48})/2 |
Ik hoop dat het enigszins duidelijk en overzichtelijk was, en dat iemand mij zou kunnen helpen. Tips over hoe de volgende keer beter een vraag te stellen natuurlijk ook altijd welkom!


Wat je hier doet klopt niet, en de rest van je uitwerking dus ook niet. De discriminant is afhankelijk van p, en daarmee een functie van p. Maar hier doe jij opeens alsof de discriminant een constante waarde heeft, maar dit is de discriminant van de vierkantsvergelijking in p, en dat is wat anders. Je kunt een index p gebruiken om aan te geven dat de discriminant van je oorspronkelijke kwadratische veelterm afhangt van p, dusquote:Op zaterdag 8 februari 2014 13:34 schreef Maarten9191 het volgende:
Ik ga in mei een staatsexamen wiskunde B VWO doen waarin ik mij voorbereid d.m.v. de Getal en Ruimte reeks. Dit is mijn eerste post hier, en ik heb zo'n 10 minuten geprobeerd mijn functie op te stellen met behulp van de Equation Editor maar krijg het helaas niet voor elkaar. Nu loop ik vast op het volgende vraagstuk:
Gegeven zijn de functies
[formule]Fp(x) = px^2 + (p+2)x + 3[/formule]
Bereken exact de waarden van p waarvoor
a)Fp een negatief minimum heeft
b)Fp een positief maximum heeft
Ik hoop dat de vraagstelling duidelijk is. Zover kom ik:
a) Negatief minimum voor p>0 (want dan dalparabool) en D>0
[ code verwijderd ]
Tot hier volg ik het helemaal. Maar nu gebeurt er het volgende in de uitwerkingen: Op deze discriminant wordt de ABC-formule weer toegepast om de nulpunten van p te vinden. Oke, kan ik me nog in vinden. Echter, deze wordt weer als volgt genoteerd.
[ code verwijderd ]
Vraag 1: Zou het toegestaan zijn om het zo te noteren? Ik zou namelijk wel inzien dat dit verwarrend is omdat we twee keer een discriminant benaderen.
Dp = p2 − 8p + 4
Je bepaalt nu eerst de waarden van p waarvoor geldt Dp = 0, zodat je vervolgens een tekenschema kunt maken van Dp als functie van p. Je vindt dan dat Dp > 0 voor p < 4 − 2√3 ∨ p > 4 + 2√3.
Voor de eerste opgave zijn de voorwaarden p > 0 ∧ Dp > 0 en dat is het geval voor 0 < p < 4 − 2√3 ∨ p > 4 + 2√3.
Verder: gebruik geen code tags als je daar toch niets zinnigs mee doet, dit maakt het quoten van specifieke passages namelijk onnodig lastig. Gebruik Unicode of HTML entities of TeX.


Die tweede discriminant heb je helemaal niet nodig. (als in apart definiŽren)quote:Op zaterdag 8 februari 2014 13:34 schreef Maarten9191 het volgende:
Gegeven zijn de functies
[formule]Fp(x) = px^2 + (p+2)x + 3[/formule]
Bereken exact de waarden van p waarvoor
a)Fp een negatief minimum heeft
b)Fp een positief maximum heeft
Ik hoop dat de vraagstelling duidelijk is. Zover kom ik:
a) Negatief minimum voor p>0 (want dan dalparabool) en D>0
[ code verwijderd ]
Tot hier volg ik het helemaal. Maar nu gebeurt er het volgende in de uitwerkingen: Op deze discriminant wordt de ABC-formule weer toegepast om de nulpunten van p te vinden. Oke, kan ik me nog in vinden. Echter, deze wordt weer als volgt genoteerd.
[ code verwijderd ]
Vraag 1: Zou het toegestaan zijn om het zo te noteren? Ik zou namelijk wel inzien dat dit verwarrend is omdat we twee keer een discriminant benaderen.
Daarnaast als je alleen D opschrijft is het natuurlijk niet duidelijk.
Je mag echter ook Nederlands gebruiken.
En zoals Riparius zei een subscript gebruiken, of een totaal ander symbool. Als je maar duidelijk maakt wat het symbool is.
En dat antwoordenboek klopt volgens mij niet, tenzij 64/2 opeens gelijk is aan 4.


Riparius en t4rt4rus enorm bedankt voor jullie inbreng, het is me een stuk duidelijker geworden! Als ik nog ergens een keer mee zit weet ik waar ik moet zijn.
Dat 64/2 zal mijn fout zijn, geen idee hoe ik er bij kom, aangezien er in het boek gewoon 8 staat. Zal het om wat voor reden dan ook gekwadrateerd hebben. Afijn, erg bedankt
Dat 64/2 zal mijn fout zijn, geen idee hoe ik er bij kom, aangezien er in het boek gewoon 8 staat. Zal het om wat voor reden dan ook gekwadrateerd hebben. Afijn, erg bedankt


Ik denk eerder dat je nog met die 64 in je hoofd zat van je berekening van de discriminant van je vierkantsvergelijking in p. Maar, als ik je een tip mag geven: gebruik niet de abc-formule als dat niet echt nodig is. Je kunt die vierkantsvergelijking in p ook gemakkelijk oplossen via kwadraatafsplitsing, zodat je hier geen discriminant op had hoeven schrijven:quote:Op zaterdag 8 februari 2014 17:41 schreef Maarten9191 het volgende:
Riparius en t4rt4rus enorm bedankt voor jullie inbreng, het is me een stuk duidelijker geworden! Als ik nog ergens een keer mee zit weet ik waar ik moet zijn.
Dat 64/2 zal mijn fout zijn, geen idee hoe ik er bij kom, aangezien er in het boek gewoon 8 staat. Zal het om wat voor reden dan ook gekwadrateerd hebben. Afijn, erg bedankt
p2 − 8p + 4 = 0
(p − 4)2 − 16 + 4 = 0
(p − 4)2 = 12
p − 4 = 2√3 ∨ p − 4 = −2√3
p = 4 + 2√3 ∨ p = 4 − 2√3


Ik zie wat je doet ja, oogt een stuk sneller, eenvoudiger, en minder overzichtelijk. Ik zal er op letten, bedankt!


Ik hoop dat je bedoelt dat het juist overzichtelijker is ...quote:Op zaterdag 8 februari 2014 18:13 schreef Maarten9191 het volgende:
Ik zie wat je doet ja, oogt een stuk sneller, eenvoudiger, en minder overzichtelijk. Ik zal er op letten, bedankt!


Hallo allemaal.
Ik moet over een week een verslag voor natuurkunde inleven over twee vragen die zij heeft gesteld, Maar ik weet niet hoe ik dat allemaal moet berekenen.
Dit zijn de twee vragen die ik heb uitgevoerd:
1. Bepaling van de soortelijke warmte van een metaal.
Die 200 Ml water in de joulemeter (C = 60 J/ 'C). Roer 1 Min en meet daarna de begin- temperatuur. Breng een blokje metaal van 200 gram en 100 'C in de joulemeter. Roer totdat de temperatuur niet meer veranderd. Meet de eind- temperatuur.
Bereken de soortelijke warmte van het metaal. Zoek in de BINAS op welk metaal het is.
Water zonder metaal: 19 'C
Water met Metaal: 25 'C
2. Bepaling van de massa van een blokje ijzer.
Deo 200 Ml water in de joulemeter (C = 60 J/ 'C). Roer 1 Min en meet daarna de begin- temperatuur. Breng een blokje ijzen van 100 'C in de joulemeter. Roer totdat de temperatuur niet meer verandert. Meet de eind- temperatuur.
Bereken de massa van het blokje ijzer.
Water zonder ijzer: 19 'C
Water met ijzer: 29'C
Formules die we hebben gekregen:
(met * bedoel ik "keer")
Q = M * c * delta T
Q = C * delta T
Q op = Q af
Kan iemand met helpen met die berekening?
Ik moet over een week een verslag voor natuurkunde inleven over twee vragen die zij heeft gesteld, Maar ik weet niet hoe ik dat allemaal moet berekenen.
Dit zijn de twee vragen die ik heb uitgevoerd:
1. Bepaling van de soortelijke warmte van een metaal.
Die 200 Ml water in de joulemeter (C = 60 J/ 'C). Roer 1 Min en meet daarna de begin- temperatuur. Breng een blokje metaal van 200 gram en 100 'C in de joulemeter. Roer totdat de temperatuur niet meer veranderd. Meet de eind- temperatuur.
Bereken de soortelijke warmte van het metaal. Zoek in de BINAS op welk metaal het is.
Water zonder metaal: 19 'C
Water met Metaal: 25 'C
2. Bepaling van de massa van een blokje ijzer.
Deo 200 Ml water in de joulemeter (C = 60 J/ 'C). Roer 1 Min en meet daarna de begin- temperatuur. Breng een blokje ijzen van 100 'C in de joulemeter. Roer totdat de temperatuur niet meer verandert. Meet de eind- temperatuur.
Bereken de massa van het blokje ijzer.
Water zonder ijzer: 19 'C
Water met ijzer: 29'C
Formules die we hebben gekregen:
(met * bedoel ik "keer")
Q = M * c * delta T
Q = C * delta T
Q op = Q af
Kan iemand met helpen met die berekening?


Ja, maar ik doe het niet. Maak eerst maar eens een fatsoenlijke post en plaats die in het juiste topic, dus niet hier. Als je zoveel belachelijke typo's in je post laat staan, dan geef je impliciet al aan dat je er geen enkele moeite voor wenst te doen. Geef in je herziene post duidelijk aan wat je zelf al hebt geprobeerd en waarom je niet verder komt of waarom je denkt dat de verkregen uitkomsten niet kunnen kloppen.quote:Op maandag 10 februari 2014 18:47 schreef jelle321 het volgende:
Kan iemand met helpen met die berekening?


Hij stond ook al in het beta overige topic, alleen had meneer geen geduld.quote:Op maandag 10 februari 2014 19:59 schreef Riparius het volgende:
[..]
Ja, maar ik doe het niet. Maak eerst maar eens een fatsoenlijke post en plaats die in het juiste topic, dus niet hier. Als je zoveel belachelijke typo's in je post laat staan, dan geef je impliciet al aan dat je er geen enkele moeite voor wenst te doen. Geef in je herziene post duidelijk aan wat je zelf al hebt geprobeerd en waarom je niet verder komt of waarom je denkt dat de verkregen uitkomsten niet kunnen kloppen.


Analyse vraagje.
Opgave 4
Even wat notatie, die A met een streep is de kleinst mogelijke verzameling van A die gesloten is, d.w.z. de afsluiting van A. - A met een open rondje erboven is het inwendige van A. dA staat voor de rand van A.
Ik heb een 'bewijs' geschreven. In het kort laat ik zien dat z in 3 mogelijke deelverzamelingen van Rd kan zitten, en dat voor 2 deelverzamelingen geldt dat dist(z,A) = 0 en voor die andere laat ik zien dat die afstand altijd groter is dan 0. Op basis van die 3 zaken volgt dan de bewering.
Vooral bij de tweede deelverzameling dA weet ik niet zeker of dit bewijs wiskundig juist is. M.a.w. ik weet niet zeker hoe ik dat mathematisch juist opschrijf.. Iemand die daar iets over kan zeggen?
Hier mijn bewijs:
Misschien moet ik het anders verwoorden:
dist(z2, x~) < epsilon
=> dist(z2, x~) -> 0
moet ik opschrijven
| z2 - x~ | < epsilon
En omdat dist(z2, x~) het infimum van die verzameling is geldt:
dist(z2, x~) = 0?
[ Bericht 4% gewijzigd door #ANONIEM op 13-02-2014 00:13:53 ]
Opgave 4
Even wat notatie, die A met een streep is de kleinst mogelijke verzameling van A die gesloten is, d.w.z. de afsluiting van A. - A met een open rondje erboven is het inwendige van A. dA staat voor de rand van A.
Ik heb een 'bewijs' geschreven. In het kort laat ik zien dat z in 3 mogelijke deelverzamelingen van Rd kan zitten, en dat voor 2 deelverzamelingen geldt dat dist(z,A) = 0 en voor die andere laat ik zien dat die afstand altijd groter is dan 0. Op basis van die 3 zaken volgt dan de bewering.
Vooral bij de tweede deelverzameling dA weet ik niet zeker of dit bewijs wiskundig juist is. M.a.w. ik weet niet zeker hoe ik dat mathematisch juist opschrijf.. Iemand die daar iets over kan zeggen?
Hier mijn bewijs:
Misschien moet ik het anders verwoorden:
dist(z2, x~) < epsilon
=> dist(z2, x~) -> 0
moet ik opschrijven
| z2 - x~ | < epsilon
En omdat dist(z2, x~) het infimum van die verzameling is geldt:
dist(z2, x~) = 0?
[ Bericht 4% gewijzigd door #ANONIEM op 13-02-2014 00:13:53 ]


Dit kan echt veel simpeler door in plaats van dA de verzameling A' (verdichtingspunten van A) te beschouwen. Dat alles morgen.


Hey kan iemand me met bijvoorbeeld vraag 2c helpen :
Het antwoord op 2c is: -3
http://i57.tinypic.com/8wh24l.png
Het antwoord op 2c is: -3
http://i57.tinypic.com/8wh24l.png


Tip: kijk eens goed naar de grenzen van de integralen in de opdracht en dan naar die bij de vraag zelf.quote:Op dinsdag 18 februari 2014 10:51 schreef ronaldoo12 het volgende:
Hey kan iemand me met bijvoorbeeld vraag 2c helpen :
Het antwoord op 2c is: -3
http://i57.tinypic.com/8wh24l.png
~Si vis amari, ama~


nee sorry ik kom er niet uit.. misschien iets met 4-7 = -3 ?quote:Op dinsdag 18 februari 2014 11:00 schreef FedExpress het volgende:
[..]
Tip: kijk eens goed naar de grenzen van de integralen in de opdracht en dan naar die bij de vraag zelf.


Weet je wel wat een integraal voorstelt? Wat je daarmee uitrekent?quote:Op dinsdag 18 februari 2014 11:23 schreef ronaldoo12 het volgende:
[..]
nee sorry ik kom er niet uit.. misschien iets met 4-7 = -3 ?


De oppervlakte onder een grafiek, de grenzen geven de grenzen van de x-as waarbinnen de oppervlakte wordt uitgerekend.. de rest van de sommen vind ik verder prima te doen hoor.. alleen voor opgave 2 staat nergens echt duidelijk uitgelegd in t boek ..quote:Op dinsdag 18 februari 2014 11:24 schreef Viezze het volgende:
[..]
Weet je wel wat een integraal voorstelt? Wat je daarmee uitrekent?


Als je dat begrijpt is de som heel simpel. Je wil de oppervlakte weten op het interval 4,6 en je weet de oppervlaktes op de intervallen 1,4 en 1,6. De rest is heel simpel (en heb je hierboven ook al goed gegoktquote:Op dinsdag 18 februari 2014 11:29 schreef ronaldoo12 het volgende:
[..]
De oppervlakte onder een grafiek, de grenzen geven de grenzen van de x-as waarbinnen de oppervlakte wordt uitgerekend.. de rest van de sommen vind ik verder prima te doen hoor.. alleen voor opgave 2 staat nergens echt duidelijk uitgelegd in t boek ..


Aha dankjewel ! dan snap ik ze nu allemaal behalve 2e.. ik gok weer iets op 5*4 + 9 = 29 .. alleen t zou mij logisch lijken om dit te doen: 5+4 = 9quote:Op dinsdag 18 februari 2014 11:31 schreef Viezze het volgende:
[..]
Als je dat begrijpt is de som heel simpel. Je wil de oppervlakte weten op het interval 4,6 en je weet de oppervlaktes op de intervallen 1,4 en 1,6. De rest is heel simpel (en heb je hierboven ook al goed gegokt)




