SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Ik snap niet hoe je de voorwaarden van de absolute waarde moet schrijven
|x| = x als x>0 en x=0
|x| = -x als x<0 en x=0
en dit bijvoorbeeld toepassen op:
f(x) = |1 -(x +1)2|
Moet je eerst de nulpunten uitrekenen?
f(x) = 1 -(x +1)2 als 0≥ x≥ -2
En dan nog 2 voorwaardes voor x ≥ 0 en -2 ≥ x
Maar daar kom ik niet uit.
|1 -(x +1)2)| = 1 -(x +1)2 als 0≥ x≥ -2
|1 -(x +1)2)| = -(1 -(x +1)2) als x ≥ 0 en -2 ≥ x
Ok, volgens mij snap ik het al.
[ Bericht 8% gewijzigd door wiskundenoob op 09-11-2013 14:07:50 ]
|x| = x als x>0 en x=0
|x| = -x als x<0 en x=0
en dit bijvoorbeeld toepassen op:
f(x) = |1 -(x +1)2|
Moet je eerst de nulpunten uitrekenen?
f(x) = 1 -(x +1)2 als 0≥ x≥ -2
En dan nog 2 voorwaardes voor x ≥ 0 en -2 ≥ x
Maar daar kom ik niet uit.
|1 -(x +1)2)| = 1 -(x +1)2 als 0≥ x≥ -2
|1 -(x +1)2)| = -(1 -(x +1)2) als x ≥ 0 en -2 ≥ x
Ok, volgens mij snap ik het al.
[ Bericht 8% gewijzigd door wiskundenoob op 09-11-2013 14:07:50 ]
Nee het klopt niet. |x| = -x voor x < 0. Duidelijk snap je het nog niet helemaal.quote:Op zaterdag 9 november 2013 13:24 schreef wiskundenoob het volgende:
Ik snap niet hoe je de voorwaarden van de absolute waarde moet schrijven
|x| = x als x>0 en x=0
|x| = -x als x<0 en x=0
en dit bijvoorbeeld toepassen op:
f(x) = |1 -(x +1)2|
Moet je eerst de nulpunten uitrekenen?
f(x) = 1 -(x +1)2 als 0≥ x≥ -2
En dan nog 2 voorwaardes voor x ≥ 0 en -2 ≥ x
Maar daar kom ik niet uit.
|1 -(x +1)2)| = 1 -(x +1)2 als 0≥ x≥ -2
|1 -(x +1)2)| = -(1 -(x +1)2) als x ≥ 0 en -2 ≥ x
Ok, volgens mij snap ik het al.
Je zou dan ook kunnen beweren
f(x) = 1 voor x ≥ 0 en f(x) = -1 voor x ≤ 0
Dan f(0) = 1 en f(0) = -1 en dat kan niet, want dan is f geen functie.
[ Bericht 7% gewijzigd door #ANONIEM op 09-11-2013 14:14:50 ]
Jawel, de tweede voorwaarde is tegenovergestelde van de eerste voorwaarde. Heb het verkeerd opgeschreven.quote:
[..]
Nee het klopt niet. |x| = -x voor x < 0. Duidelijk snap je het nog niet helemaal.
Heb even wat toegevoegd. Dat het nu toevallig uitkomt zegt niet dat het mag.quote:
[..]
Jawel, de tweede voorwaarde is tegenovergestelde van de eerste voorwaarde. Heb het verkeerd opgeschreven.
Ok, geef een vergelijking dan probeer ik het op te lossen.quote:
[..]
Heb even wat toegevoegd. Dat het nu toevallig uitkomt zegt niet dat het mag.
Oke, misschien snap ik het toch niet? Als ik mijn antwoorden plot en de voorwaarden controleert dan klopt het gewoon?
Maar je voorwaarden kloppen niet.quote:Op zaterdag 9 november 2013 14:30 schreef wiskundenoob het volgende:
Oke, misschien snap ik het toch niet? Als ik mijn antwoorden plot en de voorwaarden controleert dan klopt het gewoon?
|x| = x voor x ≥ 0
|x| = -x voor x < 0 niet x ≤ 0
Je hebt −0 = 0 want (−1)·0 = 0, dus je mag ook zeggen dat |x| = −x voor x ≤ 0.quote:
[..]
Maar je voorwaarden kloppen niet.
|x| = x voor x ≥ 0
|x| = -x voor x < 0 niet x ≤ 0
Ik denk dat je vooral een notatieprobleem hebt. Het is gebruikelijk om functies die je niet met een eenduidig functievoorschrift weer kunt geven (althans: in jouw geval niet zonder absoluutstrepen te gebruiken) weer te geven met een accolade waarbij je de verschillende functievoorschriften met de bijbehorende voorwaarde voor de onafhankelijke variabele (meestal x) elk op een aparte regel achter de accolade zet. De benodigde TeX code om dit weer te geven werkt niet op FOK, dus dan maar even een plaatje als voorbeeld:quote:
Oke, misschien snap ik het toch niet? Als ik mijn antwoorden plot en de voorwaarden controleert dan klopt het gewoon?
Zie ook hier.
In principe wel, maar waarom zou je dat jezelf aanleren? Definieer subdomeinen niet dubbel in een functievoorschrift, klaar.quote:
[..]
Je hebt −0 = 0 want (−1)·0 = 0, dus je mag ook zeggen dat |x| = −x voor x ≤ 0.
Gewoon, omdat het juist is. Als je wordt gevraagd wat de verzameling is van alle reële waarden x waarvoor geldt |x| = −x, dan is het correcte antwoord { x ∈ R | x ≤ 0 } en niet { x ∈ R | x < 0 }.quote:
[..]
In principe wel, maar waarom zou je dat jezelf aanleren?
Dit is een goed advies, maar het staat los van het voorgaande.quote:Definieer subdomeinen niet dubbel in een functievoorschrift, klaar.
[ Bericht 0% gewijzigd door Riparius op 09-11-2013 19:26:35 ]
Oke, maar dat waren functies die ik moest schetsen.quote:
[..]
Ik denk dat je vooral een notatieprobleem hebt. Het is gebruikelijk om functies die je niet met een eenduidig functievoorschrift weer kunt geven (althans: in jouw geval niet zonder absoluutstrepen te gebruiken) weer te geven met een accolade waarbij je de verschillende functievoorschriften met de bijbehorende voorwaarde voor de onafhankelijke variabele (meestal x) elk op een aparte regel achter de accolade zet. De benodigde TeX code om dit weer te geven werkt niet op FOK, dus dan maar even een plaatje als voorbeeld:
[ afbeelding ]
Zie ook hier.
Waarvoor leer je al deze wiskunde eigenlijkquote:
[..]
Oke, maar dat waren functies die ik moest schetsen.
Gewoon niks te doen soms en dan maak ik wat opgaves in mijn boek.quote:
[..]
Waarvoor leer je al deze wiskunde eigenlijk
Maar het voorgaande staat los van het originele vraagstuk.quote:
[..]
Gewoon, omdat het juist is. Als je wordt gevraagd wat de verzameling is van alle reële waarden x waarvoor geldt |x| = −x, dan is het correcte antwoord { x ∈ R | x ≤ 0 } en niet { x ∈ R | x < 0 }.
[..]
Dit is een goed advies, maar het staat los van het voorgaande.
Maar ik begrijp je wel.
Het was daarom ook niet bedoeld op het originele vraagstuk, maar juist wat jij beweerdequote:Op zondag 10 november 2013 13:35 schreef Amoeba het volgende:
[..]
Maar het voorgaande staat los van het originele vraagstuk.
Maar ik begrijp je wel.
Waarom niet? Daar ging de vraag juist over.quote:Op zondag 10 november 2013 13:56 schreef tacos049 het volgende:
[..]
Het was daarom ook niet bedoeld op het originele vraagstuk, maar juist wat jij beweerde
Hmm, ja eigenlijk wel he.quote:
[..]
Waarom niet? Daar ging de vraag juist over.
Ik zou het meer interpreteren hoe je correct een (gebroken) functievoorschrift van |f(x)| opschreef. Maar in principe komt het erop neer om de verzameling reële getallen te bepalen waarvoor geldt |f(x)| = -f(x) en |f(x)| = f(x)
Maar dan nog kun je jezelf beter aanleren om in een functievoorschrift geen domeinen dubbel te definiëren, en dat is het punt wat ik al een tijdje probeer te maken.
[ Bericht 9% gewijzigd door #ANONIEM op 10-11-2013 15:21:06 ]
Wat gebeurt er met de coefficient of variance van arrivals en van de effective process times op 1 machine wanneer je onafhankelijke poisson arrivals hebt van twee producttypen(zelfde lamda) en poisson process tijden(producttype a-b ratio van 1:3)?
Met een simulatie in enterprise dynamics zou 1 van deze CV's 1,5 moeten worden ipv 1(bij een M/M/1 queue), maar waarom snap ik niet.
Met een simulatie in enterprise dynamics zou 1 van deze CV's 1,5 moeten worden ipv 1(bij een M/M/1 queue), maar waarom snap ik niet.
When I get sad, I stop being sad and just be awesome instead.
even een par simpele vragen,maar ik kan niet echt concreet antwoord vinden in mijn boek:
1)als je een parameter differentieert, bijv. ( f(x)= P x (X-2)2 -6),wordt het dan:
- F"(x)= P x 2X-4
- F"(x)= 1 x 2X-4
(ofwel, blijft de derde variabele bij een differentie staan of niet)
2) als je de inverse moet geven van: 3/(2x+4)
dan kom ik er wel op dat je dit moet doen:
x2 --> +4 --> 3/... en dan inversen: x/3 --> (x/3) +4--> ((x/3)+4) /2..
maar dan komt er zo'n inverse grafiek uit...kan iemand mij bevestiging geven of ik het goed heb gedaan?
1)als je een parameter differentieert, bijv. ( f(x)= P x (X-2)2 -6),wordt het dan:
- F"(x)= P x 2X-4
- F"(x)= 1 x 2X-4
(ofwel, blijft de derde variabele bij een differentie staan of niet)
2) als je de inverse moet geven van: 3/(2x+4)
dan kom ik er wel op dat je dit moet doen:
x2 --> +4 --> 3/... en dan inversen: x/3 --> (x/3) +4--> ((x/3)+4) /2..
maar dan komt er zo'n inverse grafiek uit...kan iemand mij bevestiging geven of ik het goed heb gedaan?
16-jarige gymnasiast met als hobby's wielrennen,gamen en muziek luisteren
Even een paar tips want zo is er geen touw aan vast te knopen en ga je geen hulp hier krijgen.
-Gebruik de benodigde sub, sup, en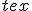
tags rond (delen van) je wiskundige uitdrukkingen om ze eenduidig en leesbaar neer te zetten.
-Speciale tekens (griekse letters, operatoren, enz.) kunnen ook met HTML en Unicode codes ingetikt worden. Googlen op mathematical symbols html of mathematical symbols unicode geeft al in eerste 10 hits voldoende bruikbare webpagina's.
-Gebruik de benodigde sub, sup, en
-Speciale tekens (griekse letters, operatoren, enz.) kunnen ook met HTML en Unicode codes ingetikt worden. Googlen op mathematical symbols html of mathematical symbols unicode geeft al in eerste 10 hits voldoende bruikbare webpagina's.
Je notatie is compleet hopeloos. Het kost mij meer tijd om je bericht te ontcijferen dan om je vragen te beantwoorden, en dat kan niet de bedoeling zijn. Gebruik om te beginnen nooit, maar dan ook helemaal nooit, de letter x als teken van vermenigvuldiging. Dit teken is ook geen x, maar een Andreaskruis × dat je op FOK kunt krijgen door & times; te typen zonder de spatie na de ampersand. Maar dan nog, gebruik liever de middle dot · die je krijgt door & middot; te typen zonder spatie na de &.quote:
Even een paar simpele vragen,maar ik kan niet echt concreet antwoord vinden in mijn boek:
Parameters differentieer je niet, je differentieert een functie die afhangt van een parameter. De parameter hangt hier niet af van je variabele x, en is dus een constante.quote:1) Als je een parameter differentieert ...
f(x) = p·(x−2)2 − 6
f'(x) = 2·p·(x − 2)
f''(x) = 2·p
Om een functie als deze te inverteren pas je elementaire algebraïsche regels toe die je als het goed is al jaren geleden hebt geleerd. De grafiek van de inverse van een functie krijg je door de grafiek te spiegelen in de lijn met vergelijking y = x, en aangezien hierbij een punt met coördinaten (x;y) overgaat in het punt met coördinaten (y;x) verkrijg je de vergelijking van de grafiek van de inverse functie door x en y om te wisselen. Vervolgens kun je dan proberen uit je nieuwe betrekking weer y op te lossen om zo een functievoorschrift te krijgen voor de inverse functie. Dat kan uiteraard alleen als de oorspronkelijke functie inverteerbaar is. Hier heb je danquote:2) Als je de inverse moet geven van: 3/(2x+4) ...
x = 3/(2y + 4)
x(2y + 4) = 3
2xy + 4x = 3
2xy = 3 − 4x
y = (3 − 4x)/2x
Je kunt het ook ietsje anders doen, als volgt
x = 3/(2y + 4)
2y + 4 = 3/x
2y = 3/x − 4
y = 3/(2x) − 2
sorry hiervoor,ik wist zo 1,2,3 niet hoe het moest,bedankt voor de uitleg daarvan, ik zal dat volgende keer zeker toepassenquote:Je notatie is compleet hopeloos. Het kost mij meer tijd om je bericht te ontcijferen dan om je vragen te beantwoorden, en dat kan niet de bedoeling zijn
voor de rest snap ik nu wel alle dingen die ik je vroeg,hartstikke bedankt:)
16-jarige gymnasiast met als hobby's wielrennen,gamen en muziek luisteren
Vraag 2009a, 6.
http://www.kaveurne.be/wiskunde/wiskunde.htm
Het antwoord moet hier D zijn.
We beschouwen een goniometrische vergelijking: sin²(2x)= 1/2
Hoeveel oplossingen voor deze vergelijking liggen tussen 0° en 360°
<A> 1
<B> 2
<C> 4
<D> 8
Ik had C, maar ik weet geloof ik waarom het D moet zijn. Als ik het m.b.v. algebra oplos kom ik op 4 antwoordmogelijkheden uit, echter deze bestaan tot 180 graden:
x= 23.5° + k * 180°
x= -23.5° + k * 180°
x= 67.5° + k * 180°
x= -67.5° + k * 180°
360 graden is het dubbele van 180 graden, dus het moet D zijn. Redeneer ik zo correct?
http://www.kaveurne.be/wiskunde/wiskunde.htm
Het antwoord moet hier D zijn.
We beschouwen een goniometrische vergelijking: sin²(2x)= 1/2
Hoeveel oplossingen voor deze vergelijking liggen tussen 0° en 360°
<A> 1
<B> 2
<C> 4
<D> 8
Ik had C, maar ik weet geloof ik waarom het D moet zijn. Als ik het m.b.v. algebra oplos kom ik op 4 antwoordmogelijkheden uit, echter deze bestaan tot 180 graden:
x= 23.5° + k * 180°
x= -23.5° + k * 180°
x= 67.5° + k * 180°
x= -67.5° + k * 180°
360 graden is het dubbele van 180 graden, dus het moet D zijn. Redeneer ik zo correct?
Het is niet nodig om de oplossingen expliciet te vinden. Ik zou persoonlijk even een cirkel tekenen. Als je dat doet zie je dat er voor sin(x)=y met y in (-1, 1) heb je twee oplossingen x in [0°,360°).quote:
Vraag 2009a, 6.
http://www.kaveurne.be/wiskunde/wiskunde.htm
Het antwoord moet hier D zijn.
We beschouwen een goniometrische vergelijking: sin²(2x)= 1/2
Hoeveel oplossingen voor deze vergelijking liggen tussen 0° en 360°
<A> 1
<B> 2
<C> 4
<D> 8
Ik had C, maar ik weet geloof ik waarom het D moet zijn. Als ik het m.b.v. algebra oplos kom ik op 4 antwoordmogelijkheden uit, echter deze bestaan tot 180 graden:
x= 23.5° + k * 180°
x= -23.5° + k * 180°
x= 67.5° + k * 180°
x= -67.5° + k * 180°
360 graden is het dubbele van 180 graden, dus het moet D zijn. Redeneer ik zo correct?
Omdat je nu hebt sin(x)2=y heb je al vier oplossingen, en omdat je niet sin(x), maar sin(2x) hebt, krijg je in totaal 8 oplossingen.
Dit is natuurlijk niet heel rigoureus (de redenering klopt bijvoorbeeld niet als y=0, want dan heb je door het kwadraat niet twee keer zoveel oplossingen), maar je begrijpt het idee
yupsquote:
Vraag 2009a, 6.
http://www.kaveurne.be/wiskunde/wiskunde.htm
Het antwoord moet hier D zijn.
We beschouwen een goniometrische vergelijking: sin²(2x)= 1/2
Hoeveel oplossingen voor deze vergelijking liggen tussen 0° en 360°
<A> 1
<B> 2
<C> 4
<D> 8
Ik had C, maar ik weet geloof ik waarom het D moet zijn. Als ik het m.b.v. algebra oplos kom ik op 4 antwoordmogelijkheden uit, echter deze bestaan tot 180 graden:
x= 23.5° + k * 180°
x= -23.5° + k * 180°
x= 67.5° + k * 180°
x= -67.5° + k * 180°
360 graden is het dubbele van 180 graden, dus het moet D zijn. Redeneer ik zo correct?
afgezien van die 23,5 deg waar Riparius even hieronder terecht op wijst want 45/2 = 22,5 sin2(2x) = 1/2
sin(2x) = ½√2 ∨ -½√2
sin(2x) = sin(¼π) ∨ sin(-¼π)
2x = ¼π+2kπ ∨ π-¼π+2kπ ∨ -¼π+2kπ ∨ π+¼π+2kπ
2x = ¼π+2kπ ∨ ¾π+2kπ ∨ 1¾π+2kπ ∨ 1¼π+2kπ
x = ⅛π+kπ ∨ ⅜π+kπ ∨ ⅞π+kπ ∨ ⅝π+kπ
Dat zijn 4 oplossingen in 1 periode van pi, dus in 2pi worden dat er dus 8 in totaal.
PS: als je de breuken niet goed genoeg kan zien even 1 of 2 keer CTRL+"+" drukken om op de tekst in te zoomen, en CRTL+"-" om terug uit te zoomen.
[ Bericht 2% gewijzigd door VanishedEntity op 11-11-2013 20:27:32 ]
Dit is niet correct geredeneerd. Bestudeer de uitwerking van de oplosser van Veurne. De helft van 45° is 22,5°, niet 23,5°. Verder geef je hier niet de juiste hoeken na elkaar. Bij de sinus is het zo dat supplementaire (rotatie)hoeken dezelfde sinus hebben, maar jij lijkt hier te veronderstellen dat tegengestelde (rotatie)hoeken dezelfde sinus hebben, en dat is niet zo. Tegengestelde rotatiehoeken hebben ook tegengestelde sinussen (maar wel dezelfde cosinus).quote:
Vraag 2009a, 6.
http://www.kaveurne.be/wiskunde/wiskunde.htm
Het antwoord moet hier D zijn.
We beschouwen een goniometrische vergelijking: sin²(2x)= 1/2
Hoeveel oplossingen voor deze vergelijking liggen tussen 0° en 360°
<A> 1
<B> 2
<C> 4
<D> 8
Ik had C, maar ik weet geloof ik waarom het D moet zijn. Als ik het m.b.v. algebra oplos kom ik op 4 antwoordmogelijkheden uit, echter deze bestaan tot 180 graden:
x= 23.5° + k * 180°
x= -23.5° + k * 180°
x= 67.5° + k * 180°
x= -67.5° + k * 180°
360 graden is het dubbele van 180 graden, dus het moet D zijn. Redeneer ik zo correct?
Je kunt het hier weer veel eenvoudiger doen dan wat de oplosser van Veurne doet als je gebruik maakt van het procédé dat bekend staat als overgaan op de dubbele hoek (zie het boekje van Van der Linden, p. 59).
We hebben de volgende identiteit
cos 2α = 1 − 2·sin2α
We kunnen hieruit sin2α vrijmaken, en dan krijgen we
sin2α = ½ − ½·cos 2α
Kiezen we nu α = 2x, dan is 2α = 4x en hebben we dus de volgende identiteit
sin22x = ½ − ½·cos 4x
De vergelijking
sin22x = ½
is dus ook te schrijven als
½ − ½·cos 4x = ½
en dus
cos 4x = 0
Nu is de cosinus nul in de punten (0; 1) en (0; −1) op de eenheidscirkel, en deze punten worden bereikt door het startpunt (1; 0) rond de oorsprong te roteren over een hoek van 90° plus of min een geheel aantal halve slagen, zodat we krijgen
4x = 90° + k·180°, k ∈ Z
en dus
x = 22,5° + k·45°, k ∈ Z
Je ziet nu direct dat je k = 0 .. 7 kunt nemen om een (rotatie)hoek te verkrijgen tussen 0 en 360°, zodat het juiste antwoord inderdaad <D> 8 is.
[ Bericht 0% gewijzigd door Riparius op 11-11-2013 21:57:48 ]
Nitpicking, maar wel terecht.quote:
Dit is niet correct geredeneerd. De helft van 45° is 22,5°, niet 23,5°.
Daar ligt het probleem niet; de fout, voor zover je het een fout kan noemen, die DefinitionX daar heeft gemaakt is dat hij de negatieve oplossingen niet dusdanig verschoven heeft, dat ze binnen dezelfde periode, die van 0 tot pi loopt, waarin ook de positieve oplossingen zitten, komen te liggen. Doordat de sinus in de oorspronkelijke opgave gekwadrateerd is, heb je hier met zowel positieve als negatieve oplossingen te maken, en zowel de positieve oplossing als de negatieve oplossing komt in de vorm van een paar, nl. arg + 2kπ, én π-arg + 2kπ. Je ziet dit mooi in mijn oplossingsstrategie; de derde oplossing op lijn 4 ligt niet binnen 0 en 2π, maar door 2π erbij op te tellen krijg ik uiteindelijk 1¾pi wat wel daarbinnen ligt. Als we vervolgens alle 4 gevonden oplossingen ( ¼π; ¾π; (5/4)π; (7/4)π) delen door 2, krijgen we uiteindelijk alle 4 de antwoorden binnen een periode van 0 tot π .quote:Verder neem je hier niet de juiste hoeken. Bij de sinus is het zo dat supplementaire (rotatie)hoeken dezelfde sinus hebben, maar jij lijkt hier te veronderstellen dat tegengestelde (rotatie)hoeken dezelfde sinus heben, en dat is niet zo. Tegengestelde rotatiehoeken hebben ook tegengestelde sinussen (maar wel dezelfde cosinus).
Vergelijken we dit met de antwoorden van DefinitionX, dan zien we dat door de negatieve antwoorden van DefinitionX met π oftewel 180° op te schuiven we op idd 22,5° <=> (1/4)π, 67,5° <=> (3/4)π, 122,5° <=> (5/4)π, en 157,5° <=> (7/4)π uitkomen.
Niet nodig zoals je even hierboven kunt zien. 6 regels en klaarquote:Je kunt het hier weer veel eenvoudiger doen dan wat de oplosser van Veurne doet als je gebruik maakt van het procédé dat bekend staat als overgaan op de dubbele hoek (zie het boekje van Van der Linden, p. 59).
Nee, dat is niet waar ik op doelde. DefinitionX zegt dat hij de vergelijking 'algebraïsch' heeft opgelost. Daarmee bedoelt hij hoogstwaarschijnlijk datquote:
Daar ligt het probleem niet; de fout, voor zover je het een fout kan noemen, die DefinitionX daar heeft gemaakt is dat hij de negatieve oplossingen niet dusdanig verschoven heeft, dat ze binnen dezelfde periode, die van 0 tot pi loopt, waarin ook de positieve oplossingen zitten, komen te liggen.
[..]
sin22x = ½
equivalent is met
sin 2x = ½√2 ∨ sin 2x = −½√2
Voor de eerste vergelijking hebben we dan
x = 22,5° + k·180° ∨ x = 67,5° + k·180°, k ∈ Z
en voor de tweede vergelijking
x = −22,5° + k·180° ∨ x = −67,5° + k·180°, k ∈ Z
Maar als je nu kijkt naar de volgorde waarin DefinitionX deze vier mogelijkheden opschrijft, dan zie je dat hij (afgezien van zijn rekenfout) eerst x = 22,5° + k·180° en x = −22,5° + k·180° geeft en dan x = 67,5° + k·180° en x = −67,5° + k·180°. Dit verraadt dat hij is uitgegaan van de onjuiste veronderstelling dat tegengestelde (rotatie)hoeken dezelfde sinus hebben. Het komt hier inderdaad goed uit, maar de onderliggende redenatie blijft gewoon fout.
Overgaan op de dubbele hoek is een beproefde techniek die vroeger in Nederland ook op school werd geleerd, en in Vlaanderen is dat nog steeds zo. Er komen in die Vlaamse toelatingsexamens vaak goniometrische vergelijkingen voor met een kwadraat van een sinus of een cosinus, en dan is het uitermate zinnig om te weten dat je deze kwadraten kunt herschrijven met behulp van een cosinus van de dubbele hoek:quote:Niet nodig zoals je even hierboven kunt zien. 6 regels en klaar
cos2α = ½(1 + cos 2α)
sin2α = ½(1 − cos 2α)
De oplossing wordt dan toch stukken eenvoudiger:
sin22x = ½
cos 4x = 0
x = 22,5° + k·45°, k ∈ Z
De identiteiten voor de herleiding van het kwadraat van een cosinus of een sinus tot de cosinus van de dubbele hoek worden ook vaak gebruikt in de integraalrekening, en ook daarover kunnen opgaven voorkomen bij de Vlaamse toelatingsexamens.
[ Bericht 0% gewijzigd door Riparius op 11-11-2013 21:34:52 ]
Nee, die conclusie kan je uit zijn twee antwoordenparen niet trekken, dat is te voorbarig becommentarieerd van jou!! Het klopt idd dat tegengestelde (rotatie)hoeken een tegengestelde sinus hebben, maar als men twee tegengestelde sinuswaarden elk afzonderlijk kwadrateert, blijken zowel de positieve sinus als de negatieve sinus beide dezelfde oplossing te geven. Dit is geen toevalligheid, maar volgt direct uit de eigenschap van 2 oplossingen voor even machten. Daar maak ik hier gebruik van. Bovendien, die -1/8pi en -3/8pi zijn op te vatten als de 5/8pi en 7/8pi van de vorige periode/golf, en je weet dat het antwoord niet verandert wanneer je een periode opschuift.quote:
Nee, dat is niet waar ik op doelde. DefinitionX zegt dat hij de vergelijking 'algebraïsch' heeft opgelost. Daarmee bedoelt hij hoogstwaarschijnlijk dat
sin22x = ½
equivalent is met
sin 2x = ½√2 ∨ sin 2x = −½√2
Voor de eerste vergelijking hebben we dan
x = 22,5° + k·180° ∨ x = 67,5° + k·180°, k ∈ Z
en voor de tweede vergelijking
x = −22,5° + k·180° ∨ x = −67,5° + k·180°, k ∈ Z
Maar als je nu kijkt naar de volgorde waarin DefinitionX deze vier mogelijkheden opschrijft, dan zie je dat hij (afgezien van zijn rekenfout) eerst x = 22,5° + k·180° en x = −22,5° + k·180° geeft en dan x = 67,5° + k·180° en x = −67,5° + k·180°. Dit verraadt dat hij is uitgegaan van de onjuiste veronderstelling dat tegengestelde (rotatie)hoeken dezelfde sinus hebben. Het komt hier inderdaad goed uit, maar de onderliggende redenatie blijft gewoon fout.
Dat neemt niet weg dat strikt genomen dat stuk gonio niet nodig is geweest om dit vraagstuk tot een goed einde brengen.quote:Overgaan op de dubbele hoek is een beproefde techniek die vroeger in Nederland ook op school werd geleerd, en in Vlaanderen is dat nog steeds zo. Er komen in die Vlaamse toelatingsexamens vaak goniometrische vergelijkingen voor met een kwadraat van een sinus of een cosinus, en dan is het uitermate zinnig om te weten dat je deze kwadraten kunt herschrijven met behulp van een cosinus van de dubbele hoek:
cos2a = ½(1 + cos 2α)
sin2a = ½(1 − cos 2α)
De oplossing wordt dan toch stukken eenvoudiger:
sin22x = ½
cos 4x = 0
x = 22,5° + k·45°, k ∈ Z
De identiteiten voor de herleiding van het kwadraat van een cosinus of een sinus tot de cosinus van de dubbele hoek worden ook vaak gebruikt in de integraalrekening, en ook daarover kunnen opgaven voorkomen bij de Vlaamse toelatingsexamens.
Bepaal alle complexe getallen z, met Re(z^2)=Im(z^2).
Ik dacht laat z=a+bi dan Re(z^2)=a^2-b^2 en Im(z^2)=2ab en dan oplossen a^2-b^2=2ab, maar dat lukt me niet echt. Iemand een ander idee?
Ik dacht laat z=a+bi dan Re(z^2)=a^2-b^2 en Im(z^2)=2ab en dan oplossen a^2-b^2=2ab, maar dat lukt me niet echt. Iemand een ander idee?
Kijk, als je nou je merkwaardige producten kende en vroeger had geleerd om kwadraten af te splitsen, dan deed je gewoon dit:quote:
Bepaal alle complexe getallen z, met Re(z^2)=Im(z^2).
Ik dacht laat z=a+bi dan Re(z^2)=a^2-b^2 en Im(z^2)=2ab en dan oplossen a^2-b^2=2ab, maar dat lukt me niet echt. Iemand een ander idee?
a2 − b2 − 2ab = 0
(a − b)2 − 2b2 = 0
(a − b − √2·b)(a − b + √2·b) = 0
a = (1 + √2)b ∨ a = (1 − √2)b
Re(z) = (1 + √2)·Im(z) ∨ Re(z) = (1 − √2)·Im(z)
Dus als ik het goed heb is de verzameling van alle z die daaraan voldoet: v = {z=(1+sqrt(2))x+xi of z=(1-sqrt(2))x+xi met x element van de reële getallen} ?quote:
[..]
Kijk, als je nou je merkwaardige producten kende en vroeger had geleerd om kwadraten af te splitsen, dan deed je gewoon dit:
a2 − b2 − 2ab = 0
(a − b)2 − 2b2 = 0
(a − b − √2·b)(a − b + √2·b) = 0
a = (1 + √2)b ∨ a = (1 − √2)b
Re(z) = (1 + √2)·Im(z) ∨ Re(z) = (1 − √2)·Im(z)
V = { z ∈ C | (z = (1 + √2)x + xi ∨ z = (1 − √2)x + xi) ∧ x ∈ R }quote:
[..]
Dus als ik het goed heb is de verzameling van alle z die daaraan voldoet: v = {z=(1+sqrt(2))x+xi of z=(1-sqrt(2))x+xi met x element van de reële getallen} ?
De beeldpunten van deze complexe getallen vormen in het complexe vlak twee rechte lijnen die elkaar loodrecht snijden in de oorsprong.
Als je een lijn vanuit het midden van een hoek tekent, hoe heet die lijn dan ook al weer? 
Dus je hebt bijvoorbeeld een hoek van 90 graden ten opzichte van lijn a en de lijn teken je dan op een hoek van 45 graden ten opzichte van lijn a.
Dus je hebt bijvoorbeeld een hoek van 90 graden ten opzichte van lijn a en de lijn teken je dan op een hoek van 45 graden ten opzichte van lijn a.
Gist is liefde, gist is leven. Vooral in een vagijn.
Bissectricequote:
Als je een lijn vanuit het midden van een hoek tekent, hoe heet die lijn dan ook al weer?
Ik heb een kopie van een stuk van een CD, 1 op 1, en moet de straal van de CD bepalen daarmee. Nu is me dat al gelukt door twee raaklijnen te tekenen en dan loodrecht daarop lijnen te tekenen, die lijnen te laten kruisen, en dan gewoon te meten. Maar de docent zei dat ik er ook een formule was. Met wat googelen kan ik eigenlijk niet veel vinden, kom vaak terecht op formules om de omtrek van de cirkel te bepalen aan de hand van de straal. Iemand een idee?
Gist is liefde, gist is leven. Vooral in een vagijn.
Daar heb ik te weinig gegevens voor.quote:
Iets met dit?
x2 +y2 + ax +by +c =0
Gist is liefde, gist is leven. Vooral in een vagijn.
Bedoel je nu dat je het middelpunt van een deel van een cirkel wil bepalen, en daarmee de straal?quote:
Ik heb een kopie van een stuk van een CD, 1 op 1, en moet de straal van de CD bepalen daarmee. Nu is me dat al gelukt door twee raaklijnen te tekenen en dan loodrecht daarop lijnen te tekenen, die lijnen te laten kruisen, en dan gewoon te meten. Maar de docent zei dat ik er ook een formule was. Met wat googelen kan ik eigenlijk niet veel vinden, kom vaak terecht op formules om de omtrek van de cirkel te bepalen aan de hand van de straal. Iemand een idee?
Misschien wat analytische meetkunde: kies drie punten op het cirkelsegment. Geef deze coördinaten. Laat deze een driehoek vormen. Stel vergelijkingen voor de middelloodlijnen van twee zijdes van die driehoek op. Die snijden elkaar in het middelpunt (want de middelloodlijnen van een driehoek snijden elkaar in het middelpunt van de omgeschreven cirkel; dit gebruik je andersom). Afstand van het bepaalde middelpunt tot één van de drie gekozen punten bepalen (Pythagoras) en je hebt de straal.
Of denk ik te moeilijk? Bedoelt de docent iets anders?
Dat met de loodlijnen heb ik dus al gedaan. En hij zei dat we die formule moesten opzoeken, dus denk niet dat het de stelling van Pythagoras is.quote:
[..]
Bedoel je nu dat je het middelpunt van een deel van een cirkel wil bepalen, en daarmee de straal?
Misschien wat analytische meetkunde: kies drie punten op het cirkelsegment. Geef deze coördinaten. Laat deze een driehoek vormen. Stel vergelijkingen voor de middelloodlijnen van twee zijdes van die driehoek op. Die snijden elkaar in het middelpunt (want de middelloodlijnen van een driehoek snijden elkaar in het middelpunt van de omgeschreven cirkel; dit gebruik je andersom). Afstand van het bepaalde middelpunt tot één van de drie gekozen punten bepalen (Pythagoras) en je hebt de straal.
Of denk ik te moeilijk? Bedoelt de docent iets anders?
Gist is liefde, gist is leven. Vooral in een vagijn.
Zo'n stuk heb ik dus, en dan moet ik de straal bepalen op twee manieren. Dit is het enige wat de docent er over zegt:
quote:Voor de berekening van de straal moet je ook zelf op zoek naar een formule. Afleiden is niet nodig, maar geef wel aan wat de formule is die je gebruikt hebt en waar die vandaan komt (bronvermelding!).
Gist is liefde, gist is leven. Vooral in een vagijn.
Pythagoras is helemaal niet de kern van mijn idee. Het is een stukje analytische meetkunde (dus met formules). Je kiest drie punten op de cirkel, je geeft die coördinaten en de rest van je oplossing komt neer op dat het snijpunt van de middelloodlijnen van een driehoek het middelpunt van de omgeschreven cirkel is. Dat is iets heel anders dan raaklijnen tekenen en daar lijnen loodrecht op nemen.quote:
[..]
Dat met de loodlijnen heb ik dus al gedaan. En hij zei dat we die formule moesten opzoeken, dus denk niet dat het de stelling van Pythagoras is.
Het rechte stuk is een koorde van de cirkel gevormd door de omtrek van de CD. Noem de straal van de cirkel r en de halve middelpuntshoek die door de koorde wordt omspannen α, dan is de lengte van de koorde 2·r·sin α en de afstand van het midden van de koorde tot de cirkel r·(1 − cos α). Het quotiënt van deze lengtes is danquote:
[ afbeelding ]
Zo'n stuk heb ik dus, en dan moet ik de straal bepalen op twee manieren. Dit is het enige wat de docent er over zegt:
[..]
r·(1 − cos α) / 2·r·sin α = ½·tan ½α
aangezien
tan ½α = (1 − cos α)/sin α
zodat je tan ½α en daarmee α kunt bepalen (0 < α < ½π). Zodoende ken je ook sin α en cos α en kun je dus r berekenen uit de opgemeten lengte 2·r·sin α van de koorde.
Ik had de formule net gevonden in mijn boek, en toen las ik je post, toevallig allemaal.quote:
[..]
Het rechte stuk is een koorde van de cirkel gevormd door de omtrek van de CD. Noem de straal van de cirkel r en de halve middelpuntshoek die door de koorde wordt omspannen α, dan is de lengte van de koorde 2·r·sin α en de afstand van het midden van de koorde tot de cirkel r·(1 − cos α). Het quotiënt van deze lengtes is dan
r·(1 − cos α) / 2·r·sin α = ½·tan ½α
aangezien
tan ½α = (1 − cos α)/sin α
zodat je tan ½α en daarmee α kunt bepalen (0 < α < ½π). Zodoende ken je ook sin α en cos α en kun je dus r berekenen uit de opgemeten lengte 2·r·sin α van de koorde.
In ieder geval bedankt. 
Gist is liefde, gist is leven. Vooral in een vagijn.
Het kan natuurlijk ook met Pythagoras, en dat is misschien hier wel zo makkelijk.quote:Op donderdag 14 november 2013 21:08 schreef Rezania het volgende:
[..]
Ik had de formule net gevonden in mijn boek, en toen las ik je post, toevallig allemaal.
Noem de lengte van de koorde k en de afstand van het midden van de koorde tot de cirkel p, en de gezochte straal R, dan hebben we volgens Pythagoras
(½k)2 + (R − p)2 = R2
Uitwerken geeft
¼k2 + R2 − 2Rp + p2 = R2
¼k2 − 2Rp + p2 = 0
2pR = ¼k2 + p2
Ja, die is wel een stuk makkelijker inderdaad, vooral met het plaatje. Ik gebruik die wel.quote:
[..]
Het kan natuurlijk ook met Pythagoras, en dat is misschien hier wel zo makkelijk.
[ afbeelding ]
Noem de lengte van de koorde k en de afstand van het midden van de koorde tot de cirkel p, en de gezochte straal R, dan hebben we volgens Pythagoras
(½k)2 + (R − p)2 = R2
Uitwerken geeft
¼k2 + R2 − 2Rp + p2 = R2
¼k2 − 2Rp + p2 = 0
2pR = ¼k2 + p2
[ afbeelding ]
Hoe vind je zoiets iets eigenlijk, dat plaatje bedoel ik? Heeft het een specifieke naam, zoek je op specifieke termen, of maak je het gewoon zelf? Want ik probeerde eerst te zoeken op internet, maar daar kwam ik niet heel ver mee. Misschien ook wel doordat ik zocht op "omtrek cirkel straal berekenen".
Gist is liefde, gist is leven. Vooral in een vagijn.
Je probleem was kennelijk dat je niet wist hoe z'n stuk van een cirkelschijf heet. Welnu, zo'n stuk noemen we een cirkelsegment.quote:
[..]
Ja, die is wel een stuk makkelijker inderdaad, vooral met het plaatje. Ik gebruik die wel.
Hoe vind je zoiets iets eigenlijk, dat plaatje bedoel ik? Heeft het een specifieke naam, zoek je op specifieke termen, of maak je het gewoon zelf? Want ik probeerde eerst te zoeken op internet, maar daar kwam ik niet heel ver mee. Misschien ook wel doordat ik zocht op "omtrek cirkel straal berekenen".
Oh mijn god, zo simpel.quote:
[..]
Je probleem was kennelijk dat je niet wist hoe z'n stuk van een cirkelschijf heet. Welnu, zo'n stuk noemen we een cirkelsegment.
Gist is liefde, gist is leven. Vooral in een vagijn.
