SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Ah. Ik ben niet zoveel naar college geweestquote:Op zondag 13 januari 2013 16:15 schreef Tochjo het volgende:
In het Nederlands heet zo'n ding een ondergroep.
Op internet ben ik de term deelgroep geloof ik wel eens tegen gekomen, vind ik ook eigenlijk logischer
Met convolutie product maakt 't niks uit of je f(t) verwisselt met g(t)?
Alleen de weg ernaartoe gaat er anders uitzien, true story?
Like 3 x 4 = 12 en 4 x 3 = ook 12
Alleen de weg ernaartoe gaat er anders uitzien, true story?
Like 3 x 4 = 12 en 4 x 3 = ook 12
Blues ain't nothing but a good man feeling bad...
Dat kan je natuurlijk ook zelf checken door naar de definitie van een convolutieproduct te kijken.quote:
Met convolutie product maakt 't niks uit of je f(t) verwisselt met g(t)?
Alleen de weg ernaartoe gaat er anders uitzien, true story?
Like 3 x 4 = 12 en 4 x 3 = ook 12
Wat studeer je eigenlijk?
Commutativiteit is een mooi woord ervoor (nu kan je het naast zelf uitwerken en vragen ook googlenquote:
Met convolutie product maakt 't niks uit of je f(t) verwisselt met g(t)?
Alleen de weg ernaartoe gaat er anders uitzien, true story?
Like 3 x 4 = 12 en 4 x 3 = ook 12
)
Aviation Engineering, jullie zijn veel leuker dan google
Blues ain't nothing but a good man feeling bad...
Even een simpele (schoonheids)vraagje over een F-distributie tabel. Ik heb 2 cijfers v1 149 en v2 149. Moet ik dan via het tabel naar boven of naar beneden afronden? Dus 140,140 of 160,160. Ik zou zeggen 140,140 maar bij sommige dingen moet je het altijd naar boven afronden. Vandaar dat ik het zeker wil weten.
Logaritme vraag:
T uitdrukken in R
R = 2 - 3LOG(t^2)
Stap 1 volgens antwoordenboek: 3LOG(t^2) = 2 - R.
Waarom is dit 2 - R en niet R - 2?
T uitdrukken in R
R = 2 - 3LOG(t^2)
Stap 1 volgens antwoordenboek: 3LOG(t^2) = 2 - R.
Waarom is dit 2 - R en niet R - 2?
A wat kijk jij scheve kaasblok
Je haalt 2 naar links (ofwel, haal van beide kanten 2 af). Dit geeft:quote:
Logaritme vraag:
T uitdrukken in R
R = 2 - 3LOG(t^2)
Stap 1 volgens antwoordenboek: 3LOG(t^2) = 2 - R.
Waarom is dit 2 - R en niet R - 2?
R-2 = -3LOG(t^2)
Vermenig nu beide kanten met -1. Dit geeft:
-R+2 = 3LOG(t^2)
Ofwel:
R+2 = 3LOG(t^2)
26"
Fading slowly.
Fading slowly.
Sorry dat ik je hier mee lastig val maar als ik dit zo lees, kom jij uit op R+2. Terwijl het antwoordenboek zegt 2-R. Is dit een fout in het antwoordenboek? Nogmaals excuses.quote:Op maandag 14 januari 2013 19:55 schreef Unsub het volgende:
[..]
Je haalt 2 naar links (ofwel, haal van beide kanten 2 af). Dit geeft:
R-2 = -3LOG(t^2)
Vermenig nu beide kanten met -1. Dit geeft:
-R+2 = 3LOG(t^2)
Ofwel:
R+2 = 3LOG(t^2)
A wat kijk jij scheve kaasblok
Sorry, ik ben slordigquote:
[..]
Sorry dat ik je hier mee lastig val maar als ik dit zo lees, kom jij uit op R+2. Terwijl het antwoordenboek zegt 2-R. Is dit een fout in het antwoordenboek? Nogmaals excuses.
Het moet natuurlijk zijn:
Je haalt 2 naar links (ofwel, haal van beide kanten 2 af). Dit geeft:
R-2 = -3LOG(t^2)
Vermenig nu beide kanten met -1. Dit geeft:
-R+2 = 3LOG(t^2)
Ofwel:
2-R = 3LOG(t^2)
26"
Fading slowly.
Fading slowly.
Ik kom niet verder bij deze opgave:
Bepaal van de volgende 3 idealen of het priem is in respectievelijk![\mathbb{Z}[X],\mathbb{Q}[X],\mathbb{F_2}[X]](https://forum.fok.nl/lib/mimetex.cgi?%20%5Cmathbb%7BZ%7D%5BX%5D%2C%5Cmathbb%7BQ%7D%5BX%5D%2C%5Cmathbb%7BF_2%7D%5BX%5D%20%20)
1: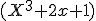
2: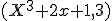
3: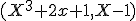
De eerste lukt wel: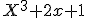
is irreducibel in ![\mathbb{Z}[X],\mathbb{Q}[X]](https://forum.fok.nl/lib/mimetex.cgi?%20%5Cmathbb%7BZ%7D%5BX%5D%2C%5Cmathbb%7BQ%7D%5BX%5D%20)
en reducibel in ![\mathbb{F_2}[X]](https://forum.fok.nl/lib/mimetex.cgi?%20%5Cmathbb%7BF_2%7D%5BX%5D%20%20)
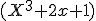, en dus is een priemideaal in en niet in
Hoe pak ik nu de tweede aan?
Bepaal van de volgende 3 idealen of het priem is in respectievelijk
1:
2:
3:
De eerste lukt wel:
Hoe pak ik nu de tweede aan?
Gebruik deze stelling:quote:
Ik kom niet verder bij deze opgave:
Bepaal van de volgende 3 idealen of het priem is in respectievelijk
1:
2:
3:
De eerste lukt wel:
Hoe pak ik nu de tweede aan?
An ideal I in the ring R (with unity) is prime if and only if the factor ring R/I is an integral domain.
Voor de rest gaat niemand je huiswerk maken, want ringtheorie is niet makkelijk.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Het element 3 is inverteerbaar in zowel Q als F2, dus daar heb je in geval 2 het eenheidsideaal te pakken. Voor Z[x] moet je bedenken dat Z[x]/(x^3+2x+1,3) isomorf is met F3[x]/(x^3+2x+1), dus gaat het erom of x^3 + 2x + 1 irreducibel is over F3.quote:
Ik kom niet verder bij deze opgave:
Bepaal van de volgende 3 idealen of het priem is in respectievelijk
1:
2:
3:
De eerste lukt wel:
Hoe pak ik nu de tweede aan?
Ik ben met reeksen en limieten bezig maar ik snap niet wat het antwoord op deze moet zijn:
limiet voor n naar oneindig (3+2^n)/(3^(n+2))
Ik pak het zo aan:
Eerst opsplitsen 3/(3^n*3^2) + 2^n/(3^n*3^2)
Dan de constanten naar voren: 3/9 * 1/3^n + 1/9 * 2^n/3^n
Dan machten naar boven: (1/3)^n + (2/3)^n.
Die zijn hetzelfde als 1/(1-x).
Dan kom je op: 3/9 * 3/2 + 1/9 * 3/1 = 5/6de uit.
Echter wolfram komt op 0 uit en een andere limieten bereken website op 4/9de.
Wat doe ik fout?
limiet voor n naar oneindig (3+2^n)/(3^(n+2))
Ik pak het zo aan:
Eerst opsplitsen 3/(3^n*3^2) + 2^n/(3^n*3^2)
Dan de constanten naar voren: 3/9 * 1/3^n + 1/9 * 2^n/3^n
Dan machten naar boven: (1/3)^n + (2/3)^n.
Die zijn hetzelfde als 1/(1-x).
Dan kom je op: 3/9 * 3/2 + 1/9 * 3/1 = 5/6de uit.
Echter wolfram komt op 0 uit en een andere limieten bereken website op 4/9de.
Wat doe ik fout?
When I get sad, I stop being sad and just be awesome instead.
(3+2n)/(3n+2) =quote:Op donderdag 17 januari 2013 02:15 schreef MouzurX het volgende:
Ik ben met reeksen en limieten bezig maar ik snap niet wat het antwoord op deze moet zijn:
limiet voor n naar oneindig (3+2^n)/(3^(n+2))
Ik pak het zo aan:
Eerst opsplitsen 3/(3^n*3^2) + 2^n/(3^n*3^2)
Dan de constanten naar voren: 3/9 * 1/3^n + 1/9 * 2^n/3^n
Dan machten naar boven: (1/3)^n + (2/3)^n.
Die zijn hetzelfde als 1/(1-x).
Dan kom je op: 3/9 * 3/2 + 1/9 * 3/1 = 5/6de uit.
Echter wolfram komt op 0 uit en een andere limieten bereken website op 4/9de.
Wat doe ik fout?
(3+2n)/(9*3n) = ... Remembert; an+2 = an*a2
3/(9*3n) + 2n/(9*3n) = ... hier breuk opsplitsen in 2 stukken
3/(32*3n) + 2n/(9*3n) =
3/(3n+2) + 2n/(9*3n) =
3/(3n+2) + 1/9 * 2n/*3n =
3/(3n+2) + 1/9 * (2/3)n = ... remembert; an/bn = (a/b)n
hiervan de limiet van x naar ∞ nemen
limx→∞ (3/(3n+2) + 1/9 * (2/3)n) =...
limx→∞3/(3n+2) + limx→∞ 1/9 * (2/3)n = 0 + 0
want de limiet voor x naar ∞ van 1/an voor elke a>1 is 0; evenzo voor bn voor 0 < b < 1.
[ Bericht 0% gewijzigd door VanishedEntity op 17-01-2013 04:25:53 ]
Nee ...quote:
Ik ben met reeksen en limieten bezig maar ik snap niet wat het antwoord op deze moet zijn:
limiet voor n naar oneindig van (3+2^n)/(3^(n+2))
Ik pak het zo aan:
Eerst opsplitsen 3/(3^n*3^2) + 2^n/(3^n*3^2)
Dan de constanten naar voren: 3/9 * 1/3^n + 1/9 * 2^n/3^n
Dan machten naar boven: (1/3)^n + (2/3)^n.
Die zijn hetzelfde als 1/(1-x).
Wat je fout doet is dat je rijen en reeksen met elkaar verwart. Je hebt een rij {an} gedefinieerd door:quote:Dan kom je op: 3/9 * 3/2 + 1/9 * 3/1 = 5/6 uit.
Echter wolfram komt op 0 uit en een andere limieten bereken website op 4/9.
Wat doe ik fout?
an = (3+2n)/3n+2
Nu wordt je gevraagd te berekenen:
limn→∞ an
Maar jij berekent in plaats daarvan:
limn→∞ ∑k=0n ak
Sorry ik heb het verkeerd gezegd de opdracht is:quote:
[..]
Nee ...
[..]
Wat je fout doet is dat je rijen en reeksen met elkaar verwart. Je hebt een rij {an} gedefinieerd door:
an = (3+2n)/3n+2
Nu wordt je gevraagd te berekenen:
limn→∞ an
Maar jij berekent in plaats daarvan:
limn→∞ ∑k=0n ak
When I get sad, I stop being sad and just be awesome instead.
Ah kijk, dan had je beter meteen de oorspronkelijke opgave kunnen posten. Een series is een reeks en dan heb je inderdaad een convergente reeks, aangezien de termen van deze reeks - zoals je zelf ook al had gevonden - bestaan uit een som van termen van twee convergente meetkundige reeksen met als reden resp. 1/3 en 2/3. En jazeker, Wolfram komt dan ook op 5/6 uit, kijk maar.quote:
[..]
Sorry ik heb het verkeerd gezegd de opdracht is:
[ afbeelding ]
[ Bericht 0% gewijzigd door Riparius op 17-01-2013 16:39:58 ]
Bedankt, maar nu snap ik het verschil niet tussen bovenstaande opgave en:quote:
[..]
Ah kijk, dan had je beter meteen de oorspronkelijke opgave kunnen posten. Een series is een reeks en dan heb je inderdaad een convergente reeks, aangezien de termen van deze reeks - zoals je zelf ook al had gevonden - bestaan uit de som van de termen van twee convergente meetkundige reeksen met als reden resp. 1/3 en 2/3. En jazeker, Wolfram komt dan ook op 5/6 uit, kijk maar.
Sum n->infinity (4+2^n)/(3^(n+2)) waar wolfram op 4/9de uitkomt( http://www.wolframalpha.c(...)%29%29+n-%3Einfinite)
En ik kan wel op 4/9de uitkomen maar dan moet ik een andere stap erbij doen:
4/(3^n+2) -> 4/9 * 1/3^n -> 4/9 * ( 1/(1-1/3) -1) = 2/9
2^n/3^(n+2) -> 1/9 * (2/3)^n -> 1/9 * (1/(1-1/3)-1) = 2/9 2/9+2/9 = 4/9
En mijn docent heeft het wel uitgelegd want die 1 komt dan van het begin van de reeks (1 + x + x^2 + x^3 etc) maar waarom je die hier er af moet trekken en bij de andere opgave niet?
When I get sad, I stop being sad and just be awesome instead.
Je bent een beetje aan het goochelen omdat je kennelijk niet goed snapt hoe je een convergente meetkundige reeks sommeert. En het maakt toch verschil of we beginnen bij n = 1 of bij n = 0, dat zie je toch wel?quote:
[..]
Bedankt, maar nu snap ik het verschil niet tussen bovenstaande opgave en:
Sum n->infinity (4+2^n)/(3^(n+2)) waar wolfram op 4/9de uitkomt( http://www.wolframalpha.c(...)%29%29+n-%3Einfinite)
En ik kan wel op 4/9de uitkomen maar dan moet ik een andere stap erbij doen:
4/(3^n+2) -> 4/9 * 1/3^n -> 4/9 * ( 1/(1-1/3) -1) = 2/9
2^n/3^(n+2) -> 1/9 * (2/3)^n -> 1/9 * (1/(1-1/3)-1) = 2/9 2/9+2/9 = 4/9
En mijn docent heeft het wel uitgelegd want die 1 komt dan van het begin van de reeks (1 + x + x^2 + x^3 etc) maar waarom je die hier er af moet trekken en bij de andere opgave niet?
[ Bericht 0% gewijzigd door Riparius op 18-01-2013 17:02:57 ]
Het duurde even maar ik zie dat ik bij wolfram inderdaad een fout heb gemaakt. Oke nu snap ik het. Heel erg bedankt.quote:
[..]
Je bent een beetje aan het googelen omdat je kennelijk niet goed snapt hoe je een convergente meetkundige reeks sommeert. En het maakt toch verschil of we beginnen bij n = 1 of bij n = 0, dat zie je toch wel?
When I get sad, I stop being sad and just be awesome instead.
Je kunt bij Wolfram gewoon opgeven bij welke waarde van n je wil beginnen als je een (convergente) oneindige reeks sommeert. Als je bijvoorbeeld wil beginnen bij n = 2 doe je dit.quote:Op donderdag 17 januari 2013 16:52 schreef MouzurX het volgende:
[..]
Het duurde even maar ik zie dat ik bij wolfram inderdaad een fout heb gemaakt. Oke nu snap ik het. Heel erg bedankt.
1. 2600 =1000/(kev – 0,10)
2. kev = 1300/2600 x 100%
Kan iemand mij uitleggen hoe ze van 1 naar 2 gaan?
2. kev = 1300/2600 x 100%
Kan iemand mij uitleggen hoe ze van 1 naar 2 gaan?
1.5. 2600(kev-0.10) = 1000
1300 moet 1260 zijn.
1300 moet 1260 zijn.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nee, want deze stap klopt niet. Vermenigvuldig in (1) eens beide leden met (kev - 0,10).quote:
1. 2600 =1000/(kev – 0,10)
2. kev = 1300/2600 x 100%
Kan iemand mij uitleggen hoe ze van 1 naar 2 gaan?
Ik snap nog steeds niet. Het antwoord is 10,038%quote:
1.5. 2600(kev-0.10) = 1000
1300 moet 1260 zijn.
Of het nou 1300 of 1260 is je komt nog steeds niet aan het juiste antwoord
1. 2600 =1000/(kev – 0,10)quote:
[..]
Nee, want deze stap klopt niet. Vermenigvuldig in (1) eens beide leden met (kev - 0,10).
2. 2600*(kev – 0,10) =1000
3. 2600kev-260 = 1000
4. 2600kev = 740
5. 3,5
wat doe ik hier verkeerrd?
Hier gaat het fout. Als je in (3) 260 optelt bij het linkerlid, dan moet je dat in het rechterlid ook doen, en er dus rechts niet 260 van aftrekken. Dan krijg je:quote:
[..]
1. 2600 = 1000/(kev – 0,10)
2. 2600∙(kev – 0,10) = 1000
3. 2600∙kev – 260 = 1000
4. 2600∙kev = 740
(4) 2600∙kev = 1260
OK! dat was een slordige fout van mij. Maar ik snap nog steeds niet hoe zij aan 10,038% als antwoord komen. Heb jij enig idee?quote:
[..]
Hier gaat het fout. Als je in (3) 260 optelt bij het linkerlid, dan moet je dat in het rechterlid ook doen, en er dus rechts niet 260 van aftrekken. Dan krijg je:
(4) 2600∙kev = 1260
Jazeker. Je hebt óf de opgave verkeerd overgenomen, óf er staat een typo in je boek. Maak de opgave nog maar eens overnieuw, maar begin nu met:quote:
[..]
OK! dat was een slordige fout van mij. Maar ik snap nog steeds niet hoe zij aan 10,038% als antwoord komen. Heb jij enig idee?
2600000 = 1000/(kev – 0,10)
[ Bericht 0% gewijzigd door Riparius op 17-01-2013 18:27:52 ]
Ja, maar ik ben net terug op de basis. Ik heb heel wat op- en aanmerkingen, en ik zal vanavond een begin maken met die op te schrijven.quote:Op donderdag 17 januari 2013 18:20 schreef Amoeba het volgende:
[..]
Heb jij trouwens die PDF al ingekeken?
Verdammt. is het nog goed als ik een aangepaste versie adhv mijn gesprek met dhr wiskundedocent stuur?quote:
[..]
Ja, maar ik ben net terug op de basis. Ik heb heel wat op- en aanmerkingen, en ik zal vanavond een begin maken met die op te schrijven.
Als je die nu beschikbaar hebt, dan vind ik dat prima.quote:
[..]
Verdammt. is het nog goed als ik een aangepaste versie adhv mijn gesprek met dhr wiskundedocent stuur?
260000 = 1000/(kev – 0,10)quote:
[..]
Jazeker. Je hebt óf de opgave verkeerd overgenomen, óf er staat een typo in je boek. Maak de opgave nog maar eens overnieuw, maar begin nu met:
260000 = 1000/(kev – 0,10)
260000*(kev – 0,10) = 1000
260000*kev –26000 = 1000
260000*kev = 27000
10,83
Zo klopt ie wel en en ik heb zeker weten goed overgenomen uit antwoordmodel,
I
Binnen een kwartiertje heb je 'mquote:
[..]
Als je die nu beschikbaar hebt, dan vind ik dat prima.
Ik had helaas zelf nog een nul te weinig toegevoegd. Zie correctie hierboven. Dan kom je inderdaad op 10,038 % uit.quote:
[..]
260000 = 1000/(kev – 0,10)
260000*(kev – 0,10) = 1000
260000*kev –26000 = 1000
260000*kev = 27000
10,38
Zo klopt ie wel en en ik heb zeker weten goed overgenomen uit antwoordmodel,
I
Riparius kan jij mij uitleggen hoe je Ke kan berekenen:
MPAo= D1/(Ke-g)
MPAo*(Ke-g)=D1
MPAo=D1/(Ke-g)
MPAo=D1/Ke-D1/G
Hoe zet ik Ke voor de =-teken?
MPAo= D1/(Ke-g)
MPAo*(Ke-g)=D1
MPAo=D1/(Ke-g)
MPAo=D1/Ke-D1/G
Hoe zet ik Ke voor de =-teken?
Ok, bedankt, je hebt een scherp oog voor detail.quote:
[..]
Ik had helaas zelf nog een nul te weinig toegevoegd. Zie correctie hierboven. Dan kom je inderdaad op 10,038 % uit.
Je derde regel is identiek met je eerste, dus zo schiet het niet op. Eerst beide leden vermenigvuldigen met (Ke - g), dat geeft:quote:
Riparius kan jij mij uitleggen hoe je Ke kan berekenen:
MPAo= D1/(Ke-g)
MPAo*(Ke-g)=D1
MPAo=D1/(Ke-g)
MPAo*(Ke - g) = D1
Nu haakjes wegwerken in het linkerlid. We hebben a(b-c) = ab - ac en dus krijgen we hier:
MPAo*Ke - MPAo*g = D1
Nu wil je alle termen met Ke in het linkerlid hebben/houden, en alle termen zonder Ke in het rechterlid. Dus gaan we hier MPAo*g optellen bij beide leden. Dit geeft:
MPAo*Ke = D1 + MPAo*g
Nu nog beide leden delen door MPAo en we krijgen:
Ke = (D1 + MPAo*g)/MPAo
Dit kun je ook nog schrijven als:
Ke = g + D1/MPAo
Kun je een keer uitleggen waar je mee bezig bent? Je werkt met de meest idiote variabelen voor mijn oog terwijl je (inhoudelijk gezien) met de basis van wiskunde bezig bent.quote:
Riparius kan jij mij uitleggen hoe je Ke kan berekenen:
MPAo= D1/(Ke-g)
MPAo*(Ke-g)=D1
MPAo=D1/(Ke-g)
MPAo=D1/Ke-D1/G
Hoe zet ik Ke voor de =-teken?
[ Bericht 1% gewijzigd door #ANONIEM op 17-01-2013 18:52:49 ]
Zou je volgende keer AUB enkelletterige variabelen (evt met subscript indices) voor je formules willen gebruiken alstjebliefdankjewelgraaggedaan? Zo is er nl. geen beginnen aan...quote:
Riparius kan jij mij uitleggen hoe je Ke kan berekenen:
MPAo= D1/(Ke-g)
MPAo*(Ke-g)=D1
MPAo=D1/(Ke-g)
MPAo=D1/Ke-D1/G
Hoe zet ik Ke voor de =-teken?
Dat blijkt. Het oogt, zacht uitgedrukt, ontzettend onoverzichtelijk en non wiskundig.quote:
Volgens mij zijn economen dol op formules met woorden en afkortingen erin. Dan krijg je dat.
Ik heb geen idee wat je uberhaupt doet (misschien haakjes vergeten bij de (5+m) ?). Anders zou eens beginnen met het vermenigvuldigen van beide leden met m, en gebruiken dat 175/5=35, zodat je krijgt
20 = 35m + m²
20 = 35m + m²
20/m = 175/(5+m)quote:
Ja, de haakjes was ik vergeten
20/m = 175/(5+m)
Ik doe
20*5+20*m =175*m
100+20m = 175m
Beide leden keer 5+m:
20(5+m)/m = 175
(100+20m)/m = 175
100/m + 20 = 175
Dus 100 + 20m = 175m.
Klopt?
