SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
stel x=a en sqrt(x) = bquote:Op dinsdag 16 oktober 2012 22:35 schreef OhNoes het volgende:
even een klein vraagje; (x*sqrtx)² = x² * x V x * x?
(ab)^2=a^2b^2=x^2(sqrtx)^2=x^2*x=x^3
Weet alleen niet zeker of dit de "wortel opheft", of dat deze dan alleen bestaat voor positieve x.
Oke, weer wat geleerd :]quote:Op dinsdag 16 oktober 2012 22:36 schreef GlowMouse het volgende:
[..]
De V is wat anders als het woordje 'en', aan beide kanten van de V moeten situaties staan, dus je bedoelt:
(x*sqrtx)² = x² * x V (x*sqrtx)² = x * x
en dat is een ware uitspraak.
Maar de vraag was eigenlijk of de uitkomst x² * x was, of dat de uitkomst x * x was?
Ik denk x² * x
² betekent keer zichzelf, dus (x*sqrtx)² = (x*sqrtx)*(x*sqrtx)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik snap trouwens niet hoe ik te werk moet gaan bij het integreren van een "normale" goniometrische functie en een hyperbolische, dwz functies van het type sin(x)sinh(x), cos(x)/cosh(x) etc. Apart lukt wel maar juist bij vermenigvuldigen/delen etc. zou ik eigenlijk niet weten waar te beginnen.
Pas de rekenregel (a∙b)p = ap∙bp toe.quote:
[..]
Oke, weer wat geleerd :]
Maar de vraag was eigenlijk of de uitkomst x² * x was, of dat de uitkomst x * x was?
Ik denk x² * x
Om sin(x)∙sinh(x) te primitiveren kun je gebruik maken van de regel voor partieel integreren. Dit is de tegenhanger van de productregel bij het differentiëren. De afgeleide van u(x)∙v(x) naar x is u'(x)∙v(x) + u(x)∙v'(x), en dus hebben we ook:quote:
Ik snap trouwens niet hoe ik te werk moet gaan bij het integreren van een "normale" goniometrische functie en een hyperbolische, dwz functies van het type sin(x)sinh(x), cos(x)/cosh(x) etc. Apart lukt wel maar juist bij vermenigvuldigen/delen etc. zou ik eigenlijk niet weten waar te beginnen.
Aangezien du = u'(x)⋅dx en dv = v'(x)⋅dx kun je dit compacter opschrijven als:
Zie ook hier. Probeer nu zelf eens ∫ sin(x)∙sinh(x)⋅dx te bepalen met behulp van deze regel. Hint: je moet de regel tweemaal toepassen. Een primitieve van cos(x)/cosh(x) is overigens niet in elementaire functies uit te drukken.
[ Bericht 0% gewijzigd door Riparius op 17-10-2012 02:01:51 ]
Weet iemand nog een leuk onderwerp of gebied voor een bachelorscriptie?
Ik kan ook andere vakken kiezen zodat ik geen scriptie hoef te maken, maar het lijkt me eigenlijk wel leuk.
Ik ben wel een beetje bang dat ik met mijn scriptie niet echt wat zal kunnen 'toevoegen'. Het is ook toegestaan een samenvattende scriptie te schrijven, maar dat lijkt me toch net wat minder. Iemand ideeën of nog leuker, wie heeft er al een (bachelor)scriptie gedaan en waarover?
Ik kan ook andere vakken kiezen zodat ik geen scriptie hoef te maken, maar het lijkt me eigenlijk wel leuk.
Ik ben wel een beetje bang dat ik met mijn scriptie niet echt wat zal kunnen 'toevoegen'. Het is ook toegestaan een samenvattende scriptie te schrijven, maar dat lijkt me toch net wat minder. Iemand ideeën of nog leuker, wie heeft er al een (bachelor)scriptie gedaan en waarover?
Ik was zelf ook niet voor een theoretische bsc-scriptie gegaan, want dan wordt het meestal toch niet veel meer dan een uitgebreid literatuuronderzoek. Alhoewel dat er ook wel voor kan zorgen dat je leert waar wel/niet je interesses liggen, buiten de standaard vakken.
Als ik jou was zou ik het denk ik zoeken in de richting van algoritmes die je ergens op kan toepassen, zeker als je ook informatica studeert. En dan misschien verschillende algoritmes schrijven en performance vergelijken. Er is dan meestal ook wel ruimte om zelf met je algoritmes te klooien om het te verbeteren. Er zit toch een stuk theorie achter, maar je bent ook wel echt zelf bezig.
Als ik jou was zou ik het denk ik zoeken in de richting van algoritmes die je ergens op kan toepassen, zeker als je ook informatica studeert. En dan misschien verschillende algoritmes schrijven en performance vergelijken. Er is dan meestal ook wel ruimte om zelf met je algoritmes te klooien om het te verbeteren. Er zit toch een stuk theorie achter, maar je bent ook wel echt zelf bezig.
Thanks! Dat wist ik niet zo meer, uit mijn hoofd.quote:
tan(a+b) = (tan(a)+tan(b))/(1-tan(a)tan(b))
Je moet trouwens tan(α - β) = (tan α - tan β)/(1 + tan α∙tan β) gebruiken. Zie mijn PDF over goniometrische identiteiten. En schrijf 54° om aan te geven dat je in graden werkt, of schrijf in plaats daarvan (3/10)∙π.quote:Op donderdag 18 oktober 2012 16:40 schreef Dale. het volgende:
[..]
Thanks! Dat wist ik niet zo meer, uit mijn hoofd.
I know maar kon het ° niet zo snel vinden in speciale tekens. En dacht toch wel dat 54 graden duidelijk wasquote:
[..]
Je moet trouwens tan(α - β) = (tan α - tan β)/(1 + tan α∙tan β) gebruiken. Zie mijn PDF over goniometrische identiteiten. En schrijf 54° om aan te geven dat je in graden werkt, of schrijf in plaats daarvan (3/10)∙π.
. En het eerste wist ik ook :-)
°
Je kunt (bij de in Nederland standaard gebruikte toetsenbordindeling VS internationaal) een ° typen door de rechter Alt toets en de Shift toets ingedrukt te houden en dan : te typen (op de toets waar ook ; zit). Het was inderdaad wel duidelijk dat het graden moesten zijn want een arcus tangens ligt altijd tussen -½π en +½π (rad) oftewel -90° en +90°.quote:
[..]
I know maar kon het ° niet zo snel vinden in speciale tekens. En dacht toch wel dat 54 graden duidelijk was
tof, nu weet ik ook hoe ik ¬________¬ moet typen
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Posters die geen gebruik willen maken van TeX en ook geen speciale (unicode) toetsenbord layouts (met WYSIWYG) willen gebruiken en ook geen moeilijk te onthouden codes willen gebruiken voor speciale tekens kan ik aanraden eens naar HTML 4.0 Entities te kijken (link). Zo typ je ook heel gemakkelijk een ° als & deg; of een ¬ als & not; (geen spatie gebruiken na de ampersand). Ook Griekse letters en de meeste courante wiskundige symbolen gaan dan heel gemakkelijk, bijvoorbeeld & ang; voor ∠ of & radic; voor √.
⇒
∩
∪
⊂
⋅
≤
Netjes. Wel handig als je één symbooltje als ≤ wil en dan niet direct die tex-tags hoeft te typen.
∩
∪
⊂
⋅
≤
Netjes. Wel handig als je één symbooltje als ≤ wil en dan niet direct die tex-tags hoeft te typen.
Dat is inderdaad wel een goed idee, ik zag bij een paar andere bachelorscripties inderdaad ook dat idee (en dat ze inderdaad ook echt een algoritme konden verbeteren, qua looptijd). Goed onthouden trouwens dat ik ook informatica doequote:
Ik was zelf ook niet voor een theoretische bsc-scriptie gegaan, want dan wordt het meestal toch niet veel meer dan een uitgebreid literatuuronderzoek. Alhoewel dat er ook wel voor kan zorgen dat je leert waar wel/niet je interesses liggen, buiten de standaard vakken.
Als ik jou was zou ik het denk ik zoeken in de richting van algoritmes die je ergens op kan toepassen, zeker als je ook informatica studeert. En dan misschien verschillende algoritmes schrijven en performance vergelijken. Er is dan meestal ook wel ruimte om zelf met je algoritmes te klooien om het te verbeteren. Er zit toch een stuk theorie achter, maar je bent ook wel echt zelf bezig.
.
Ken je het proof-number search algoritme? Dat is een algoritme om zero-sum spellen met volledige informatie op te lossen. Oplossen als in: volledig doorrekenen, dus bij schaken werkt het niet zo goed, maar andere spellen zoals vier-op-een-rij wel. Er zijn allerlei uitbreidingen en tweaks met dat algoritme mogelijk. Volgens mij valt daar zeker wat interessants mee te doen.
Omdat de tree dan te groot wordt bedoel je?quote:
dus bij schaken werkt het niet zo goed
Dat, en omdat er te weinig geforceerde varianten in zitten.quote:
[..]
Omdat de tree dan te groot wordt bedoel je?
Ken ik niet nee. Toevallig ben ik nu wel bezig met een practicum waarbij je moet uitzoeken of er een winnende tactiek mogelijk is bij het schaken (dus ik weet niet, het zal wel een ander algoritme zijn, ik heb er nog niet echt naar gekeken).quote:
Ken je het proof-number search algoritme? Dat is een algoritme om zero-sum spellen met volledige informatie op te lossen. Oplossen als in: volledig doorrekenen, dus bij schaken werkt het niet zo goed, maar andere spellen zoals vier-op-een-rij wel. Er zijn allerlei uitbreidingen en tweaks met dat algoritme mogelijk. Volgens mij valt daar zeker wat interessants mee te doen.
Ik zal er binnenkort eens naar kijken, ik vind dat soort dingen altijd wel interessant
Dank! (ook thenxzero!)
Waarom zijn submartingales gedefinieerd als een stochastisch proces met een stijgende trend? Bij sub denk ik aan "laag" of "onder". Dus ik zou verwachten dat submartingales een dalende trend zouden hebben.
Ik heb dit nooit begrepen. Zit hier een bepaalde logica achter?
Ik heb dit nooit begrepen. Zit hier een bepaalde logica achter?
Iemand die mij kan helpen met de volgende vragen:
http://i.imgur.com/BdvQ4.jpg
Vraag 4, 5 en 6. Ik heb geen idee waar ik moet beginnen.
http://i.imgur.com/BdvQ4.jpg
Vraag 4, 5 en 6. Ik heb geen idee waar ik moet beginnen.
keesjeislief zit volgens mij in de martingalesquote:
Waarom zijn submartingales gedefinieerd als een stochastisch proces met een stijgende trend? Bij sub denk ik aan "laag" of "onder". Dus ik zou verwachten dat submartingales een dalende trend zouden hebben.
Ik heb dit nooit begrepen. Zit hier een bepaalde logica achter?
ik zal je wat zoekwoorden geven:quote:
Iemand die mij kan helpen met de volgende vragen:
http://i.imgur.com/BdvQ4.jpg
Vraag 4, 5 en 6. Ik heb geen idee waar ik moet beginnen.
4: lineaire benadering
5: kettingregel
6: als je hem niet direct ziet, probeer dan te vereenvoudigen
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
quote:
Iemand die mij kan helpen met de volgende vragen: http://i.imgur.com/BdvQ4.jpg
Vraag 4, 5 en 6. Ik heb geen idee waar ik moet beginnen.
nog meer hints:quote:
ik zal je wat zoekwoorden geven:
4: lineaire benadering
5: kettingregel
6: als je hem niet direct ziet, probeer dan te vereenvoudigen
4. kettingregel, maar dan in dit geval dy/dx = dy/du * du/dv * dv/dx
5. eerst x en y in termen van t uitdrukken, dan direct in de exponent inpluggen.
6. Ik zie hier geen variabele staan
.
Laat eerst eens zien wat je eigen gedachten zijn over deze opgaven. Het is wat te gemakkelijk om bij dit soort opgaven te zeggen dat je geen idee hebt waar te beginnen, dat is alleen maar een excuus om niets te proberen. Deze drie opgaven hebben trouwens wel gemeen dat je eerst de gegeven uitdrukkingen kunt vereenvoudigen alvorens er verder mee te gaan rekenen. De opstellers van deze vragen willen zo kennelijk het kaf van het koren kunnen scheiden ...quote:
Iemand die mij kan helpen met de volgende vragen:
http://i.imgur.com/BdvQ4.jpg
Vraag 4, 5 en 6. Ik heb geen idee waar ik moet beginnen.
Ik heb het volgende bewijs dat de som van twee poisson processen een poisson process is.
Ik vroeg mij af of dit niet op één of andere manier veel makkelijker te bewijzen is? Iemand een idee?
Ik vroeg mij af of dit niet op één of andere manier veel makkelijker te bewijzen is? Iemand een idee?
Met kansgenererende functies of het volgende doen:quote:
Ik heb het volgende bewijs dat de som van twee poisson processen een poisson process is.
[ afbeelding ]
Ik vroeg mij af of dit niet op één of andere manier veel makkelijker te bewijzen is? Iemand een idee?
Zeg dat Y = X1 + X2 waarbij X1 en X2 poisson processen zijn met verschillende parameters.
Vervolgens kun je P(Y=k) als volgt bepalen:
Als je dit uitwerkt zul je zien dat Y inderdaad een poisson proces is.
Een poissonproces heeft wel wat meer eigenschappen dan je nu checkt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Door t=0 in te vullen in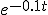 
.
The biggest argument against democracy is a five minute discussion with the average voter.
Voor mijn gevoel is mijn probleem vrij simpel maar ik krijg er de vinger niet achter. Hierbij een fictief voorbeeld.
Ik heb 3 flessen met water. In de ene zit 1 liter, in tweede zit 2 liter en in de derde 3 liter.
De flessen hangen onderste boven en er zit een slangetje in waardoor 0,025 liter per minuut kan stromen.
De slangetjes van 2 en 3 komen samen in slangetje 4 waardoor ook 0,025 liter water per minuut kan stromen
Slangetje 1 en 4 komen samen in slangetje 5 waardoor ook 0,025 liter water per minuut kan stromen.
Slangetje 5 komt uit in een bak waar de flessen in leeglopen.
Hoe kan ik de inhoud van de flessen op elk tijdstip t bepalen?
Zodra fles 1 leeg is, kunnen 2 en 3 sneller leegstromen, hoe verwerk ik die omslagpunten in een algemene formule?
Ik kan het wel simpelweg uitrekenen, maar ik heb ook complexere situaties.
Ik hoop dat iemand me kan helpen of aan kan geven dat er niet zo'n formule is.
Ik heb 3 flessen met water. In de ene zit 1 liter, in tweede zit 2 liter en in de derde 3 liter.
De flessen hangen onderste boven en er zit een slangetje in waardoor 0,025 liter per minuut kan stromen.
De slangetjes van 2 en 3 komen samen in slangetje 4 waardoor ook 0,025 liter water per minuut kan stromen
Slangetje 1 en 4 komen samen in slangetje 5 waardoor ook 0,025 liter water per minuut kan stromen.
Slangetje 5 komt uit in een bak waar de flessen in leeglopen.
Hoe kan ik de inhoud van de flessen op elk tijdstip t bepalen?
Zodra fles 1 leeg is, kunnen 2 en 3 sneller leegstromen, hoe verwerk ik die omslagpunten in een algemene formule?
Ik kan het wel simpelweg uitrekenen, maar ik heb ook complexere situaties.
Ik hoop dat iemand me kan helpen of aan kan geven dat er niet zo'n formule is.
Wie bang is voor morgen, kan niet genieten van vandaag.
Religie is als taal, een basisbehoefte voor een maatschappij, iedereen spreekt zijn eigen dialect en even verder op begrijp je niet meer wat de ander zegt.
Religie is als taal, een basisbehoefte voor een maatschappij, iedereen spreekt zijn eigen dialect en even verder op begrijp je niet meer wat de ander zegt.
Je vraagstuk is niet op te lossen zonder bepaalde additionele aannames, waar je niets over zegt. Je zegt bijvoorbeeld niet of je aanneemt dat de flessen lineair met de tijd leeglopen. In werkelijkheid zal dat niet zo zijn, maar het is niet duidelijk of je daar wel van uit gaat. En waarom doe je zo geheimzinnig door het vraagstuk te presenteren als een 'fictief' voorbeeld? Daarmee suggereer je dat je in werkelijkheid een heel ander vraagstuk wil oplossen. Dan kun je beter iets over dat andere vraagstuk vertellen.quote:
Voor mijn gevoel is mijn probleem vrij simpel maar ik krijg er de vinger niet achter. Hierbij een fictief voorbeeld.
Ik heb 3 flessen met water. In de ene zit 1 liter, in tweede zit 2 liter en in de derde 3 liter.
De flessen hangen onderste boven en er zit een slangetje in waardoor 0,025 liter per minuut kan stromen.
De slangetjes van 2 en 3 komen samen in slangetje 4 waardoor ook 0,025 liter water per minuut kan stromen
Slangetje 1 en 4 komen samen in slangetje 5 waardoor ook 0,025 liter water per minuut kan stromen.
Slangetje 5 komt uit in een bak waar de flessen in leeglopen.
Hoe kan ik de inhoud van de flessen op elk tijdstip t bepalen?
Zodra fles 1 leeg is, kunnen 2 en 3 sneller leegstromen, hoe verwerk ik die omslagpunten in een algemene formule?
Ik kan het wel simpelweg uitrekenen, maar ik heb ook complexere situaties.
Ik hoop dat iemand me kan helpen of aan kan geven dat er niet zo'n formule is.
Het is ook onmogelijk om met een "algmene" formule te komen, als je niet specificeert in wat voor algemeenheid je dit soort problemen wilt oplossen.
Het is inderdaad een ander vraagstuk, wat op zich zelf ook fictief is maar heel veel randvoorwaarden in zitten. Ik had het probleem voor me zelf versimpelt met de flessen. Ik denk dat ik anders nodeloos ingewikkeld maak.quote:
[..]
Je vraagstuk is niet op te lossen zonder bepaalde additionele aannames, waar je niets over zegt. Je zegt bijvoorbeeld niet of je aanneemt dat de flessen lineair met de tijd leeglopen. In werkelijkheid zal dat niet zo zijn, maar het is niet duidelijk of je daar wel van uit gaat. En waarom doe je zo geheimzinnig door het vraagstuk te presenteren als een 'fictief' voorbeeld? Daarmee suggereer je dat je in werkelijkheid een heel ander vraagstuk wil oplossen. Dan kun je beter iets over dat andere vraagstuk vertellen.
Het gaat me dan ook om het wiskundige kernprincipe van de flessen, wat ik graag wil begrijpen. De snelheid van leeglopen gaat met een constante snelheid, de slangetjes zijn bij wijze van spreke even lang en hebben geen weerstand en de boel wordt netjes evenredig verdeeld over de slangetjes.
Dus na 120 minuten is fles 1 leeg en zit in fles 2 nog 1 liter en in fles 3 nog 2 liter.
Na 200 minuten is fles 2 leeg en zit in fles 3 nog 1 liter.
Na 240 minuten zijn alle flessen leeg.
Is dit genoeg info?
[ Bericht 0% gewijzigd door iamcj op 26-10-2012 21:20:02 ]
Wie bang is voor morgen, kan niet genieten van vandaag.
Religie is als taal, een basisbehoefte voor een maatschappij, iedereen spreekt zijn eigen dialect en even verder op begrijp je niet meer wat de ander zegt.
Religie is als taal, een basisbehoefte voor een maatschappij, iedereen spreekt zijn eigen dialect en even verder op begrijp je niet meer wat de ander zegt.
Ik wil graag op ieder tijdstip t de inhoud van alle 3 de flessen afzonderlijk kunnen bepalen.quote:
Naar wat voor formule ben je op zoek?
Dat zijn denk 3 aparte formules op basis van 1 vergelijking.
Wie bang is voor morgen, kan niet genieten van vandaag.
Religie is als taal, een basisbehoefte voor een maatschappij, iedereen spreekt zijn eigen dialect en even verder op begrijp je niet meer wat de ander zegt.
Religie is als taal, een basisbehoefte voor een maatschappij, iedereen spreekt zijn eigen dialect en even verder op begrijp je niet meer wat de ander zegt.
Ja je krijgt minstens drie formules. Je kan het op allerlei manieren opschrijven.
Je kan bijvoorbeeld zeggen de ene formule voor een bepaalde fles is geldig op een bepaald tijdsinterval (waar de uitstroomsnelheid gelijk blijft), en na dat interval krijg je een andere formule, etc... En dat voor alle flessen.
Maar omdat je doel nogal vaag is weet ik niet of dit helpt.
Je kan bijvoorbeeld zeggen de ene formule voor een bepaalde fles is geldig op een bepaald tijdsinterval (waar de uitstroomsnelheid gelijk blijft), en na dat interval krijg je een andere formule, etc... En dat voor alle flessen.
Maar omdat je doel nogal vaag is weet ik niet of dit helpt.
Zover was ik zelf ook, maar als fles 1 leeg is, moet die term als het ware 0 worden.quote:
Ja je krijgt minstens drie formules. Je kan het op allerlei manieren opschrijven.
Je kan bijvoorbeeld zeggen de ene formule voor een bepaalde fles is geldig op een bepaald tijdsinterval (waar de uitstroomsnelheid gelijk blijft), en na dat interval krijg je een andere formule, etc... En dat voor alle flessen.
Maar omdat je doel nogal vaag is weet ik niet of dit helpt.
Ik zelf zat de denken richting differentiëren, maar daar houdt mijn wiskundige kennis op.
Wie bang is voor morgen, kan niet genieten van vandaag.
Religie is als taal, een basisbehoefte voor een maatschappij, iedereen spreekt zijn eigen dialect en even verder op begrijp je niet meer wat de ander zegt.
Religie is als taal, een basisbehoefte voor een maatschappij, iedereen spreekt zijn eigen dialect en even verder op begrijp je niet meer wat de ander zegt.
Misschien ben je op zoek naar een notatie als
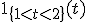
Die functie is 1 in het tijdsinterval tussen 1 en 2 en anders 0.
Daarmee kan je voor iedere fles 1 vergelijking opschrijven. Maar een algemene formule zou ik het niet noemen, want als je andere flessen en buisjes krijgt kan je weer opnieuw beginnen.
En differentiëren van lineaire functies is niet bijster interessant, dan krijg je gewoon de richtingscoëfficiënt...
Die functie is 1 in het tijdsinterval tussen 1 en 2 en anders 0.
Daarmee kan je voor iedere fles 1 vergelijking opschrijven. Maar een algemene formule zou ik het niet noemen, want als je andere flessen en buisjes krijgt kan je weer opnieuw beginnen.
En differentiëren van lineaire functies is niet bijster interessant, dan krijg je gewoon de richtingscoëfficiënt...
Wat ik zou willen is
t = tijd
s = druppelsnelheid
x = verdeelde druppelsnelheid
t · s = (1- (tx1)) + (2 - (tx2)) + (3 - (tx3)
waarbij s = x1 + x2 + x3
En als de eerste term gelijk is aan 0, dat hij dat blijft, zodat s = 0 + x2 + x3
Voor mijn gevoel mis ik alleen de wiskundige techniek of truc om dit te realiseren.
[ Bericht 11% gewijzigd door iamcj op 26-10-2012 21:51:43 ]
t = tijd
s = druppelsnelheid
x = verdeelde druppelsnelheid
t · s = (1- (tx1)) + (2 - (tx2)) + (3 - (tx3)
waarbij s = x1 + x2 + x3
En als de eerste term gelijk is aan 0, dat hij dat blijft, zodat s = 0 + x2 + x3
Voor mijn gevoel mis ik alleen de wiskundige techniek of truc om dit te realiseren.
[ Bericht 11% gewijzigd door iamcj op 26-10-2012 21:51:43 ]
Wie bang is voor morgen, kan niet genieten van vandaag.
Religie is als taal, een basisbehoefte voor een maatschappij, iedereen spreekt zijn eigen dialect en even verder op begrijp je niet meer wat de ander zegt.
Religie is als taal, een basisbehoefte voor een maatschappij, iedereen spreekt zijn eigen dialect en even verder op begrijp je niet meer wat de ander zegt.
Je geeft zelf eigenlijk al de oplossing aan, en thenxero verduidelijkt dat door aan te geven dat je de tijd in een aantal deelintervallen op kunt delen. Dan is de hoeveelheid water in elk van de flessen binnen elk deelinterval een lineaire functie van de tijd. Jij lijkt op zoek te zijn naar een lineaire functie voor de hoeveelheid water in elke fles als functie van de tijd die geldig is op het gehele tijdsinterval, vanaf t = 0 totdat alle flessen leeg zijn, maar dat kan niet: de grafieken voor de hoeveelheid water in elke fles als functie van de tijd bestaan weliswaar uit rechte lijnstukken, maar vertonen 'knikken'.quote:
Voor mijn gevoel mis ik alleen de wiskundige techniek of truc om dit te realiseren.
[ Bericht 1% gewijzigd door Riparius op 28-10-2012 00:42:59 ]
quote:
[..]
Met kansgenererende functies of het volgende doen:
Zeg dat Y = X1 + X2 waarbij X1 en X2 poisson processen zijn met verschillende parameters.
Vervolgens kun je P(Y=k) als volgt bepalen:
Als je dit uitwerkt zul je zien dat Y inderdaad een poisson proces is.
Bedankt,quote:
Een poissonproces heeft wel wat meer eigenschappen dan je nu checkt.
De docent gaf nog de hint dat het met differentiëren heel makkelijk te bewijzen is. Ik heb al zitten googlen maar kan eigenlijk niks vinden.
